可透浪斜坡式防波堤透浪系数对入射波要素的响应

潘天娇，冯 曦，倪兴也，冯卫兵，马钢峰

(1.河海大学海岸灾害及防护教育部重点实验室，江苏 南京 210098；2.河海大学港口海岸与近海工程学院，江苏 南京 210098； 3.美国欧道明大学土木与环境工程系，Norfolk Virginia 23455)

斜坡式防波堤通常由堤心块石、护面块体等材料构成，其主要作用是阻挡外海波浪的传播，从而降低港内波高，保证港内水域平稳和正常作业。由于实体防波堤会限制港内外水体交换，影响近海生态环境，近年来可渗透防波堤在海岸工程中得到广泛应用。可渗透防波堤堤内块石孔隙较大，波浪容易透过堤身传至堤后，尤其在较长周期波浪区域。由于较长周期波浪穿透性强，且不易在堤后消减，影响了港内泊稳条件[1]，因此，需要对防波堤的透浪特性进行研究，通过合理设计，使之既能满足抗浪防灾的要求，又能兼顾对环境的最大保护。

波浪在穿透防波堤时，由于堤心石阻隔，消耗了部分能量并产生波能衰减。针对可渗透防波堤的特性，国内外学者开展了相关研究，认为波浪的穿透性与防波堤堤心石尺寸[2]、孔隙度[3]、堤身宽度[4-5]等物理特性，不同波浪类型、波高和周期[6-7]等波浪特性，以及物理模型试验比尺效应均相关。目前，多数研究旨在寻找堤心材料[8]或堤身结构本身与消浪系数之间的经验关系，少部分涉及透浪性能的内部机制探求，如孔隙压力与透浪特性之间联系[9-11]，由此也产生了一些不越浪斜坡式防波堤透浪系数的半经验半理论公式[2，6，12-16]。

然而，上述公式多建立在实验室规则波情境下，针对不规则波透浪性的研究较少；同时，多数研究关注堤坝内部结构对透浪系数的影响，却鲜有探讨波浪本身的特征要素对穿透力的影响；而后者则决定防波堤设计方案的适用性。本文结合物理模型与数值模拟试验，探讨不越浪-可透浪斜坡式防波堤的透浪特性对不同堤要素和波要素的响应，并比较了入射波分别为规则波与不规则波时透浪特性的不同，提出了更能反映真实情况的透浪系数表达式。

1 试验设备及布置

1.1 试验设备

物理模型试验在海岸灾害及防护教育部重点实验室(河海大学)的波浪水槽内进行。水槽有效长度80 m，宽1 m，高1.8 m，底面由光滑平整的混凝土砌筑而成，两侧为透明玻璃板。试验中，水槽被透明玻璃板隔成两半，即有效宽度为0.5 m。仅使用外侧进行试验断面铺设，内侧用于减小二次反射的影响。水槽前后端均设消能缓坡，以减小波浪反射。通过水槽一端的液压式推板造波机产生试验所需的规则波和不规则波。物理模型试验布置、模型精度、试验方法等均遵守JTJ/T 234—2001《波浪模型试验规程》，根据物理模型相似理论，按照重力相似原则设计模型。结合实验室水槽尺度、模型断面尺寸、水深、波要素等条件，采用正态模型几何比尺1∶30。

1.2 试验布置

斜坡式防波堤采用抛石结构，堤前迎浪面放置扭王字块体，护面块体不规则摆放，两侧坡度均为1∶1.5，堤身高度为84 cm，堤身宽度(静水面处)采用110 cm、140 cm和170 cm 3种，堤心石由中值粒径D50=0.017 m、孔隙率n=0. 45的不均匀块石组成。试验水深保持不变，d=40 cm。斜坡式防波堤前后共布置6根浪高仪，用于测定波浪沿程的衰减，在进行堤后波高分析时采用浪高仪c的数值。斜坡式防波堤试验图、模型布置见图1。

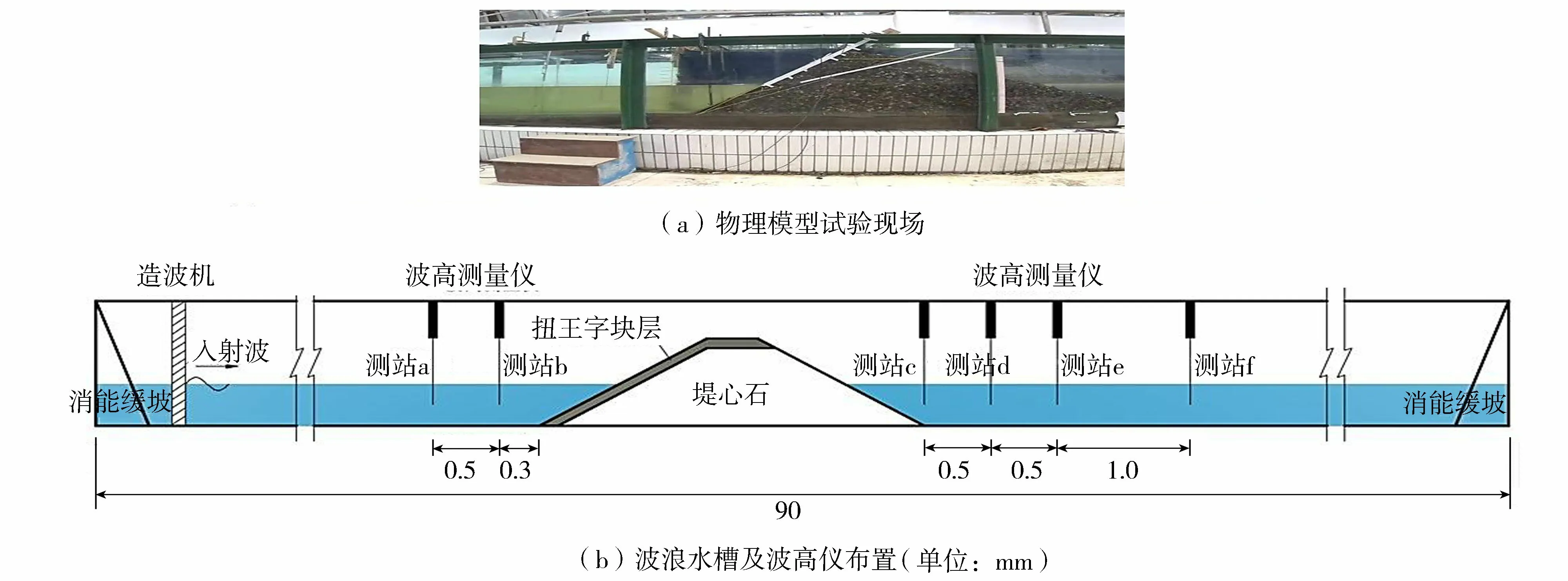
图1 斜坡式防波堤物理模型试验现场和波浪水槽及波高仪布置Fig.1 Site condition of physical model test and layouts of wave flume and wave gauges

1.3 波浪参数

入射波考虑规则波和不规则波(JONSWAP谱，谱峰高度因子3.3)两种情况，均按不越浪情形设计波浪入射条件。对每个模型样本，规则波试验采用间断造波法，以消除多次反射的影响。每组试验一次造波约20个，然后停机，待水面平静后再次造波，重复3次。不规则波每组试验时长250～300 s，停机待水面平静后再次造波，同样重复3次，均取平均值作为测量值[17]，总计试验组次为207组。采用DJ800型多功能监测系统进行波浪数据采集，该系统由计算机、多功能监测仪和各种传感器组成。采用上跨零点法，通过调节阀值消去由破碎和反射生成的波，规则波波高取10个波的平均波高H；不规则波特征波高取1/3大波的值，即有效波高Hs，所对应的波周期记为有效波周期Ts。不同组次波要素见表1。

表1 规则波与不规则波透浪物理模型试验设计波浪要素

2 数学模型及验证

2.1 模型控制方程

数值模拟采用非静压模型NHWAVE[18-19]，基于体积平均-雷诺平均-NS方程(VARANS)建立三维动压模型，可用于模拟动水压力、波浪作用下的自由表面运动等，并能较好地反映近海波浪的传播过程(包括浅水变形，反射，透射，破碎等)。该模型主要控制方程如下：

(1)

(2)

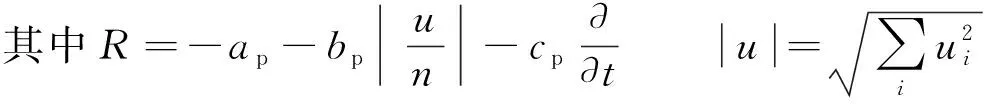
A=|u|/(nTg)K=|u|T/(nD50)

2.2 数值离散

NHWAVE采用有限差分格式和有限体积法结合的方式求解方程，采用间断捕捉HLL TVD法离散动量方程。在求解湍流模型(k-ε)方程组时，由HLPA法确定其对流项，该方法在空间上达二阶精度。为保证模型达二阶精度，时间积分采用二阶龙格-库塔迭代法[22]。

第一阶段，采用投影法：

(3)

(4)

式中：Un为n时刻的U；U*为两步投影法的中间值；U(1)为最终阶段的估计值。

第二阶段，采用相同的投影法将速度场更新到第二阶段的中间值，然后采用Runge-Kutta算法计算得到n+1时刻的结果：

(5)

(6)

(7)

2.3 边界条件

为了求解相关方程，对所有物理边界设置边界条件。其自由面的边界条件[19]表示如下：

(8)

(9)

在自由面上动压力为0，对于k-ε模型，k和ε梯度为0：

(10)

在底部，规定了法向速度和切向应力，法向速度w通过运动学边界条件施加：

(11)

2.4 模型验证

利用偏差指数B和离散指数S进行模型验证：

(12)

(13)

式中：N为波高样本个数；Hm为数学模型结果；Ho为物理模型结果。偏差指数和离散指数越接近0，代表数学模型结果和物理模型结果越接近。图 2分别为在规则波和不规则波作用下通过可透浪斜坡式防波堤的波高数值模拟值(纵坐标)和物理模型试验值(横坐标)的对比。其中，规则波下B=0.011,S=0.121,不规则波下B=0.023,S=0.055。结果表明不论是规则波还是不规则波，NHWAVE模型都可以较好地模拟不越浪可渗透斜坡式防波堤的透浪过程。

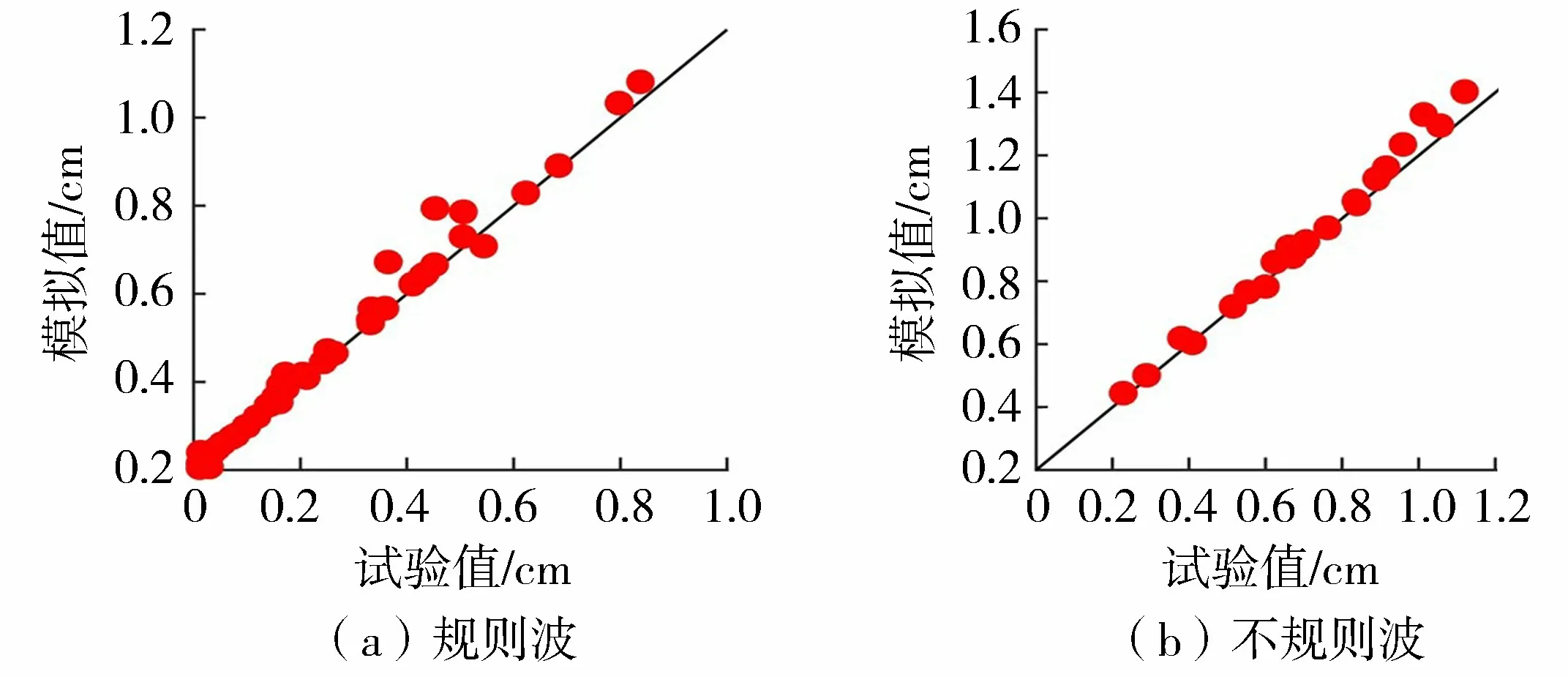
图2 堤后波高数值模拟值与物理模型试验值对比Fig.2 Comparison of numerically simulated wave height and measured wave height from physical experiments behind breakwater

2.5 模型数据

在数值模型验证良好的条件下，利用数值模型补充物理模型试验未能考虑的组次以得到适用范围更广的规律；同时建立多种条件下，通过斜坡式防波堤前后波高变化的试验数据库。其中，水深分别取为30 cm、40 cm；在静水面处物理模型试验堤宽分别为52.3 cm、78.5 cm、104.4 cm，在数学模型中换算成相对堤宽，分别为0.2、0.3、0.4；波高取为5 cm、6 cm、7 cm、8 cm、9 cm、10 cm、11 cm、12 cm、15 cm、20 cm；规则波下入射波周期为1.2 s、1.5 s、1.9 s、2.3 s，不规则波下谱峰周期为1.27 s、1.73 s、2.19 s、2.65 s。

3 试验结果与讨论

波浪与可渗透斜坡式防波堤相互作用时，大部分波浪能量被很快耗散，其中一部分波浪经堤身反射回去，一部分透过堤身传至堤后。透浪系数Kt是衡量防波堤透浪特性的关键指标，其物理含义为堤后透射波高与堤前入射波高的比值[23-24]。Kt的大小反映了透浪式防波堤消减波浪的能力，Kt越小，其消浪效果越强，透浪性越弱。在不越浪前提下，斜坡式防波堤的孔隙特性是透浪系数的重要影响因素，而孔隙特性与堤心石粒径有关。本文从堤心石粒径(D50)、入射波有效波高(Hs，i)、入射波周期(T)3个有因次量及相对堤宽(B/L，L为入射波长)、波陡(H/L)两个无因次量出发，分析上述因子对透浪系数的影响规律。

3.1 堤心石粒径D50的影响

从图3可以看出，在规则波或不规则波波况下，随着D50的增加，透浪系数逐渐增大，即D50越大，波浪越容易透过防波堤传入堤后水域影响堤后稳定。这是因为当粒径增大时，斜坡式防波堤孔隙率增加，导致透浪性增强。D50越小，防波堤消浪效果越好，其中，不规则波的变化大于规则波。对规则波来说，D50=0.5时，波浪衰减了99.4%，当D50增加到3.5，波浪衰减了98.7%，衰减幅度减小0.7%；而对于不规则波，D50由0.5增加到3.5，衰减幅度减小3%。很明显，不规则波变化幅度更大，且在同一粒径下，不规则波的透浪系数更大，这是由于在同一条件下，不规则波的随机性较强，波形杂乱。因此，在实际工程区域内，宜选用较小质量范围的块石作为防波堤的堤心石。

图3 堤心石粒径的变化对透浪系数的影响Fig.3 Influence of particle size of core material on transmission coefficient

3.2 入射波有效波高的影响

图4为堤前水深0.3 m，入射波分别为规则波和不规则波条件下，Kt随Hs，i的变化情况，其中蓝色、红色、黄色的点分别表示B/L为0.2、0.3、0.4。由图4可见，随着入射波波高的增大，各组次Kt均呈减小趋势，大部分呈线性递减且幅度较大，这与入射波波高增大会导致水体紊动消能效果更明显有关。此时，Kt的变化还与相对堤身宽度和入射波周期有关。图4显示，多数条件下，相对堤宽越小，Kt越大；周期越大Kt越大。图4(a)中，在规则波作用下，当T=1.5 s时，随着B/L从0.2增加至0.4，Kt由0.12下降至0.05；而当B/L=0.2时，随着T从1.5 s增加至2.3 s，Kt由0.12增至0.17。由于趋势线存在叠加、交叉的情况，Kt与波周期和波长的关系较波高更为复杂。

图4 入射波波高的变化对透射系数的影响Fig.4 Influence of incident wave height on transmission coefficient

3.3 入射波周期的影响

图5为Kt随T递增的态势，其中蓝色、红色、黄色的点分别表示B/L为0.2、0.3、0.4。堤前水深为0.3 m，在规则波情况下，T从1.1 s增大到1.9 s时，Kt随之明显增大，T继续增大到2.3 s时，波周期增大对Kt影响逐渐收敛；同样，在不规则波情况下，以有效波周期Ts代表入射波周期，当Ts从1.27 s增大到2.19 s时，Kt增大趋势明显，Ts从2.19 s增大到2.65 s时，Kt增长趋于平缓。综上，以长周期涌浪为例[25]，对规则波和不规则波，可透浪斜坡式防波堤后对较短周期波的消浪效果明显，但随着波周期的增加，其消浪效果逐渐削弱。从不同簇群可见，B/L影响透浪特性对入射波周期的响应。当B/L较大时，Kt随T递增的规律不再显著。

图5 入射波周期的变化对透浪系数的影响Fig.5 Influence of incident wave period on transmission coefficient

3.4 相对堤宽的影响

进一步选取B/L分别为0.2、0.3、0.4的试验数据作为分析对象，图6 对比了在规则波和不规则波条件下Kt随B/L的变化。由图6可以看出，Kt随B/L的增加而减小，这一规律对规则波和不规则波皆适用，且后者更显著(趋势线梯度为前者同条件下的1.5倍)。很明显当堤宽增加时，波浪与堤身作用时间加长，不同类型波浪损耗能量均变多。从破碎角度来看，当堤宽加大后，波浪更容易发生完全破碎，导致波能减少，最终使通过堤身的波高也减小，消浪效果较好。图6也显示了透浪特性与波陡(H/L)相关。随着H/L的减小，Kt增大，且随B/L递减的规律增强，这一特征在不规则波情况下表现明显。

图6 相对堤宽的变化对透射系数的影响Fig.6 Influence of relative dike width on transmission coefficient

3.5 波陡的影响

H/L是影响波浪破碎形态的重要因素，坦波较陡波更不易发生破碎，因此坦波波能损失较小，消浪效果不如陡波。图7为Kt随波陡倒数(波坦L/H)的变化规律。由图7可见，L/H越大，即波浪越平坦，Kt越大，即透浪性越强；且波陡对规则波的影响较不规则波显著，其透浪系数变化范围也更大。从能量角度看，入射波H/L越大，波浪在堤上越容易破碎，波浪与堤身相互作用更强烈，能量越容易损耗，穿过堤身的能量越少，Kt随之减小。

图7 L/H的变化对透射系数的影响Fig.7 Influence of wave steepness on transmission coefficient

4 经验公式拟合

由透浪系数影响规律分析可知，D、H、T、B/L、H/L对Kt都有影响。水深为0.3 m时，根据微幅波理论，相同水深下波周期变化对应于波长变化，采用H/L反映T对Kt的影响。此外，由于波陡已含波高因子，不再单独考虑波高对Kt的影响，堤心石粒径也转化为相对值。采用多元线性回归法拟合得到Kt的计算公式，并将得到的经验公式计算结果与物理模型试验结果进行对比分析并校核，在试验条件范围内(模型中T为1.1～2.3 s，H为5～20 cm，原型中T为6.0～12.6 s，H为1.5～6.0 m，Kt为0～0.2)规则波和不规则波情况下Kt计算公式分别为

(14)

(15)

为进一步验证式(14)(15)的准确性和适用性，在物理模型和数学模型试验数据的基础上，加入前人试验研究公开的数据(本文物理模型及刘涛等[26]、王登婷等[16]、丁坤等[5]的试验数据)，建立较完整的透浪试验数据库。利用数据库中的数据进行公式验证和比选。图8(a)为基于式(14)的规则波Kt计算值与试验值的对比，其相关系数为0.90。前期研究不乏关于不规则波透浪的试验数据，其中，Keulegan[27]讨论了石块堆筑的斜坡式防波堤与波浪的作用；Zanuttigh等[13]对波浪能量的透射展开了研究；葛晓丹等[15]研究了波浪与防波堤相互作用的波浪渗透问题。图8(b)为基于式(15)的不规则波Kt计算值与物理模型试验数据及相关文献试验值的对比，相关系数达0.95。结果表明，式(14)(15)可以应用于不越浪斜坡式防波堤的透射系数估算。

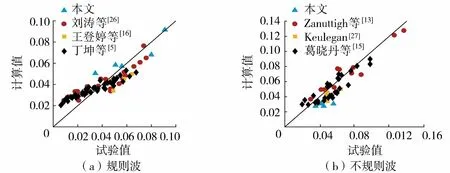
图8 规则波和不规则波作用下Kt 计算值与试验值的对比Fig.8 Comparison of calculated and experimental values of wave transmission coefficient Kt under regular wave action and irregular wave action

图9采用Ahren[28]、王登婷等[16]、习和忠等[14]、杨会利等[6]、葛晓丹等[15]给出的经验公式，分别在本文试验条件下进行Kt计算。从结果对比来看，习和忠等的计算结果偏差较大，比试验值大4～5倍，其原因是该公式基于斜坡式抛石堤，块石尺寸很大，堤身内部波高消耗较少，透过堤身波高较大。Ahren[28]和沼田淳给出的经验公式[15]计算值均大于试验值，这二者都是通过物理模型试验结果拟合得出的经验公式，Ahren[28]的物理模型试验由粒径单一的石块堆筑而成，块石重量满足常用护面块体重量范围，与习和忠有一定粒径范围的块体相比有所不同；沼田淳的物理模型试验[15]采用人工消波块体堆筑成的斜坡式防波堤，相比习和忠物理模型试验的堆石块体，消波块体使堤身内部波高消耗更大，导致渗透波高减小。王登婷等[16]给出的经验公式计算值也大于试验值，其断面试验中堤心石尺寸考虑了模型比尺的影响，并适当扩大了堤心石尺寸，使波能内部消耗减小。但对于工程应用，计算值大于试验值是偏于安全的，因此习和忠等[14]、Ahren[26]、沼田淳及王登婷等的公式[15-16]在实际工程应用时有一定的优势。杨会利等[6]和葛晓丹等[15]给出的经验公式计算值分布在试验值两侧，杨会利等[6]的离散度相对较大，主要因为其考虑实际工程，模型尺度更大且比尺更大，此时会存在黏滞力的影响。葛晓丹等[15]的公式采用王登婷等[16]的试验数据拟合得出，并在其基础上引入相对水深这一影响因素。对比图8与图9可见，本文推导的斜坡式防波堤Kt计算公式与试验结果较为吻合，有一定的优势。

图9 以往经验公式的Kt计算结果与试验值对比Fig.9 Comparison of calculated results from previous empirical formula and experimental results for wave transmission coefficient Kt

5 结 论

a.在其他条件不变时，透浪系数随堤心石粒径的增大而增大，且与入射波是否规则有关。

b.在波周期不变时，透浪系数随着波高的增大而减小，但在不越浪情况下波高对透浪系数影响较小。

c.在入射波波高不变时，透浪系数随入射波周期的增大而增大，且规则波变化较不规则波明显。

d.规则波和不规则波情况下，透浪系数均随着相对堤身宽度的增大而减小，在相同波浪条件下，不规则波时相对堤宽的影响比规则波更大。

e.相同入射波条件下，规则波和不规则波透浪系数均随波坦的增大而增大，不规则波情况下，波坦对堤后透浪系数更敏感。

f.综合上述波要素影响提出的透浪系数半经验半理论公式对试验数据拟合较好，相关系数均达0.9以上。因此，在本文数据库范围内，该公式可应用于不越浪-可透浪斜坡式防波堤透浪系数的估算。对范围外的情况，需结合物理模型试验进行确定。