往复流作用下潮流能水轮机单桩基础冲刷试验

陈汨梨，林祥峰，张明宗，张继生

(1.河海大学海岸灾害及防护教育部重点实验室，江苏 南京 210098； 2.中国港湾西部非洲区域公司，科特迪瓦 阿比让市 06BP6687； 3.河海大学港口海岸与近海工程学院，江苏 南京 210098)

随着世界各国对可再生清洁能源的日益重视，潮流能因其可预测性强、能量密度大等特点受到广泛关注[1-2]。在实际工程中，潮流能水轮机基础周围持续发生局部冲刷，最终可能引起机组整体失稳破坏[3]。此外，在海域中布置大规模潮流能水轮机阵列会影响周围海域的泥沙输运过程，改变周围海域的地形地貌[4]。潮流能水轮机单桩基础局部冲刷过程受单桩基础和水轮机叶轮的共同影响，导致前人基于单桩基础冲刷试验提出的冲刷预测方法低估了水轮机单桩基础局部冲刷深度[3]。水流经过水轮机叶轮时，由于能量提取，叶轮范围内流速减小，叶轮周围流速提高[5]。当水轮机靠近海床面时，叶轮周围流场发展受海床面限制，叶轮下叶尖和海床面之间的水流明显加速，流速提高最高可达7%[6]。叶轮下叶尖和海床面之间的加速流改变了海床边界层流速的分布，进而对海床的泥沙输运产生了影响。Ramírez-Mendoza等[7]发现，由于水轮机叶轮旋转的影响，在水轮机叶轮正下方会形成和流场特征相适应的马蹄形冲坑，而在远尾流场形成泥沙淤积。另一方面，水轮机叶轮与海床面间的加速流和下游单桩基础的相互作用改变了单桩基础周围的流场特性[8]，显著影响了单桩基础局部冲刷的发展过程[9-10]。基于物理模型试验，Chen等[11]发现单向恒定流作用下水轮机单桩基础最大冲刷深度随着叶轮安装高度的减小而增大，这是由于不同安装高度对水轮机叶轮正下方水流的加速效果不同导致的；Hill等[12]分别研究了定床和动床条件下水轮机单桩基础的冲刷过程，发现相比于定床条件，动床条件加大了水轮机单桩基础局部冲刷深度，最大冲刷深度发展具有周期性变化的特点；Lin等[13]研究了单向流作用时水轮机影响下单桩基础局部冲刷演变过程，发现冲刷过程受到来流条件、叶轮安装高度的显著影响，提出了水轮机单桩基础最大冲刷深度、冲刷坑形状的预测方法；Sun等[14-15]研究了叶轮直径、旋转速度和安装高度对水轮机基础冲刷发展的影响规律，结合量纲分析法提出了水轮机基础冲刷理论预测模型；Musa等[16]研究了水轮机阵列对复杂地形泥沙输运过程的影响规律。此外，数值模拟法也被广泛用于研究潮流能水轮机与海床面的相互作用。Zhang等[17]建立了水流-水轮机-海床面相互作用数值模型，分析水轮机对水流的响应过程及其影响下单桩基础局部冲刷演变过程；Yang等[18]结合促动线和大涡模拟方法，模拟了水轮机单桩基础局部冲刷发展过程，分析了不同床面形态对水轮机周围流场发展的影响。

综上可知，潮流能水轮机基础局部冲刷过程是近年来潮流能开发利用研究的热点之一，研究潮流能水轮机影响下基础冲刷演变特性对其单桩基础防护和结构稳定具有重大意义。潮流能水轮机基础局部冲刷过程受到水轮机叶片形状、水轮机下叶尖与床面间距、水轮机直径、水轮机运行状态等众多因素的影响[3]，现有研究多关注单向恒定流影响下水轮机单桩基础局部冲刷发展过程，而针对流向改变情况下水轮机单桩基础冲刷的研究尚未见报道。本文试验研究了往复流作用下潮流能水轮机单桩基础局部冲刷演变特性，可为实际潮流能水轮机基础冲刷防护设计提供参考。

1 试验方案

1.1 水槽与泥沙参数

试验在山东交通学院港航水动力实验室的大型波流水槽中开展。水槽长50 m，宽1.2 m，高1 m，两侧为光滑透明有机玻璃板，如图1所示。在水槽中间段设置沙槽试验段，沙槽长10 m，宽1.2 m，深0.2 m，沙槽两侧采用水泥浇筑1∶4斜坡，使得水流能够平缓进入沙槽试验段，减弱试验过程中由于水流不稳定而对沙槽中泥沙输移产生的影响。采用双向泵驱动水流，在水槽前后两端设置蜂窝稳流装置，可有效消除水槽前后进、出水口产生的大尺度涡旋，从而稳定、平缓水流。

图1 水槽试验布置(单位：m )Fig.1 Scheme of experimental set-up in the flume (unit: m)

试验采用均匀粗砂，泥沙中值粒径D50=0.80 mm，分层系数σ=1.22，密度ρ=2.65 kg/m3。试验水深保持恒定(H=0.54 m)，根据Melville[19]计算得到泥沙临界启动流速vc=0.42 m/s。在沙槽两端靠近斜坡处均匀喷砂胶水，防止水流通过斜坡进入沙槽试验段时引起冲刷。

1.2 水轮机设备

试验采用双向造流，考虑对称性，将水轮机布置在沙槽中心位置，距离沙槽前、后端均为5 m，距离水槽两侧均为0.6 m。如图2(a)所示，水轮机为三叶片水平轴潮流能水轮机，制作材料为不锈钢，叶片采用数控机床加工。水轮机由叶轮、轮毂和单桩基础构成，叶轮直径D=0.27 m，轮毂直径为0.15D，轮毂长度为0.87D，单桩基础中心与叶轮中心间距为0.35D，单桩基础直径为Dp=0.1D。试验开始前，即平坦床面下，水轮机下叶尖距离海床面高度为0.35D(图2(b))。试验过程中，水轮机在水流驱动下自由旋转，叶尖速比保持稳定，约为4。水轮机模型单桩基础埋深为整个海床面高度，为0.2 m。

图2 水轮机模型及其尺寸Fig.2 Turbine model and its size

1.3 试验工况

在单桩基础局部冲刷过程中，桩前下潜流、桩侧马蹄涡系和桩后尾迹涡流起主要作用[9]，而其强度和来流速度紧密相关。本次试验考虑4组流速情况下的单桩基础局部冲刷演变过程。此外，为了说明潮流能水轮机运转对基础局部冲刷过程的影响，设置仅单桩基础工况作为对比。因此，共设置5个工况，来流速度由0.30～0.38 m/s，相应水流强度：

FI=v/vc

式中v为来流速度。水流强度变化范围如表1所示。图3为不同来流速度下的流速垂向分布。

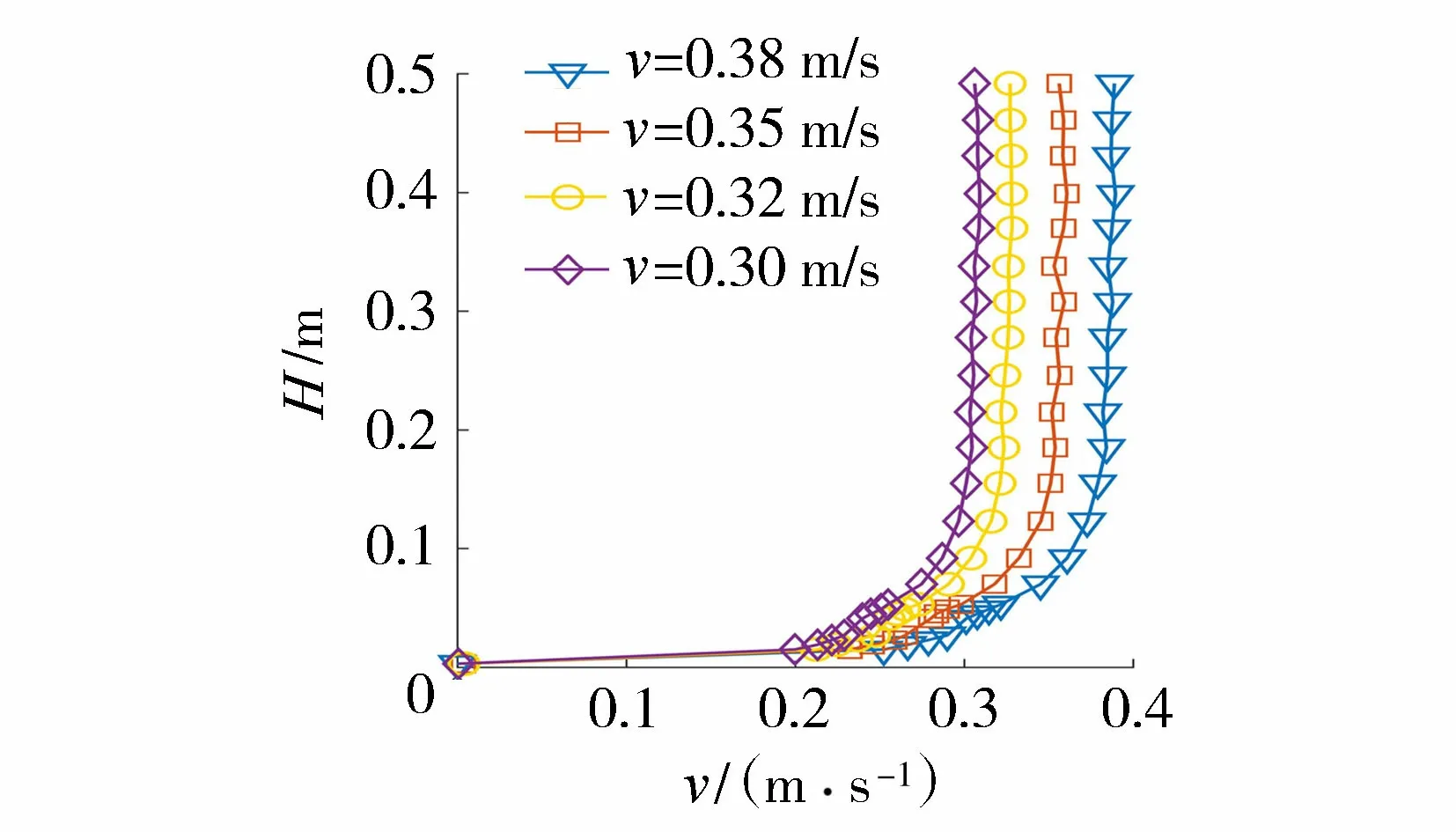
图3 不同来流速度下的流速垂向分布Fig.3 Vertical distribution of flow velocity with various inflow velocity

表1 试验工况设置

Schendel等[20]研究了单桩基础在半日潮作用下局部冲刷演变过程，冲刷时长为8 h，周期为2 h。参考Schendel等[20]的研究，采用往复恒定流，每组试验同样持续8 h，每冲刷1 h改变流速方向(周期2 h)，共4个周期(图4(a))，用以研究往复恒定流条件下潮流能水轮机单桩基础前期局部冲刷特性。为了测量试验过程中单桩基础冲刷深度发展过程，在单桩基础表面粘贴格尺纸(图2(a))，在格尺纸表面均匀标注4个位置，分别位于单桩基础前后和两侧。在试验过程中，每间隔10 min人工读取一次格尺纸上读数，进而获得相应时刻冲刷深度，如图4(b)所示。

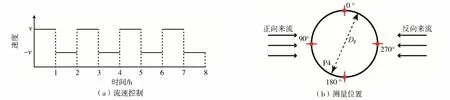
图4 试验流速控制及单桩周围测量位置Fig.4 Velocity control and measured locations around the mono pile

1.4 试验步骤

在试验开始前铺平沙槽，然后缓慢上水，防止上水过程中对初始沙床面的干扰。待水深达0.54 m、水槽内水体稳定后，控制双向泵运行功率，使水流达到预定流速。在试验过程中，采用多普勒流速测量仪监控水轮机叶轮上游2D处流速，保证水流的稳定性。之后每间隔1 h改变泵的运转方向，旋转水轮机叶轮和轮毂，使得水轮机叶轮始终朝向来流方向。每组工况持续8 h，每个小时内间隔10 min读取绕桩周4个测量位置的冲刷深度。

2 试验结果与讨论

2.1 冲刷过程

选取一组代表性的水槽试验结果对往复流作用下潮流能水轮机单桩基础局部冲刷过程进行分析。在v=0.38 m/s、FI=0.90工况下，桩周4个测量位置随时间和冲刷深度的变化过程如图5所示，其中S为测量位置处冲刷深度。由图5可知，桩周上下游冲刷深度呈显著周期性变化，而桩周两侧冲刷深度逐步提高，并无显著的周期性变化特点。分析其原因，主要是水流流向改变时，冲刷坑内马蹄涡方向改变，当测量位置由上游变为下游，坑内的泥沙被迅速带往该处，在该测量位置形成堆积，导致冲刷深度迅速减小；当测量位置由下游变成上游时，测量位置处的冲刷动力由桩后强度较低的尾迹涡流转化为强度较高的下潜水流，冲刷速率显著提高。随着冲刷的发展，冲坑、冲刷深度均逐步加大，桩上游下潜流的掏刷效果逐渐减弱，测量位置处冲刷深度周期性变化的幅度也相应减弱。在冲深坑内，泥沙由桩基上游被冲刷坑内的马蹄涡带往下游，几乎不在桩基两侧落淤。因此，桩基两侧冲刷深度呈逐步增加、无明显周期性的特点。此外，尽管桩基上、下游两侧冲刷深度周期性变化，但是整体冲刷深度逐渐提高，表明随着时间不断推进，冲刷坑内的泥沙被逐渐带出冲刷坑外，冲刷坑内被往复流前后搬运的泥沙量逐步减少。

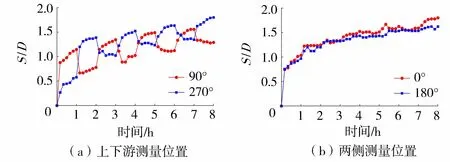
图5 典型工况下各测量位置冲刷过程Fig.5 Scour progress at measured locations in typical test condition

图6为每进行1 h桩周各测量位置处相对冲刷深度(S/Dp)随时间的发展变化。由图6可以看出，最大冲刷深度始终位于单桩基础上游，最小冲刷深度位于单桩基础下游，上下游的位置会随着来流方向的转变而相互变化；桩基两侧的冲刷深度逐渐增加。随着冲刷的发展，前后2 h内桩周各测量位置冲刷深度变化逐渐减小，各位置处的冲刷深度逐渐接近，表明随着冲刷坑的变大，冲刷坑内可被水流前后搬运的泥沙逐渐减少，冲刷坑形态趋于平衡、稳定。在每个周期的第2 h内，当桩柱上游转变为下游时泥沙快速淤积，之后此处冲刷深度也逐渐发展，但是冲刷深度始终未超过前1 h，表明尾迹涡流未能将在此处淤积的泥沙完全带出冲刷坑外。而当单桩柱由下游转变为上游时，冲刷深度快速发展。但由图6可看出，这些差异随着冲刷发展逐渐减小，冲刷过程逐渐变缓。

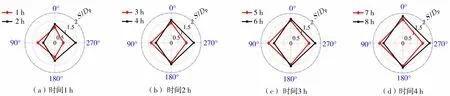
图6 桩周各测量位置变化情况Fig.6 Scour development for measured locations around the pile foundation

2.2 与仅单桩工况对比

在潮流能水轮机运行影响下，水轮机下叶尖和海床面之间的水流被加速，进而改变了下游单桩基础的来流条件[6]，图7为v=0.38 m/s、FI=0.90工况下水轮机模型和仅单桩基础工况下最大冲刷深度的对比，其中Smax为桩周最大冲刷深度。在冲刷过程中，水轮机模型和仅单桩工况的最大冲刷深度均随着来流流向的改变发生周期性震荡，最大冲刷深度均逐步增加。水轮机模型引起的最大冲刷高于仅单桩工况，而且随着冲刷的发展，两者的差距逐渐增加。在第一个冲刷周期后(2 h)，水轮机模型比仅单桩工况的最大冲刷深度多0.15Dp；而在试验结束后(8 h)，水轮机模型比仅单桩工况的最大冲刷深度多0.35Dp，表明在冲刷过程中水轮机的影响在逐渐累积，使得两种工况的冲刷深度差距逐渐增加。同时也表明，针对单桩基础或桥墩的冲刷深度提出的预测公式[9-10，19]低估了潮流能水轮机基础冲刷深度，这与前人的研究结论[3]一致。

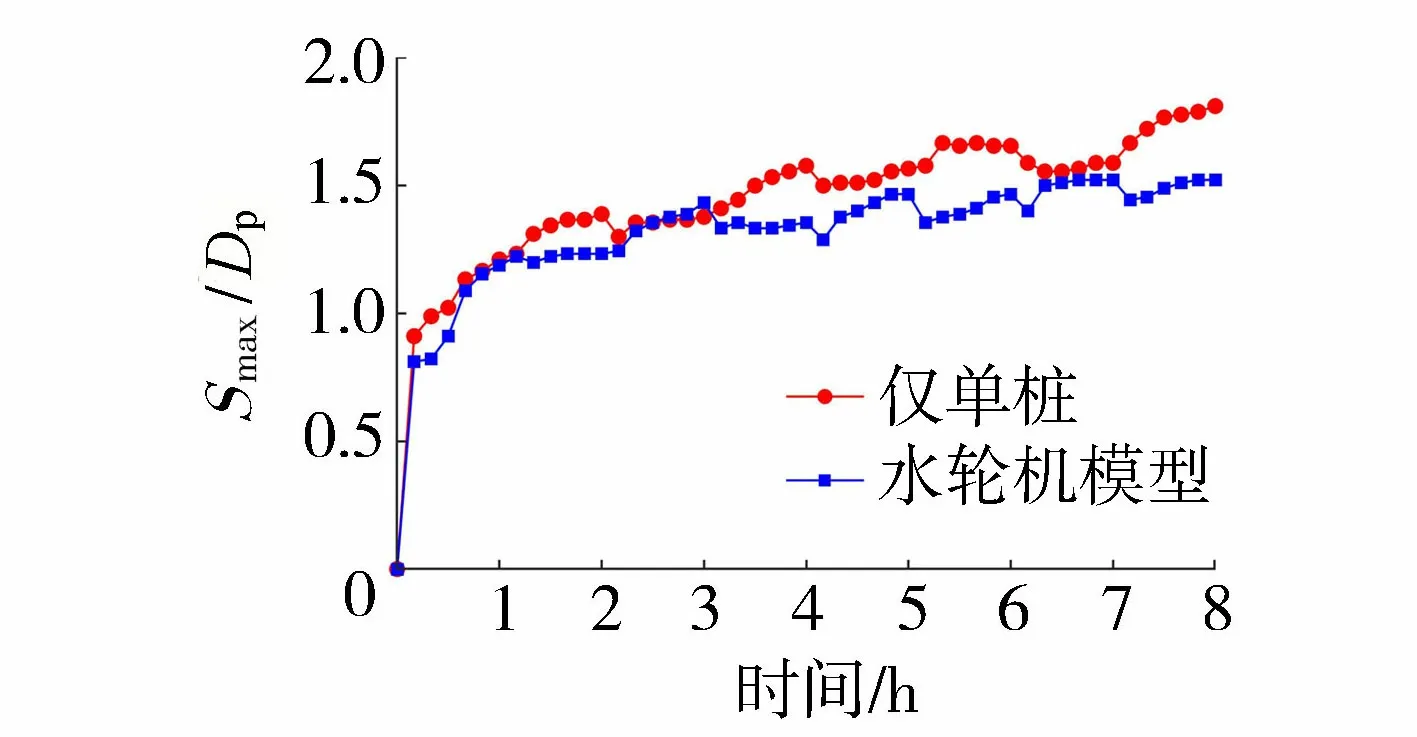
图7 仅单桩工况和水轮机模型最大冲刷深度发展对比 Fig.7 Comparison of maximum scour depth development in the case of single pile and turbine test

2.3 水流强度影响

水流强度对于单桩基础的冲刷特性具有重要的影响[9]，因此考虑了水流强度对于水轮机模型单桩基础冲刷过程的影响。图8为不同水流强度下水轮机模型单桩基础局部最大冲刷深度的发展过程。在冲刷过程不同的水流强度下，水轮机模型中单桩基础周围最大冲刷深度均随来流流向的改变发生周期性震荡且逐步增加；而周期性震荡幅度随着水流强度的提高逐渐增加，表明随着水流强度的提高，冲刷坑内在单桩基础上下游来回输运的泥沙量逐渐增多。

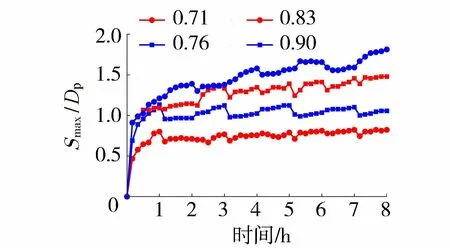
图8 不同水流强度下桩周最大冲刷深度发展Fig.8 Development of maximum scour depth under various flow intensity

图9为水流强度和试验结束时单桩基础最大冲刷深度的对应关系，其中Send为试验结束时单桩基础最大冲刷深度。由图9可见，试验结束时桩周最大冲刷深度随着水流强度的增加呈线性提高。当水流强度从0.71增加到0.90时，最大冲刷深度由0.8Dp增加到1.8Dp，提高了近125%。水流强度和冲刷深度的线性关系与前人关于仅单桩基础冲刷的研究结论相似[9]，表明水轮机的运行并未改变单桩基础局部冲刷的发展模式，而是加剧了单桩基础的冲刷发展进程。

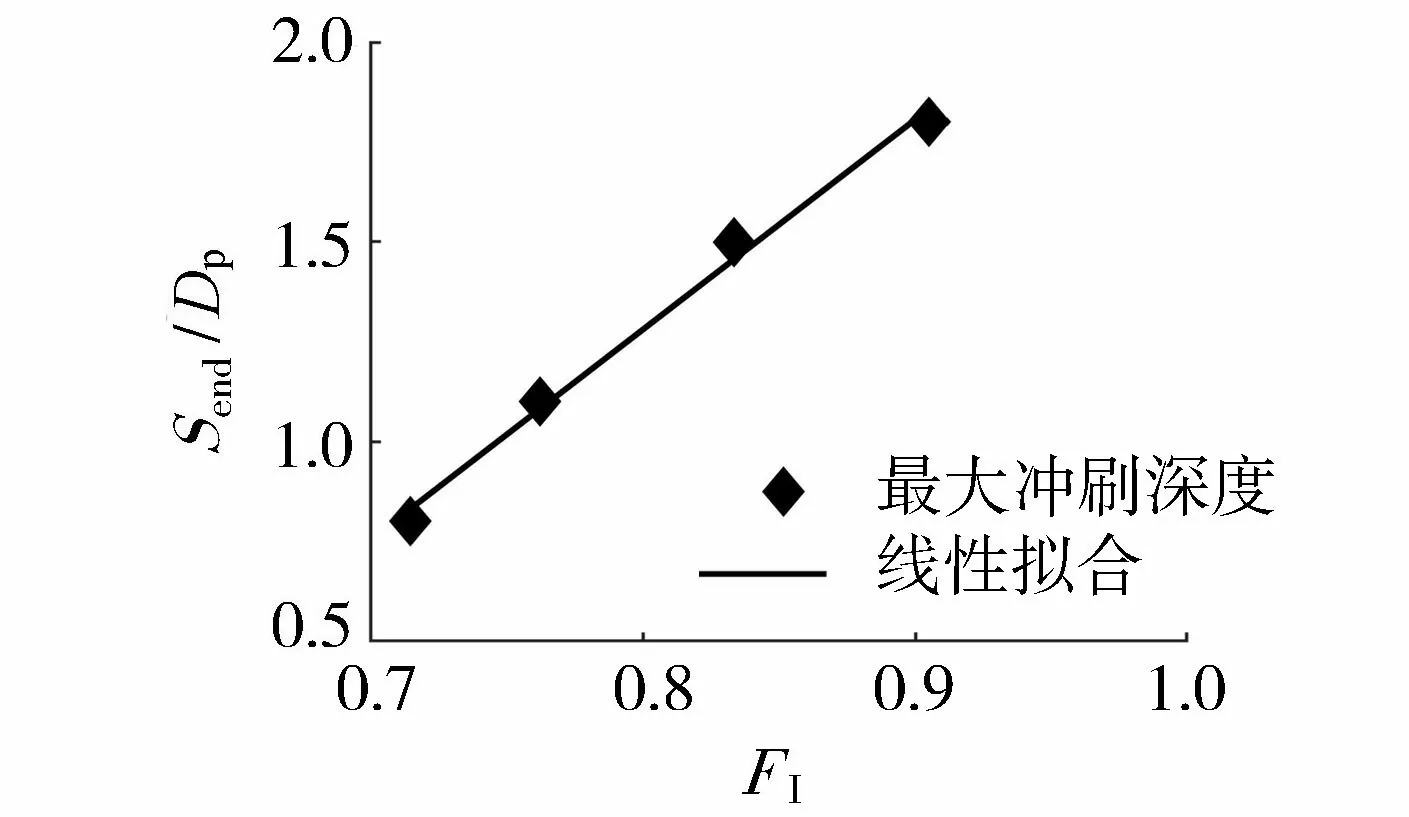
图9 试验结束时最大冲刷深度与水流强度关系Fig.9 Relationship between final maximum scour depth and flow intensity

2.4 与单向流作用比较

Lin等[13]研究了单向流作用下潮流能水轮机单桩基础局部冲刷演变过程，试验时长达24 h。为了与本文的双向流进行对比，取Lin等[13]前8 h的冲刷深度试验结果。表2为不同水流强度下单向流作用和双向流作用时潮流能水轮机单桩基础最大冲刷深度对比。由表2可知，双向流作用下单桩基础的冲刷深度均比单向流作用时小，这是由于双向流作用时，单桩基础周围的泥沙在基础附近往复运动，导致冲刷速率降低。此外，随着水流强度的增大，双向流作用与单向流作用下潮流能水轮机单桩基础最大冲刷深度逐渐接近。这是因为双向流作用下，当流速较小时，部分泥沙由于流向反转始终在冲刷坑内单桩基础上下游来回移动，无法被带出冲刷坑外；而随着流速增大，更多的泥沙在流向反转前被带出冲刷坑，使得冲刷深度显著增大。

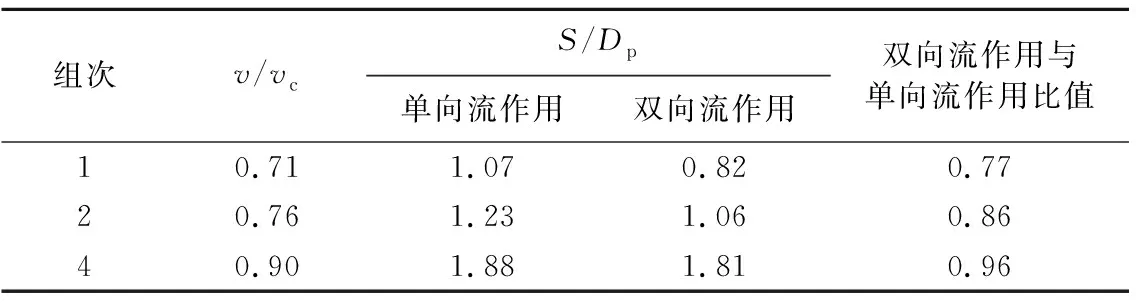
表2 单向流和双向流作用下冲刷深度对比

图10为分别在单向流和双向流作用下潮流能水轮机单桩基础冲刷深度与水流强度的关系。在单向流和双向流作用下，潮流能水轮机单桩基础冲刷深度与水流强度均呈显著的线性关系。由于流速较小时，单向流作用和双向流作用差异较大，随着流速的增大，两者差异逐渐减少，导致双向流作用时的线性斜率显著高于单向流作用。

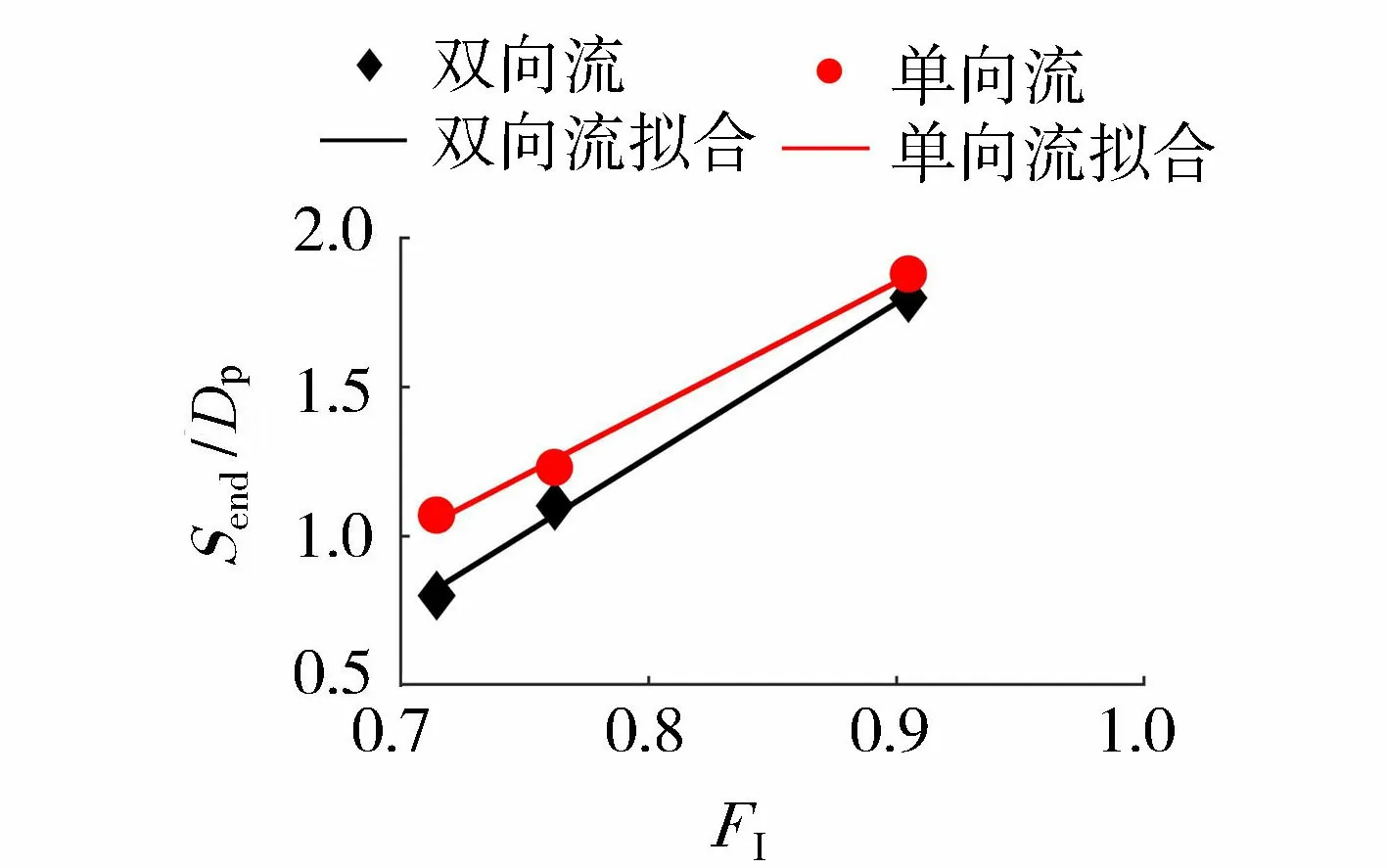
图10 单向流和双向流作用下冲刷深度与水流强度关系对比Fig.10 Relationship comparison of scour depth and flow intensity between directional flow and bidirectional flow

3 结 论

a.往复流作用下，潮流能水轮机单桩基础局部冲刷过程会随着水流流向改变发生显著的周期性震荡，最大冲刷深度在震荡过程中逐步提高。

b.相比于仅单桩工况，水轮机影响下单桩基础的冲刷过程明显加快，且它们的差异会随着冲刷进行更加明显。

c.平衡冲刷深度随着水流强度的提高呈线性增大，最大冲刷深度震荡幅度也随着水流强度的增加而提高。

d.相比于单向流作用，双向流作用下潮流能水轮机单桩基础冲刷深度较小，但随着水流强度的提高，两者差异逐渐减小。