站点乘客总候车时间计算方法优化研究
张海燕,郑长江,马君泽
(河海大学土木与交通学院,江苏 南京 210098)
引 言
公交车辆作为公共交通的重要组成部分,对提高城市道路资源利用率、缓解交通拥堵、降低交通污染具有重要作用。合理的公交车辆运营与调度安排能够增加公交出行对居民的吸引力,而获取准确的乘客候车时间是进行公交车辆时刻表编排及运营调度的数据基础。
乘客的候车时间受乘客到达特性和车辆到达特性两个因素的影响,当公交车发车频率较高时,乘客到达可认为是均匀分布,乘客的人均候车时间约为车头时距的 1/2[1-3];张腾飞[4]、张蕴琦[5]计算乘客在各站点候车时间时假设乘客到达服从均匀分布,以研究时段内发车间隔的1/2作为人均候车时间;李悦超等[6]、许梦菲[7]假设研究时段内乘客到达的数量服从泊松分布,利用当乘客到达服从泊松分布时,其相继到达的间隔时间服从负指数分布这一理论计算乘客候车时间;张晓春等[8]采用非时齐泊松过程理论构建了乘客到站模型,给出一种离散条件下的乘客人均候车时间计算方法。Gong等[9]、吴丽娟等[10]分别利用对数分布、正态分布和伽马分布等来拟合乘客到站时间分布规律,对乘客候车时间模型进行优化,并得出结论:发车间隔可靠性也会影响客流的分布。
总的来说,目前国内外对于乘客候车时间的计算方法多基于统计学理论,首先研究乘客的到站时间分布规律,再将拟合分布的概率密度积分求得人均候车时间期望,最后乘以研究时段内到达乘客总数计算站点乘客总候车时间。然而,在实际情况中,由于公交站点地理位置不同,乘客出行受电子站牌、手机到站提示等科技应用的影响,乘客的到站规律多变,单一的概率分布模型并不能贴切地在较长时段内描述乘客的到站规律。针对上述问题,本文提出一种基于公交IC卡或客流计数器数据拟合乘客累计到站数量曲线的乘客候车时间计算模型,采用代数学的方法,计算出时段内各乘客的估计到站时刻,并进一步求得站点乘客的总候车时间。
1 模型建立
1.1 模型假设
由于站点乘客候车情况多样,且到站公交车类型不同,为方便模型建立,提出以下假设条件:
(1)IC卡的刷卡数据近似等于所有上车乘客数,客流计数器均工作正常;
(2)公交车的容量足够大,不存在乘客滞站的情况;
(3)每位乘客仅等待一辆公交车,等待过程中不离站;
(4)车辆到站后乘客立即上车,车辆停靠时间忽略不计;
(5)仅研究单线公交上车乘客的候车时间。
1.2 数据预处理
大部分城市内公交车均装载有刷卡机和客流计数器等设备,能够记录乘客的上车时间、上车站点等数据。其中刷卡机记录的数据信息类型包括时间信息、乘客信息、位置信息、费用信息、车辆信息;客流计数器系统的数据内容包括车辆到站信息、乘客上下车数量等。
两者采集的数据内容示例如表1-2所示。

表1 公交车刷卡机采集信息示例

表2 公交车客流计数器采集信息示例
可见,在站点上车乘客总数这一数据上,客流计数器统计更加直观,为满足建立模型所需数据类型,需整理出某一时段内站点的各班次车辆上车乘客数量。为此,对于刷卡机数据,将统计时段内需求站点的刷卡信息按照车辆ID进行计次累加;对于公交客流计数器数据,按照到站时间先后顺序筛选出统计时段内所需数据。经过对原始数据初步处理,得到如表3所示的各班车辆到站时刻及上车人数数据表。
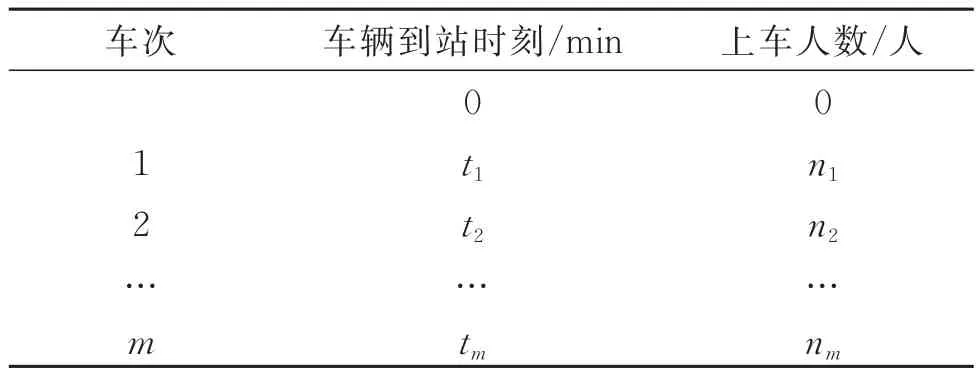
表3 各班车辆到站(站点A)时刻及上车人数表
在得到各班车辆到站时刻及上车人数数据后,为拟合站点累计到站乘客数量与时间关系函数,需统计时段内各班车辆到站时刻的累计上车乘客数量,将其作为站点累计到站乘客数量。将表3中各时刻上车人数累加,得到各时刻t对应累计到站乘客数量S的数据表格,如表4所示。
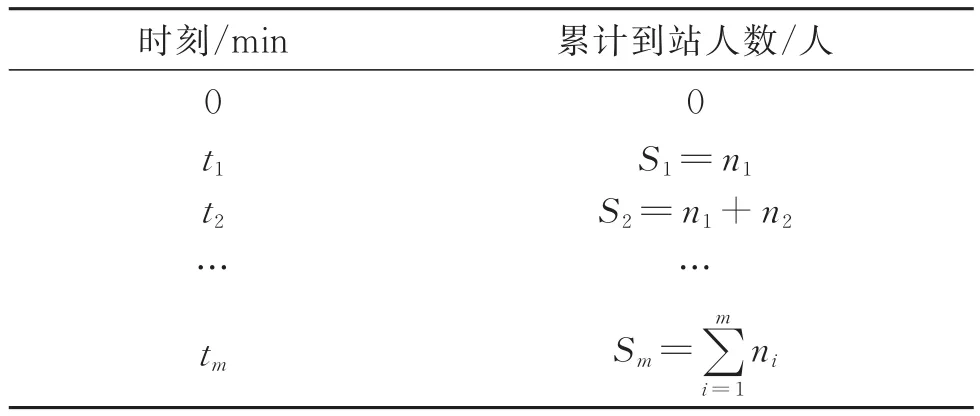
表4 各时刻累计到站(站点A)乘客数量表
1.3 模型建立
为求解时段内各乘客估计到站时刻,需拟合累计到达人数Sm关于时刻tm的关系函数。岳大振[11]采用三次样条插值方法拟合全天运营时段内线路的公交客流期望到达率曲线,由于本文拟合的数据类型为累计到站乘客数量,具有单调不减的性质,参考上述文献,采用较为相似的分段三次埃尔米特插值法进行拟合,图1为同一组离散数据点采用分段三次埃尔米特插值法与三次样条插值法的拟合结果对比图。
由图1中示例可以看出,相比于三次样条插值法,分段三次埃尔米特插值法拟合曲线更加平缓稳定,震荡现象不明显,且拟合曲线具有单调不减的特性,对于数据量无严格要求,因此本文采用分段三次埃尔米特插值法进行累计到站乘客数量与时间关系的拟合。记站点累计到站乘客数量与时间的函数关系为f,拟合后得到累计到站乘客数量S关于时间t的插值多项式f(t):
求解S=1,2,3,…时对应t的值,即可得到Sm位乘客的估计到站时刻p1,p2,…,pSm,求解过程伪代码如下:
在得到各个乘客的估计到站时刻后,可进一步求解时段内乘客总候车时间,以第一辆公交车与第二辆公交车到站时间间隔[t1,t2]为例,该时间间隔内n2位乘客的候车时间之和为:
则对于时段[0,tm]内所有到站乘客,总的候车时间T的计算公式如下:
式中T表示时段内站点乘客总候车时间;m表示时段内到站的公交车总数;ti表示时段内第i班车到站时刻,Sm表示该时段内累计到站乘客总数。
2 案例分析
以佛山公交309路12月1日晚高峰时段(18:00-19:00)清晖园站台为例,计算该时段内站点乘客累计候车时间,对模型的正确性和有效性进行检验,309线路为佛山市顺德区鸿运公共交通有限公司管辖下的一条市区线路,起始终点为顺德客运总站——羊额官沙村,全程17.3 km,运营时间为6:30~22:00。清晖园站点位于清晖园景点东北角,临近新世界中心商场,非工作日站点日均上车乘客总人数约为500人。首先对309路客流计数器数据进行处理,得到晚高峰时段(18:00~19:00)清晖园站点累计到站乘客数统计如表5所示。

表5 清晖园站点累计到站人数
使用分段三次埃尔米特插值法对累计到达乘客数量进行拟合,拟合图像如图2所示。可见,在晚高峰时段,累计到站乘客增长速率一直维持在较高水平,在40~50 min时增长速率略有放缓。
运用MATLAB软件求解累计到站乘客数为整数时各自对应时刻,即为各乘客的估计到站时刻,计算结果如表6所示。
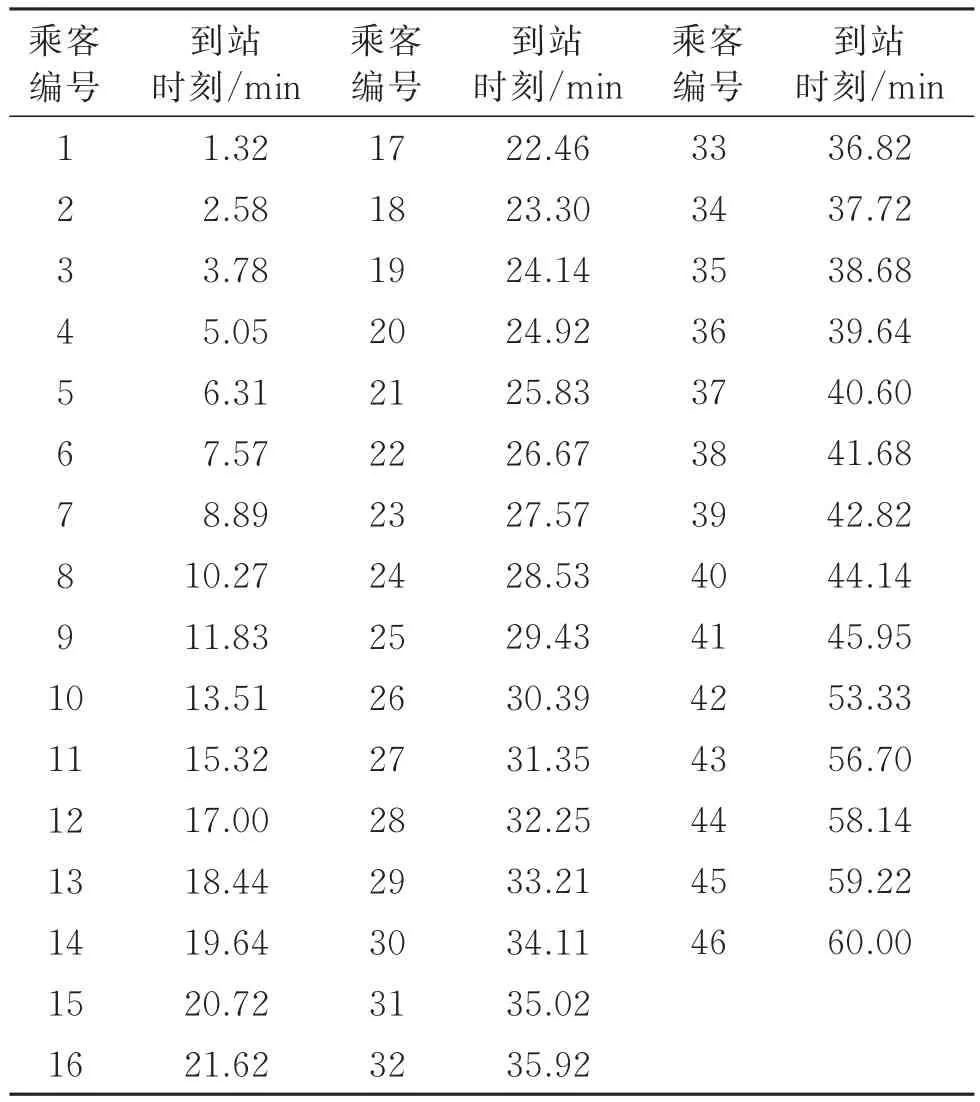
表6 乘客估计到站时刻
由于本案例中并未出现到站公交车上车乘客数为0的情况,因此,累计到站乘客数量与时间两个变量在数值关系上一一对应,可以采取拟合时间关于累计到站乘客数量关系的函数曲线的方法,来化简求解各乘客估计到站时刻这一步骤。
首先采用分段三次埃尔米特插值法拟合时间关于累计到站乘客的函数曲线,曲线拟合结果如图3所示。
将累计到站乘客数S=1,2,3,…,46带入函数g(S)=t求得各个乘客的预估到站时间,经检验,所得结果与表6一致。
将各乘客估计到站时刻P带入式(4),进一步求得晚高峰时段内清晖园站点乘客总候车时间为131.12 min。
3 结果对比与分析
3.1 结果对比
为验证方法有效性,将计算结果与采用假设乘客到达服从均匀分布与泊松分布的方法进行对比,下面将基于两种分布的方法分别命名为方法一、方法二进行计算,参考文献[4-7]中候车时间计算模型,将文章中各参数符号用本文中符号替代化简后,得到假设乘客到达服从均匀分布的候车时间计算公式(方法一)如下:
假设乘客到达服从泊松分布时,乘客总候车时间计算公式(方法二)如下:
将案例中参数代入式(5)和(6)中,分别计算两种方法所得乘客总候车时间,与本文结果进行对比,计算结果如表7所示。
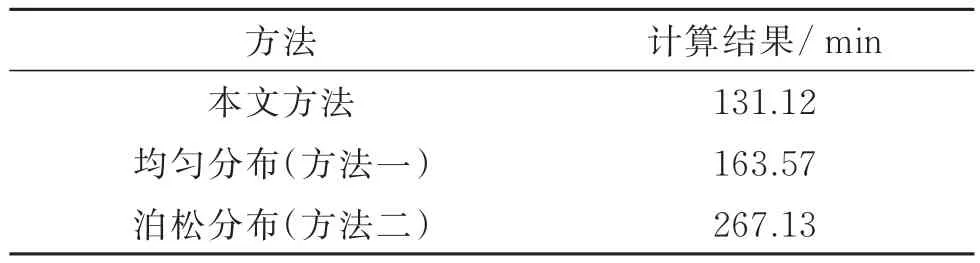
表7 各方法计算结果
可见,方法一与本文结果相近,相差19.8%,而方法二则与另外两种计算方法结果相差较大,约为两倍。
3.2 分布检验
为进一步比较案例中客流到站规律与泊松分布的差异,取高峰时段乘客平均到达率作为拟合泊松分布的期望值,即取λ=0.77,使用χ2拟合检验法验证清晖园站点晚高峰时段单位时间内到站乘客数量是否服从均值λ=0.77的泊松分布,其中显著性水平取α=0.05。计算结果如下:
故在显著性水平0.05下拒绝假设“单位时间内到站乘客数量服从泊松分布”。在非工作日晚高峰时段,由于清晖园站点地理位置临近旅游景点及商场,结束旅游或购物活动的乘客往往结伴前往站点候车,造成乘客到站特性与泊松过程[12]中要求的独立性不相吻合,即各乘客到达情况不相互独立,从而导致乘客的到站规律与不符合泊松分布。此类情况下采用方法二进行计算,将造成计算结果产生误差。
3.3 误差分析
进一步分析,方法二与其他两种计算方法结果相差较大,不单由乘客到达不服从泊松分布这一因素造成。多数以乘客到站服从泊松分布为假设前提的乘客候车时间计算模型以乘客相继到达的间隔时间服从负指数分布这一理论为基础进行建模,以文献[7]为例进行分析,首先由“当乘客到达服从泊松分布时,乘客相继到达的间隔时间t服从负指数分布”这一理论基础得出客在相邻两车时间间隔[0,h]内随机到达的概率密度函数为:
式中f(t)为乘客到站时间间隔的概率密度函数,λ为时间间隔内乘客到达率,单位为人/min。
随后求出单个乘客在相邻两车时间间隔内的候车时间期望T单:
则相邻两车时间间隔所有乘客的总候车时间即为到站人数λh乘以单个乘客的候车时间期望:
从T总的表达式中可以看出,该计算结果与假设乘客到达服从均匀分布时总候车时间相比,近似于结果的两倍,接近于表7中案例计算结果。
3.4 方法二优化
进一步分析,方法二的候车时间计算模型中,时间间隔内单个乘客的候车时间期望实际上为首个乘客的候车时间期望,对于之后到站的乘客,其候车时间期望计算时积分下限应与首个乘客不同。对此,可采取以乘客到站时间间隔为基础的方法进行改进。对于符合泊松流到站的乘客,由于其相继到达的间隔时间t服从负指数分布,则在相邻两车时间间隔[0,h]内,各乘客间到站时间间隔期望P为:
则时间间隔[0,h]内λh名乘客的总候车时间T总为:
式中iP表示第i位乘客的期望到站时刻。
对总候车时间T总进行进一步化简,步骤如下:
可见,经改进后,假设乘客到达服从泊松流的总候车时间计算结果与方法一的总候车时间相比,结果较为近似。将文中案例数据带入改进后的模型中,计算可得乘客总候车时间为146.30 min,与另两种方法结果均较为接近。
3.5 有效性验证
为验证本文方法与优化后方法二的有效性,采用假设性案例进行检验:假设某站点A在20 min内到站乘客20名、公交车4辆,采用随机函数生成20名乘客的到站时刻与公交车到站时刻。为方便计算,公交车到站时刻均设置为整数分钟,随机生成结果如表8所示。
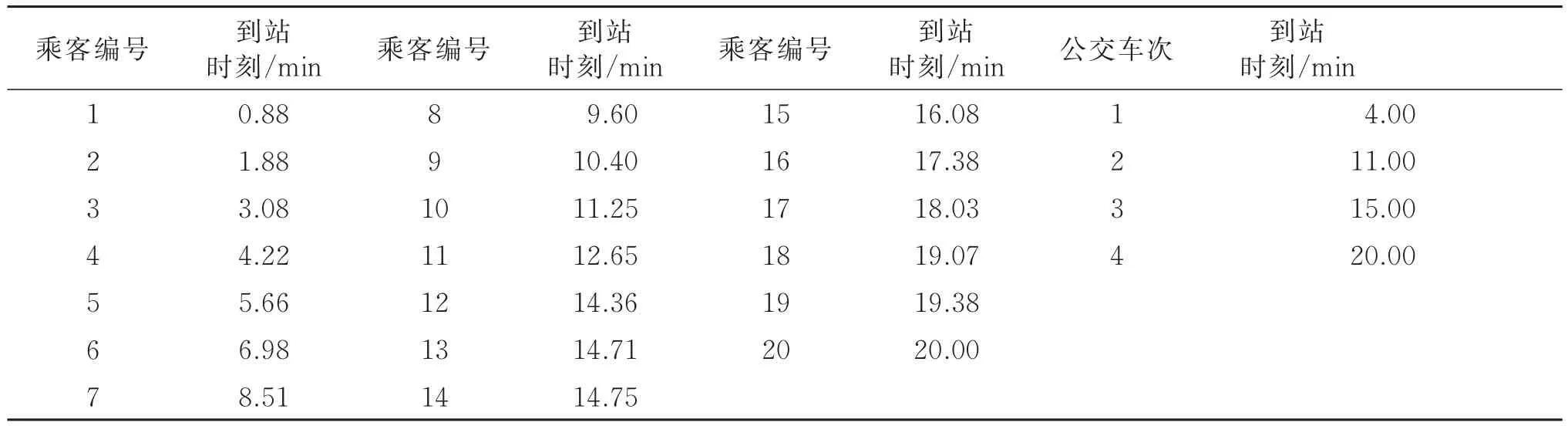
表8 乘客及公交车辆到站时刻随机生成结果
将上述假设性案例数据代入各方法进行计算后,得到各方法结果与误差比例如表9所示。
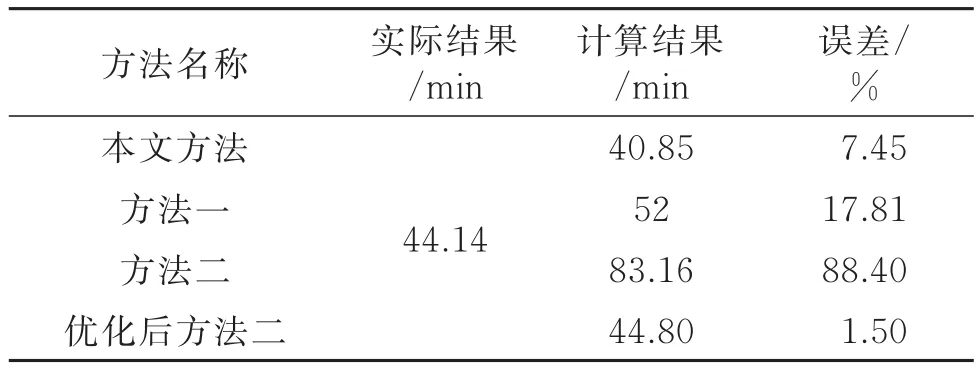
表9 各方法计算结果及误差比例
由表9中结果可以看出,本文方法与优化后的方法二在计算站点乘客总候车时间上的误差比例明显小于另两种方法,且准确度较高,验证了本文方法及改进后方法二的有效性。
4 结 论
本文研究了基于累计乘客到站拟合函数的乘客候车时间计算方法,采用公交车IC卡或客流计数器数据,计算各时段站点乘客候车时长。研究的主要结论包括以下几个方面:
1)建立了基于累计乘客到站数量拟合函数的乘客候车时间计算方法,通过求解拟合函数因变量在区间内整数变化时对应自变量的值,计算出各个乘客的估计到站时刻,进而得出站点乘客总候车时间,模型适用性广泛,能够直观反映站点客流到站规律;
2)利用佛山公交309路清晖园站点公交车客流计数器采集数据进行实例分析,计算出该站点晚高峰时段站点乘客总候车时间,便于公交公司对该线路运营计划进行调整和优化。
3)将本文方法与假设乘客到达服从均匀分布和泊松分布的站点乘客总候车时间计算结果对比,泊松分布结果差异较大,经检验晚高峰时段清晖园站客流到站规律不符合泊松分布。
4)对假设乘客到站服从泊松分布的候车时间计算模型进行了改进,并使用假设性案例对本文模型以及改进后的方法二进行有效性验证,结果显示两者计算准确度均较高。
综上,本文设计了基于乘客累计到站数量拟合函数的乘客候车时间计算方法,避免由于乘客到站分布规律变化而对候车时间计算准确度产生的影响,使得模型的适用条件更为广泛,为公交公司提供了新的乘客等车时间计算方法,方便公交公司优化公交时刻表,进而提升运营效率。

