非合作无源探测中的参考信号提纯新方法

应涛,王雪宝,田威,周成,侯小阳

1.海军工程大学 电子工程学院,武汉 430033

2.海军士官学校 电子对抗雷达声纳系,蚌埠 233012

非合作无源探测系统是利用第三方非合作辐射源发射的信号探测目标的双/多基地无源雷达系统。该系统本身不发射能量,而是被动地接收目标散射的非合作辐射源电磁信号,对目标进行探测、定位及跟踪,具有战场生存能力强、成本低、反隐身能力强等诸多优点,因此受到各国军方重视。目前,非合作无源探测系统利用的第三方辐射源信号除FM 广播信号、数字广播信号、卫星信 号、WIFI信号、UMTS 信号以及GSM 信号和LTE 信号等民用辐射源信号以外,还包括己方或敌方非合作雷达等军用辐射源信号,英国雷卡公司防御系统分部利用伦敦盖特威克机场的远程空管雷达开展了非合作无源探测系统的研究,国防科技大学选择预警机雷达信号作为辐射源信号,开展了基于空基辐射源的非合作无源探测系统关键技术研究。战时,由于可利用的民用辐射源匮乏,利用己方或敌方雷达作为辐射源进行非合作无源探测将变得尤为重要。线性调频(Linear Frequency Modulation,LFM)信号作为一种时宽-带宽积较大的信号,具有低截获概率特性和较好的抗干扰能力,广泛应用于雷达系统。因此,本文将以发射LFM 信号的雷达作为非合作辐射源,开展非合作无源探测系统中参考信号的提纯研究。

非合作无源探测系统有2个接收通道,即接收辐射源直达波作为参考信号的参考通道和接收目标散射回波的监测通道。参考通道中的直达波参考信号主要有2个方面的作用：①监测通道接收到的目标回波中,往往伴随着大量的直达波干扰和多径杂波干扰,且功率远大于目标回波,这对目标检测造成很大干扰。这时,需要纯净的参考通道直达波信号作为参考信号,抑制监测通道的直达波干扰和多径杂波干扰；②参考通道直达波信号作为二维互相关检测的参考信号,参考信号的纯净程度将直接决定系统的检测性能。但在实际情况中,参考通道接收到的辐射源直达波信号不可避免地受到多径信号的干扰,是辐射源直达波信号及多径杂波信号的叠加,参考通道为监测通道提供的参考信号不再“纯净”,对系统探测性能造成严重影响。

目前,获取“纯净”直达波参考信号主要有2条技术思路,即“重构”和“提纯”。“重构”是指基于辐射源信号的特殊结构特性,通过信道估计和同步解调来精确重构参考信号,文献[20]在压缩感知的匹配追踪算法基础上,利用数字地面多媒体广播信号的特性,提出了一种参考信号重构新方法。“提纯”则是利用时域和空域自适应滤波等方法,通过抑制参考通道接收信号中的多径干扰,获取“纯净”的参考信号,但提取信号纯度受限于天线方向性,且对参考通道接收天线提出了更高的要求。

当有用信号与干扰信号在时域或者频域上重叠时,要想将有用信号从干扰信号中提取出来,通常从有用信号的特性出发,考虑将混合信号变换到有用信号与干扰信号可分离的变换域上,然后采用滤波方法将有用信号提取出来。通常,在进行非合作无源探测系统设计和部署时,会对辐射源信号进行调研和分析,获取有关先验知识,因此可对辐射源信号特性进行研究,并充分利用辐射源信号的这些特性,将参考通道中直达波与多径的混合信号变换到对信号时延敏感的变换域上,在此变换域上将直达波信号与多径信号分离开,实现直达波信号的提取。从这个思路出发,可以考虑将混合信号变换到对时延敏感的稀疏域上,由于信号在稀疏域上具有有效能量的数据点较少,直达波信号与多径信号在稀疏域上具有低概率交叠特性,可以想象,最为理想的稀疏变换就是辐射源信号在此稀疏域上表示为一个点的冲激函数,此时,只要该稀疏变换对时延敏感,则直达波与多径的混合信号在此稀疏域上的表示将分别对应于直达波和多径且在稀疏域上相互分离的多个点的冲激函数,则接下来就可以利用滤波方法或参数估计的方法来抑制多径信号或恢复直达波信号,实现直达波信号的提取。本文将从雷达辐射源的信号特性出发,充分利用线性调频信号在分数阶傅里叶变换(Fractional Fourier Transformation,FRFT)域上的稀疏特性,根据变换关系,通过FRFT 域的尖峰参数推导出直达波信号的参数,恢复直达波信号,从而实现直达波信号提纯。

1 问题描述

假定系统是岸基固定的,且参考天线主瓣对准辐射源,则进入参考通道的目标回波信号十分微弱可以忽略。实际情况中,参考通道接收到的辐射源直达波信号伴随着多径干扰信号,如图1所示。假设在所接收到的参考通道中,存在个多径信号,则

图1 参考信号受多径干扰示意图Fig.1 Reference signal interfered by multipath signals

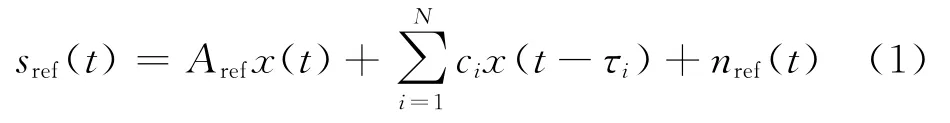
式中：()为参考通道接收信号；()为辐射源直达波信号；是参考通道中直达波信号的复包络；()为参考通道中的噪声；c和τ分别为第个多径信号的复包络和时延,不失一般性,令=1,τ＜τ。

为了进一步分析参考通道中多径信号对目标检测性能的影响,假设有2个强目标和1个弱目标,在距离-多普勒曲面分别位于(19.5 km,50 Hz)、(60.0 km,-83 Hz)和(75.0 km,60 Hz),信噪比分别为-16.9、-18.3和-24.4 dB,监测通道接收信号中除了3 个目标回波外,还包含1个直达波干扰和10个多径干扰。1个直达波干扰的干扰噪声比是62.3 dB,10个多径干扰的干扰噪声比处于(4～34 d B)范围内,仿真场景如图2所示。

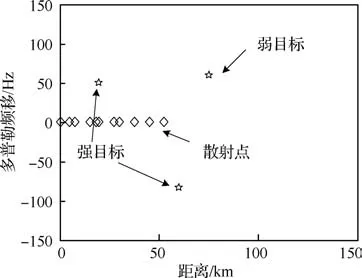
图2 仿真场景Fig.2 Simulation scenario

当参考信号不受多径干扰时,采用文献[22]中的方法,将监测通道接收信号投影到多径干扰的正交补子空间内,消除强直达波与强多径干扰,并进行二维互相关检测,得到的结果如图3所示。从图3中可以看出,利用“纯净”的直达波信号作为参考信号进行监测通道的多径杂波对消和二维互相关检测,3个目标可以很容易被检测到。当参考通道接收信号除了辐射源直达波信号外,还包含10个多径干扰时,直达波与多径杂波功率之比分 别 为2.1、3.2、4.8、6.5、9.2、12.3、11.6、14.9、17.2、19.8 dB,如果直接利用“不纯净”的参考信号进行监测通道的多径杂波对消和二维互相关检测,得到的结果如图4 所示。与图3 相比,2个强目标虽然能够被检测到,但由于参考信号的“不纯净”,不能为多径杂波对消和二维互相关检测提供准确样本,导致强目标产生模糊旁瓣,同时,还出现虚假目标,且弱目标被抑制,很难被检测到。因此,参考通道直达波信号提纯对于系统目标检测性能十分重要。

图3 参考信号不含多径杂波时的互模糊函数Fig.3 Cross correlation function for a reference signal without multipath

图4 参考信号含多径信号时的互模糊函数Fig.4 Cross correlation function for a reference signal with multipath

2 参考信号的稀疏性

从数学角度,分数阶傅里叶变换可被理解为时频平面内坐标轴绕原点逆时针旋转任意角度后构成的表示方法,是传统傅里叶变换的广义形式,可作为信号时频分析的一种方法。

从积分核的角度出发,输入函数()的阶FRFT 定义为

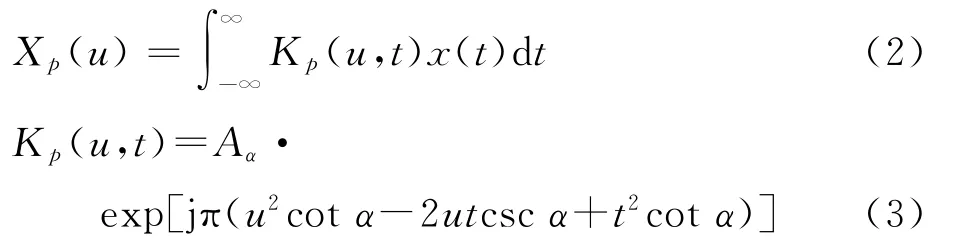
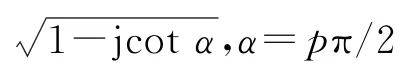
本文以发射LFM 脉冲信号的雷达作为非合作辐射源,非合作无源探测系统参考通道接收的直达波信号可表示为

式中：为直达波信号包络；为起始频率；=/为调频斜率,为信号持续时间,为信号调频带宽。不失一般性,取=0,=1,则信号阶FRFT 为

将式(5)变量代换后简化为

由式(6)可看出,当变换阶次=arccot(-)/(π/2)时,直达波信号在FRFT 域上表现出了良好的能量聚集稀疏特性。也就是说,只要找到与直达波信号能量聚集特性对应的最佳阶次,与之对应的FRFT域的正交基字典就可以被构造出来,在该字典下,直达波信号将满足稀疏性和正交性。FRFT的周期为4,∈(-2,2],对应旋转角度∈(-π,π],由FRFT 的时频旋转特性可知,当变换阶次从0变化到1,即可展示出信号从时域转换到频域的所有特征,根据对称性,只要观察∈(-1,1]就可找到符合条件的最佳变换阶次。

正交基字典矩阵是能否将信号进行稀疏表示的关键,由于直达波信号是在FRFT 基上分解信号的,可考虑用离散分数阶傅里叶变换(Discrete Fractional Fourier Transformation,DFRFT)核矩阵来构成正交字典K ,由上述分析可知,K 能很好地稀疏表示直达波信号,不同的变换阶次对应不同的核变换矩阵。下面将根据DFRFT 核构造出正交基字典K ,并证明直达波信号在K 下的正交性和稀疏性。

考虑直接采样连续分数阶傅里叶变换核来获得DFRFT核矩阵,进一步由离散核矩阵来构造FRFT正交基字典。这类方法中,Pei采样型算法具有计算复杂度最低、运算效率最高等特点,得到了广泛的使用。为了使离散分数阶傅里叶变换具备正交性和可逆性,其对连续分数阶傅里叶变换在分数阶傅里叶域和时域选择合适的采样间隔。本文基于分数阶傅里叶变换的正交基字典构造方法步骤如下：

对输入函数()和输出函数X ()分别以Δ和Δ为采样间隔进行采样,即()=(Δ),Y ()=X (Δ),∈[-,],∈[-,]。

由连续FRFT 定义式(2)可知

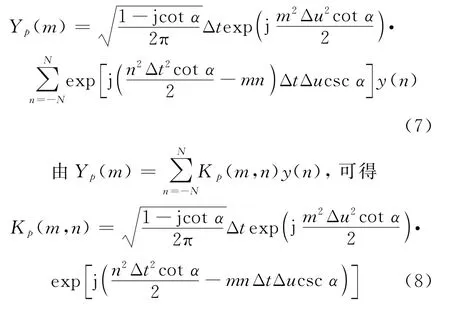
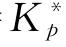
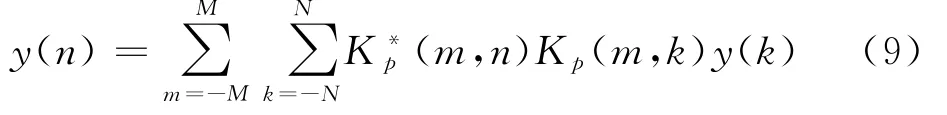
由变换可逆性可知,式(9)对求和等于(-),即

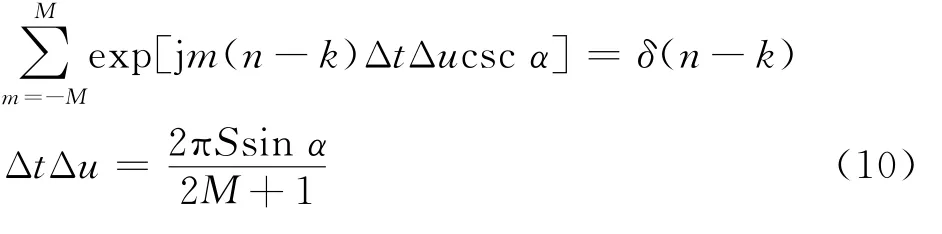
式中：是与2+1互质的整数。

将式(10)代入式(8)归一化得

令=sgn(sin)=±1,当sin＞0时,代入式(11)得

采用正交基字典,令=,就可以得到所要构造的DFRFT 正交基字典

进一步,可以得出利用FRFT 核矩阵构成的字典K 也是参考通道接收信号()的正交基字典,证明详见附录A。

3 参考信号提纯

由第2节的分析可知,通过对参考通道接收信号进行FRFT,可将时域上混叠在一起的直达波信号和多径信号在稀疏域上分离开,通常考虑采用滤波器技术就可将其他多径信号抑制掉。但实际情况中,很难设计出一种理想的滤波器将多径信号完全抑制的同时还能尽可能完整地保留直达波信号,尤其在多径时延很小的情况。因此,本节考虑从FRFT 变换关系出发,由参考通道接收信号在FRFT 域的尖峰参数推导出直达波的参数,重构提纯直达波信号。

由参考通道接收信号模型式(1)和式(3)可知,多径信号需要估计的参数有：调频斜率、多径信号包络c和时延τ,下面给出这些参数的估计。

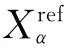
从分数阶傅里叶变换的定义出发进行推导可以得出,直达波信号的包络估计为

得到直达波信号的参数估计后,就可以参考信号提纯

综上所述,基于稀疏特性的直达波参考信号提取方法步骤如下：

连续变化旋转角度或者阶次,对参考通道接收信号()进行分数阶傅里叶变换,形成参考通道接收信号的能量在(,)平面上的三维分布图。

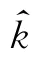
利用步骤3中估计出的直达波信号参数,根据式(17)实现直达波信号提纯。

4 仿真实验与分析

为了验证基于稀疏特性的直达波信号提纯算法的有效性,进行相应的仿真实验。对雷达辐射源LFM 直达波信号仿真参数设置如下：信号带宽=5 MHz,观测时长=8μs,LFM 信号的调频斜率=/=6.25×10Hz/s,信号采样频率=100 MHz,采样间隔=1/=10s,信号采样点数为800,信号归一化幅度为1,信噪比SNR=8 dB的直达波信号如图5所示。用不同的延时=1μs和=2μs以及对应的幅度=05和=08来模拟2条多径信号,参考通道中直达波与多径信号的混合信号如图6所示。

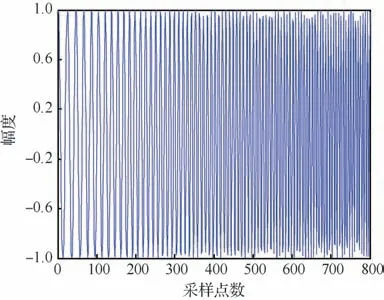
图5 直达波信号(SNR=8 dB)Fig.5 Direct signal(SNR=8 dB)

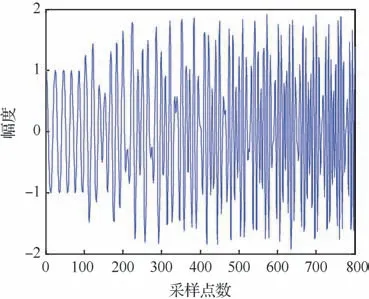
图6 参考通道接收的混合信号Fig.6 Mixture of direct signal and multipath signals received by reference channel

图7 参考通道接收信号的FRFT 三维图Fig.7 3D plot of FRFT of the received signal in reference channel

图8 DFRFT 字典矩阵Fig.8 Dictionary matrix of DFRFT

图9 参考通道接收信号在最佳旋转角度下的FRFTFig.9 FRFT of received signal in reference channel with the best rotation angle

从分数阶傅里叶变换与输入信号的对应关系出发,根据第3节中的参数估计方法消除多径信号,实现参考信号提纯后,参考通道接收信号的FRFT 三维图和在最佳旋转角度下的FRFT 如图10和图11所示。不难看出,参考通道接收信号中的多径信号得到了很好地抑制,直达波信号得到了很好地保留,提取出的直达波波形与纯净的直达波波形十分接近,如图12所示。

图10 参考通道接收信号的FRFT 三维图(多径信号消除后)Fig.10 3D plot of FRFT of received signal in reference channel after multipath removal

图11 参考通道接收信号在最佳旋转角度下的FRFT(多径信号消除后)Fig.11 FRFT of received signal in reference channel with the best rotation angle after multipath removal

图12 多径信号消除后的直达波信号Fig.12 Direct signal after multipath removal

为了进一步定量评价本文方法参考信号提纯的性能,定义波形失真率为

式中：()为纯净的直达波信号；()为提取的直达波信号,波形失真率表示提取的直达波信号与纯净的直达波信号之间的相似程度。同时,与需要采用多通道接收机的空域自适应滤波方法相比,本文算法可适用于单通道接收机,无需增加接收机硬件复杂度,故将本文方法与时域自适应滤波方法进行仿真性能对比,图13给出了不同信噪比下2 种方法提取的直达波信号波形失真率。可以看出,本文方法提纯信号的波形失真率比时域自适应滤波方法要小,直达波参考信号提纯效果更好。随着信噪比的增大,采用本文方法提取的直达波信号波形失真率在不断减小,提取的直达波信号精度越高。这是由于随着信噪比的增大,参数估计的精度会提高,字典的稀疏表达能力越强,多径信号的参数估计精度也越高,因此提取的直达波信号波形失真率减小,直达波信号提纯效果越好。

图13 不同信噪比下2种方法的波形失真率Fig.13 Waveform Distortion rate of the two methods with different SNRs

由于非合作无源探测中的目标检测是在参考信号与监测信号进行匹配滤波的基础之上进行的,波形失真率越低,参考信号提纯效果越好,则匹配滤波获得的目标信号增益越大,越有利于目标检测。因此,匹配滤波后的目标信号峰值信噪比可衡量目标检测性能的好坏。为便于分析,假定有一个目标距离为15 km 的固定目标,图14和图15分别给出了波形失真率分别为62%和28%时,提纯的参考信号与目标信号进行匹配滤波的结果。从图中不难看出,当波形失真率越低,参考信号提纯效果越好,匹配滤波获得的目标信号增益越高,目标信号信噪比就越高,目标就越容易被检测出来。

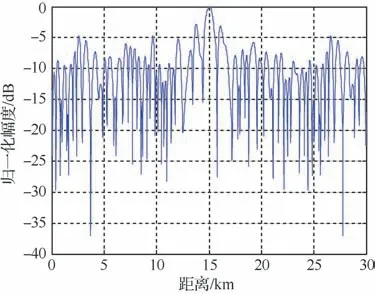
图14 波形失真率为62%时匹配滤波输出Fig.14 Output of match filter of waveform distortion rate of 62%

图15 波形失真率为28%时匹配滤波输出Fig.15 Output of match filter of waveform distortion rate of 28%

5 总 结

针对非合作无源探测中的参考信号提纯问题,本文以发射线性调频脉冲信号的雷达作为非合作辐射源,提出了一种基于稀疏特性的参考信号提纯新方法。仿真实验结果表明,本文方法能够充分利用LFM 信号在分数阶傅里叶变换域上的稀疏特性,将直达波信号与多径信号在稀疏域上分离,通过参数估计实现参考信号有效提纯,且与时域自适应滤波方法相比,提纯的直达波参考信号失真更小。虽然,本文方法主要适用于基于LFM 脉冲雷达辐射源的非合作无源探测系统,但本文方法的技术思路仍可参考借鉴应用于利用其他辐射源信号的系统,关键是寻找到合适的稀疏域。

利用FRFT 核矩阵构成的字典K 是参考通道接收信号()的正交基字典。

证明 本命题可分解为2个子命题：①证明字典K 是正交字典；②证明多径信号在K 上是稀疏的。

1)根据FRFT 定义式,K 是由一组Chirp信号展开成的满足正交条件的完备正交基,在离散核矩阵来构造FRFT 正交基字典过程中,各个基函数之间相互正交。

2)令参考通道接收信号中直达波信号FRFT 为X (),当变换阶次满足=arccot(-)/(π/2)时,大小为(),具有稀疏性。

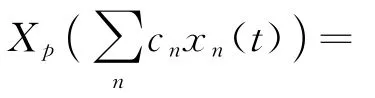
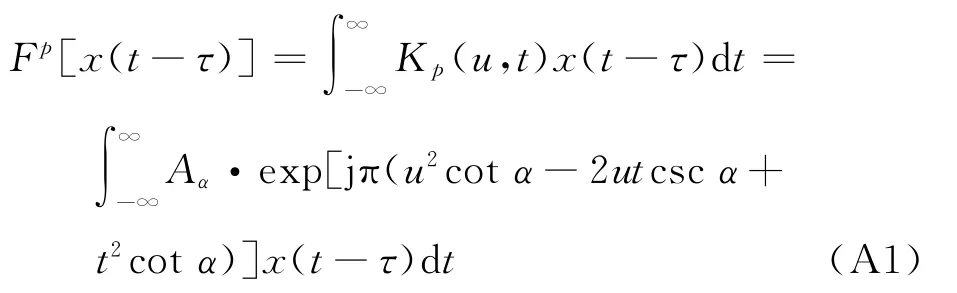
令=-,=-cos代入式(A1)得

式(A2)化简可得

令=-cos,换元后可得

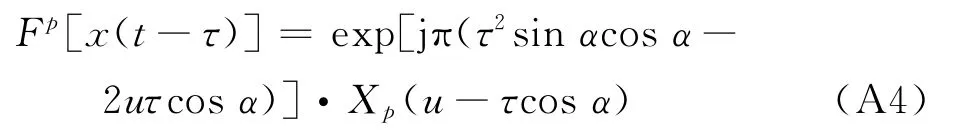
可以看出,多径信号的FRFT 与X ()只存在着不同的相移和时移因子,且同一阶数下FRFT 将具有相同的模。

选取最佳阶次=arccot(-)/(π/2),=π/2,有X ()=(),则F [(-)]是一个经过一定时移和相移后的冲激函数,且域时移与域时延对应关系为=cos,也具有稀疏性,证明完毕。