基于快速迭代收缩阈值算法识别移动荷载

孙梦晴

摘 要：在桥梁设计规范中，移动力对活载构件起着重要的作用。然而，由于移动力的变化是在时间和空间上同时发生的，很难直接测量车辆和桥梁之间的相互作用力。因此，开发一些间接鉴定方法是有益的。间接法是根据已知桥梁动力特性和实测的实际动力响应计算动力。与直接法的成本相比，间接法的成本较低。考虑一类迭代收缩阈值算法（ISTA）来解决信号中出现的线性逆问题。這类方法可以看作经典梯度算法的扩展，因其简单而便捷，足以解决大规模问题以及有密集的矩阵数据，但这类方法收敛速度也很慢。本研究提出了一种新的快速迭代收缩阈值算法，FISTA算法保持了ISTA算法的计算简单性，且具有全局收敛速度快的优势，在理论和实践上都得到了显著的改善。

关键词：快速迭代收缩阈值;函数值;迭代速度

中图分类号：TP391     文献标志码：A     文章编号：1003-5168（2022）3-0014-04

DOI：10.19968/j.cnki.hnkj.1003-5168.2022.03.003

Moving Load Identification Based on Fast Iterative Shrinkage Threshold Algorithm

SUN Mengqing

（School of Civil Engineering and Communication， North China University of Water Resources and Electric Power， Zhengzhou 450045，China）

Abstract：In the bridge design code， the displacement force plays an important role in the live load components.However， it is difficult to measure the interaction force between the vehicle and the bridge directly because the variation of the displacement force occurs simultaneously in time and space.Therefore， it would be beneficial to develop some indirect identification methods.The indirect method is based on the known dynamic characteristics of the bridge and the measured actual dynamic response to calculate the force.The cost of the indirect method is lower than that of the direct method.We consider a class of Iterative Shrink Threshold Algorithm （ISTA） to solve the linear inverse problem occurring in the signal.This type of method can be seen as an extension of the classical gradient algorithm， because it is simple and convenient enough to solve large-scale problems， even with dense matrix data.However， this kind of method also converges slowly.In this study， a new fast iterative shrinkage threshold algorithm， FISTA algorithm， maintains the computation simplicity of ISTA algorithm and has the advantage of fast global convergence， which has been improved significantly both in theory and practice.

Keywords：fast iterative shrinkage threshold; function value;iteration speed

0 引言

ISTA算法和FISTA算法都是求解线性逆问题的经典方法，属于梯度类算法。FISTA是一种简单而有前景的迭代方式，甚至比已证实的理论预测速度更快。分析是验证全局收敛速度和效率的方法，如ISTA和FISTA通过函数值测量进行比较，来说明算法收敛速度的有效性。

值得注意的是，动态力重构问题已经得到了广泛的研究，并提出了许多有效的方法。近年来，随着计算理论的发展和新型方法的出现，为了提高载荷识别的稳定性和准确性，许多研究者都在这一问题上做了大量的研究工作。移动荷载识别理论在过去的几十年里得到了长足的发展，并提出了许多有效的方法。Yu等[1]对四种基本的MFI方法，即解释方法Ⅰ（IMⅠ）、解释方法Ⅱ（IMⅡ）、时域方法（TDM）[2]和频时域方法（FTDM）[3]进行了全面研究。Wu等[4]提出了一种基于统计系统模型的MFI技术。根据叠加原理和影响面概念，Deng等[5]提出了一种用于车辆轴载估计的MFI方法。Bao等[6]采用L1范数正则化方法求解斜拉桥上移动重型车辆荷载的分布。稀疏正则化最大的优点是解决了特征提取问题。

作为第二类反问题，MFI问题是一个典型的不适定问题，即解的存在性、唯一性和稳定性中至少有一点不能满足。因此，离散的移动识别方程总是病态的，识别结果对噪声敏感。正则化方法广泛应用于改善这一缺陷，如基函数法（BFM）、Tikhonov正则化方法、稀疏正则化方法等。必须强调的是，现有的BFM总是使用单类基函数集。然而，在实际工程中，车桥耦合系统的运动力是非常复杂的。它们不仅包括整个时间历史中缓慢变化的谐波分量，还包括局部影响分量。因此，仅用一类基函数集很难完整、稀疏地表达运动力。这是现有的针对动力识别问题的BFMs的主要缺点。经典的Tikhonov正则化方法是最著名的正则化技术之一，在移动荷载识别中已经得到充分的研究[7-8]。在大多数情况下，经典Tikhonov正则化方法的解可以通过奇异值分解（SVD）以一种特殊的方式进行分析。基于奇异值分解方法最大的优点是可以将复杂的问题解耦为简单的问题。Rezayat等[9]提出了一种基于群稀疏性的方法来识别动态力的未知时间和未知位置。以上方法都是针对固定位置的力重建。Bao等[6]采用L1范数正则化方法求解斜拉桥上移动重型车辆荷载的分布，但笔者仅研究静力。稀疏正则化最大的优点是解决了特征提取问题。作为一个凸优化问题，L1范数正则化是最常用的稀疏正则化方法之一。

1 介绍

ISTA的收敛性分析已经在各种语境和框架下，包括各种修改的文献中得到了很好的研究，重点建立序列{X}收敛于式（1）解的条件。ISTA的优点在于它的简单性。然而，ISTA也被认为是一种缓慢的方法。由ISTA算法生成的序列x的收敛速度为O（1/K），显然为次线性收敛速度。笔者关注的是非渐近的全局收敛速度和效率的方法，如ISTA通过函数值测量。本研究将考虑更一般的非光滑凸优化模型。

其中，G（·）为式（1）中LS（最小二乘）项的梯度步长，ISTA是经典梯度法的扩展。因此，ISTA属于一类一阶方法，即基于函数值和梯度求值的优化方法。众所周知，对于大规模问题，一阶方法通常是唯一可行的选择，已经观察到序列{X}收敛到一个解相当缓慢。作为第一个结果，通过证明ISTA的行为来进一步确认这个属性。

即共享一个次线性的全局收敛速度。

重点是是否可以设计一种比上面描述的迭代收缩阈值方案更快的方法，新方法的计算工作量将ISTA简单化，而其全局收敛速度将会更好地在理论上实践。FISTA与ISTA的不同之处在于每一步迭代时近似函数起始点的选择。为了实现这个目标，考虑一种类似于ISTA的方法x=T[G（x）]，新点y会被巧妙地选择。它是由Nesterov在对求光滑凸函数的最小化，并证明了在复杂度分析意义上是“最优”的一阶（梯度）方法。

在这里，考虑的问题是凸的，但不是光滑的，因为有L1项。尽管在目标函数中存在非光滑正则化，证明可以构造一个比ISTA更快的算法，称为FISTA，它保持了ISIA算法的简单性，为最小化光滑凸问题而设计的最优梯度方法的改进速度O（1/K）。理论分析是一般性的，可以处理具有任意凸非光滑正则化的目标函数（超出L）和任意光滑凸函数，也可以处理约束。

迭代收缩算法的基本思想是在每次迭代时对目标的线性化可微函数部分建立正则化。为了便于分析，考虑一般公式（4），它自然地扩展了公式（1）。

提出了以下假设：

·g：R→R是一个可能是非光滑的连续凸函数。

·f：R→R是一类光滑凸函数C，，即连续可微的Lipschitz连续梯度L（f）：‖∇f（x）−∇f（y）‖≤L（f）‖x-y‖。对于每一个x，y∈R，其中‖·‖为标准欧几里得范数，L（f）>0为∇f的Lipschitz常数。

·问题（P）是可解的，即X∗=argminF≠ϕ，x∈X设F=F（x）。

2 一种快速迭代收缩阈值算法

一般模型由最小化平滑凸函数和ISTA简化为梯度法组成。在这种光滑条件下，存在一个O（1/K）复杂度的梯度方法，这是光滑问题的“最优”一阶方法。值得注意的是，在已知方法不需要在每次迭代中进行一次以上的梯度计算（也就是说，与梯度方法相同），只需巧妙地选择一个易于计算的额外点。MFI采用了1/4跨（1/4 m）的弯矩响应和1/2跨（1/2 a）的加速度响应，并建立改进的复杂度结果。

用一个恒定的步长表示算法。

FISTA的固定步长

输入：L=L（f）-A的李普希茨常数∇f。

开始：让[y1]=[x0]∈Rn，[t1]=1。

第k步：（k≥1）计算

[Xk]=PL[（yk）]       （5）

[tk+1]=[1+1+4t2k2]      （6）

[yk+1]=[Xk]+（[tk−1tk+1]）（[Xk]-[Xk+1]）    （7）

上述算法和ISTA的主要區别是迭代收缩算子PL（·）不使用以前的点X，而是在[yk]使用一个非常具体的线性组合前面两点{X，X}。显然，ISTA和FISTA的主要计算工作量是相同的，即在算子PL中。式（6）和式（7）中对FISTA要求的额外计算显然是边际的。

本研究還将使用回溯步长规则来分析FISTA，现在将显式地说明这一点。

FISTA与回溯

为了加速ISTA算法的收敛，采用了梯度加速策略Nesterov加速技术，使得ISTA算法的收敛速度从O（1/K）变成O（1/K）。FISTA与ISTA算法相比，仅仅多了个Nesterov加速步骤，以极少的额外计算量大幅提高了算法的收敛速度。

3 数值模拟

为了证明FISTA算法的正确性和有效性，决定采用FISTA算法改进的时域法进行移动荷载识别。数值仿真采用的桥梁参数如下：梁长L=40 m，梁密ρ=12 000 kg/m，梁抗弯刚度EI=1.279 14×10 N·m;车辆车轴轴距l=8 m，车速c=40 m/s。桥梁前四阶段固有频率为：f=3.2 Hz，f=12.8 Hz，f=28.8 Hz，f=51.2 Hz。分析频段在0～50 Hz，采样频率取为200 Hz。本研究以伯努利欧拉简支梁作为桥梁的计算模型，通过桥梁动力响应组合进行移动荷载识别。所有仿真过程通过MATLAB计算软件及工具箱实现。设置一种桥上移动荷载，如下所示。

两轴时变移动荷载一：

针对两轴移动荷载作用情况，将FISTA的性能与基本的ISTA算法进行比较。由于模拟时考虑的是极端病态问题，所有的方法都是使用一个常数步长规则，并应用于L正则化中f（x）=‖Ax−b‖和g（x）=λ‖x‖。在进行的所有模拟中，观察到FISTA在达到给定精度所需的迭代次数方面明显优于形成的ISTA。

4 总结

FISTA的功能值始终低于ISTA功能值。还计算了ISTA和FISTA在1 000次迭代后产生的函数值，分别为1.93×10、0.9×10。需要注意的是，ISTA经过1 000次迭代后的函数值仍然比FISTA经过500次迭代后的函数值差。

在本例中，将进一步展示FISTA的优势。采用正则化参数λ=2×10对算法进行了测试，描述了迭代100和200次的结果，很明显FISTA提供更好改进的功能值。此外，函数值FISTA迭代100次得到的0.009 9优于第200次迭代时的ISTA方法函数值0.009 7。此外，ISTA需要195次迭代才能达到FISTA经过100次迭代得到的值（0.009 9），需要400次迭代才能达到FISTA经过200次迭代得到的值0.004 9。

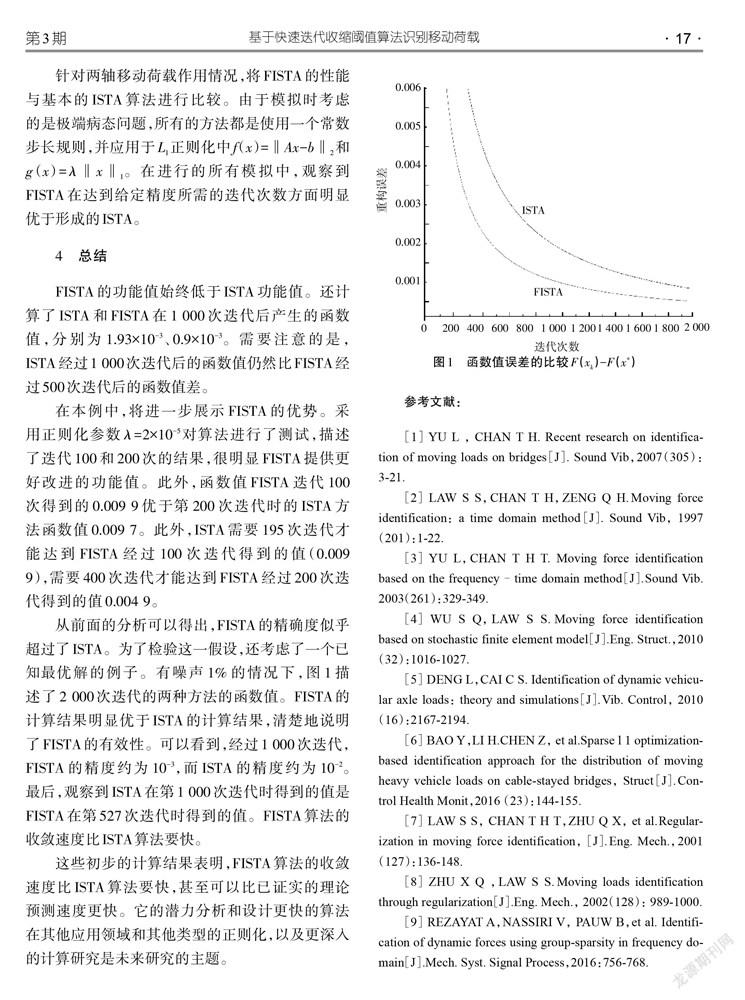
从前面的分析可以得出，FISTA的精确度似乎超过了ISTA。为了检验这一假设，还考虑了一个已知最优解的例子。有噪声1%的情况下，图1描述了2 000次迭代的两种方法的函数值。FISTA的计算结果明显优于ISTA的计算结果，清楚地说明了FISTA的有效性。可以看到，经过1 000次迭代，FISTA的精度约为10，而ISTA的精度约为10。最后，观察到ISTA在第1 000次迭代时得到的值是FISTA在第527次迭代时得到的值。FISTA算法的收敛速度比ISTA算法要快。

这些初步的计算结果表明，FISTA算法的收敛速度比ISTA算法要快，甚至可以比已证实的理论预测速度更快。它的潜力分析和设计更快的算法在其他应用领域和其他类型的正则化，以及更深入的计算研究是未来研究的主题。

参考文献：

[1] YU L ， CHAN T H. Recent research on identification of moving loads on bridges[J]. Sound Vib，2007（305）：3-21.

[2] LAW S S，CHAN T H，ZENG Q H.Moving force identification： a time domain method[J]. Sound Vib， 1997（201）：1-22.

[3] YU L，CHAN T H T. Moving force identification based on the frequency–time domain method[J].Sound Vib. 2003（261）：329-349.

[4] WU S Q，LAW S S.Moving force identification based on stochastic finite element model[J].Eng. Struct.，2010 （32）：1016-1027.

[5] DENG L，CAI C S. Identification of dynamic vehicular axle loads： theory and simulations[J].Vib. Control， 2010 （16）：2167-2194.

[6] BAO Y，LI H.CHEN Z， et al.Sparse l 1 optimization-based identification approach for the distribution of moving heavy vehicle loads on cable-stayed bridges， Struct[J].Control Health Monit，2016 （23）：144-155.

[7] LAW S S， CHAN T H T，ZHU Q X， et al.Regularization in moving force identification， [J].Eng. Mech.，2001 （127）：136-148.

[8] ZHU X Q ，LAW S S.Moving loads identification through regularization[J].Eng. Mech.， 2002（128）： 989-1000.