基于G-RRT*算法的煤矸石分拣机器人路径规划

朱子祺，李创业，代伟

（1.国家能源集团神东煤炭集团公司 洗选中心,陕西 榆林 719300；2.郑州机电工程研究所,河南 郑州 450015；3.中国矿业大学 信息与控制工程学院,江苏 徐州 221116）

0 引言

我国能源资源的特点是富煤、贫油、少气，在已探明的一次能源储量中，煤炭占85%以上，煤炭在我国经济发展中具有重大战略意义[1-3]。煤矸石是在煤炭开采时产生的一种固体废料，煤矸石分拣是煤炭生产过程中不可或缺的环节，对于提高煤炭质量及企业收益具有重要意义[4-5]。传统的人工选矸方式存在劳动强度大、生产效率低的缺点，恶劣的工作环境使得工伤事件频发[6-8]。随着机器人技术的发展，利用机器人分拣煤矸石逐渐成为研究热点[9-11]。由于煤矸石分拣环境复杂，为了避免机器人与障碍物发生碰撞，提高分拣效率，对机器人进行路径规划十分必要[12-14]。

目前用于机器人路径规划的算法主要分为3 类：基于图论的路径规划算法，基于生物启发式的路径规划算法，基于离散采样的路径规划算法。基于图论的路径规划算法主要有A*算法[15]、D*算法[16]，该类算法需要精确定位障碍物，且计算量过大，耗时长，因此实用性不强。基于生物启发式的路径规划算法主要有遗传算法[17]、粒子群优化算法[18]，该类算法大多需要经过多次重复训练来确定算法参数，计算量大，搜索时间长，且运行时需要占用大量存储空间。基于离散采样的路径规划算法的主要思想是在配置空间中选择有限数量的点，并在这些点之间建立连接，该类算法的复杂度不依赖于地图的复杂度，且具有概率完备性，因此具有较强实用性。

快速扩展随机树（Rapidly-exploring Random Trees,RRT）作为一种经典的基于随机采样的路径规划算法，具有便捷高效、易于约束、概率完备等特性，比较适用于高维空间中的路径规划。但RRT 算法是在给定搜索空间内进行全局随机采样，具有极大的盲目性，易在无效空间内进行过多采样，耗费较大计算代价。而用于煤矸石分拣的机器人需要尽可能地缩短任务周期，因此，应尽量规划出较短路径。

RRT*算法[19]在RRT 算法基础上进行了改进，每次扩展时选取新节点附近的节点中与起始点距离最近的点作为父节点，确保随机树的节点都能收敛到当前最优值。RRT*算法虽然具有路径长度渐进最优的特点，但仍存在盲目搜索的问题。为了提高搜索效率，一般的方法是引入目标偏置策略，而传统目标偏置策略的概率值是固定的，无法根据实际环境进行调整，造成对可行空间进行无必要的搜索且会使路径不够平直。针对该问题，本文提出一种变概率的目标偏置策略，该策略在无障碍物区域增大目标偏置概率值以增强算法的目标导向性，而在障碍物区域减小目标偏置概率值以保证算法的避障能力；提出G-RRT*（Goal-RRT*）算法，将变概率的目标偏置策略与RRT*算法相结合，既保留了RRT*算法路径长度渐进最优的特点，也提高了算法的目标导向性。

1 煤矸石分拣机器人路径规划问题描述

煤矸石分拣系统主要由上位机、煤矸石识别子系统、机器人、输送带测速装置等组成，通过TCP/IP通信协议实现连接，如图1 所示。煤矸石识别子系统用于分辨煤和矸石，将矸石位置信息打包发送给上位机；上位机结合矸石位置信息和测速装置反馈的输送带速度信息，计算出矸石到达抓取点的时间，给机器人下发抓取任务；机器人根据上位机分配的任务抓取矸石并送到指定位置，完成煤矸石分拣。

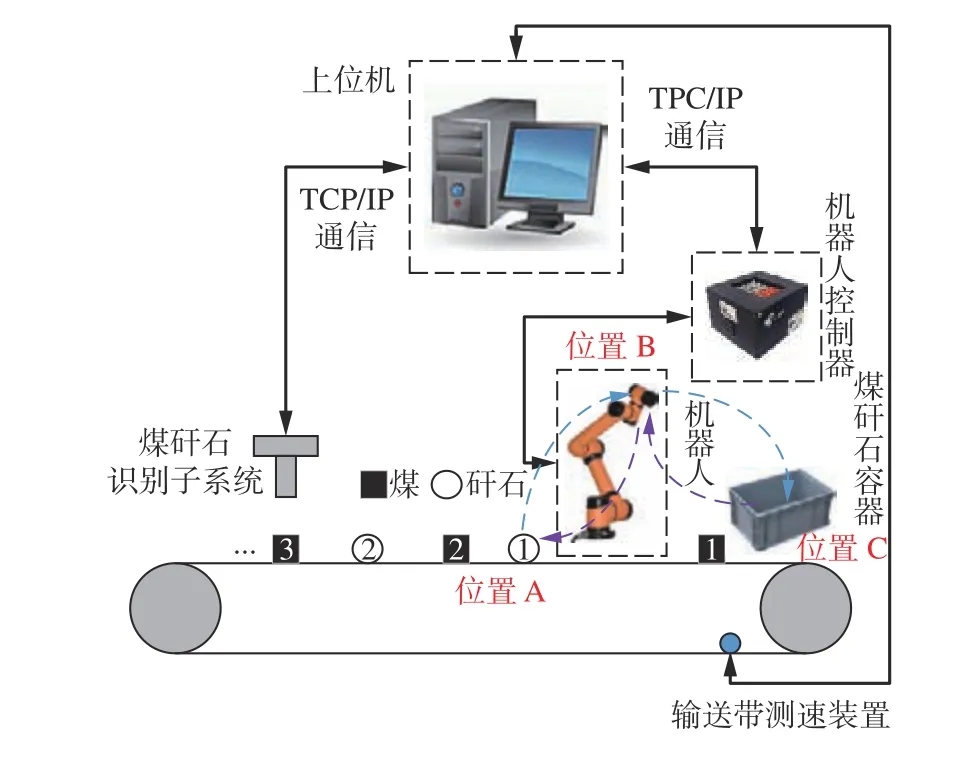
图1 煤矸石分拣系统Fig.1 Coal gangue sorting system

在煤矸石分拣过程中，输送带是一直运动的，即煤矸石识别子系统识别到矸石后，矸石继续向前运动。因此，在目标矸石到达机器人的可行工作区间之前，机器人应完成上一次的分拣任务并提前回到初始位置，准备抓取目标矸石。

煤矸石分拣机器人路径规划问题可归结为在障碍物环境下规划出一条从给定起点到目标点的无碰撞路径。煤矸石分拣机器人路径规划需要满足以下条件：

（1）速度快：规划的路径应尽可能短，使得机器人执行任务的时间尽可能小于2 个抓取任务的时间间隔。

（2）约束性：路径规划算法要满足工作环境的约束。输送带作为煤和矸石的载体，给路径规划算法增加了位置约束，即机器人在运动过程中要避免与输送带和其他障碍物接触。

本文主要针对煤矸石分拣机器人路径规划算法部分进行研究，因此，针对煤矸石分拣系统的其他部分作如下假设：

（1）煤矸石识别子系统能够提供精确的矸石位置和对应的机器人关节角度值。

（2）输送带测速装置能够实时反馈输送带的速度、加速度。

（3）煤矸石识别子系统识别出矸石位置后，矸石相对于输送带的位置不再发生变化。

（4）使用球形或方形包络体代替障碍物，使用圆柱体代替机器人连杆，使用球体代替机器人末端执行器。

2 煤矸石分拣机器人路径规划方案设计

机器人路径规划一般在笛卡尔空间或关节空间中进行。笛卡尔空间即三维空间，在该空间进行路径规划的优点是障碍物容易表达、空间维度低，缺点是需要通过求逆解得到关节路径，但求机器人的逆解计算量大且解一般不唯一。关节空间即驱动机器人运动的关节角空间，在该空间中进行路径规划的优点是规划出的路径即为机器人能够直接运行的路径，缺点是需将障碍物从笛卡尔空间映射到关节空间，技术难度较大。本文结合笛卡尔空间和关节空间的优点，提出一种在关节空间进行路径规划、在笛卡尔空间进行碰撞检测的方案，该方案不需要对机器人进行运动学求逆，且可避免在关节空间中描述障碍物。

机器人路径规划方案分为机器人建模、路径规划算法、任务空间转换及碰撞检测4 个模块，如图2所示。

图2 机器人路径规划方案Fig.2 Robot path planning scheme

要实现机器人路径规划，首先要针对机器人的机械结构进行建模。本文选用AUBO-i5 机器人，其结构如图3 所示。采用D-H 参数法对机器人进行建模。根据实物机器人结构尺寸，得到机器人的D-H 参数，根据D-H 参数可推导出基坐标系到各关节坐标系的转换关系，进而得到末端执行器的位姿矩阵。

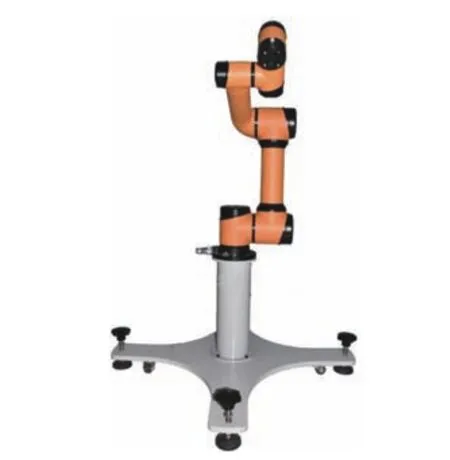
图3 机器人机械结构Fig.3 Robot mechanical structure

实际煤矸石分选环境中的机器人和障碍物都是不规则物体，很难假定它们之间的碰撞条件，因此，简化机器人连杆和障碍物模型对于提高碰撞检测效率具有重要意义。根据机器人连杆结构和障碍物特点，将连杆简化为圆柱体，将障碍物简化为球体或长方体，如图4 所示。机器人与障碍物之间的碰撞检测问题转换为一系列判断规则几何体之间是否交涉的问题。

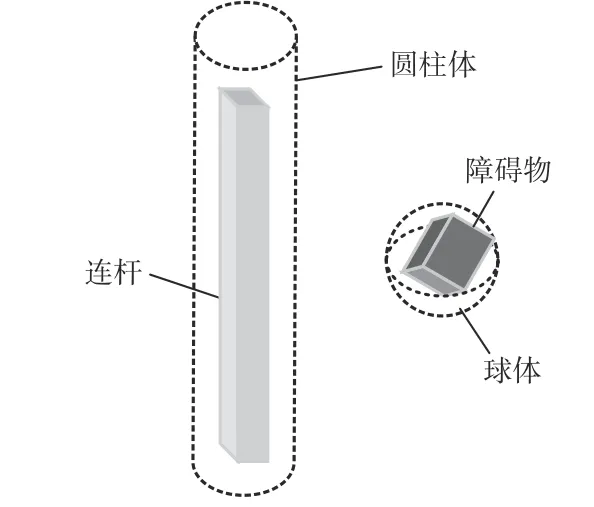
图4 机器人连杆和障碍物简化模型Fig.4 Simplified model of robot link and obstacle

3 路径规划算法

3.1 RRT 算法原理

RRT 算法是一种类似于树生长的空间搜索算法。从给定起点xinit开始进行扩展搜索，并将搜索节点存储于一个树状结构（随机树）中，如图5 所示。扩展新节点时，通过在可行空间中随机采样获取采样点xsample；在随机树中寻找距离采样点xsample欧氏距离最近的点作为最近节点xnearest，并以一定步长s生成新节点xnew；判断xnew是否处于障碍物中，若是则舍弃该节点，重新进行采样，反之则将xnew加入随机树中；如此循环搜索，直至到达目标点xgoal。

图5 RRT 算法节点扩展Fig.5 Node extension of RRT algorithm

RRT 算法在给定空间中进行全空间的盲目随机采样，搜索效率较低，且得到的路径一般不是最优路径，不能满足机器人路径规划要求。

3.2 RRT*算法原理

RRT*算法由RRT 算法改进而来，是一种路径长度渐进最优的算法，其节点扩展如图6 所示。生成新节点xnew后，以xnew为圆心、一定长度r为半径画圆，得到xnew周围的节点xnear1，xnear2；分别以xnearest，xnear1，xnear2为xnew的父节点，计算3 条路径的长度并选出一条从xinit到xnew的最短路径，图6 中以xnear2为父节点的路径最短，因此用xnear2替换xnearest作为xnew的父节点。按照上述策略进行扩展，保证了RRT*算法路径长度的渐进最优性，但仍不能解决RRT 算法盲目搜索导致效率低的问题，即虽然RRT*算法能够实现最优解收敛，但收敛速度缓慢。

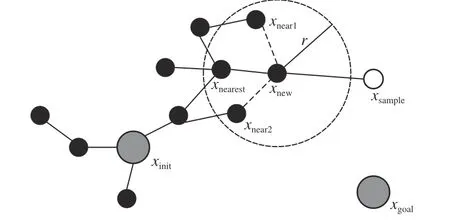
图6 RRT*算法节点扩展Fig.6 Node extension of RRT* algorithm

3.3 目标偏置策略

3.3.1 固定概率的目标偏置策略

为了解决RRT*算法缺乏目标性的问题，对RRT*算法的样本函数进行改进。传统RRT*算法在整个空间中随机选取样本，其延伸方向是全方位的。如果不使用整个空间的样本，而是有目标地选择样本，则可以决定RRT*搜索树的扩展方向。

为了使节点扩展具有一定方向性，设定一个概率值p，使采样点以概率p等于目标点，引导节点向目标点搜索[20-21]。目标偏置策略具体实现过程：首先生成一个随机数rand，判断rand 与概率值p的大小，若rand≤p则直接令采样点等于目标点，不再进行随机采样，否则进行随机采样。目标偏置策略使得RRT*算法具有一定的目标导向性，同时，以1-p的随机概率进行采样，使RRT*算法具有一定避障性能。p值的选取会影响搜索过程和结果，当环境的障碍物密集时应使p值较小，保持算法对未知空间的探索能力，反之应使p值较大，增强算法的目标导向性。

3.3.2 变概率的目标偏置策略

目标偏置策略可以有效地将随机树向目标点引导，但在传统的目标偏置策略中，目标偏置概率值是在算法执行前设定的，不能根据当前节点所处环境进行调整。当目标点与当前节点之间没有障碍物时，若进行大概率的随机采样，会造成不必要的曲折路径；此外，当目标点与当前节点之间有障碍物且当前节点在障碍物附近时，若使采样点等于目标点并引导新节点向目标点扩展，势必会造成新节点与障碍物发生碰撞。

为了避免产生不必要的曲折路径及与障碍物的碰撞，本文提出了一种变概率的目标偏置策略：设置目标偏置概率的初始值为p0，在向目标方向扩展时，如果新节点与障碍物没有发生碰撞，则使目标偏置概率值逐步变大，以增强在目标方向上的搜索能力；如果新节点与障碍物发生碰撞，则需要进行避障，应减小目标偏置概率值，使目标偏置概率值重新等于p0，以增强随机采样能力，避开障碍物。根据多次实验结果，目标偏置概率增加值padd取0.1 时效果较好。

固定概率和变概率的目标偏置策略效果对比如图7 所示。相比于图7（a），图7（b）在目标方向上搜索时树枝更少，且路径更为平直，靠近障碍物时随机树的树枝也能够发散开，以避开障碍物。相比于固定概率的目标偏置策略，变概率的目标偏置策略能够在保证算法避障性能的前提下，提高算法的目标导向性，避免对可行空间的非必要搜索。

当前，农产品质量追溯功能实现的关键环节包括信息采集、信息传递、信息载体和信息查询4个方面。信息采集是实现追溯的基础，农产品质量追溯需要采集的信息主要包括农产品个体（批次）信息、生产过程信息、投入品使用信息、生产者信息、产地信息等[6]。当农产品在市场上流通时，上游生产经营主体采集到的信息还需要准确无误传递到下游生产经营主体，实现信息传递和交换的无缝对接。否则，任何一个环节断了，整个链条就断了，也就无法实现追溯。在信息传递过程中，需要有信息载体来承载所采集到的信息，以便于信息在各个主体之间的传递和交换，追溯功能的实现还需要公共信息平台，便于农产品质量信息汇集和查询。

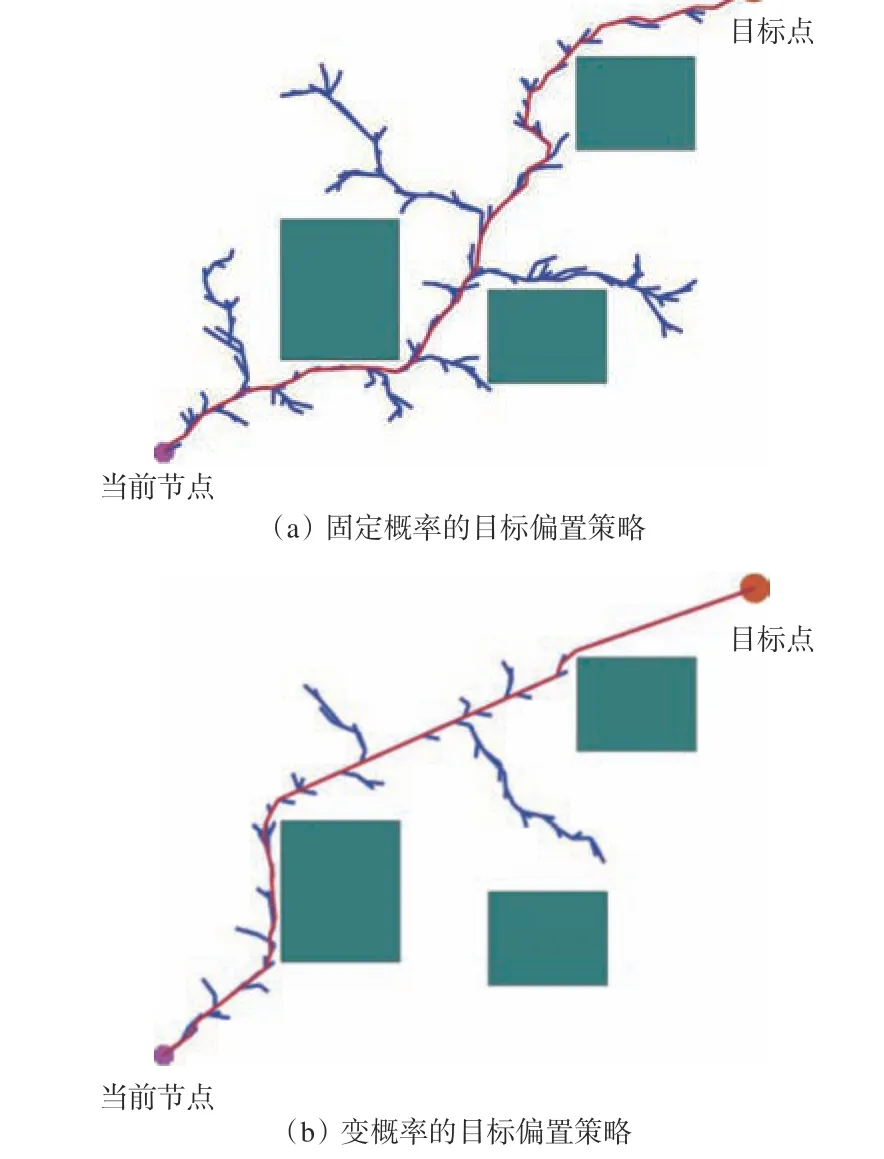
图7 目标偏置策略效果对比Fig.7 Comparison of target bias strategy effects

3.4 G-RRT*算法实现

将变概率的目标偏置策略引入RRT*算法中，得到G-RRT*算法。给定路径起点xinit和目标点xgoal，设置步长为s，目标偏置概率为p，允许误差为E，随机树为T，G-RRT*算法步骤如下：

（1）初始化随机树T，将起点xinit加入T中。

（2）生成一个（0,1）的随机数rand，比较rand 与偏置概率p的大小。如果rand≤p，则令采样点xsample=xgoal；否则在可行空间中进行随机采样，得到采样点xsample。

（3）在T中选择距离采样点xsample最近的点作为最近节点xnearest。

（4）以步长s在xnearest与xsample连线方向上扩展新节点xnew。

（5）以xnew为圆心、r为半径画圆，统计该圆中的节点集合，并判断节点集合中是否存在路径长度小于当前路径长度的节点，若存在则将该节点作为父节点并进行碰撞检测。

（7）判断xnew与xgoal之间的距离是否小于等于误差E。若是则停止搜索，并将目标点加入T中，否则重复步骤（2）-步骤（6），直到满足条件。

（8）回溯父子关系，得到规划路径。

上述过程为G-RRT*算法的一般实现过程，而在机器人上应用时，路径规划是在关节空间中进行的，而障碍物处于笛卡尔空间中，因此，进行碰撞检测时需要将得到的新节点从关节空间转换到笛卡尔空间中，即通过机器人正运动学求出机器人位姿，再执行机器人各连杆与障碍物的碰撞检测。

4 实验验证

为验证G-RRT*算法的避障和路径搜索能力，在Matlab 环境中搭建煤矸石分拣机器人实验场景。根据实际机器人运行需求设置相关参数：机器人每个关节角的运动范围均为（-35π/36，35π/36）；输送带宽度为0.8 m，运行速度为0.6 m/s；矸石粒度为0.1～0.3 m；以矸石储放处为分拣机器人位姿起点，矸石正上方0.5 m 处某点为位姿终点，对应的关节角分别为（-5π/9，7π/18，5π/18，3π/20，0，0）和（π/18，π/6，-4π/9，π/4，0，0）。计算机配置为Intel（R）Core（TM）i5-10400F CPU @2.9 GHz，RAM 为8 GB。

将G-RRT*算法与加入固定概率目标偏置策略的RRT-Connect 算法和RRT 算法进行对比。RRTConnect 是一种双树搜索算法，从起点和目标点开始生成2 棵树同时进行搜索，因此搜索效率更高。本文所提G-RRT*算法与RRT-Connect 算法都由RRT算法改进而来，两者进行对比，可从横向说明所提算法的优越性。由于未加入目标偏置策略的RRTConnect 算法和RRT 算法盲目性太大，且机器人关节空间是六维的高维空间，使得2 种算法在有限时间内无法搜索到一条可行路径，所以本文在RRTConnect 算法和RRT 算法基础上加入固定概率目标偏置策略后再与G-RRT*算法进行对比。

设置3 种算法的目标偏置值均为0.5，选取100 次实验中路径长度最接近平均数的1 次实验结果，如图8-图10 所示，其中X，Y，Z为机器人所在空间的三维坐标轴。在图8（a）、图9（a）、图10（a）中，树枝形状的线段表示算法搜索过程，红色曲线为映射到笛卡尔空间中的机器人末端路径。由于RRT 算法本身的随机性，搜索出的路径并不平滑，难以被机器人直接执行，所以本文采用基于五次多项式的最小二乘法对关节角度进行后处理，使路径更加光滑，这也是最终路径没有经过所有路径点的原因。由于第1 关节在笛卡尔空间中的位置是不变的，所以图8（b）、图9（b）、图10（b）中只展示了关节2-关节6 的末端路径，可以看出，各关节均不与障碍物交涉。由图8（c）、图9（c）、图10（c）可看出，机器人按照规划路径运动可以完美避开障碍物，到达目标点。

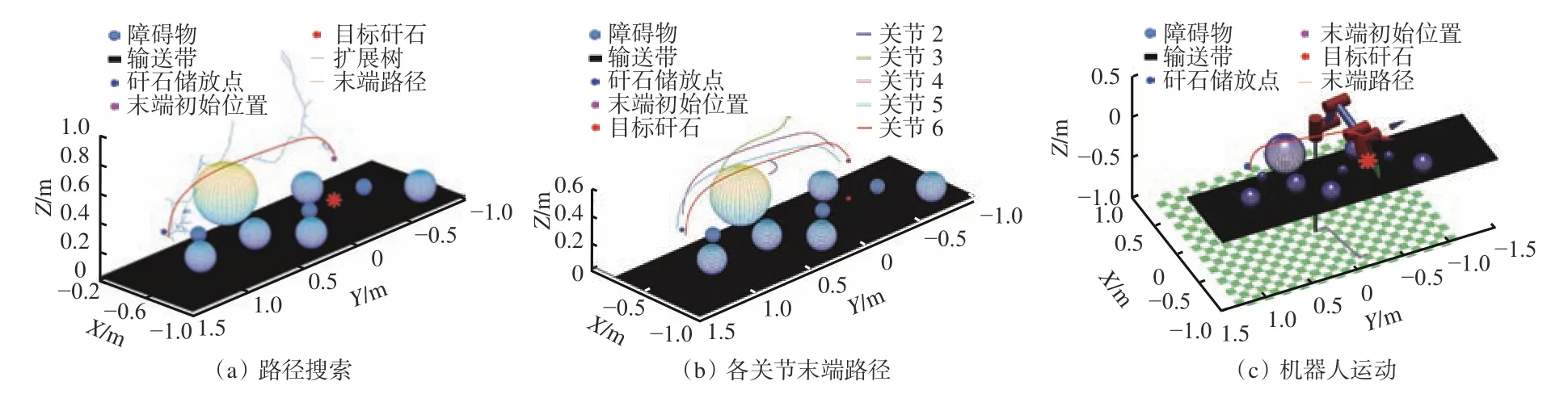
图8 引入固定概率目标偏置的RRT 算法实验结果Fig.8 Experimental results of RRT algorithm introducing fixed probability target bias

图9 引入固定概率目标偏置的RRT-Connect 算法实验结果Fig.9 Experimental results of RRT-Connect algorithm introducing fixed probability target bias

图10 G-RRT*算法实验结果Fig.10 Experimental results of G-RRT* algorithm

使用3 种算法进行100 次实验的结果对比如图11所示，算法性能参数对比见表1。在关节空间中，用关节角弧度衡量路径长度。从实验结果可看出，RRT-Connect 算法搜索效率比其他2 种算法高，但得到的路径最长。本文的目的是尽可能求得最短路径，采用G-RRT*算法得到的路径长度平均值小于其他2 种算法，因而更适用于煤矸石分拣机器人路径规划。

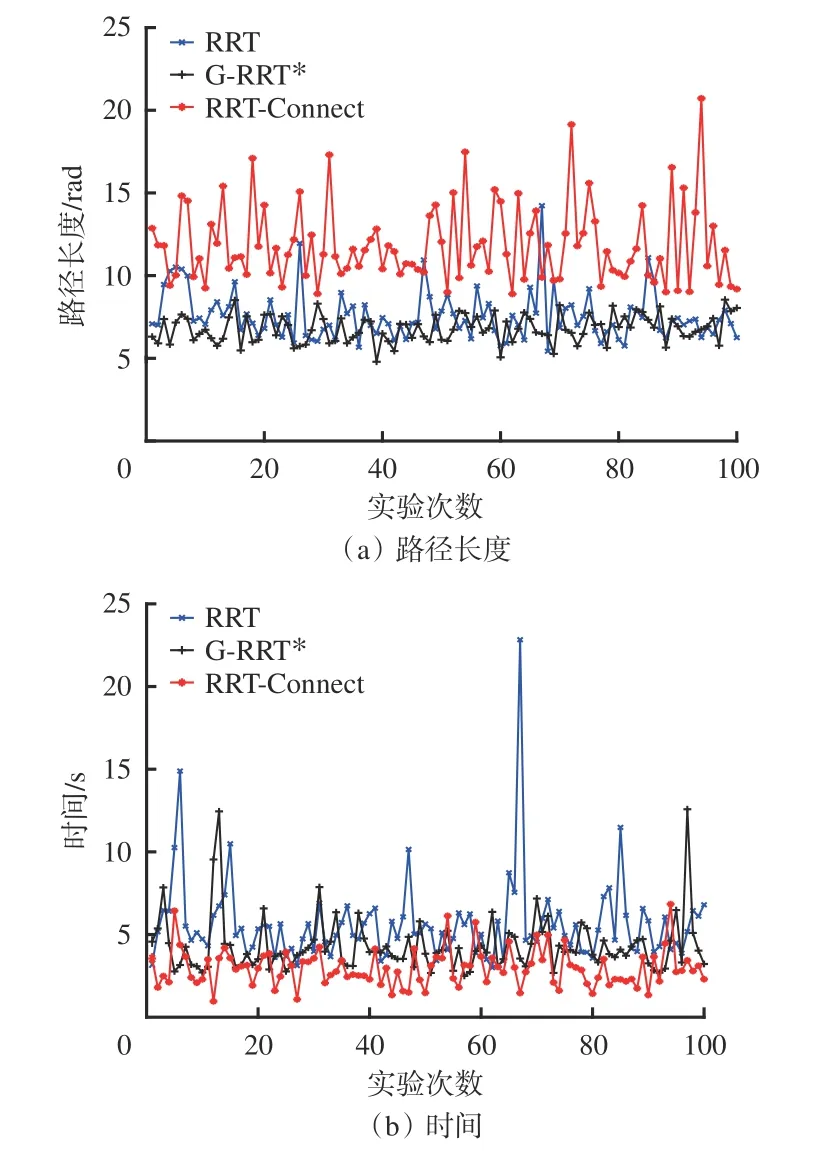
图11 3 种算法实验结果对比Fig.11 Comparison of experimental results of three algorithms

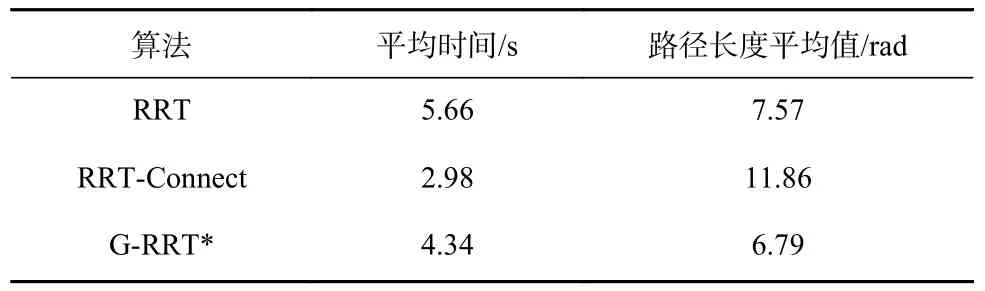
表1 算法性能参数对比Table 1 Comparison of algorithm performance parameters

5 结论

（1）分析了煤矸石分拣系统原理，设计了煤矸石分拣机器人路径规划方案。该方案融合了笛卡尔空间和关节空间的优点，不需要对机器人进行运动学求逆，且可避免在关节空间中描述障碍物。

（2）针对RRT*路径规划算法存在盲目性的问题，提出一种变概率的目标偏置策略。该策略在无障碍物区域增大目标偏置概率值，以增强算法的目标导向性，而在障碍物区域减小目标偏置概率值，以保证算法的避障能力。将变概率的目标偏置策略与RRT*算法相结合，提出G-RRT*算法，既保留了RRT*算法路径长度渐进最优的特点，也提高了算法的目标导向性。

（3）实验结果表明，与加入固定概率目标偏置策略的RRT-Connect 算法和RRT 算法相比，采用GRRT*算法得到的路径长度平均值最小，更适用于煤矸石分拣机器人路径规划。

（4）考虑到路径规划过程中步长变化会影响算法效率，在未来的研究工作中将针对步长随概率变化情况进行相关实验，以期进一步提高算法效率。同时，考虑将G-RRT*算法应用于煤矿现场真实场景中，以检测该算法存在的问题，便于提出改进策略。