基于EMD-TAR组合模型的滑坡位移预测研究

陈 曦，高雅萍，涂 锐

(1.成都理工大学地球科学学院，四川 成都 610059；2.中国科学院国家授时中心，陕西 西安 710600)

滑坡监测得到的地表位移数据经过科学处理和有效预测，可以得到滑坡体未来一段时间内的位移趋势变化，这对滑坡灾害防灾减灾方案的制订有重要的数据决策支持作用，对于滑坡灾害的预报预警具有非常重要的意义。

目前，运用较多的预测模型有统计机器学习模型、灰色模型、回归模型、时间序列模型等[1,4]，其中神经网络模型、灰色模型、自回归模型等在滑坡位移预测中应用较多[2]；数据序列的分解方法有小波分解、EMD、EEMD、VMD等[1,3,5-6]；许多学者将数据分解方法和预测模型进行组合预测，预测精度相对提高。宋丽伟[5]对位移序列进行经验模态分解和模态重构，利用LSTM模型组合预测，为“阶梯状”滑坡位移的预测提供了一种可行的思路。鄢涛等[6]利用极限学习机(ELM)对大坝变形的EEMD不同分解分量引入影响因子分别预测并叠加，预测精度有所提高。但这些预测模型都需要较多的累积观测数据进行样本学习，在实际监测过程中当影响因子监测数据积累不足或者影响因子数据误差较大与位移相关性较少时，位移预测就会比较困难，预测精度较低，需要应用对单位移序列拟合预测效果较好的模型，使滑坡位移预测结果有较高的精度。吴栋等[7]对比研究了LSTM 和SVM对VMD分量位移的组合预测发现LSTM更能有效地预测滑坡位移变化的本质规律。简文彬等[8]、杨大明[9]利用门限自回归模型进行了地基沉降预测。针对这样的问题，选择了应用较广泛的经验模态分解(Empirical Mode Decomposition,EMD)分解方法和对非线性非稳态序列预测效果较好的门限自回归模型(Threshold Auto Regressive,TAR)[10-12]，以组合的形式预测滑坡位移变化。门限自回归模型[13]是在自回归 (AR) 模型的基础上增加了门限区间约束条件,是对一类非线性的时间序列进行局部线性逼近的非线性时间序列模型。

本文以三峡库区秭归县白水河滑坡为例，首先利用经验模态分解方法将GPS滑坡地表监测水平累计位移分解为不同频率位移分量，然后利用门限自回归模型对各位移分解序列进行独立预测，最后模态叠加得到最终预测位移序列。选取MAE、MRE、RMSE和拟合优度4种精度指标来准确评价组合模型的精度，通过与BP(Back Propagation)神经网络模型、长短时间记忆网络模型的单一或组合模型对比验证其准确性，为滑坡的位移预测提供一种新的方法。

1 主要方法

1.1 经验模态分解

经验模态分解(Empirical Mode Decomposition,简称EMD)以数据序列的时变特征为基础，可将序列中存在的各种具有一定周期性规律的不同变化频率的分量分离单独存在。

对于滑坡位移数值序列，由于各种因素的影响，实测数据会存在各种模式的波动变化，也就是由若干个不同频率的数值波形序列所混合构成的，是不同变化频率数值序列的复合非线性数据，EMD分解的目的就是为了分解出其中的位移本征模函数，将复杂位移序列分化为多个近似单一频率的位移序列形式。

EMD分解方法：在原位移序列极值点基础上用三次样条曲线拟合形成上下包络线，计算上下包络均值作为第一个位移序列分离分量，将原位移序列减去该分量，得到1个新的位移序列。新序列若还存在局部极值，说明还不是1个无波动趋势序列，需要继续进行拟合分解，使用上述方法得到第一个分量后，用原始序列减去该分量，作为新的数据序列，可以得到所有剩余分量，以此类推，直至完成经验模态分解得到趋势变化序列。

1.2 门限自回归模型

门限自回归(Threshold Auto Regressive,TAR)模型对于存在较规律波动变化的时间序列预测效果较好。由于门限的分割，该模型对数据序列可以分段处理，详细描述序列的变化情况。

自回归(Auto Regressive,TAR)模型是分析数据内部相关关系的方法，假设存在观测时序{xt}，则定义p阶自回归模型，简称AR(p)：

xt=φ0+φ1xt-1+…+φpxt-p+εt

(1)

式中，φp不为0，{φp}为自回归系数序列；εt为零均值白噪声序列。

φ0+φ1+…+φp<1对于平稳的自回归模型，其自相关系数满足如下递推关系：

ρk=φ1ρk-1+φ2ρk-2+…+φpρk-p

(2)

(3)

AR模型的参数估计采用最小二乘估计，估计自回归系数序列{φp}，建立各参数矩阵,Y为AR模型预测矩阵，X为AR模型样本矩阵，φ为AR模型自回归系数矩阵，ε为零均值白噪声序列：

(4)

线性方程组为：

Y=Xφ+ε

(5)

自回归系数最小二乘估计为：

φ=(XTX)-1XT(Y-ε)

(6)

误差方差的最小二乘估计为：

(7)

AR模型的定阶采用贝叶斯信息准则：

(8)

其中,N表示样本序列长度,σ2表示样本残差的方差，使得BIC达到最小值的p即为该准则下的最优 AR 模型的阶数。

TAR模型是分段的AR模型，通过在观测时序{xi}的取值范围内引入k-1个门限值ri(i=1,2,…,n-1)，将该整个时间序列分成n个门限区间，可用r0,rn分别表示上界和下界，并根据延迟步数d按{xi-d}值的大小分配到不同的门限区间内，再对区间内的xi采用不同阶数的自回归模型(AR模型)，从而形成时间序列的非线性分段动态详细描述，其模型形式见式(9)：

(9)

(10)

2 EMD-TAR组合预测模型

首先利用经验模态分解方法对GPS滑坡监测地表位移数据进行序列分解，得到不同变化频率的位移序列，对各变形分量独立采用门限自回归模型进行预测，避免各分量误差相互影响，最后将所有形变分量模态叠加得到最终滑坡地表位移数值预测序列。其优势是利用门限自回归模型的对复杂非线性数据序列预测效果较好的特点，结合EMD分解算法的只用依据序列自身时间特征的特点，极大地提高了滑坡形变监测单位移序列的精度。该文组合预测模型数据处理步骤见图1。

图1 组合模型预测分析步骤

所采用的滑坡位移预测模型的精度评价指标包括平均绝对误差(Mean Absolute Error，MAE)、均方误差(Root Mean Square Error，RMSE)、平均相对误差(Mean Relative Error，MRE)、拟合优度R2,计算式为:

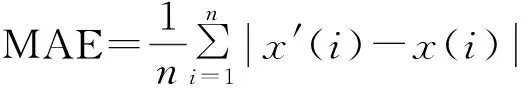
(11)

(12)

(13)

(14)

3 工程应用及模型验证

以三峡库区秭归县白水河滑坡GPS地表位移监测数据为例，滑坡体呈阶梯状向长江展布，为堆积层滑坡，坡体属顺向坡。滑坡体共布设11个GPS监测点，选择滑坡体中下部监测点ZG118和滑坡体北东部监测点DX-02对滑坡体不同位置形变位移进行预测描述，数据来源于国家冰川冻土沙漠科学数据中心 (http://www.ncdc.ac.cn)。

ZG118监测点为从2006年12月至2012年12月，共73期GPS地表位移观测数据。为提高单序列位移的预测精度，首先利用EMD对GPS监测点水平位移序列进行模态分解，迭代次数设置为200次，得到5个不同变化频率的IMF分量和一个残差分量，残差分量作为粗差剔除。各IMF分量见图2。

a)IMF1

将73期滑坡位移数据中的1—50期作为训练样本，51—73期数据作为预测检验值。建立门限自回归预测模型，门限区间个数取2，最大门限延迟量设置为5，自回归最大阶数为5，默认最小AIC值为1E+10,便于后续优化AIC值获得最优多维参数。按样本的30%～70%分位区间以1%进度搜索最优门限值。每组分量预测步长为一步，预测后数据更新，再进行下一步预测，实现模型的动态更新和预测。

为验证所建立组合预测模型的精度，分别建立EMD-TAR模型、EMD-LSTM模型、EMD-BPNN模型、TAR模型、LSTM模型对该滑坡位移序列进行预测，组合模型EMD-TAR模型、EMD-LSTM模型、EMD-BPNN模型[14-15]的预测方法为分别利用TAR模型、LSTM模型、BPNN模型预测每个IMF分量，最后时序合成得到实际滑坡预测位移序列，各模型的预测结果见图3。

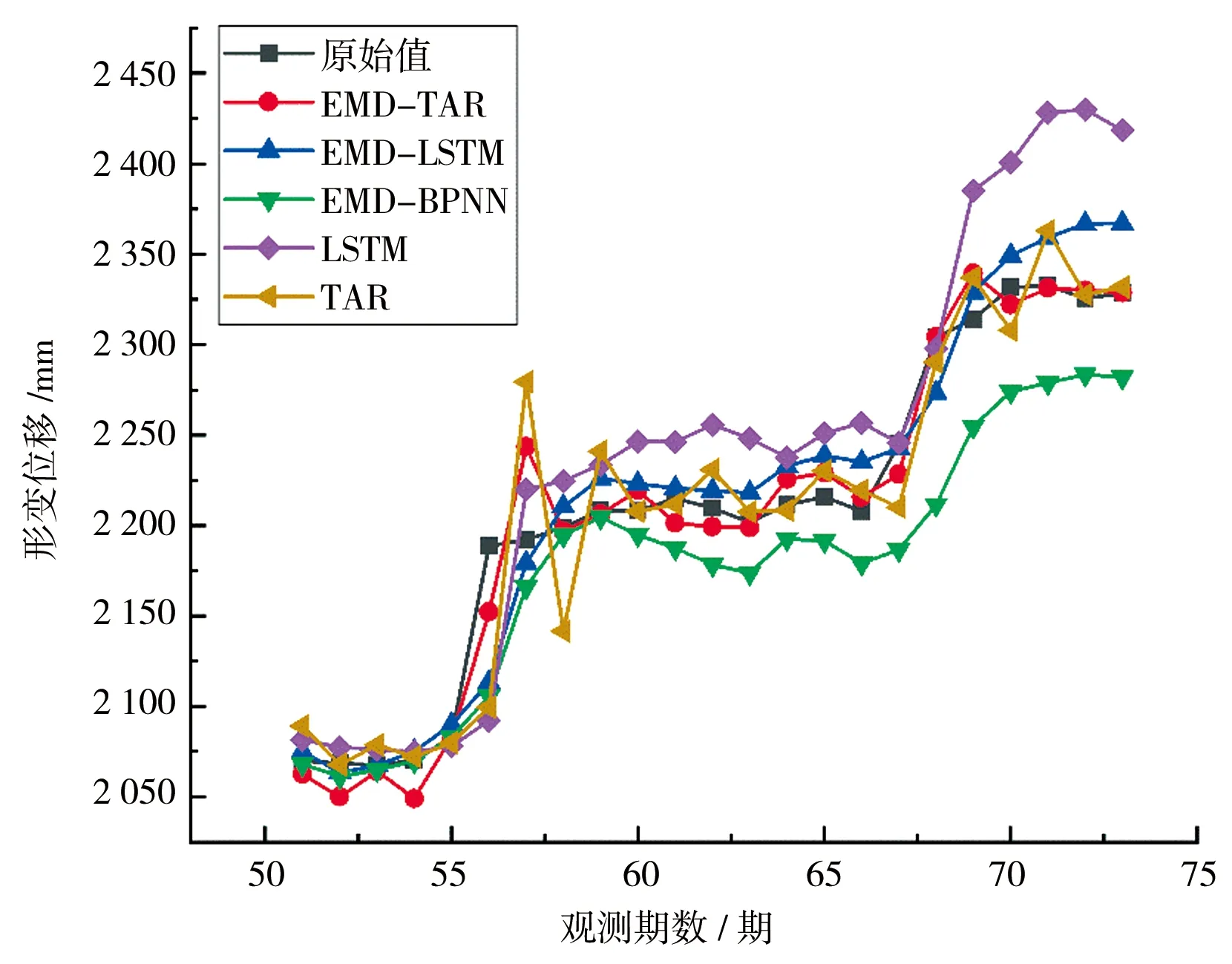
图3 各模型预测结果曲线序列

由图3可看出，单一TAR模型的预测效果比LSTM和BPNN更好，LSTM和BPNN单一模型会随着时间推移预测误差变大。相对于单一TAR模型和其他组合模型，组合EMD-TAR模型与原始位移序列拟合度较高，拟合优度最高，较为符合原始位移的变化趋势。为了准确评价模型的整体预测精度，对比计算几种预测模型的精度评价指标，结果表明，所建立的EMD-TAR预测模型在MAE、RMSE、MRE和拟合优度上均大幅提高。各模型精度评价值见表1。

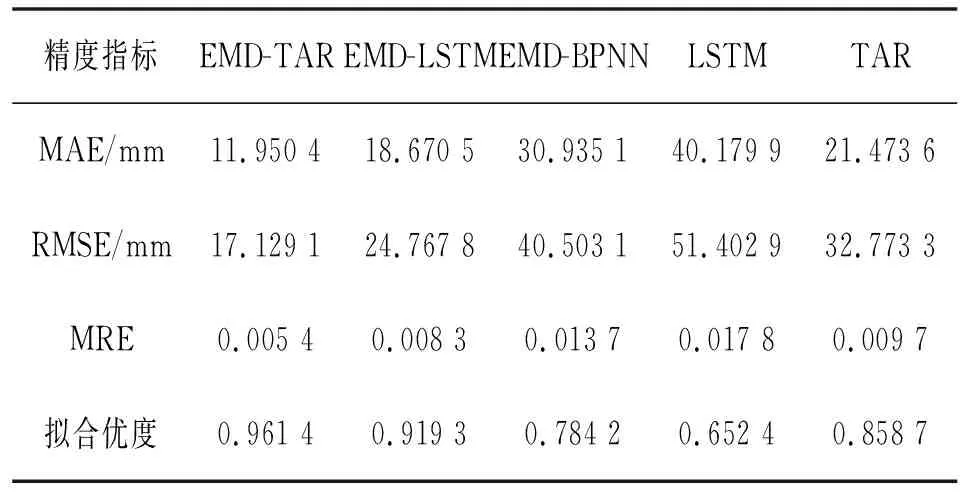
表1 各模型精度评价

为更好地验证所建立预测模型的精度和可靠性，选取滑坡体另一监测点进行预测实验，DX-02监测点为从2006年12月至2010年8月，共45期GPS地表位移观测数据，1—32期作为训练样本，33—45期数据作为预测检验值。EMD模态分解迭代次数设置为2 000次，得到5个不同变化频率的IMF分量和一个残差分量，残差分量作为粗差剔除。各IMF分量见图4。所建立门限自回归预测模型中门限区间个数设置为2，最大门限延迟量设置为5，自回归最大阶数为5，默认最小AIC值为1E+10。考虑到分量频率的变化因素，其中IMF1按样本的30%～70%分位区间以1%进度搜索最优门限值，IMF2-4按样本的30%～50%分位区间以1%进度搜索最优门限值。每组分量预测步长为一步，预测后数据更新，再进行下一步预测，实现模型的动态更新和预测。

a)IMF1

同样，以此监测数据为例，分别建立EMD-TAR模型、EMD-LSTM模型、EMD-BPNN模型、TAR模型、LSTM模型对该滑坡位移序列进行预测，组合模型EMD-TAR模型、EMD-LSTM模型、EMD-BPNN模型的预测方法为分别利用TAR模型、LSTM模型、BPNN模型预测每个IMF分量，最后时序合成得到实际滑坡预测位移序列，各模型的预测结果见图5。

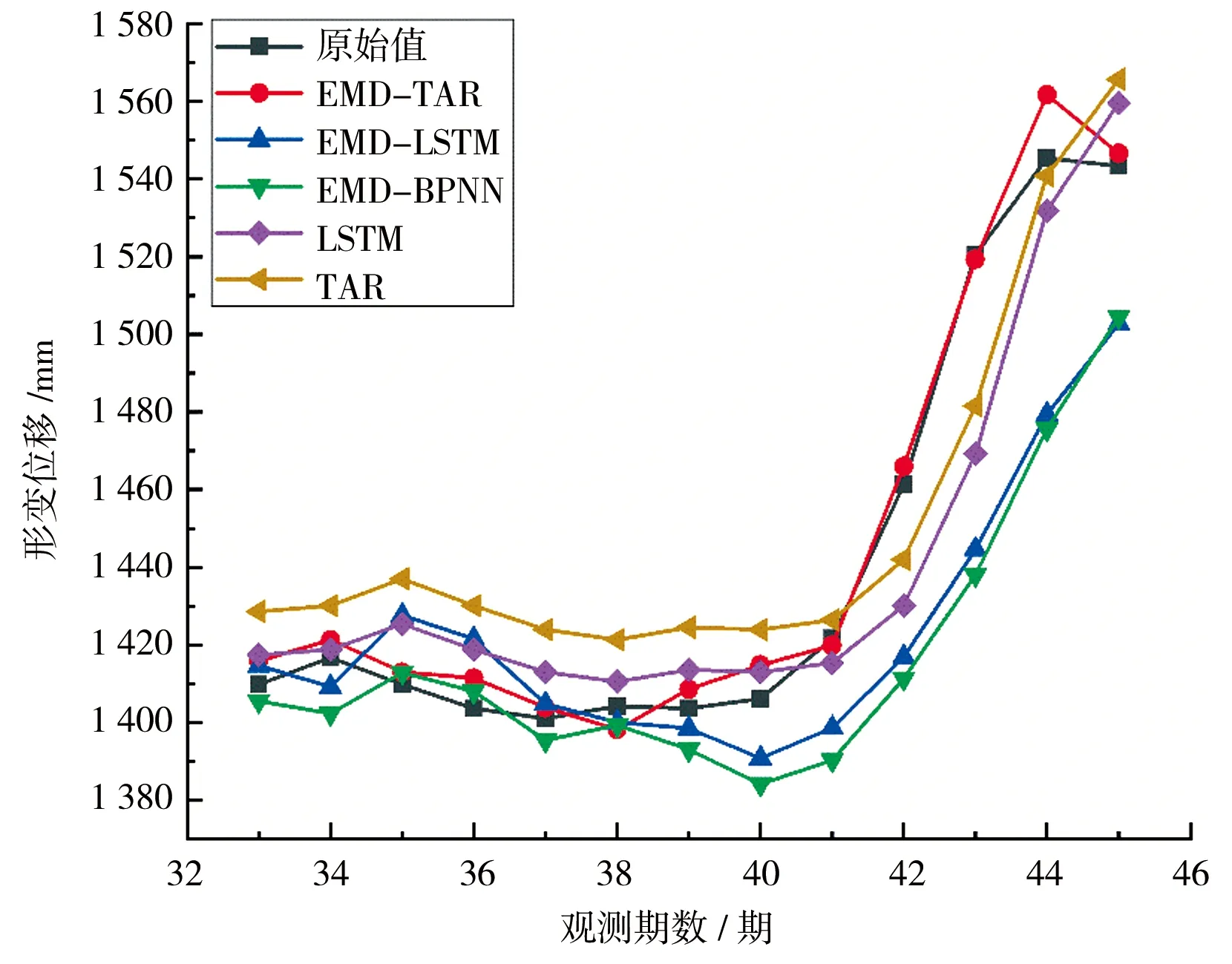
图5 各模型预测结果曲线序列

由图5可看出，组合EMD-TAR模型与原始位移序列拟合程度最高，最符合原始位移的变化趋势。参考分析2个算例的各模型预测结果曲线图，样本数据量和预测时间的变化对组合EMD-TAR模型影响较小，模型预测较稳定。在算例一中EMD-TAR、EMD-LSTM模型预测结果误差较小而在算例二中EMD-TAR、LSTM模型预测结果误差较小，样本数据量变化对LSTM及其组合模型的预测精度产生了影响，算例二较算例一数据量减少，EMD分解后的不同频率分量变少，算例二滑坡位移的整体变化趋势较算例一小，所以在算例二中，对未分解的滑坡位移进行预测的LSTM模型的预测效果相比EMD-LSTM模型更好，综合分析得到EMD-TAR在预测精度和稳定性上更优。

为了准确评价模型的整体预测精度，计算几种预测模型的精度评价指标，结果表明，该文所建立的EMD-TAR预测模型在MAE、RMSE、MRE和拟合优度上均大幅提高。各模型精度评价值见表2。

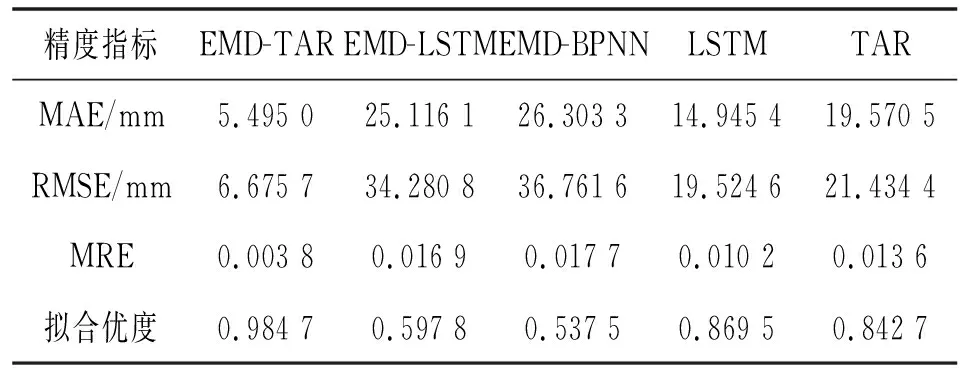
表2 各模型精度评价

4 结论

基于EMD算法和TAR模型构建了EMD-TAR滑坡位移预测模型，针对的是在实际监测过程中当影响因子监测数据积累不足或者影响因子数据误差较大与位移相关性较少的情况,利用EMD算法将非稳态的GPS监测滑坡位移序列分解为在时间尺度上具有不同变化频率的多个分量，对AR模型进行门限改进得到TAR模型，结合TAR模型对非线性波动数据序列预测效果较好的优势，对滑坡位移序列进行分解、预测、再叠加得到精度较高的预测结果。经过白水河滑坡实例数据的试验验证，该组合模型相比于单一TAR模型、LSTM和BPNN模型及其组合模型预测精度更高，为滑坡位移的预测提供了一种新方法。但该模型在滑坡环境影响下监测数据积累不足或影响因子关联较小时对位移的预测具有一定的局限性，后续可与其他顾及影响因子的模型进行组合预测研究。