大兴安岭地区的冻土热状态模拟1)

黄帅 丁琳 丁黔 胡争 王鹤 陈克政

(黑龙江大学，哈尔滨，150000) (黑龙江省生态地质调查研究院) (东北林业大学)

中国多年冻土主要分布在东北大小兴安岭及西部青藏高原地区。据统计，现存中国多年冻土总面积为1.59×106km2，其中东北高纬多年冻土面积为0.24×106km2(约占15%)[1]。受气候变化、人类活动的影响，东北多年冻土正在发生快速的变化[2-4]。而随着基础设施建设的发展，诸如高铁、管道、隧道等工程项目在中国东北地区逐步开展，建立在冻土区上的寒区工程也备受快速变化的冻土所影响，因此开展区域冻土热状态的模拟，对寒区工程建设、生态环境变化评估具有重要意义[5-7]。

对中国东北部永久冻土的研究，主要依赖于地质调查、公路和铁路以及中俄输油管道等工程走廊沿线的研究[8-13]，不能完全反映中国东北部多年冻土的空间变化和异质性。随着冻土学科与遥感、GIS等技术快速发展，冻土模型、冻土热状态模拟方法发展迅速，计算方法总体上分为经验模型、平衡模型、数值模型(物理模型)[14-16]。

在东北大兴安岭地区，由于其地理特性，目前开展该区域的冻土分布模拟研究较少。由于该区域地形地貌复杂，难以开展大范围的地质调查，因此该区域对于冻土的水热、物理参数累计较少。冻结数模型与等效纬度模型，曾被应用与模拟东北地区的冻土分布[7，17]，研究主要依据气象站提供的地表、大气温度数据对该区域的冻土参数进行统计回归，得到经验模型，但模型精度很大程度上受到了气象站个数的影响。本研究在大兴安岭地区内沿北向南选取4个试验点(二十四站、塔尔根、临海、古源)，应用库德里亚夫采夫(Kudryavtsev)模型(平衡模型)、一维瞬态传热的数值模型(物理模型)对研究区多年冻土活动层厚度与热状态进行模拟；对比实测地温与模型模拟地温，检验模型模拟精度；依据模拟精度、计算成本，比较2种模型的实际应用价值。旨在为未来区域冻土分布模拟提供参考。

1 研究区概况

大兴安岭位于黑龙江省北部地区，该地区具有高纬度、低海拔、低温时间漫长、植被覆盖率高、积雪覆盖持久等地理特征[18]，广泛分布着兴安-贝加尔型多年冻土(生态敏感型冻土)，冻土的分布特征具有显著的纬度地带性(见图1)，局地因子也一定程度地影响着该地区多年冻土的发育。受气候变化的影响，近50 a来大兴安岭地区多年冻土正在发生着快速变化[19-20]。

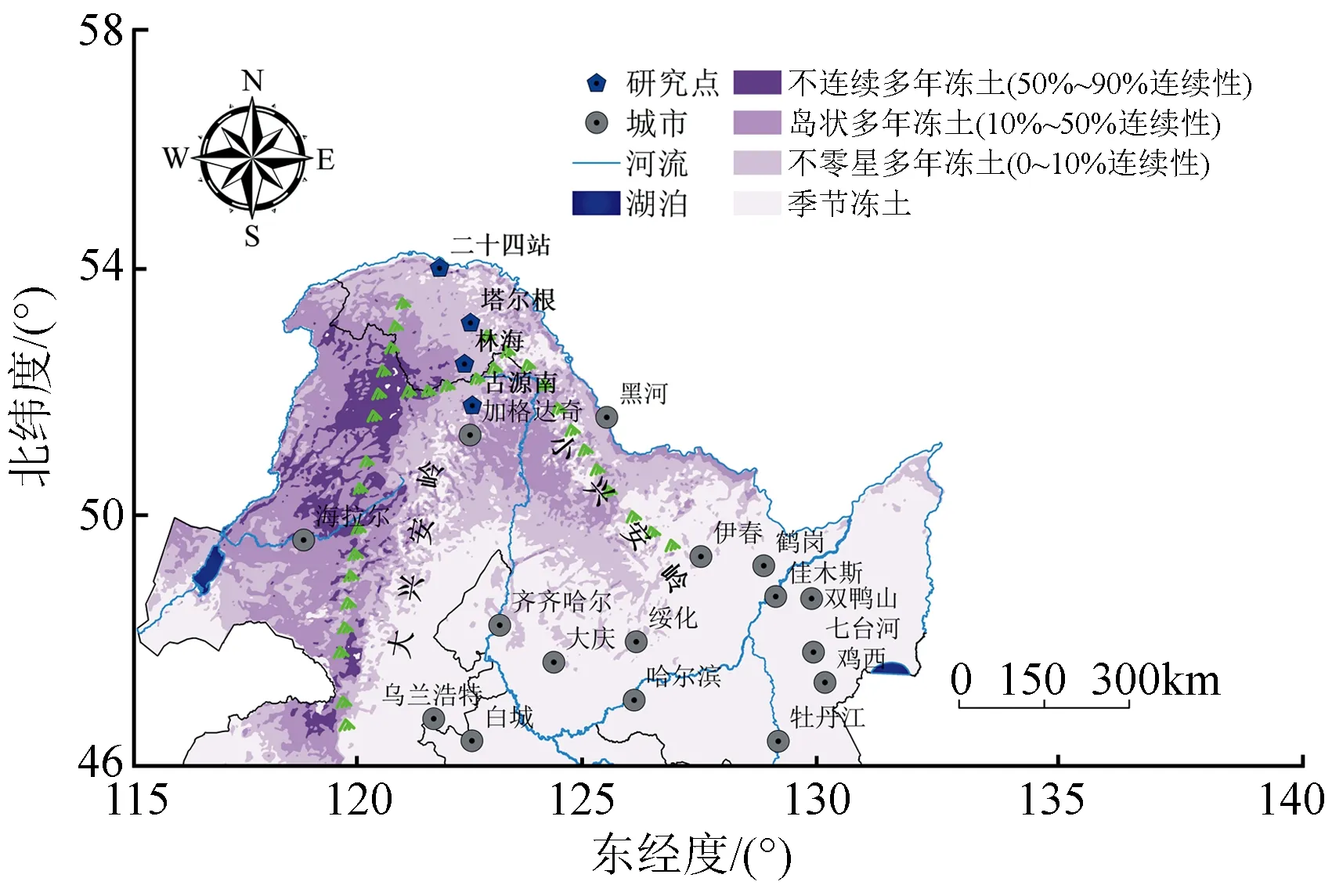
图1 研究区冻土分布

受冻土退化的影响，大兴安岭地区冻土灾害频发，诸如滑坡、崩塌、热融湖塘扩展、热融喀斯特等[21-22]。在退化过程中，土壤中有机碳逐渐分解并释放，地表水热平衡遭到破坏，影响了地表植被演替，也加速了气候变暖的进程[2]。

本研究在大兴安岭地区内设置4个试验点，沿北向南分别为二十四站、塔尔根、临海、古源(见表1)，从纬度地带性看，从北向南年均气温逐渐降低，但年均地温却受到了局地因子影响，如二十四站年均地温高于南部站点的地温。

表1 试验点年均气温与年均地温(2015—2017年)

试验点附近，仅有新林气象站(122°31′E，52°58′N)与试验点相邻。该气象站记录的2014—2015年的气温与地表温度(见图2)，2014年年均气温为-2.3 ℃、年均地表温度为4.9 ℃。由图2可见：冬季地表温度显著高于气温，说明植被与积雪具有较好的保温效果，局地因子影响效果显著。

图2 新林气象站记录的2014—2015年气温与地表温度

2 研究方法

2.1 一维传热数值模型

一维传热模型是依据热扩散偏微分方程建立的物理模型[16]，模型构建见式(1)～(3)。

ρ·C(∂T/∂t)=(∂/∂x)[λ(∂T/∂x)]+

(∂/∂y)[λ(∂T/∂y)]；

(1)

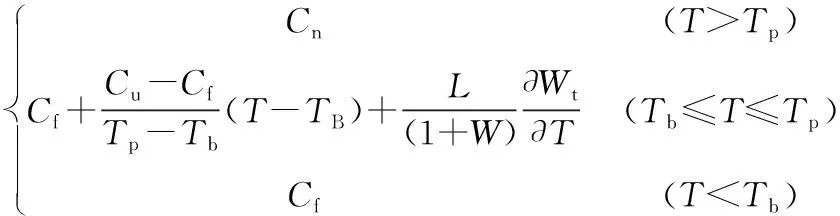
(2)

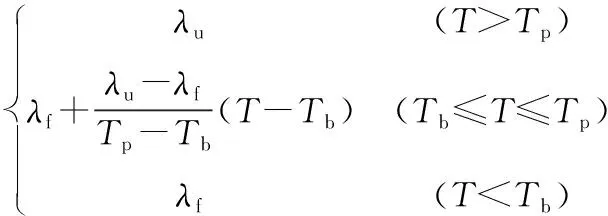
(3)

式中：C为考虑冻土相变的等效比热(单位为J·kg-1·℃-1)；ρ为土的天然密度(单位为kg·m-3)；λ为土的导热系数(单位为W·m-1·℃-1)；Cu、Cf分别为融土及冻土的比热容(单位为J·kg-1·℃-1)；L为水的相变潜热(单位为J·kg-1)；λu、λf分别为融土及冻土的导热系数(单位为W·m-1·℃-1)；W、Wt分别为冻土的总含水量及含冰量(用百分比表示)；Tp、Tb分别为冻土剧烈相变区的上、下界温度(单位为℃)；T为温度变量(单位为℃)；t为时间变量(单位为s)；x为沿某方向的空间变量(单位为m)。

未冻水含水量根据式(4)确定：

Wt=a|T|-b。

(4)

式中：a、b为量纲为1的常数，根据不同土质类型由拟合经验公式确定。

模型边界条件以地表上2 m处气温作为输入，见式(5)：

T(t)=Ta+A0sin[(2π/8 760)t+π/2]。

(5)

式中：Ta为年平均地表温度(单位为℃)；A0为气温年较差(单位为℃)。

2.2 库德里亚夫采夫模型

库德里亚夫采夫(Kudryavtsev)模型是一种常用的平衡方程模型，用于计算冻土的活动层厚度与多年冻土顶板温度[16]。计算方法见式(6)～式(8)。

(6)

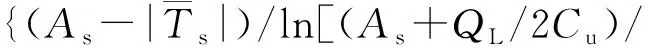
(Ts+QL/2Cu)]}-QL/2Cu；

(7)

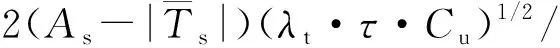
(2AZCu+QL)。

(8)

式中：Z为最大季节冻结深度或最大季节融化深度(单位为m)；Ts为年均地表温度(单位为℃)；As为地表温度年振幅(单位为℃)；τ为周期(8 640 h)；QL为土体中水的相变潜热(单位为J·m-3)；Az为季节冻结(融化)层内温度的平均较差(单位为℃)；ZC单位为m，无实际物理意义。

2.3 模型输入参数

2.3.1 土层参数

根据现场钻孔取样，得到的地层土的工程分类见图3。

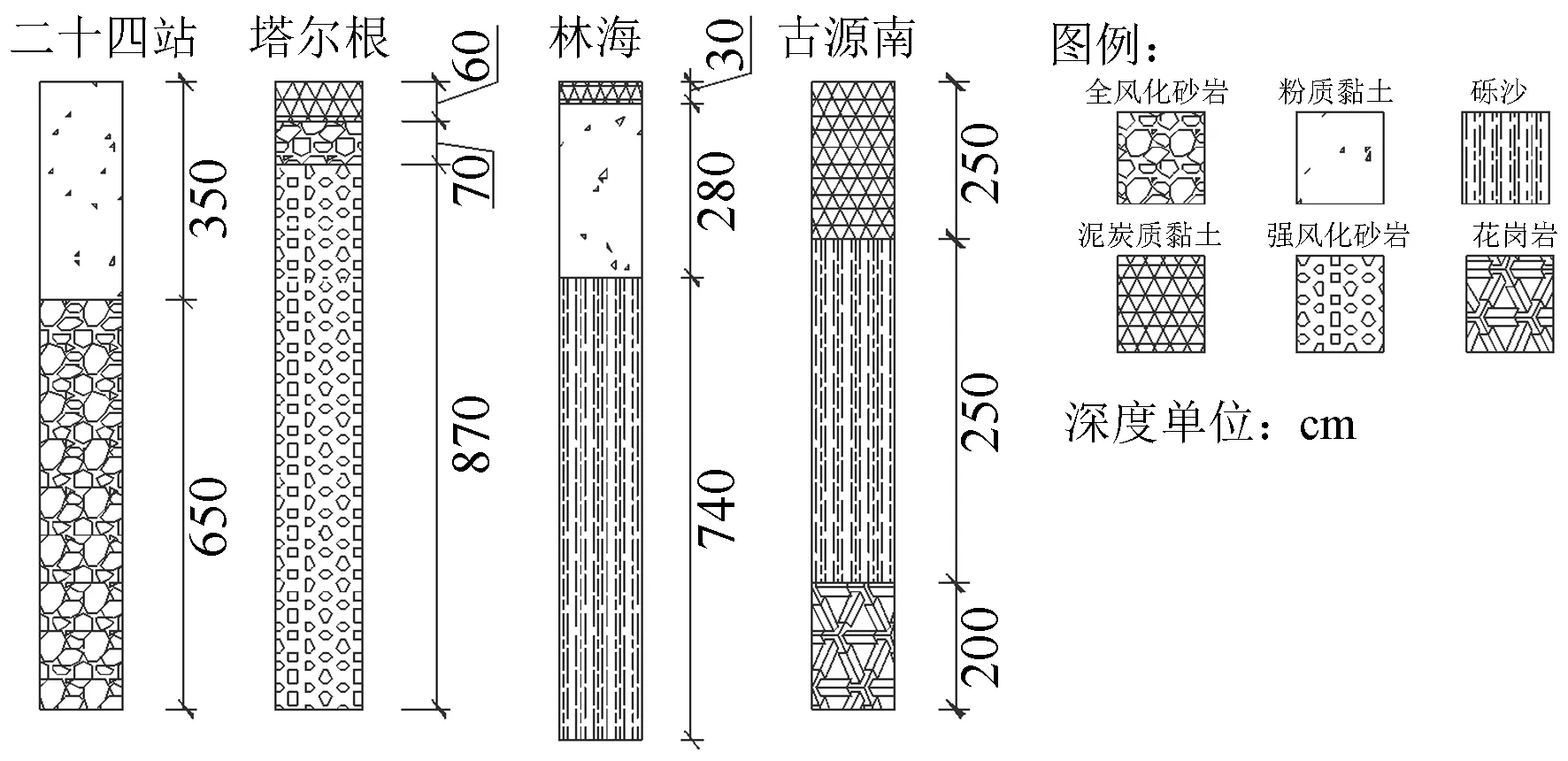
图3 试验点地层信息

土体热参数根据试验数据与文献进行赋值[23]，未冻水参数(a、b)根据文献给出的参数进行赋值[24]，土体参数见表2。

表2 研究区土体的物理参数

2.3.2 一维传热模型的边界条件

试验点地表温度由现场埋设传感器监测所得(见图4，2015年)；气温数据采用美国国家航空航天局(NASA)提供的气温再分析数据产品，时间分辨率为8 d、空间分辨率为1 km(见图5)；应用三角函数拟合获得年均气温与气温振幅。

图4 试验点地表温度

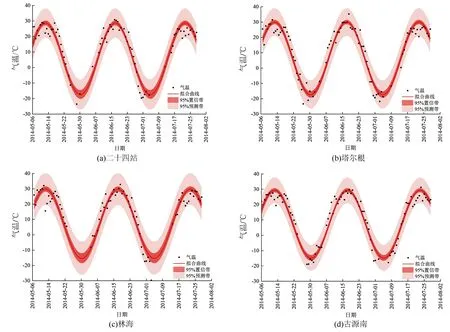
图5 试验点气温

3 结果与分析

3.1 模型计算值与钻孔监测值对比

根据试验点的钻孔实测地温(见图6)，通过0 ℃等温线法获得试验点的活动层厚度与季节冻结深度，并计算年均地温(见表3)。

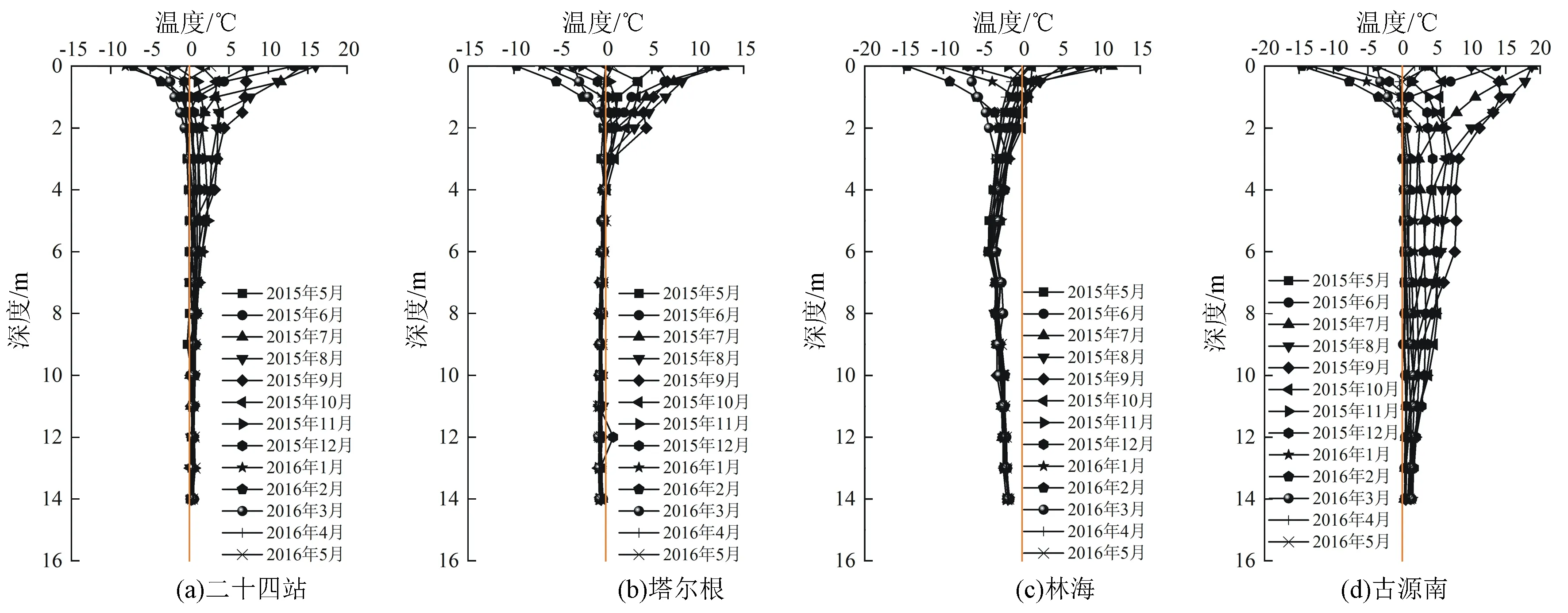
图6 试验点监测地温

表3 试验点活动层厚度与年均地温

利用一维热传导模型计算试验点冻土地温，对比实测与模拟值的最大季节冻结深度月份与最大季节融化深度月份的地温(见图7)，发现一维热传导数值模型对试验点的地温模型效果较好，预测值与实测值趋势基本一致。

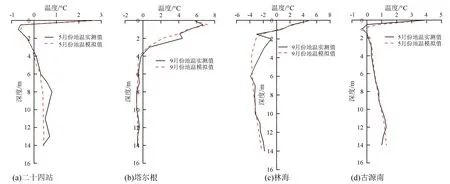
图7 试验点冻土地温的热传导模型模拟值与实测值

根据一维传热模型模拟的地温曲线，可绘制地温等值线图(见图8)；根据0 ℃最低位置可得到最大季节冻深与最大季节融深，对比库德里亚夫采夫模型与一维传热模型活动层计算值(见表4)。

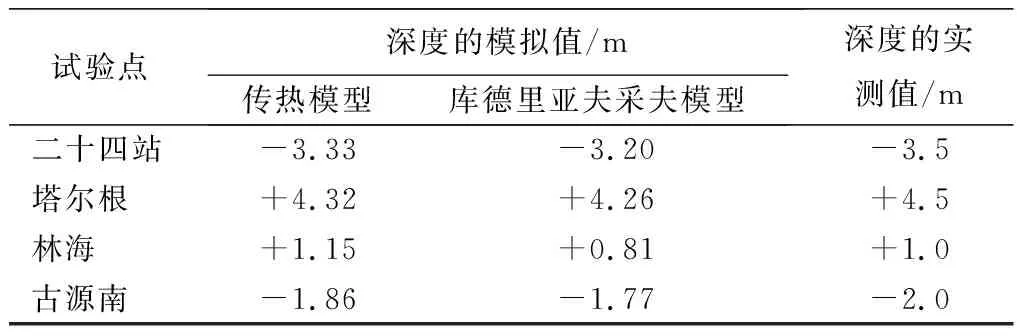
表4 试验点最大季节冻深和最大季节融深的模拟值与实测值

图8 塔尔根地温等值线

3.2 模型误差分析

对比库德里亚夫采夫模型、一维传热模型对试验点的活动层厚度与最大季节冻结深度模拟结果，一维传热模型的计算误差在0.14～0.18 m、库德里亚夫采夫模型的计算误差在0.19～0.30 m，一维传热模型的模拟精度优于库德里亚夫采夫模型。

模型的计算误差来源于多个方面。对于一维传热模型，一方面模型本身只考虑了传热问题，而活动层是水热迁移最为敏感的一层土层，由于水热迁移作用会影响热土体中的热传导与热对流，从而对模拟结果造成误差；另一方面，在地气热对流过程中，冬季的植被与积雪具有保温层的作用，使地表温度高于气温，夏季的植被与积雪阻碍了地表向大气的热传递，因此对于试验点中地表为裸地的古源南试验点，其模拟误差最小。

对于库德里亚夫采夫模型，一方面，在模型计算时，需假设地层为匀质土，而实际场地的地层往往较为复杂，这会造成一定的误差；另一方面，模型缺乏对局地因子影响参数，大兴安岭地区多年冻土受生态环境影响显著，诸如坡向、坡度、积雪、植被、海拔等因素均会对冻土赋存状态造成影响，若不考虑局地因子效应，则会造成一定的模型计算误差。

4 讨论与结论

对比一维传热模型、库德里亚夫采夫模型，在计算成本方面，库德里亚夫采夫模型显著优于一维传热模型，这是由于模型本身构成决定的；传热模型是依据偏微分方程构建的，而库德里亚夫采夫模型则是依据平衡等式建立的，其求解效率高于偏微分方程，但在计算精度方面，物理模型显著高于平衡方程模型。另一方面，物理模型能够对冻土的地温的动态发展过程进行全程模拟，能够反映出更多的冻土热状态参数，诸如年均地温、冻土顶板温度、多年冻土层厚度等。

在模型深入研究过程中，一方面可以考虑将水分场加入传热模型，构建冻土的水热耦合模型；另一方面，需要增加对于地表水热参数(如：地表温度、土壤含水量等)的时空变化反演的问题研究。

本研究应用一维传热模型、库德里亚夫采夫模型计算了大兴安岭地区4个试验点的冻土活动层厚度、最大季节冻结深度与地温，结果表明：一维传热模型对4个试验点的冻土地温模拟值与实测值具有一致的趋势，模拟结果较好，对于活动层厚度与最大季节冻结深度的模拟，具有良好的精度，误差范围在0.14～0.18 m之间，能够较好地满足工程计算的需求。库德里亚夫采夫模型在计算活动层厚度与季节冻结深度时，模型计算误差在0.19～0.30 m，基本能够满足工程计算需求。在计算成本方面，库德里亚夫采夫模型优于一维传热模型，该模型能够较好地应用于工程计算，提高工程效率。