砂土中浅埋圆或螺旋形锚板上拔承载机理数值分析

郝冬雪，袁 驰,2，陈 榕，张 新，史旦达，孔纲强

(1.东北电力大学 建筑工程学院，吉林 吉林 132012；2.北京工业大学 建筑工程学院，北京 100124；3.中国电力工程顾问集团东北电力设计研究院有限公司，吉林 长春 130021；4.上海海事大学 海洋科学与工程学院，上海 201306；5.河海大学 岩土力学与堤坝工程教育部重点实验室，江苏 南京 210098)

螺旋锚基础具有结构简单、施工方便、环境影响小等优点，在建筑、输电线路、海洋等工程中得到广泛的应用，其抗拔性能与平板锚相似，抗拔承载力预测是设计的关键。Ghaly和Hao等缩比尺模型试验和Hao等离心机试验结果表明，螺旋锚锚盘型式对承载力的影响很小，预埋螺旋锚与平板锚的上拔承载力基本相同。锚板上拔承载力计算主要有极限平衡法、极限分析法、有限元法、孔扩张分析法等，其中极限平衡法的应用最为广泛，该分析方法将滑裂面内土体视为刚体，无需考虑土体应力-变形关系，同时对滑裂面形式和滑裂面上的应力分布及大小进行了假设。

一些学者通过室内模型试验、离心机试验、现场试验及数值模拟的方法对锚板上拔破坏滑裂面提出不同的简化，包含圆柱面，倒锥台及曲面。对于沿滑裂面上的应力分布及大小，有研究者提出应力沿锚埋深呈线性分布，大小为侧压力系数

K

与自重应力的乘积，且

K

为常值，如Meyerhof等基于Adams等的试验结果，采用Caquot曲面滑裂面时的土压力系数

K

，经过形状修正系数

s

计算圆锚的侧压力系数为

sK

；Mitsch等所用

K

值与Meryerhof等相似，但考虑安装扰动的影响，

K

值减少了30%～40%；Murray等假设

K

=

K

=1-sin φ，φ为内摩擦角；Ghaly等采用被动土压力系数

K

；Giamapa等根据临界状态，提出侧压力系数

K

=cos(

φ

-ψ)，ψ为剪胀角；Hao等采用White等提出的条形锚板应力假设，即上拔过程中滑裂面上法向应力保持不变，确定了圆锚滑裂面法向应力系数

K

，如式（1）：

式中，φ为临界状态内摩擦角。

大多数极限平衡法包含的经验参数由缩比尺模型试验结果确定，在预测实际较大尺寸锚板上拔承载力时通常不准确，存在高估风险。因此，Cerfontaine等基于2维有限元软件PLAXIS，采用小应变硬化土本构模型(HS small)模拟大直径锚板上拔过程，探讨浅埋圆锚或螺旋锚抗拔机理及半解析解的可靠性。但对于具有应变软化的砂土，HS模型不能捕捉大应变时峰值后出现的软化现象，数值模拟会高估锚板的上拔承载力，尤其对于较大埋深比情况。为考虑砂土应变软化特性，陈榕等基于Abaqus平台采用改进的Mohr-Coulomb弹塑性本构模型，模拟密砂中圆锚上拔行为，揭示砂土渐进破坏过程，并分析尺寸效应产生的原因，但未对滑裂面上应力及上拔承载力计算理论等进行分析。

为更真实地模拟砂土压硬性、剪胀性及应变软化特性对锚板上拔破坏机理的影响，本文以Abaqus有限元软件为平台，基于陈榕等改进的Mohr-Coulomb本构模型及强度参数对应力的依赖关系，采用欧拉拉格朗日耦合法(CEL法)模拟不同密实度砂土中不同埋深比圆或螺旋形锚板上拔过程，探讨浅埋锚上拔破坏机理，分析破坏滑裂面形式及滑裂面上法向应力及土体强度参数的分布规律，提出了更准确地预测圆锚或螺旋锚上拔承载力的方法，同时对比分析已有的理论计算公式，并建议各公式的适用条件。

1 有限元模型及验证

1.1 有限元模型

为分析不同密实度砂土中圆锚或螺旋锚上拔承载机理，建立松、中密和极密砂中埋深比

H

:

D

=1.0～7.5的圆锚拉拔试验有限元模型。

1.1.1 计算模型

圆锚上拔承载问题为轴对称问题，故在Abaqus/explicit分析模块中建立四分之一锚-土耦合体系的三维模型。将土体设置为欧拉体，锚设置为拉格朗日体。为与离心机试验结果对比，锚盘直径

D

取为400 mm，螺距为0.25

D

，盘厚为0.05

D

，锚杆轴径为0.235

D

。考虑锚体刚度远大于土体，将锚设为刚体，忽略其变形，离散化为拉格朗日单元C3D8R，在锚顶部设置参考点，约束参考点的水平向位移和轴向转动。根据文献[22]，计算域从锚杆轴线径向取10

D

；锚盘底部向下取锚埋深

H

；为允许上拔过程中土体隆起和流入空的欧拉单元，地面以上竖向取5

D

，设置为零强度和刚度的空单元。计算域底部边界约束各方向位移；侧面边界约束速度和转角。计算域内土体网格规则划分，采用EC3D8R单元，锚板上下最大5

D

、水平向4

D

范围内网格密化，最小网格宽度Δ

B

在板边缘处，计算几何模型如图1所示。锚-土接触面采用自动识别，法向作用设为硬接触，切向作用采用罚函数法，摩擦系数设为0.3。在锚杆顶部参考点施加上拔位移1

D

，由于采用动态分析模块进行准静态分析，设置的加载时间应尽可能接近准静态；同时，为获得更稳定的结果，动力显示分析步中时间比例因子取0.6。

图1 数值计算模型Fig. 1 Numerical model

1.1.2 土体模型及参数

土体本构模型采用改进的Mohr-Coulomb弹塑性模型，模型参数包括变形模量

E

、泊松比

v

、初始侧压力系数

K

、等效塑性应变阀值ε及ε、峰值内摩擦角φ、峰值剪胀角ψ及临界状态内摩擦角φ。为与离心机试验结果进行对比，参考试验用土进行参数取值，其中，

v

=0.3，φ=31°，

K

=1-sinφ=0.485，ε=2%，ε=20%，对于相对密实度

D

=100%时，文献[21]根据锚埋深处的应力状态，给出该砂土

E

、φ、ψ等值。3种密实度砂土的密度分别为1.61、1.67和1.75 g/cm。中密及松砂的强度与变形参数φ和

E

按照

D

=60%和30%情况，参照Hsu等提出的公式进行线性插值计算；ψ根据Bolton提出的公式φ=0.5ψ+φ确定。各参数如表1所示。

表1 土性参数
Tab. 1 Soil parameters

Dr H:D φp/(°) ψp/(°) E/MPa 30%1.0 36.89 11.77 9.15 2.0 36.18 10.36 12.67 3.0 35.77 9.53 15.32 4.0 35.47 8.95 17.53 5.0 35.25 8.49 19.47 6.0 35.06 8.12 21.20 7.5 34.83 7.67 23.54 60%1.0 42.54 23.08 13.37 2.0 41.13 20.26 18.51 3.0 40.31 18.61 22.39 4.0 39.72 17.44 25.62 5.0 39.27 16.53 28.45 6.0 38.90 15.79 30.99 7.5 38.44 14.89 34.41 100%1.0 49.94 37.88 19.01 2.0 47.59 33.19 26.31 3.0 46.22 30.44 31.82 4.0 45.25 28.49 36.41 5.0 44.49 26.98 40.43 6.0 43.87 25.74 44.04 7.5 43.12 24.23 48.90

1.2 模型及计算结果验证

1.2.1 加载速率及网格密度的影响

考虑计算的稳定性及时效性，在批量计算之前，进行加载速率和网格密度影响的变参数计算。额外选择极密砂中更深埋（

H

:

D

=9）的情况进行对比计算，其中，土性参数φ=42.5°，ψ=23°，

E

=53.3 MPa。为分析加载速率的影响，取加载速率

V

=0.025

D

/s、0.050

D

/s、0.100

D

/s，以最小网格尺寸比Δ

B

:

D

=0.1进行计算，不同加载速率的位移-荷载半对数坐标曲线如图2（a）所示。由图2（a）可见，加载速率对上拔承载力的影响较小。当计算至0.5

D

上拔位移时，速率

V

和

V

计算时间约为

V

的12和2倍，从耗时和稳定性考虑选择

V

加载速率进行后续计算。为分析网格密度的影响，选择3种密度网格进行计算，最小网格尺寸比Δ

B

:

D

分别为0.05，0.10和0.20，对应划分的网格数量分别为613 130、280 864、125 856，不同网格密度的计算结果如图2（b）所示。由图2（b）可见，网格越疏，计算上拔承载力越大，Δ

B

:

D

=0.05和0.10两种情况的计算结果接近，但0.05网格密度比的计算时间为0.10网格密度比的6.6倍，因此，后续计算中采用最小网格尺寸比Δ

B

:

D

=0.10的网格划分方法。

图2 加载速率和网格密度影响Fig. 2 Effects of loading rate and mesh density

1.2.2 计算结果

图3为不同密实度砂土中不同埋深比锚板的上拔位移-荷载曲线，以半对数坐标形式绘制。埋深较浅时，位移-荷载曲线有明显峰值出现，峰值之后，承载力下降；随着埋深比增加，曲线特征发生变化，可分为初始直线段、弯曲段和后期平稳段（近似直线）3个阶段。锚板极限上拔承载力取曲线的峰值或曲线平稳段起点，图3中以空心圆表示，同时将极限上拔荷载时对应的破坏位移

u

、净极限上拔承载力

Q

（扣除锚自重）及上拔力系数

N

=

Q

/γ

AH

列于表2，其中，γ为土体重度，

A

为锚盘面积，

A

=π

D

/4。

表2 数值计算结果
Tab. 2 Numerical results for different conditions

Dr H:D up:D/% Qu/kN Nγ 30%1.0 0.878 2.135 2.70 2.0 1.778 7.581 4.78 3.0 2.098 17.544 7.37 4.0 3.488 34.367 10.83 5.0 7.375 55.762 14.06 6.0 9.120 78.409 16.48 7.5 13.896 121.184 20.37 60%1.0 1.756 2.596 3.12 2.0 2.234 9.360 5.70 3.0 3.010 21.516 8.74 4.0 4.412 41.638 12.68 5.0 7.205 71.510 17.42 6.0 8.208 106.075 21.53 7.5 12.312 158.159 25.68 100%1.0 1.550 3.409 3.95 2.0 2.579 12.727 7.38 3.0 3.308 29.239 11.31 4.0 4.904 55.998 16.24 5.0 6.886 94.478 21.92 6.0 7.786 139.106 26.89 7.5 12.625 221.950 38.06

图3 上拔位移-荷载曲线Fig. 3 Curves of uplift resistance and displacement

1.2.3 结果验证

为验证模型的准确性，将数值计算（FEM）结果与Hao等密砂中螺旋锚离心机试验结果进行比较，如图4所示。

图4 数值结果与离心机试验对比Fig. 4 Comparison between numerical and centrifugal tests results

由图4可见，随着埋深比增加，数值计算结果获得的

N

与离心机试验结果趋势相同；离心机试验的砂土密实度在85.8%～96.5%之间，其试验结果介于中密与极密砂的数值计算结果之间，验证了计算模型的可靠性。但从严格角度，数值模拟结果较离心机试验结果偏高，可能是由于按照Bolton关系式确定的剪胀角较实际情况偏大引起。

2 破坏模式

2.1 埋置深度及密实度对破坏模式的影响

图5为不同密实度土中不同埋深比锚板上拔破坏时对应的土体等效塑性应变云图，其中，应变超过2%区域以黑色显示，红线为郝冬雪及Giampa等建议的浅埋时理论破坏面，即与竖轴夹角为剪胀角的倒锥台面。

浅埋时，塑性区从锚盘边缘开始，向两侧发展，直至地表，形成贯通的剪切破坏带，而锚板上方有较大的弹性区，此弹性区会随锚埋深增加逐渐变小；除

H

:

D

=1外，上拔位移至一定值后，地表处杆周出现塑性区，并沿杆向下发展，锚埋深越大，杆周塑性区向下发展得越深，表明在一定范围内杆侧摩阻得到发挥，但由于杆轴径较小，侧摩阻力的影响很小。根据文献[26-27]，由最大剪应变值近似确定破坏面，则浅埋时，数值计算获得的滑裂面可视为直线，这种破坏模式为浅埋破坏模式；对于松砂和中密砂，数值滑裂破坏面与郝冬雪及Giampa等理论破坏面（红线）基本一致，而极密砂土中数值破坏面（绿虚线）与理论破坏面偏差稍大，

H

:

D

=2～6时，理论破坏面较数值破坏面外扩约5°。随着埋深增加，土体塑性区向锚盘外侧发展受限制，开始向锚盘正上方发展，其上方弹性区逐渐消失，数值破坏面与理论直线破坏面偏差增大，破坏面由斜面形式向朝杆轴弯曲的曲面发展，但依然会持续开展至地表，此破坏模式为过渡破坏模式，如松砂

H

:

D

=4～5，中密砂

H

:

D

=6和极密砂

H

:

D

=7.5。当埋深较大时，由锚盘边缘开始的塑性区不会连续发展至地表，而是局限在地表以下，呈梨状封闭面，出现了深埋破坏模式，如松砂

H

:

D

=6.0、7.5，塑性区开展高度为5

D

～6

D

。锚盘以上一定高度范围内应变等值线呈气泡状（深色区域），超过此高度，应变等值线近似呈直线向轴线收缩。

在不同密实度砂土中，随着锚埋深的增加，其破坏模式均会出现上述的浅、过渡及深破坏模式，但其出现过渡的埋深比会受土体密实度影响，土体越密实，过渡破坏模式出现的埋深越大。根据图5，松砂、中密砂和极密砂3种情况过渡破坏模式出现的埋深比分别为4.0、6.0和7.5。

图5 破坏时等效塑性应变云图Fig. 5 Contours of equivalent plastic strain at failures

2.2 浅埋滑裂面假设

数值计算结果表明，砂土中浅埋锚的破坏滑裂面基本为倒锥台型，倾角可近似为剪胀角。过渡埋深破坏面虽然在近地表时出现收缩，但按浅埋破坏模式开展至地表时，破坏面与地表的交点仍处于塑性范围，为简化后续计算，将过渡破坏模式按照浅埋破坏模式处理。因此，在理论计算时假设浅及过渡埋深时的滑裂面均为倾斜角度等于砂土剪胀角的倒锥台面。

3 滑裂面上内摩擦角及应力变化规律

本文采用的模型较理想弹塑性本构模型更能够真实地反映锚上拔破坏过程，破坏滑裂面上土体处于不同的应变状态，故沿滑裂面的应力比及土体强度不同，即滑动面上土体侧压力系数并非常值，内摩擦角亦非峰值内摩擦角。

3.1 滑裂面上内摩擦角变化

图6为自锚盘边缘开始沿破坏滑裂面上各单元的内摩擦角，其中

z

:

D

为各单元中点至锚盘的垂直距离与盘径之比。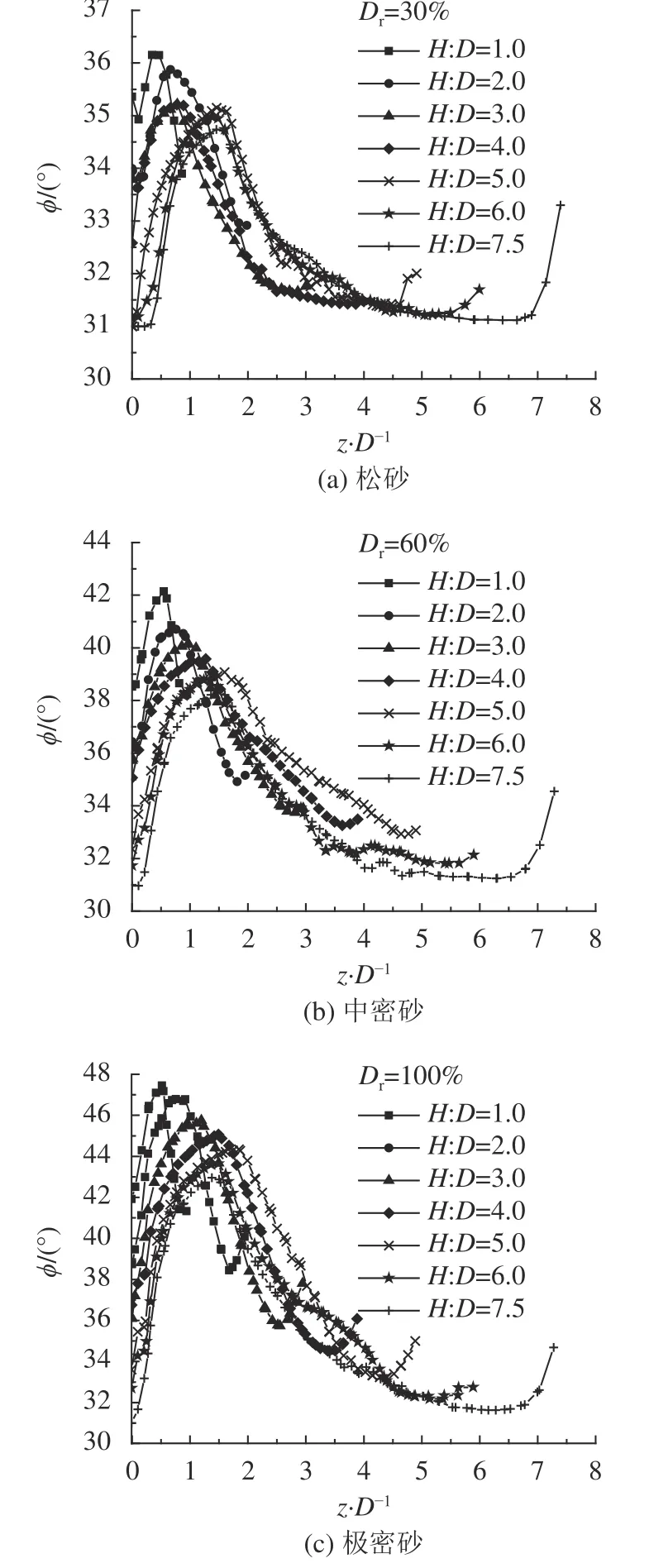

图6 破坏时滑裂面上内摩擦角分布Fig. 6 Distribution of friction angles along failure surface

由图6可见：从锚盘边缘开始内摩擦角逐渐增大至峰值内摩擦角，之后又开始减小，即滑裂面上土体强度发挥的程度不同；埋深越大，峰值内摩擦角的位置离锚盘越远。内摩擦角的发展规律与等效塑性应变相关，图5中盘边缘两侧剪切带一定高度范围的塑性应变超过2%，表明土体的强度经历了初始值至峰值的过程，进入强度降低的某个阶段，该区域内摩擦角小于峰值内摩擦角；对于较大埋深的锚，破坏时盘边缘等效塑性应变超过20%，内摩擦角进入临界状态内摩擦角，如松砂

H

:

D

≥5.0，中密砂和极密砂

H

:

D

=7.5。松砂在

H

:

D

≥5.0，中密砂

H

:

D

=7.5和极密砂

H

:

D

≥2时，在接近地表处滑裂面上的内摩擦出现异常增大，这是因为它们的理论滑裂面与数值滑裂面在接近地表处的偏差所致；偏差越大，内摩擦角异常增大越明显，如松砂

H

:

D

≥5.0，中密砂

H

:

D

≥6.0及极密砂

H

:

D

=7.5的过渡和深埋破坏情况。但对于过渡破坏的埋深，仅在靠近地表的很小范围内出现内摩擦角增大，且增量不超过3°，故对于过渡破坏模式，可采用浅破坏模式假设。

3.2 滑裂面上应力分布规律

提取沿滑裂面上各单元积分点的大小主应力，并根据各单元的内摩擦角值按Mohr-Coulomb平衡条件计算滑裂面上的法向应力σ及土压力系数

K

，

K

=σ/γ(

H

-

z

)，

z

为计算点至锚盘距离。将

K

以Hao等提出的土压力系数

K

进行标准化，获得了埋深范围内的标准化土压力系数

K

:

K

，如图7所示。自锚盘边缘起，侧压力系数

K

先近似呈线性增加至峰值

K

，而后非线性快速衰减至接近

K

值，这与Cerfontaine等基于硬土模型的数值模拟结果及Schiavon等利用光弹法测量透明土中上拔螺旋桩的应力规律相同，但峰值及峰值点的位置有所不同。

图7 滑裂面上标准化侧压力系数分布Fig. 7 Distribution of normalized coefficients of lateral pressure along failure surface

图8为不同密实度土中不同埋深比圆锚破坏滑裂面上的峰值土压力系数

K

，图9为不同埋深比时峰值点至锚盘距离与盘径比

z

:

D

及其与Cerfontaine等结果的对比。由图8可见，埋深比相对于土体密实度对

K

有更重要的影响；在埋深比较小时，

K

基本保持不变，之后，随着埋深比增加基本呈现线性增加；埋深比相同时，砂土密实度越小，土压力系数峰值

K

越大，这是由于土体越松，压缩性越高，拉拔过程中挤密程度越大，从而获得的土压力系数越大。与Cerfontaine等结果的对比发现，密实度相近的砂土，基于硬土模型的有限元分析获得的

K

基本上比本文采用软化模型获得的计算结果高，并且采用硬土模型的结果表现出土体密实度对

K

的影响比本文获得的密实度影响更大。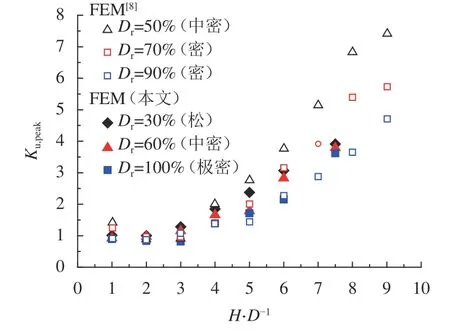

图8 侧压力系数峰值Ku,peak对比Fig. 8 Comparison of the peak lateral coefficients Ku,peak

图9 峰值侧压力系数对应的位置zp:D及对比Fig. 9 Comparison of the positions zp:D at peak lateral coefficients

由图9可见：Cerfontaine等获得的规律为，

z

:

D

明显受埋深比和相对密实度的影响，密实度越小，

z

:

D

越小；在较小埋深时，随着埋深比

H

:

D

增加，

z

:

D

线性增加至某一限值，而后保持不变，但

z

:

D

达到限值对应的埋深比与临界埋深比无关。而本文获得的

z

:

D

与埋深比

H

:

D

及密实度

D

的规律为，锚浅埋及过渡埋深时，峰值土压力系数位置

z

:

D

基本不受

H

:

D

和

D

的影响，即极密砂中

H

:

D

≤7.5，中密砂

H

:

D

≤6.0，松砂

H

:

D

≤5.0，

z

:

D≈

0.2；对于松砂深埋

H

:

D

=6.0、7.5及中密砂深埋

H

:

D

=7.5情况，

z

:

D≈

0.33。

4 理论计算

4.1 基于数值结果的极限上拔承载力

极限上拔承载力

Q

为滑裂面上法向应力σ及剪切强度 τ=σtan φ（φ为各单元上土体的内摩擦角）的竖向分量在滑裂面上的积分值

Q

与滑裂面内土体自重

W

（锚重按土重计算）之和，

Q

和

W

计算公式如式（2）和（3），其中，

Q

为滑裂面上各离散单元竖向抗力之和。

式中，γ′为土体有效重度，

H

为锚埋深，

D

为锚盘直径，ψ为峰值剪胀角，

K

为单元

i

上土侧压力系数，

z

和

z

分别为

i

单元上、下边界与锚盘的垂直距离，φ为

i

单元的内摩擦角。将不同密实度砂土中埋深比

H

:

D

≤7.5锚滑裂面上抗力

Q

及滑裂面内土重

W

计算结果列于表3。由表3可见：对于浅埋情况，松及中密砂，采用由假设滑裂面上提取的应力和内摩擦角数值结果计算的极限上拔承载力

Q

与数值模拟获得的

Q

误差在-10%～7%之间，表明浅埋假设的破坏滑裂面与实际情况基本一致；对于

D

=100%的情况（

H

:

D

≤7.5），

Q

与

Q

误差在-0.3%～15%之间，除

H

:

D

=1外，

Q

均大于

Q

，因为密砂中假设破坏滑裂面普遍偏大，尤其对于

H

:

D

=7.5过渡情况，见图5（c）。

表3 基于FEM结果的极限上拔力理论值和FEM结果对比
Tab. 3 Comparison between theoretical ultimate uplift resistance based on FEM and numerical results

Dr H:D Qτ1/kN式(2)W/kN式(3)Qu1/kN式(2)+(3)QuFEM/kN(模拟值)误差/%30%1.0 0.786 1.193 1.979 2.135 -7.323 2.0 3.725 3.091 6.816 7.581 -10.084 3.010.219 5.696 15.915 17.544 -9.285 4.024.034 9.027 33.061 34.367 -3.801 5.041.312 13.098 54.410 55.762 -2.425 6.075.034 17.920 92.954 78.409 18.550 7.5137.02 27.063 164.084 121.184 35.401 60%1.0 0.690 1.748 2.438 2.596 -6.076 2.0 3.521 5.346 8.867 9.360 -5.268 3.0 9.905 10.968 20.873 21.516 -2.985 4.022.141 18.755 40.897 41.638 -1.780 5.043.785 28.813 72.598 71.510 1.521 6.072.388 41.222 113.610 106.075 7.104 7.5110.71 64.370 175.081 158.159 10.699 100%1.0 0.440 2.958 3.399 3.409 -0.301 2.0 2.785 10.376 13.162 12.727 3.418 3.0 7.596 22.880 30.476 29.239 4.228 4.016.561 40.910 57.471 55.998 2.632 5.033.738 64.785 98.523 94.478 4.282 6.055.356 94.732 150.089 139.106 7.895 7.5103.585151.386254.970 221.950 14.877

对于深埋情况，由于采用浅埋破坏模式假设进行的计算，计算结果高于有限元结果，并且随着埋深增加，偏差越大，如

D

=30%，

H

:

D

=6.0和7.0情况，分别高估19%和35%，再次印证松砂

H

:

D

>5.0，中密砂

H

:

D

>6.0，已表现为深埋破坏模式。

4.2 浅埋锚极限上拔承载力理论公式及比较

4.2.1 等效内摩擦角

沿着破坏滑裂面土体塑性应变不同，土体强度被激发的程度则不同，部分土体处于峰值状态，部分土体强度经历峰值后开始下降或仍未达到峰值强度，沿滑裂面各单元内摩擦角并非常值φ。Davis等考虑土体非关联流动性或应变软化，采用式（4）计算极限荷载时破坏面（间断面）上的残余强度参数φ。

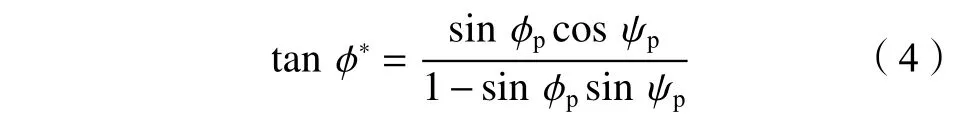
φ实际上为在利用极限分析法确定极限荷载时，考虑土体非关联流动性而在间断面上对土体内摩擦角进行的折减或考虑应变软化材料极限荷载时破坏面上的残余应力比。Drescher等指出对于承载力问题，采用该强度参数进行极限分析获得的理论值会低于基于非关联理想弹塑性本构模型的有限元分析结果，即意味着以理想弹塑性有限元计算获得的滑裂面上的应力比σ:σ应比由式（4）计算的结果高。

下面考察采用改进Mohr-Coulomb模型获得的浅埋锚滑裂面上的等效内摩擦角φ?与式（4）计算所得折减内摩擦角φ∗的关系。将滑裂面上实际变化的内摩擦等效为常值φ?，把φ?代入式（2）可计算Qτ1；反之，利用已经求和获得的Qτ1则可计φ?，如式（5），计算结果列于表4，同时将式（4）计算的折减内摩擦角φ∗列于表4进行对比。

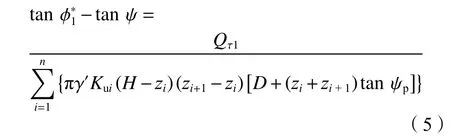
表4 等效内摩擦角及对比
Tab. 4 Equivalent friction angles and comparisons

Dr H:D φ∗1/(°)式(5)φ∗/(°)式(4) 误差/% φ∗φ∗(-)/(°)1 30%1.0 34.762 33.805 -2.753 -0.956 2.0 34.962 33.010 -5.583 -1.951 3.0 33.840 32.546 -3.824 -1.294 4.0 33.747 32.217 -4.534 -1.529 5.0 33.433 31.963 -4.397 -1.470 60%1.0 40.690 40.241 -1.103 -0.449 2.0 38.708 38.628 -0.207 -0.080 3.0 37.803 37.687 -0.307 -0.116 4.0 37.362 37.021 -0.913 -0.342 5.0 36.786 36.504 -0.767 -0.282 6.0 35.420 36.083 1.872 0.663 100%1.0 44.860 48.738 8.645 3.878 2.0 43.550 46.044 5.727 2.494 3.0 41.669 44.466 6.712 2.797 4.0 40.780 43.346 6.292 2.566 5.0 39.883 42.478 6.507 2.595 6.0 38.256 41.769 9.183 3.512 7.5 36.726 40.902 11.371 4.176

由表4可见：松砂条件，采用Davis的折减内摩擦角φ均低于考虑应变软化的有限元结果计算所得等效内摩擦角φ，对不同埋深比，平均低估1.4°；中密砂土中，φ与φ吻 合非常好；而对于密砂φ值 均高于φ，平均高估3.1°，主要是由于砂土密实度越大，应变软化现象越明显，从而滑裂面上等效内摩擦角与峰值内摩擦角相差越大。因此，采用式（4）估算滑裂面上的等效内摩擦角φ时，对于松及中密砂土，可以直接采用，而对于密砂，为安全起见，应在式（4）计算结果基础上减小3°左右。

4.2.2 侧压力系数

K

分布函数根据第3.2节分析的滑裂面上侧压力分布规律构造

K

函数，用于极限承载力理论分析。峰值前采用线性拟合，从某一值开始增加至

K

；峰值后，

K

非线性快速下降直至接近

K

，采用指数函数进行拟合。为简化，

z

=0的初始点

K

可按

K

取值，

K

如式（1）所示；对于浅埋情况，峰值点的位置

z

可统一取为0.2

D

。滑裂面上侧压力系数

K

的函数可表达成式（6），至此，确定变化函数的关键在于确定

K

值及指数衰减函数的参数

A

，

A

表示衰减速度，

A

越大，衰减越快。

式中，

k

为直线段斜率，

k

=(

K

-

K

)/

z

。图10为3种密实度砂土不同埋深比时峰值侧压力系数

K

/

K

。图11为3种密实度砂土中浅埋锚滑裂面上

K

的变化及拟合结果（实线），对于

D

=30%、60%、100%时，

A

值分别取为1.0、1.5、3.0。

图10 不同密实度土中不同埋深比时滑裂面上侧压力系数比Fig. 10 Normalized peak earth lateral pressure coefficient for different conditions

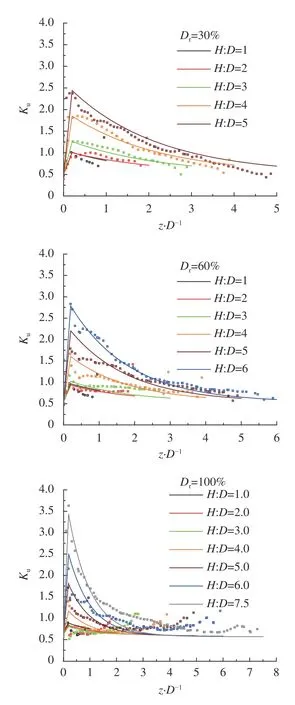
图11 土侧压力系数Ku拟合结果Fig. 11 Fitting results of lateral earth pressure coefficient Ku

4.2.3 理论公式计算结果

将滑裂面上等效内摩擦角表达式（4）及滑裂面上土应力分布函数（6）代入式（2），则滑裂面上土抗力

Q

可表达成式（7）～（9）：

对于过渡埋深的情况，由于假设的滑裂面比实际大会引起上拔力高估，松砂

H

:

D

=5.0，中密砂

H

:

D

=6.0，理论公式分别较数值计算结果高7.92%和7.17%。在这种情况，可以考虑采用下一等级密实度的侧压力衰减系数

A

进行计算，如对于松及中密砂过渡埋深情况，可取中密砂和密砂的

A

=1.5和3.0进行计算。表5为针对浅埋锚采用理论公式计算的极限上拔力

Q

及与有限元计算结果的比较，其中，松砂及中密砂过渡埋深计算时采用了上述

A

的取值方法。结果表明，对于不同密实度的砂土，通过直线-指数型函数表达的侧压力系数

K

计算的上拔承载力与数值模拟结果吻合较好。

表5 理论公式计算结果与有限元计算结果对比
Tab. 5 Comparisons between theoretical and numerical results

Dr H:D Qτ/kN式(8)+(9)W/kN式(3)Qu/kN式(8)+(9)+(3)QuFEM/kN(模拟值)误差/%30%1.0 0.817 1.193 2.010 2.135 -5.849 2.0 3.519 3.091 6.610 7.581 -12.809 3.010.033 5.696 15.729 17.544-10.345 4.024.317 9.027 33.344 34.367 -2.978 5.040.44413.098 53.542 55.762 -3.981 60%1.0 0.770 1.748 2.517 2.596 -3.019 2.0 3.420 5.346 8.766 9.360 -6.347 3.0 8.817 10.968 19.785 21.516 -8.045 4.022.22918.755 40.984 41.638 -1.570 5.043.44928.813 72.262 71.510 1.051 6.052.95241.222 94.175 106.075-11.219 100%1.0 0.419 2.899 3.318 3.409 -2.661 2.0 2.202 10.169 12.371 12.727 -2.793 3.0 5.783 22.422 28.205 29.239 -3.539 4.013.30840.092 53.400 55.998 -4.638 5.026.33163.489 89.820 94.478 -4.930 6.044.90792.837 137.744 139.106-0.979 7.581.955148.358 230.313 221.950 3.768

采用Hao等和Giampa等的理论公式及Cerfontaine等基于FEM结果的理论方法估算本文有限元算例。前两个理论公式的差别在于采用了不同的侧向土压力系数公式及是否考虑非关联法则的影响。对任意密实度砂土中的浅埋锚极限上拔承载力，Giampa等结果比Hao等结果高约20%～35%，埋深越大，两者结果相差越大。图12为浅埋锚极限上拔承载力不同计算公式的误差对比。其中，由于文献[8]中仅给出相对密实度

D

=50%～90%时侧压力系数图，因此，对于松砂的算例，未采用Cerfontaine等理论方法计算，对于

D

=60%的算例，侧压力系数插值确定，对于

D

=100%的算例，采用

D

=90%的侧压力系数计算。

由图12可见：松砂时Giampa等和Hao等理论公式均低估锚的上拔承载力，低估量范围分别在-4%～-23%、-51%～-25%，基于本文FEM结果的理论公式估算相对较好；对于中密砂，Giampa等和本文基于FEM的理论公式估算结果较好，误差在-11%～6%之间，而Hao等结果仍低估锚上拔承载力-13%～-34%，Cerfontaine等结果高估承载力16%～60%；对于密砂，Hao等及本文基于FEM的理论公式计算结果误差在-5～7%以内，而Giampa等结果高估了16%～32%，Cerfontaine等结果则高估了19%～105%，且埋深越大误差越大，主要由于Giampa等和Cerfontaine等高估了密砂中滑裂面附近土体的侧压力，且未考虑应变软化带来的土体强度降低。

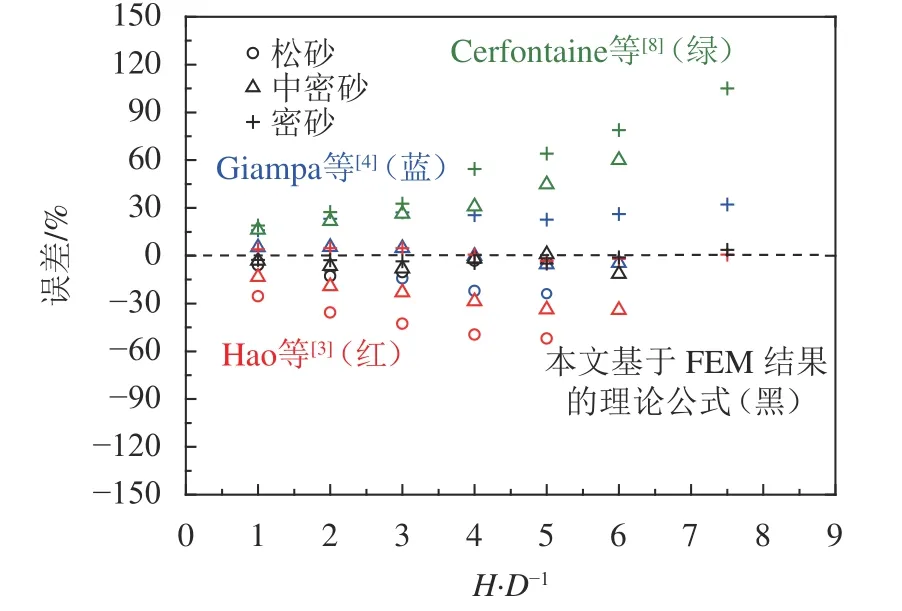
图12 浅埋锚极限上拔承载力不同计算公式误差对比Fig. 12 The errors of different formulas for ultimate uplift capacity of shallow circular anchors

综上，从安全和经济的角度，砂土中浅锚上拔承载力计算可采用本文基于FEM结果的理论方法计算不同密实度的情况，但计算相对繁琐；亦可采用Giampa等和Hao等公式，建议当为松砂和中密砂时，采用Giampa等公式计算，内摩擦角不折减；当为密砂时，采用Hao等公式计算，并考虑内摩擦角的折减。

5 结 论

本文利用Abaqus中3维欧拉大变形有限元分析方法，同时采用能够考虑应变软化的改进Mohr-Coulomb模型对圆锚拉拔过程进行数值模拟。通过与离心机试验结果进行对比，验证了数值模型的有效性，进而探讨了不同密实度砂土中锚的拉拔破坏机理，并基于数值分析结果提出了浅埋圆锚或螺旋锚上拔承载力理论公式，同时对比分析已有的理论计算公式，建议各公式的适用条件，为工程应用提供参考。具体结论如下：

1）随着埋深增加，锚周围土体的破坏模式不同，从浅埋时的倾斜角度接近于剪胀角的倒锥台型滑裂面向底部臌胀顶部渐缩的曲面型过渡模式发展。对于松砂、中密砂和极密砂，埋深比

H

:

D

分别小于等于4.0、5.0、6.0时发生浅埋破坏模式；松砂和中密砂，当

H

:

D

分别大于6.0和7.5时会发生深埋破坏模式；当

H

:

D

=7.5时极密砂仍为过渡破坏模式。2）对于浅埋及过渡埋深比时，破坏滑裂面均可按直线表示，沿着滑裂面土体侧压力系数

K

并非常值，自锚盘边缘到地表，呈先线性增加至峰值

K

，而后近似以指数形式衰减至稳定值；埋深比相对于土体密实度对

K

有更重要的影响；

K

位置基本不受

H

:

D

和

D

的影响，

K

衰减速率明显受密实度影响，密实度越高，衰减越快，

K

最后的稳定值接近Hao等提出的土侧压力系数。

3）上拔破坏时，沿着滑裂面上，自锚盘边缘开始内摩擦角逐渐增大至峰值内摩擦角，之后又开始减小。当进行极限平衡分析时，采用等效内摩擦角φ将滑裂面上变化的内摩擦角以常值表示，对中密砂土，φ满足Davis等提出的内摩擦角折减公式；对于松砂，Davis等公式略低估φ；而对于极密砂，该公式高估φ约3°。

4）通过各理论计算方法的比较，表明，对于任意密实度砂土中浅埋圆锚或螺旋锚，采用本文基于FEM的理论公式计算极限上拔承载力，既安全又经济，但计算相对繁琐；亦可采用Giampa等和Hao等公式，建议当为松砂和中密砂条件时，采用Giampa等公式计算，内摩擦角不折减；当为密砂时，采用Hao等计算公式，并考虑内摩擦角的折减。

致谢：感谢中国海洋大学王栋教授和郑敬宾副教授为本研究提供相关程序。