一种基于时间-频率特征分析的自适应信道化技术*

匡宏印

(中国西南电子技术研究所，成都 610036)

0 引 言

现代战场电磁环境十分复杂，对电子战接收机的瞬时频率覆盖范围、灵敏度、动态、分辨率等指标提出了很高的要求。特别是随着雷达信号调制方式日益复杂化，信号密度不断提高，时空频域交叠越来越严重，对电子战接收机的多信号分离能力提出了特别的要求。文献[1]介绍的基于多相滤波结构的信道化接收机，通过对算法多相分解大幅度降低计算资源需求，但其均匀划分子信道带来了宽带信号分裂、跨信道重复检测等问题。文献[2]通过设置奇偶两组交叉的信道化滤波器组，解决了单信号环境下信号跨信道重复检测问题，但在多信号环境下效果不佳，并且无法解决宽带信号分裂问题。文献[3-4]提出了基于快速傅里叶变换(Fast Fourier Transform，FFT)结构的数字信道化接收机设计方法，利用FFT运算代替多相滤波完成信道化过程，实现对常规雷达信号的处理，但其运算量随着级联级数的增加而增加，并且无法适应信号跨信道分布的情况。针对以上传统信道化技术的缺点，近年来基于分析与综合技术的先进数字信道化接收机(Advanced Digital Channelized Receiver，ADCRx)成为研究的新方向。文献[5]提出了基于多相滤波结构的分析与综合信道化算法，能够解决信号跨道分布问题，但是存在计算量大、信号重建过程复杂、多信号分离能力不佳等问题。

本文基于先进数字信道化接收机(ADCRx)设计思想，提出一种信道化新技术，基于时间-频率特征分析[6]，通过二维聚类方法分离跟踪多信号，自适应动态调整子信道划分并对信号进行重建，实现高信号密度条件下对宽带复杂调制信号的完整截获。

1 信号时-频分析

从模数转换器(Analog-to-Digital Converter，ADC)采集到的数字脉冲序列可表示为

(1)

式中：s(n)表示信号序列，η(n)表示噪声序列，Ω(s)表示存在信号的区域。令

(2)

则序列x(n)的N点离散傅里叶变换(Discrete Fourier Transform，DFT)结果X(k)为

X(k)=x(n)*hk(n)=

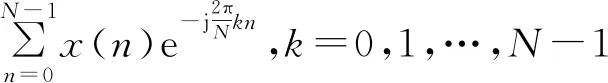
(3)

产生两个加噪脉冲信号，信号1为脉宽30 μs的简单脉冲，信号2为脉宽20 μs、带宽10 MHz的线性调频信号，信噪比设定为15 dB。两个信号在时域上有交叠，频域上分开，时域波形和频谱如图1所示。可见，时间上重叠的两个信号虽然不能在时域上做出区分，但变换到频域后却能方便地区分开来。然而信号频谱却不能提供时间相关参数，即丢失了时间参数的测量分析能力，无法测量信号的脉冲到达时间(Time-of-Arrival，TOA)、脉冲宽度(Pulse Width，PW)等参数。现代信号分类算法中，都希望这两个参数有很高的时间分辨率。

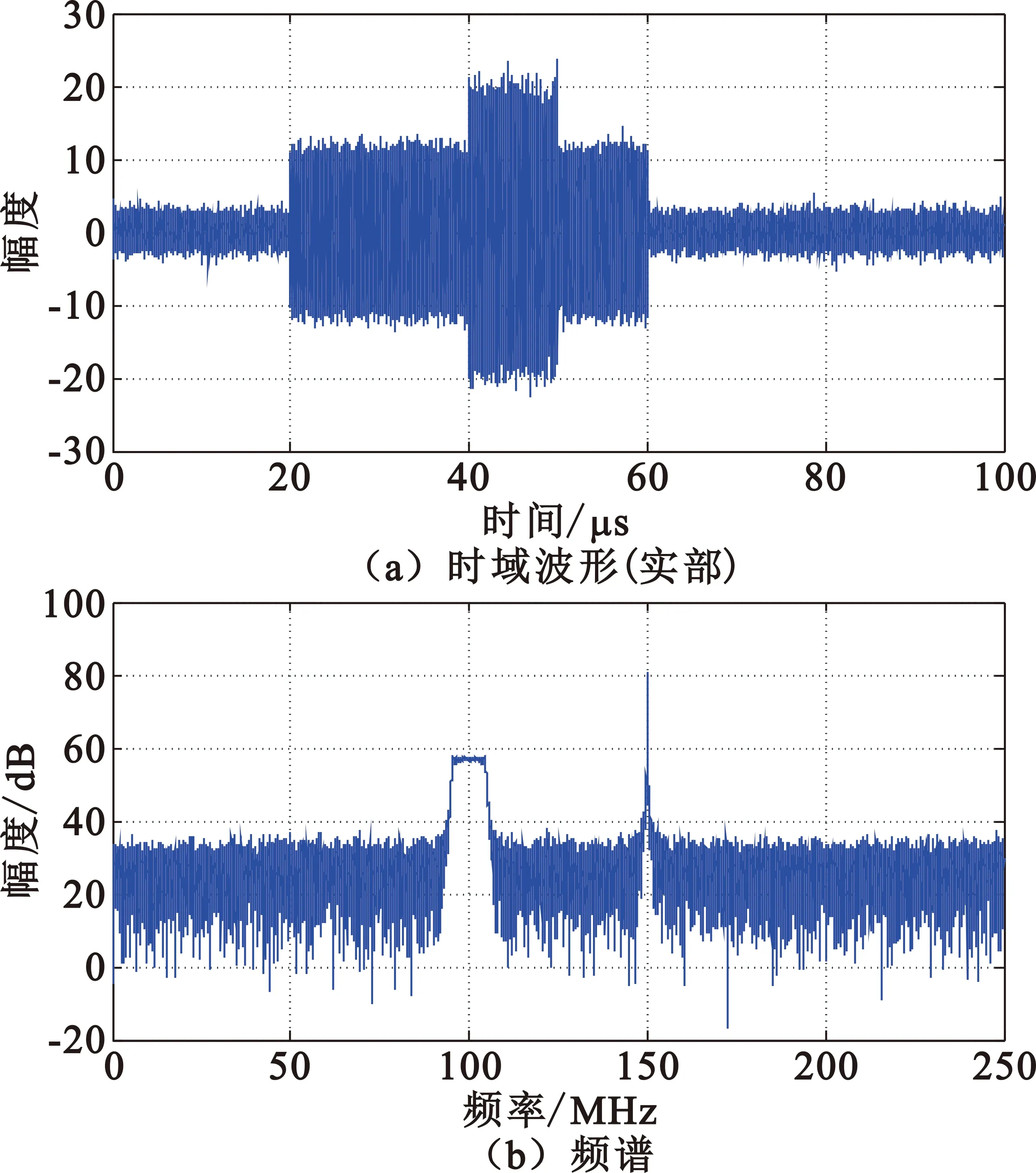
图1 信号时域波形和频谱

借鉴短时傅里叶变换(Short-Time Fourier Transform，STFT)思想[6]，对N点输入信号不再直接做N点离散傅里叶变换，而是分段每隔L点(1≤L≤N)做一次L点离散傅里叶变换。这样处理可以获得时间参数分辨能力。具体提升程度与L的取值有关，若L取1，时间参数分辨率等同于ADC原始采样率；若取L，则时间分辨率降低到原始采样率的1/L。L取值同样影响信号的频域分辨能力，L取值越小频域分辨率越低。当L取1时虽然获得了最高的时间分辨率，但同时也丧失了频率分辨能力，无法分离时间上重叠的信号。在这种处理方式下，时间分辨率和频率分辨率的提升是一对矛盾体，无法兼得。

考虑相邻两次离散傅里叶变换之间重叠部分数据，即每隔L点(1≤L≤N)做一次M点(L≤M≤N)的离散傅里叶变换[7]。将时间分辨率与频率分辨率解耦合，那么可以得到两种分辨率都足够高的处理方法。分段DFT表达式为

(4)

式中：x(n)为输入信号序列；L为每次处理滑动的点数；p=0,1,…,N/L-1为分段处理的时间索引，可以理解为分段处理的二次重采样离散采样时刻点；k=0,1,…,M-1代表离散数字频率；X(p,k)代表第p组采样数据中，第k个频率通道输出的频域信号。随着输入采样序列x(n)的变化，M个频率通道输出的频域信号共同构成了输入信号在对应时间内的频谱分布。下一次处理开始前，采样序列x(n)向后滑动L点，再得到新的M点频谱信息。如此持续下去就能得到信号频谱随时间变化的规律，即具备了时间-频率两个维度分析能力。

对图1所示信号进行分段DFT处理，选取四种参数，其中参数1的M=8 192、L=8 192，参数2的M=4 096、L=1 024，参数3的M=1 024、L=256，参数4的M=128、L=1，结果如图2所示。

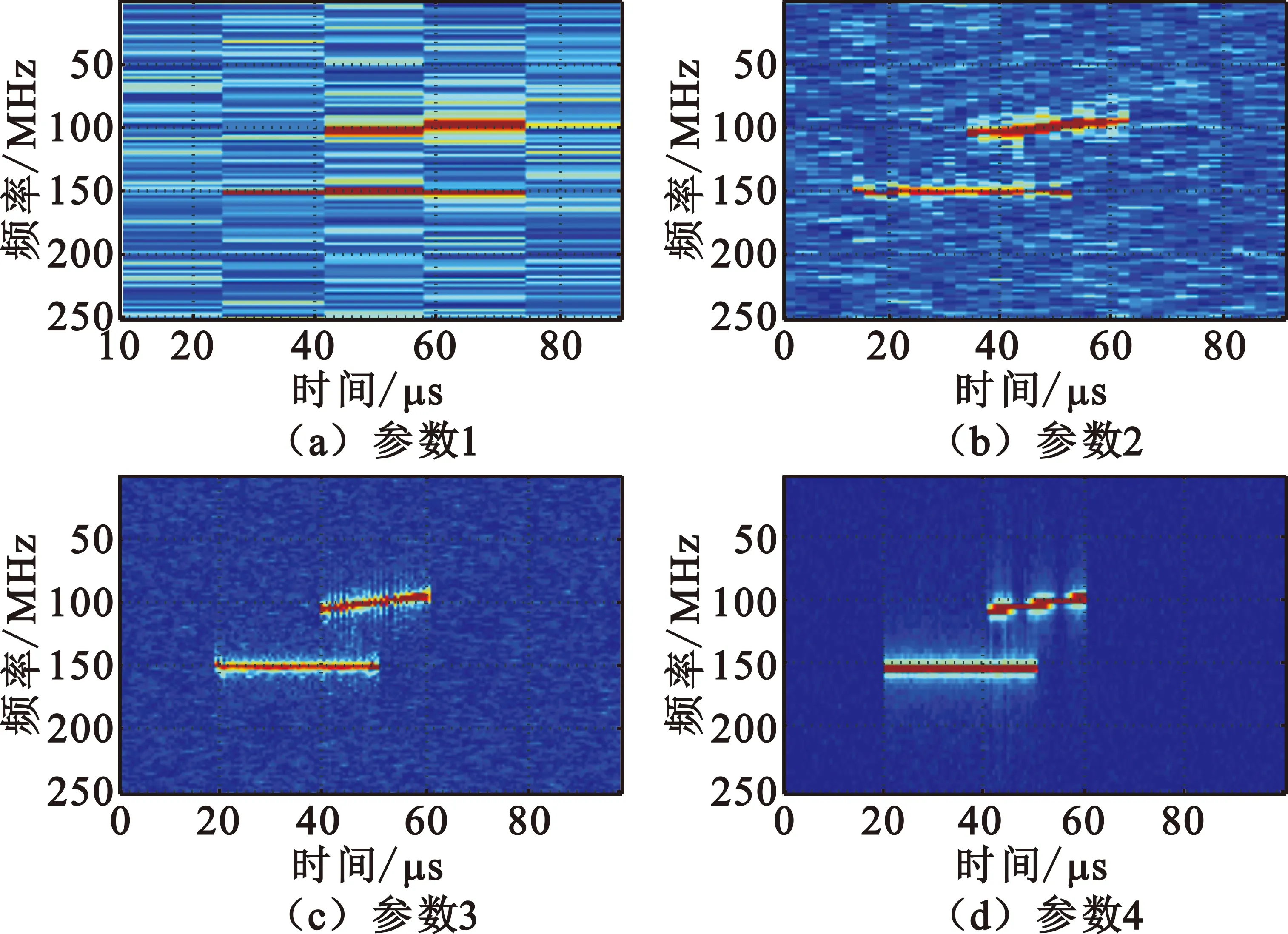
图2 信号时间-频率分析结果

从图2中可见，当选取DFT点数(M)越大，得到的频率分辨率越高；选取的时域滑动点数(L)越小，得到的时间分辨率越高。理想情况下希望M值尽量取大(例如1 024)，L值最好取1，然而这样选取信道化参数会导致计算资源的极大消耗，难以在FPGA中实现。

分析式(4)，当L=1，即每次只向后滑动一个采样点的情况，此时计算分段DFT表达式，滑动到p点采样数据为{x(p-M+1),x(p-M+2),x(p-M+3),…,x(p-1),x(p)}，DFT计算表达式为

(5)

当滑动到p-1点采样数据为{x(p-M),x(p-M+1),x(p-M+2),…x(p-2),x(p-1)}，DFT计算表达式为

(6)

比较式(15)和式(16)，有

(7)

由式(7)可见，对于逐点滑动DFT，第p点的结果可由第p-1点的结果很方便地获得。当前DFT运算输出只决定于当前的输入采样点数据x(p)、前一次DFT运算结果X(p-1,k)和与本次运算无关需要丢弃的采样点数据x(p-M)，计算量较小，便于FPGA实现。FPGA中递归实现结构如图3所示[7]。

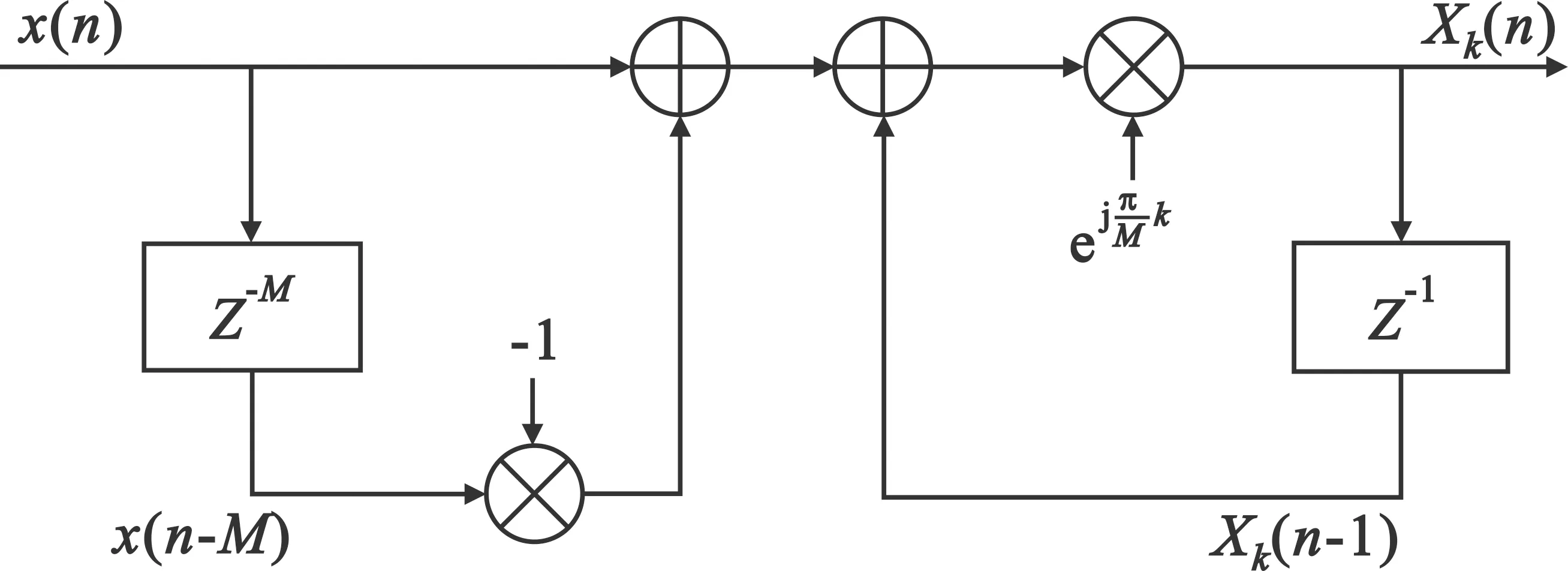
图3 滑动DFT FPGA实现结构

采用递归方式计算逐点滑动DFT，量化截断误差累积会导致递归表达式不稳定，需要进行修正[8]。另外由图2信号时间-频率分析结果可见，DFT运算结果存在频谱泄露问题。对于该问题，通常可在时域对输入数据加窗解决。然而由式(4)和式(5)可知，对输入数据加窗会破坏其递归特性，无法再得到表达式(7)。时域加窗和频域卷积运算是等效的，可以考虑在频域将X(p,k)与窗函数作卷积从而完成加窗运算[9]。第p点的加窗计算表达式为

Xwin(p,k)=X(p,k)*W(k)=

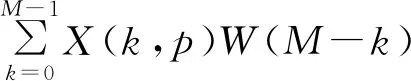
(8)

在FPGA中可通过FIR滤波器高效实现。

2 二维跟踪滤波

将加窗(Hanning窗)的逐点滑动DFT结果，如图4(a)所示，按频率通道号k分别求模，得到M组时间-频率幅度；再将得到的幅度与门限做比较，并在频率维合并相邻通道只保留峰值，得到时-频检测结果，如图4(b)所示。信号的时-频检测结果描述了信号随时间变化其频率成分的变化趋势。利用这种二维变化规律，不但可以分离时间和频率重合的多个信号，而且可以根据每种信号调制方式的具体时-频变化规律对其进行识别跟踪。对跟踪到的属于某一信号的频率信息进行反变换，就能得到该信号完整的时域波形，实现多信号分离，提高信噪比。下面以几种常见的脉冲雷达信号调制方式为例来对此进行说明，相关参数最大幅度差ΔAmax、最大频率差Δfmax、最小频率差Δfmin、最长中断时间Δtmax等需要根据具体工程实践进行设置。

图4 信号滑动SDFT和时-频检测结果

线性调频(Linear Frequency Modulation，LFM)信号其频率随时间线性变化，如图5(a)所示，利用这个特点可对其进行识别跟踪。以下几个准则判断信号是否属于同一个线性调频信号：

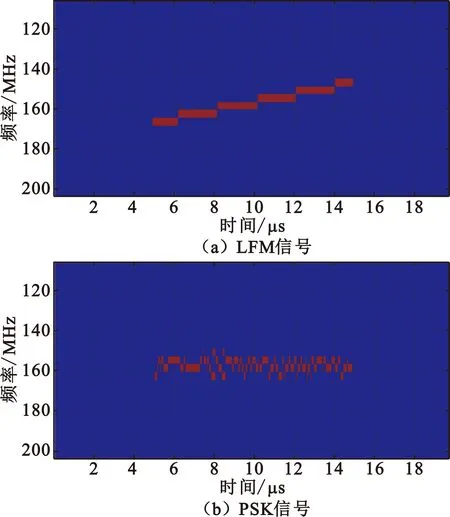
图5 几种调制类型脉冲信号时-频检测结果

(1)当前时刻信号幅度与前一时刻信号幅度差不大于ΔAmax;

(2)当前时刻信号频率与前一时刻信号频率差小于Δfmax；

(3)信号的频率变化率Δf/Δt为一常量；

(4)在信号持续范围内时域和频域没有中断。

相位编码(Phase Shift Keying，PSK)雷达脉冲信号如图5(b)所示，可以通过以下几个准则进行跟踪：

(1)当前时刻信号幅度与前一时刻信号幅度差不大于ΔAmax;

(2)在信号持续时间内其频率不是固定的；

(3)信号如果发生频率变化，每次变化量Δf与本信号最小频率变化量Δfmin没有倍数关系；

(4)信号的频率变化率Δf/Δt不是常量；

(5)在信号持续范围内时间上基本保持连续(间断时间不大于Δtmax)。

对新出现的信号，实时统计其频率、频率变化率、幅度等特征参数，按照上文介绍的准则判断信号归属的类型，并对下一时刻信号可能出现的频率范围做出预测。若下一时刻出现多个频率值，则按照每个信号各自预测范围做匹配，即使两个信号某一时刻在频率上有重合，也可利用其频率变化率、幅度等特征参数的差异对其作区分。

利用以上策略对信号时-频检测结果进行判断、跟踪、合并，得到单个完整信号在其持续时间内的频率通道号(idx)信息。丢弃掉与本信号无关的频率成分，只需将频率通道号(idx)及其左(idx-1)右(idx+1)两个通道进行反变换，就能得到时-频滤波后的时域信号。反变换公式为

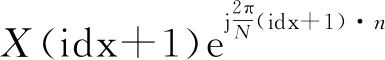
(9)

式中：idx为跟踪到的频率通道号，其是随时间n(n=0,1,…,N-1)动态变化的;X(k)为由式(7)得到的滑动DFT第k个频率通道值。由上式可见，只需将得到的各频率通道对应的幅度值与数字本振信号相乘后再相加就能得到时域波形，算法所需资源很少，便于FPGA实现。

3 信道化方案

基于时间-频率特征分析的自适应信道化技术FPGA实现结构如图6所示，算法实现步骤如下：

图6 信道化结构

Step1 对信号做数字下变频(Digital Down Converters，DDC)得到正交复信号x(n)。

Step2 根据式(7)计算x(n)的逐点滑动DFT值X(p,k)。

Step3 根据式(8)计算X(p,k)的加窗值Xwin(p,k)。

Step4 计算Xwin(p,k)的模值|Xwin(p,k)|。

Step5 对得到的模值进行信号检测、合并、跟踪得到有效信道号idx。

Step6 根据信道号idx按照式(9)进行反变换得到输出时域信号y(n)。

4 仿真实验

为验证算法有效性，产生如下三个时域和频域有重叠的脉冲信号进行仿真，信号采样频率设定为500 MHz：信号1为脉宽15 μs、频率377 MHz的简单脉冲；信号2为脉宽30 μs、带宽40 MHz、中心频率375 MHz的线性调频信号；信号3为脉宽20 μs、带宽6 MHz、中心频率415 MHz的相位编码信号，信噪比15 dB。信号间的时间和频率重叠关系如图7所示。

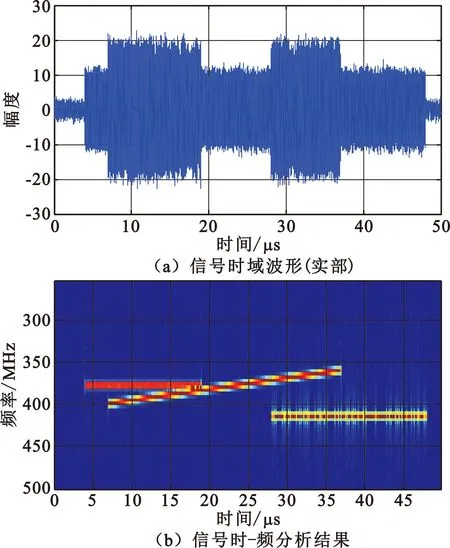
图7 信号时域波形和滑动DFT结果

首先对产生的混叠信号进行数字下变频处理，数字本振信号选取为375 MHz，再使用本文算法进行信道化处理，输出结果如图8所示。可见，在时间和频率上都重叠的三个不同调制类型雷达信号，能正确地从各子信道输出，并且子信道可以跟随信号频率的变化做自适应调整，输出信号在子信道调整时依然保持正确的相位关系。

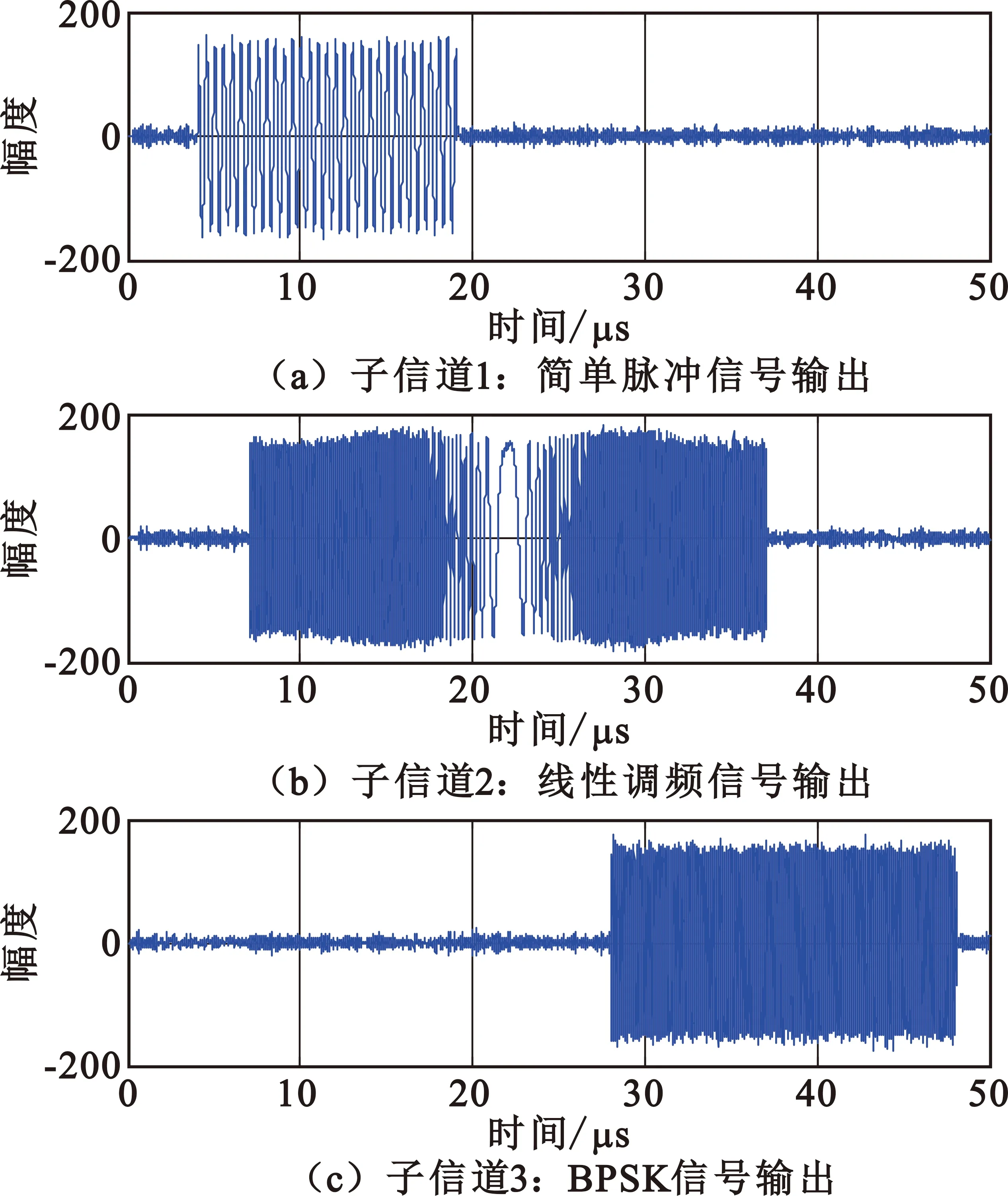
图8 子信道信号分离输出结果

对于传统信道化技术，当时间上有交叠的多个信号在频率上也相差不大时(频率差小于子信道带宽)，无法有效分离多个信号。解决方法通常是增加信道数、减小子信道带宽，这样不但会带来计算资源大幅度增加，面对宽带低截获雷达信号(LFM、PSK等)，还会造成严重的信号分裂和重复检测，影响后续信号参数测量、分选和识别。本文算法基于信号的时-频特征分析，即使多个信号存在时间和频率交叠，也能利用不同信号时-频变化趋势的差异将其分离开，并且子信道可以自动匹配对应信号，做到子信道号和子信道宽度的自适应调整，不会造成宽带信号分裂和重复检测。

5 FPGA实现

在Xilinx公司Virtex7系列FPGA芯片上实现本信道化算法，开发环境为vivado 2016.4，芯片型号为xc7vx690tffg1927-2，开发语言VHDL，FPGA资源使用情况如表1所示。

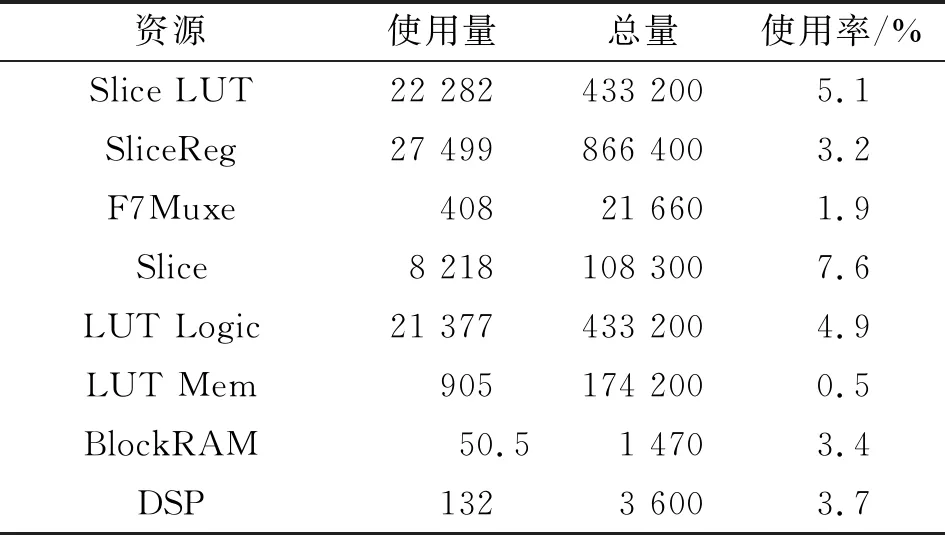
表1 FPGA实现资源使用情况统计表

输入时间和频率上有重叠的三个雷达脉冲信号，其信号形式分别为简单脉冲、线性调频信号和相位编码信号，经过FPGA数字下变频和信道化模块处理后输出如图9所示。由图可见，本文所提信道化算法不但能正确分离多个时-频重叠的脉冲信号，而且资源需求量低，具有很好的工程实用价值。

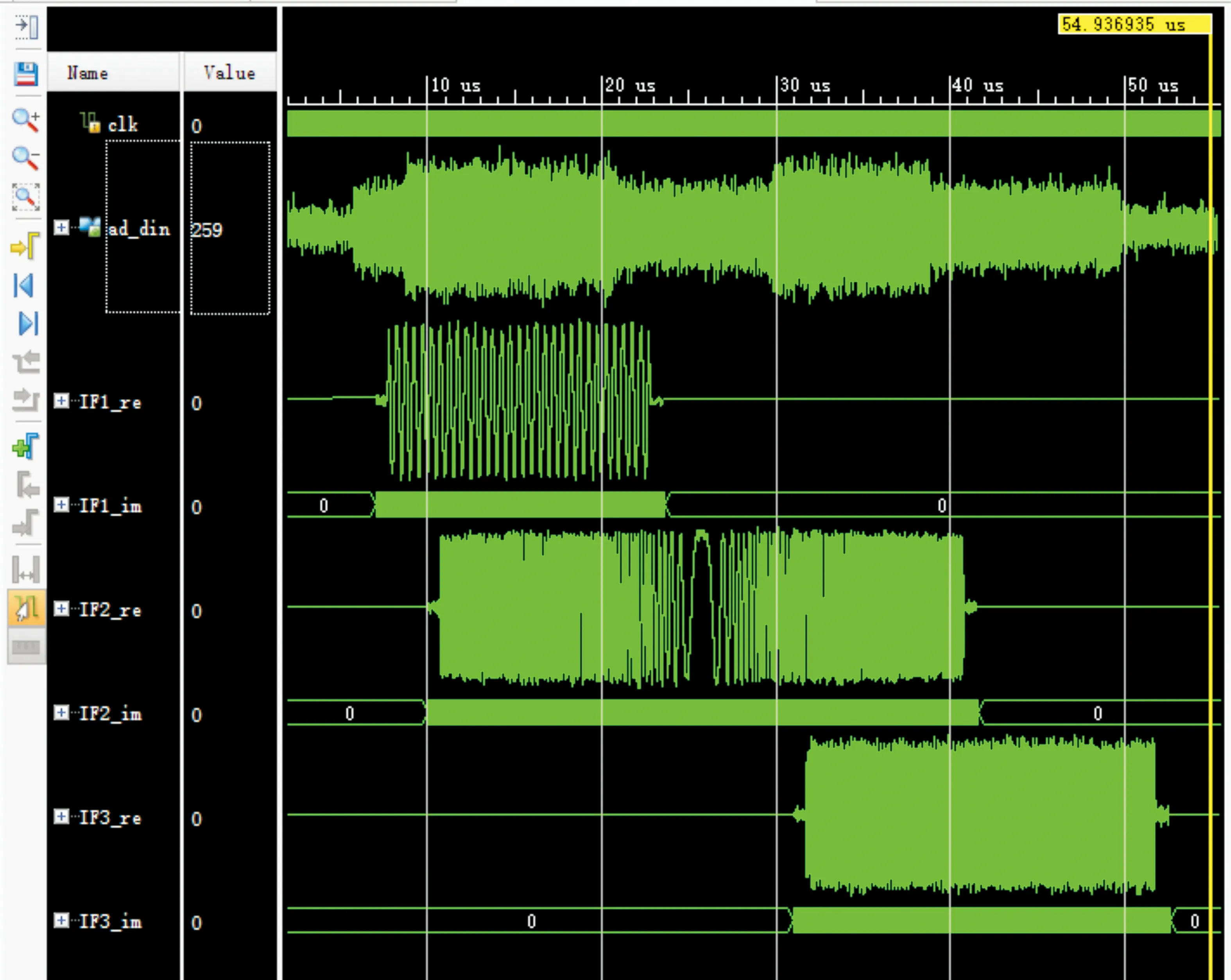
图9 FPGA仿真波形

6 结束语

针对传统数字信道化技术面临的问题，本文提出了一种基于信号时间-频率特征分析的自适应信道化技术，根据不同信号的时-频特征变化趋势，自适应动态分配、组合子信道，反变换后输出截获的完整时域信号，解决信号重复检测、分裂等问题，无需抽取，不降低信号的时间分辨率，有利于对信号进行细微指纹特征分析，并且运算复杂度较低，适用于FPGA等硬件的实现，具有较强的工程实用价值。

当前子信道跟踪预测部分使用常规方法，后续需要研究利用人工智能等最新技术手段的低延迟、低资源开销跟踪预测算法，构建更加智能化的信道跟踪结构，进一步提升算法性能。