注重函数性质交汇 明晰函数图象判别

黄雅兰

摘 要：本文主要紧扣函数的性质，研究了函数的图象变换、函数的应用和函数的识别问题.

关键词：函数性质;函数图象;图象变换

中图分类号：G632   文献标识码：A   文章编号：1008-0333（2022）04-0024-03

基本初等函数的性质是高考试题中最为常考的一种题型之一，通过函数图象去研究函数性质是数学方法中常见的一种研究手段，本文立足函数性质，分析了函数图象的相关问题.

1 函数性质的综合应用

例1 已知f （x）是定义在

R上的奇函数，且f（x+1）为偶函数，若f（-1）=2，则f（1）+f（2）+f（3）+…+f（2019）=（  ）.

A.4  B.2  C.0  D.-2

解法1 f（x）是定义在R上的奇函数，

所以-f（x）=f（-x）.①

因为f（x+1）为偶函数，

所以f（-x+1）=f（x+1）.②

在②式中，用x+1替代x，

则f（-x）=f（x+2）.

所以f（x）=-f（x+2）.③

在①式中，令x+2替代x，

则-f（x+2）=f（-x-2）.④

因为f（-x-2）=f[-（x+3）+1]，

再根据②式关系，得

f（-x-2）=f[-（x+3）+1]=f[（x+3）+1]=f（x+4）.

综上所述，得f（x）=f（x+4）.

所以f（x）的周期为4.

由已知得，f（x）是定义在R上的奇函数，

则

f（0）=0，f（1）=-f（-1）=-2，

f（2）=f（1+1）=f（-1+1）=f（0）=0，

f（3）=f（-1+4）=f（-1）=2，

f（4）=f（0+4）=f（0）=0，

所以f（1）+f（2）+f（3）+f（4）=0.

所以f（1）+f（2）+f（3）+f（4）+…+f（2019）

=504×[f（1）+f（2）+f（3）+f（4）]+[f（1）+f（2）+f（3）]=-2+0+2=0.

解法2 由f（x）是定义在R上的奇函数，且f（x+1）为偶函数，可知函数f（x）是周期为4的周期函数.

又f（-1）=2，取f（x）=-2x，x∈[-1，1]，

则f（1）=-2，f（2）=f（0）=0，f（3）=f（-1）=2，f（4）=f（0）=0.

所以f（1）+f（2）+f（3）+f（4）+…+f（2019）=504×[f（1）+f（2）+f（3）+f（4）]+[f（1）+f（2）+f（3）]=-2+0+2=0.

点评 已知f（x）是周期函数且为偶函数，求函数值常利用奇偶性及周期性进行交换，将所求函数值的自变量转化到已知解析式的函数定义域内，把未知区间上的函数性质转化为已知区间上的函数性质求解.

2 函数图象的识别

例2 （2021年安徽池州模拟）如图1，函数f（x）=

xln2-sinx2+sinx的部分图象可能是（  ）.

解析 因为f（x）=xln2-sinx2+sinx，

故f-x=-xln2+sinx2-sinx=-xln2-sinx2+sinx-1=xln2-sinx2+sinx=fx，

所以f（x）是偶函数.

所以f（x）的图象关于y轴对称，故排除C，D.

当x∈0，π2时，sinx∈0，1，

所以0<2-sinx2+sinx<1.

所以ln2-sinx2+sinx<0.

即f（x）<0，故排除B，选A.

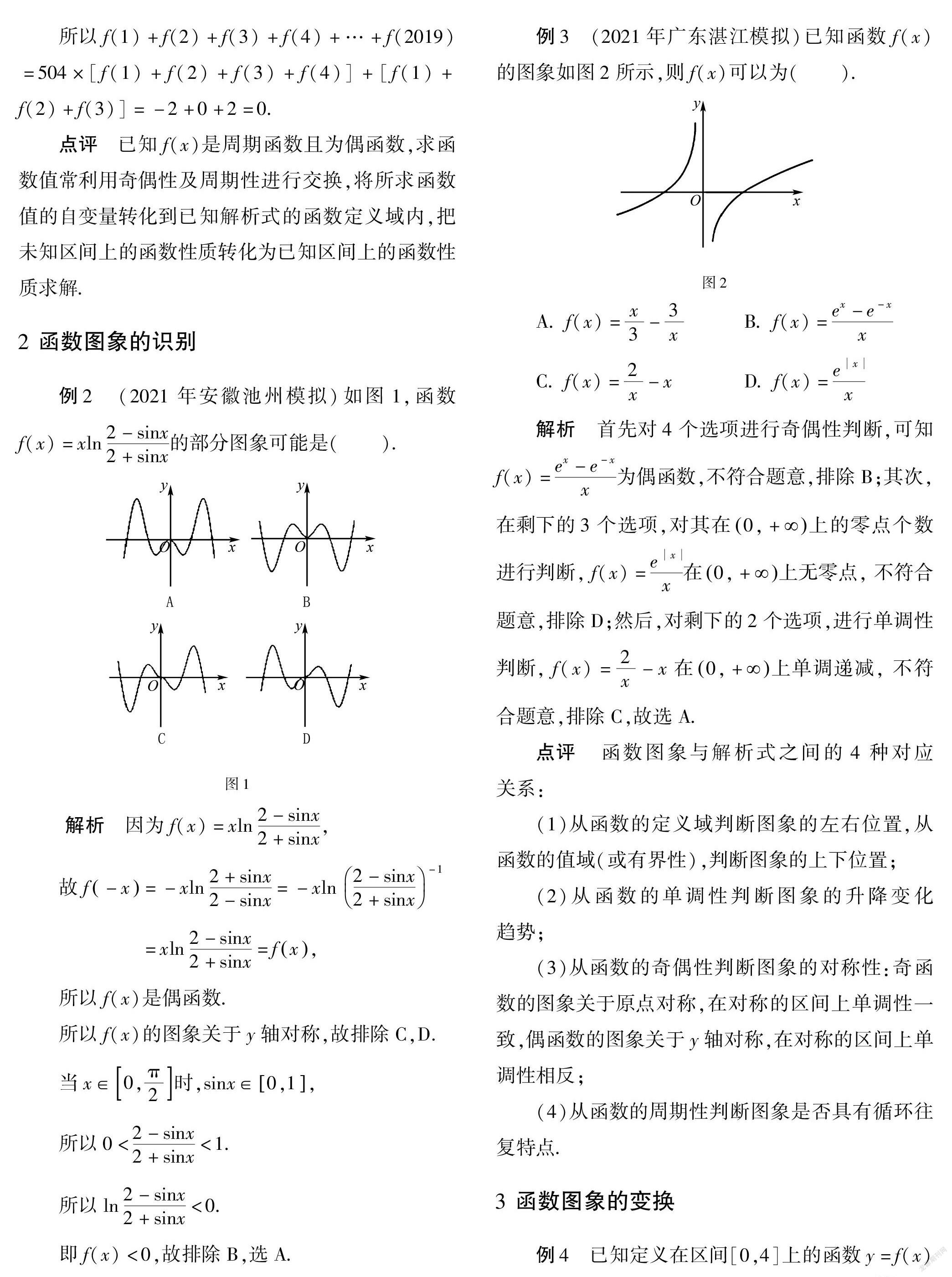
例3 （2021年广东湛江模拟）已知函数f（x）的图象如图2所示，则f（x）可以为（  ）.

A. f（x）=x3-3x   B. f（x）=ex-e-xx

C. f（x）=2x-xD. f（x）=exx

解析 首先對4个选项进行奇偶性判断，可知f（x）=ex-e-xx为偶函数，不符合题意，排除B;其次，在剩下的3个选项，对其在0，+SymboleB@上的零点个数进行判断， f（x）=exx在0，+SymboleB@上无零点， 不符合题意，排除D;然后，对剩下的2个选项，进行单调性判断， f（x）=2x-x在0，+SymboleB@上单调递减， 不符合题意，排除C，故选A.

点评 函数图象与解析式之间的4种对应关系：

（1）从函数的定义域判断图象的左右位置，从函数的值域（或有界性），判断图象的上下位置;

（2）从函数的单调性判断图象的升降变化趋势;

（3）从函数的奇偶性判断图象的对称性：奇函数的图象关于原点对称，在对称的区间上单调性一致，偶函数的图象关于y轴对称，在对称的区间上单调性相反;

（4）从函数的周期性判断图象是否具有循环往复特点.

3 函数图象的变换

例4 已知定义在区间[0，4]上的函数y=f（x）的图象如图3所示，则y=-f（2-x）的图象为（  ）.

解法1 先作出函数y=f（x）的图象关于y轴的对称图象，得到y=f（-x）的图象;然后将y=f（-x）的图象向右平移2个单位，得到y=f（2-x）的图象;

再作y=f（2-x）的图象关于x轴的对称图象，得到y=-f（2-x）的图象.故选D.

解法2 先作出函数y=f（x）的图象关于原点的对称图象，得到y=-f（-x）的图象;然后将y=-f（-x）的图象向右平移2个单位，得到y=-f（2-x）的图象.

故选D.

点评 通过图象变换识别函数图象要掌握的两点：

（1）熟悉基本初等函数的图象（如指数函数、对数函数等函数的图象）;

（2）了解一些常见的变换形式，如平移变换、翻折变换.

4 函数图象的应用

例5 已知f（x）=lgx，x>0，2x，x≤0，则方程2f 2（x）-3f（x）+1=0的解的个数为.

解析 方程2f 2（x）-3f（x）+1=0的解为f（x）=12或f（x）=1.

如图5，作出y=f（x） 的图象，由图象知直线y=12与函数y=f（x）的图象有2个公共点;

直线y=1与函数y=f（x）的图象有3个公共点.

故方程2f 2（x）-3f（x）+1=0有5个解.

点评 利用函数图象可以解决很多与函数有关的问题，如利用函数的图象解决函数性质问题，函数的零点、方程根的问题，有关不等式的问题等，当方程与基本函数有关时，可以通过函数图象来研究方程的根，方程f（x）=0的根就是函数f（x）图象与x轴交点的横坐标，方程f（x）=g（x）的根就是函数f（x）与g（x）图象交点的横坐标.

参考文献：

[1] 蓝云波，陈国林.导数问题中运用零点存在定理的赋值策略探究[J].中小学数学（高中版），2016（10）：54-57.

[2] 廖永福.高考考查函数图象的三个视角[J].数理化解题研究，2020（13）：20-23.

[责任编辑：李 璟]