基于粗糙数据集的水库移民安置区选择规划方法

黄 毅

(贵州省水利水电勘测设计研究院有限公司，贵阳 550002)

0 引 言

中国具有丰富的水能资源，其蕴藏量居世界首位。自改革开放以来，中国水利水电行业发展迅速，获得巨大的成就，改善了国内能源结构，缓解了结构性缺水问题，在保障社会稳定基础上，极大地推动了中国经济的飞速上涨。近十几年，中国已经修建了80 000座以上的水利大坝，在供水、防洪、发电等多个方面，发挥着重大的作用。但是，在水利大坝建设过程中，水库具有涉及范围广泛、淹没面积大等特点，为周围居民带来极大的不利影响，如房屋倒塌、耕地淹没等，产生了大量的水库移民[1]。如何妥当安置水库移民，是现今水利水电行业亟待解决的问题之一，并关系着水利枢纽工程的成败与效益。

水库移民实质上是一种具有强迫性质的非自愿行为，此种行为会彻底改变居民的生产与生活方式，对其造成颠覆性的改变。水库移民安置是一项复杂系统工程，受多种因素的影响，如经济条件、环境条件、社会条件等。水库移民安置需要以人为出发点，结合环境、资源与可持续发展战略，依据实际情况制定相应的水库移民安置方案。在水库移民安置过程中，最关键的环节就是安置区的选择规划，其是移民以后生活条件与发展潜力的决定因素。只有充分考量多方面因素(社会环境、自然资源、区位条件、生产用地条件、基础设施条件等)，合理选择规划水库移民安置区，才能实现国家制定的“搬得出，稳得住，能致富”的移民安置目标。已有方法由于考虑因素较少，无法获得最佳安置区选择规划效果，制约了水利水电行业的发展步伐。因此，本文提出基于粗糙数据集的水库移民安置区选择规划方法进行研究。

1 水库移民安置区选择规划方法研究

1.1 水库移民安置区类型划分

水库建设位置主要为农村区域，则水库移民的主体对象为农民[2]。就现有情况来看，水库移民安置区类型为本村后靠安置区、出村本乡近迁安置区及出乡外迁安置区，示意图见图1。

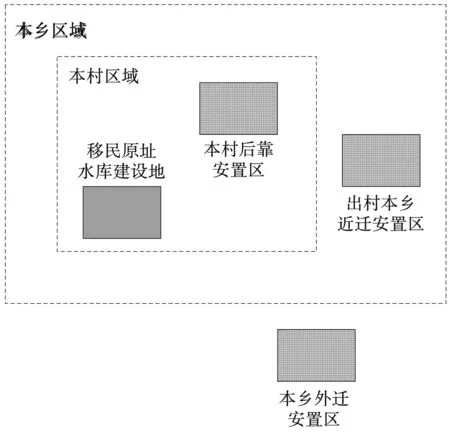
图1 水库移民安置区类型示意图

其中，本村后靠安置区是指在原区域附近选择适合的区域作为安置区。由于搬迁距离不远，已有基础设施仍然可以应用，能够降低移民安置的资金投入，简化移民安置工作。从水库移民角度出发，既能够满足乡土情感，也容易适应新的生产与生活环境。水库蓄水后淹没的耕地往往是条件较好、经济效益较高的田地，说明水库建设后，本村后靠安置区的剩余环境容量极其有限,若是移民数量过多，会导致安置区人口密度过大，人地矛盾突出，从而破坏生态环境，也会影响安置区的经济发展。由此可见，虽然本村后靠安置区是首选安置方式，但是在安置规划时，需要将环境承载能力考虑在内，防止生态破坏事件的发生[3]。

出村本乡近迁安置区是指在本乡范围内、原村范围外选取适合的区域作为安置区。相较于本村后靠安置区，出村本乡近迁安置区距离原址距离更远，环境容量较为富余，能够为移民提供充足的发展空间。但与此同时，由于搬迁较远，移民需要适应新的生产与生活方式，会造成安置区社会稳定性较差，需要对此方面进行关注与介入管理[4]。

出乡外迁安置区是指在本乡范围外选取适合的区域作为安置区。此种安置方式距离原址最远，选址范围较大，但是生产与生活方式差距也较大，需要移民重新适应，学习新的生产技能等，才能逐渐实现安置区的稳定发展。因此，在水库移民安置过程中，需要将移民适应性与自身意愿考虑在内，防止移民返迁事件的发生。

通过上述过程，完成了水库移民安置区类型的划分与深入分析，为后续安置区选择指标体系构建提供充足的准备。

1.2 安置区选择指标体系构建

以上述划分的水库移民安置区类型为基础，依据全面性原则、可操作性原则、层次性原则、系统性原则对安置区选择指标进行选取，构建选择指标体系，为移民安置区选择打下坚实的基础[5]。

水库移民安置区选择指标体系见表1。

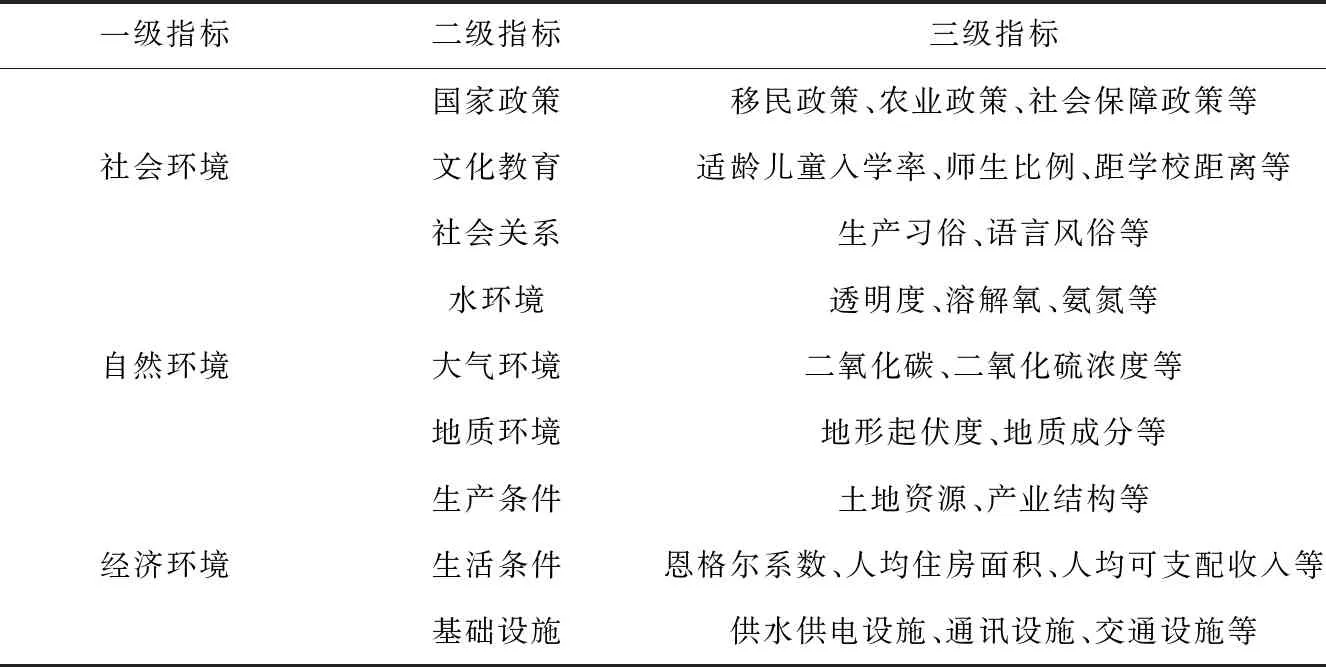
表1 安置区选择指标体系表

由表1可知，构建的安置区选择指标体系中包含3个一级指标，9个二级指标及其若干个三级指标。由于篇幅的限制，只在表1中展示部分三级指标。上述指标能够显示安置区的全部环境信息，为后续安置区的最优选择提供支撑。

1.3 水库移民安置区选择决策

以构建的水库移民安置区选择指标体系为依据，获取相应的指标数据，基于粗糙数据集理论构造粗糙数，计算安置区选择指标的权重数值，生成安置区选取决策矩阵，获得水库移民安置区选择的最终决策[6]。

已有方法主要通过专家打分方法确定指标权重，极容易受到主观偏好的影响，造成权重误差较大，安置区选择决策结果不是最佳的。而粗糙数无需任何先验知识，完全依靠原始数据对个体认知进行有效的整合，获得群体偏好，权重数值计算更加准确，为安置区选择提供更加精确的数据依据[7]。故此研究基于获取的指标数据与粗糙数据集理论构造粗糙数，具体如下：

设定安置区选择决策数据系统为R={C1,C2,…,CN}，其中N代表论域中数据总数量。若n个数据之间存在有序关系，依据数据Ci的上近似集与下近似集，即可获得数据Ci对应粗糙数的上限与下限，表达式为：

(1)

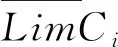
依据式(1)计算结果，即可将安置区选择决策数据转换成粗糙数形式，表达式为：

(2)

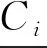
依据式(2)将安置区选择决策数据全部转换为粗糙数形式，但由于安置区范围较大，类型较多，粗糙数据集规模较大，使得安置区选择效率降低，不利于水利工程的实施，故对粗糙数据集进行约简处理，以此来删除重要度较低的指标数据，降低粗糙数据集的维度，减少安置区选择决策运算量[8]。

粗糙数据集约简流程见图2。

图2 粗糙数据集约简流程示意图

图2中，T代表重要度标准阈值，需要根据安置区的实际情况进行制定，以此来获得最佳的粗糙数据集约简结果[9]。

以约简后的粗糙数据集为基础，结合最优最劣法对权重数值进行计算，具体步骤如下：

步骤一：设置最优指标与最劣指标，分别记为CB与CW。

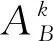
(3)

式中：n为安置区选择指标数量；k的取值范围为[1,s]，s代表打分专家的人数[10]。

另外，对全部判断向量进行一致性检验。若是不满足一致性条件，需要对判断向量进行一定程度的调整，直到全部判断向量均具有一致性后，才能对判断向量进行应用、分析与计算[11]。

步骤三：整合处理全部判断向量，获得整合比较向量，记为AB与AW。

步骤四：集结群体信息，并结合步骤三获取的比较向量，构造粗糙比较向量[12]。整合比较向量中元素粗糙数表达式为：

(5)

步骤五：利用数学规划对每个安置区选择指标粗糙权重数值进行求解[13]。安置区选择指标粗糙权重表示为：

(6)

式中：ωB与ωW分别为最优指标与最劣指标对应的粗糙权重；ωj为第j个安置区选择指标粗糙权重数值。

1.4 水库移民安置区规划

以上述水库移民安置区选择决策结果为依据，结合安置区的实际环境情况以及移民诉求，对安置区进行适当的规划，为移民后续生产与生活提供支撑。

一般情况下，安置区人均用地控制在70 m2左右，学校用地控制在25 m2左右，实际建设时，需要根据安置区的情况进行适当的面积调整[15]。另外，用电标准设置为每人150 W，用水标准设置为每人每天90 L。主道路宽度约为6 m，住宅前方道路宽度约为2.5 m。由于篇幅的限制，不对规划内容进行详细的赘述。

通过上述过程完成了水库移民安置区的选择规划。基于粗糙数据集理论计算了安置区选择指标权重数值，能够增加权重计算的客观性，获得最佳的选择结果，为水库移民提供更好的环境空间，并推动水利工程的顺利进行。

2 实验与结果分析

为了验证提出方法的应用性能，选取基于模糊理论的李家河水库农村移民安置区优选[16]作为对比方法，设计对比实验，具体实验过程如下。

2.1 实验准备

选取某水利大坝建设工程作为实验背景，为了方便实验的进行，将水库建设位置与可选择安置区位置关系进行简化展示，具体见图3。

图3 水库位置与可选择安置区位置关系示意图

由图3可知，水库建设位置是固定的，而可选择的安置区位置共有8个，每个安置区的环境容量均是不同的，需要依据水库移民的数量与诉求对安置区进行相应的选择决策。

获取可选择安置区相关信息，为后续实验进行提供便利，具体见表2。

表2 可选择安置区相关信息表

另外，由于水库移民安置距离相对来说较近，为了简化实验过程，设置可选择安置区的生产与生活习俗是相同的，不需要移民进行重新的适应与学习。

2.2 实验结果分析

以上述实验准备内容为基础，进行水库移民安置区选择规划实验，通过移民安置区选择时间与安置区规划评估参数显示提出方法的应用性能，具体实验结果分析过程如下：

其中，水库移民安置区选择时间计算公式为：

(7)

式中：t为水库移民安置区选择时间；TE与TS分别为水库移民安置项目的结束时间与开始时间；α*为安置区选择时间计算辅助参数，取值范围为[1,10]。

通过实验获得水库移民安置区选择时间数据见图4。

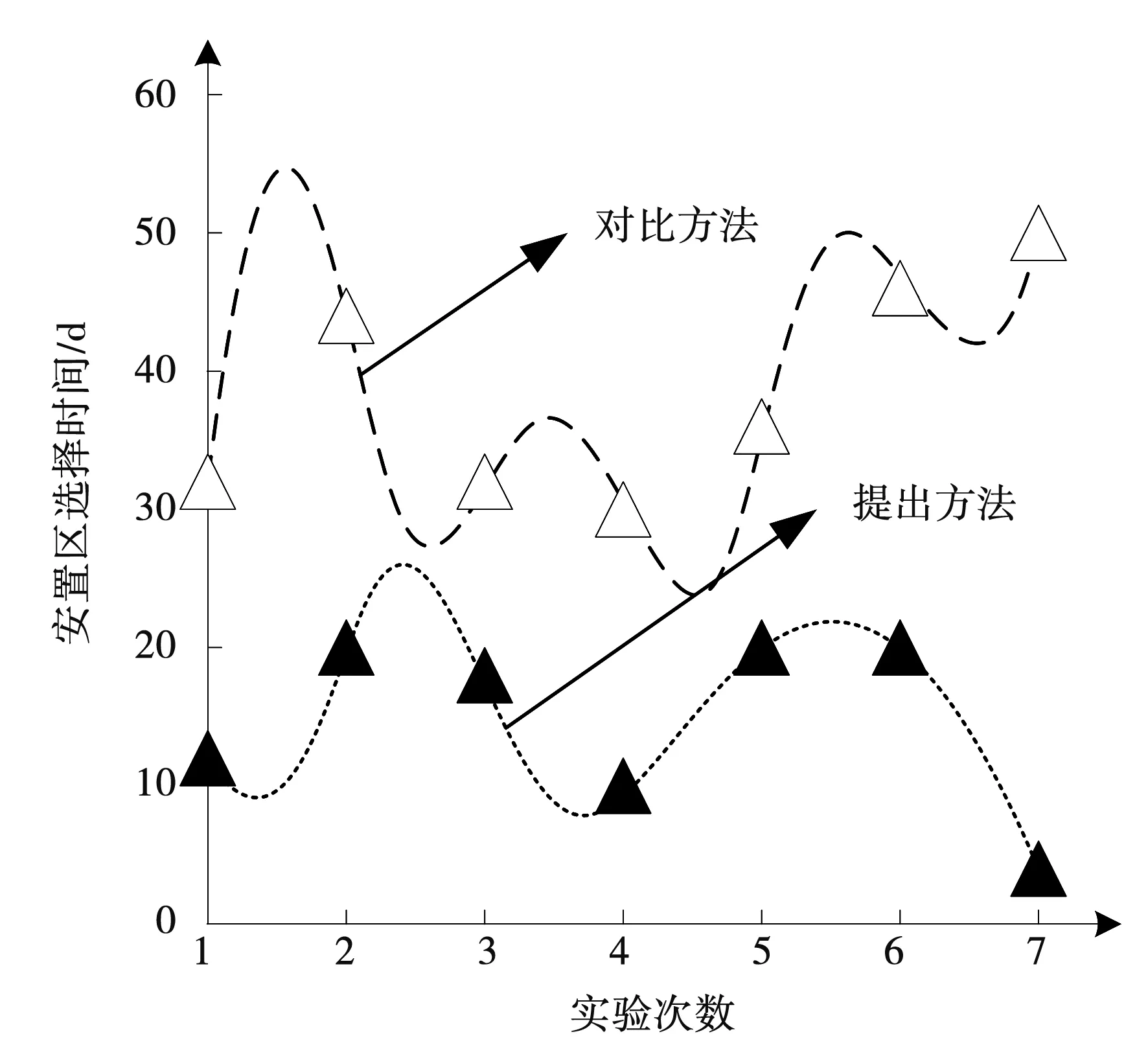
图4 水库移民安置区选择时间数据图

由图4可知，与对比方法相比较，应用提出方法获得的水库移民安置区选择时间更短，说明提出方法的效率更高。

水库移民安置区规划评估参数主要是借鉴已有文献研究成果，其计算公式为：

(8)

式中：ξ为水库移民安置区规划评估参数；xi为安置区规划效果评估指标；ωi为安置区规划效果评估指标对应的权重数值；β与ϑ为安置区规划评估参数计算常数。

根据已有文献可知，水库移民安置区规划评估参数越大，表明安置区规划效果越好；反之，水库移民安置区规划评估参数越小，表明安置区规划效果越差。

通过实验获得水库移民安置区规划评估参数见图5。

图5 水库移民安置区规划评估参数示意图

由图5数据可知，与对比方法相比较，应用提出方法获得的水库移民安置区规划评估参数更大，表明安置区规划效果越好。

上述实验数据表明，相较于对比方法，提出方法获得的水库移民安置区选择时间更短，安置区规划评估参数更大，充分证实了提出方法具有较好的安置区选择规划效果。

3 结 语

此研究基于粗糙数据集理论设计了新的水库移民安置区选择规划方法，并通过实验验证了提出方法的有效性与可行性，极大地缩短了水库移民安置区选择时间，提升了安置区规划评估参数，为水库移民安置提供了更加有效的方法支撑，也为安置区选择规划研究提供一定的参考。