计及源荷双侧不确定性的综合能源系统优化配置

陈美玲，高 岩

（上海理工大学 管理学院，上海 200093）

随着经济社会的不断发展，环境、能源等问题备受关注，风电、光伏等新能源发展迅猛。由于风光等清洁能源出力的波动性与间歇性，将其并网会使得系统的稳定性有所下降，因此，解决能源出力不确定性问题是风、光等清洁能源并网需解决的关键问题[1-3]。对于风光负荷的不确定性，文献[4-5]采用预测值加上预测误差表示风、光及负荷的实际值，先假定预测误差均服从正态分布，再采用机会约束的方法处理源荷双侧不确定性，在一定的置信水平下通过正态分布函数的概率密度函数将不确定性问题转化为确定性问题[6]进行求解，再考虑风电出力不确定性场景下建立综合能源系统。

综合能源系统(integrated energy system,IES)可以有效提高能源利用率，缓解世界能源短缺，减少环境污染，降低系统成本[7-12]。为了提高综合能源系统的利用效率，仅仅依靠供给侧是不够的，需进行需求侧管理[13]，需求响应是需求侧管理的重要手段之一。在电力市场中需求响应(demand response,DR)主要分为激励型需求响应和价格型需求响应(price-based demand response,PBDR)[14-15]。其中，价格型需求响应最典型的是实时定价和分时定价[16-20]。文献[21-22]主要讨论了用户的用电行为和用户对不同电价的敏感性。文献[23]先通过模糊聚类方法根据电荷划分峰谷，研究了分时电价削峰填谷的作用，但未考虑综合能源系统。文献[9]考虑了综合能源系统并采用 Cplex 求解最低运行成本。文献[24-25]主要研究了需求响应在综合能源系统中带来的经济和环境效益，IES 提高了能源的利用率[26]，但未考虑清洁能源。文献[27]在研究分时电价时主要考虑了风电，未考虑光伏与天然气等清洁能源。由于源荷双侧不确定性[28-29]是影响经济性和可靠性的重要因素之一，同时考虑源荷双侧不确定性下进行综合能源系统的优化配置是需要研究的重要问题。

上述研究中较少有文章结合需求响应，同时考虑风光等清洁能源，从分时电价的角度出发对综合能源系统的配置进行优化。本文在考虑风光出力不确定性的基础上，建立电热气耦合的综合能源系统，同时将需求响应下的分时电价模型应用于综合能源系统，进行系统的优化配置。文章目标函数的总成本不是简单采用二次函数进行计算，而是通过等额投资成本、运行成本、燃料成本等各分项成本加总求得，更方便进行不同场景下成本的比较分析，具有一定的现实意义。通过算例分析证明 PBDR 策略可以减少高峰期的负荷需求，并将高峰时期的负荷转移到其他时间段，从而使低谷时期需求增加，起到削峰填谷的作用。并且不同场景下设备的容量配置、设备出力及发电成本也有差异，只考虑PBDR 的场景时运行成本明显较低，考虑风电出力不确定性及PBDR将会优于只考虑出力不确定性。

1 综合能源系统基本结构

本文选用综合能源系统结构，主要考虑用户的电热气负荷，所以在构建的IES 中以风机(wind turbine,WT)、光伏 (photovoltaic,PV)、热电联产设备(combined heating and power,CHP)、电转热设备电锅炉(electrical boiler,EB)、气转热设备燃气锅炉(gas boiler,GB)、蓄电池（battery discharge,BD）及储热（heat storage，HS）设备等[30]为主要研究对象进行优化配置。综合能源系统的基本结构如图1所示。

2 综合能源系统建模

2.1 源荷不确定性模型

在已知风速的情况下，可以根据以下分段函数得到风速与风电功率之间的关系[28]：

式中：vin和vout分 别表示切入风速和切出风速；vrated表示额定风速；vt表 示实时风速；PR表示风机的额定功率。同时，光伏出力[28]如下

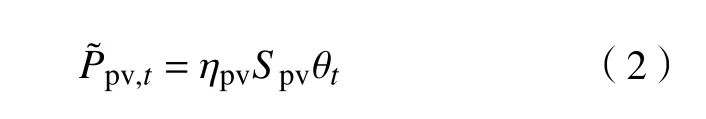
式中：ηpv为太阳能辐射效率；Spv为太阳能辐射面积；θt为t时刻的光照强度[30]。

由于风光等清洁能源受天气等客观因素的影响较大，故发电出力的波动性较大，为了尽量避免出力不足的后果，考虑风光出力有一定的预测误差，风光出力及负荷的实际值为[29]

式中：σt表示t时刻预测误差的标准差；ρt表示t时段风光负荷预测偏差占预测值的百分比[29]。

2.2 需求响应模型

需求响应是实现需求侧管理的有效手段之一。分时电价作为价格需求响应的一种，主要是通过调整电价，影响电价敏感型用户的用电行为，起到平缓负荷需求曲线的作用。在用电过程中，通常可以用价格弹性系数表示用户用电量对于价格的反应程度，表达式为

式中：Lc0和Pc0分别表示该用户需求响应前的负荷和价格；ΔLc和 ΔPc分别表示需求响应的价格变动量和负荷变动量；s和t表示时刻从1 变化到T（T=24），当s=t时表示自弹性，当s≠t时表示交叉价格弹性；c表示用户。需求响应后的负荷[27]为

式中：Lc表示需求响应后的负荷；E表示价格弹性系数矩阵，见表1。

表1 用户弹性系数Tab.1 Elasticity coefficient of users

峰谷时段的划分与分时电价的实施效果直接相关。由初始给定的负荷需求划分用电的峰平谷时段，再给定峰平谷时段的电价，最后进行系统优化建模求解。根据所构建的综合能源系统采用模糊聚类方法[23]划分峰平谷时段。首先对各时段的负荷数据与最大最小值点进行隶属度的计算，然后对数据进行标定得到模糊矩，再采用传递闭包法求得模糊相似矩，最后进行适当的聚类得到峰平谷时段的划分。

a.首先找出每个负荷的最大与最小值点，再通过计算各时点负荷数据与最大最小值点间的距离对各时点负荷数据进行相应的标准化处理。

式中：Qx表示某时段的用户用电量；Qmin和Qmax分别表示所有时段的最小和最大用电量；Sx1和Sx2分 别表示第x时段Qx与Qmin和Qmax的距离。

b.利用计算所得的隶属度，根据欧几里得距离法进行标定得到模糊相似矩R。

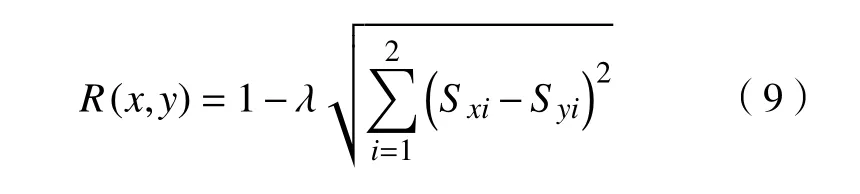
式中：下标x，y分别表示第x段、第y段；λ 表示一个常数系数，使得模糊矩的各元素都在0～1 之间；R(x,y) 表示R中第x行，第y列的元素。

c.得到的相似矩可能不具有传递性，所以利用传递闭包法求得模糊相似矩的等价矩阵R′，其中表示R′中第i行、第j列的元素，再对R′进行判定，设定工业用户和居民用户的系数 μ 分别为0.60 和0.55。

d.通过对R′中元素进行判定得到新的矩阵M，再对矩阵M中的行元素进行求和，将相同的行元素之和划分为同一个时段，一般来说一天的电价可以划分为峰平谷3 个时段。

3 综合能源系统优化模型

选用综合能源系统结构，在考虑源荷双侧不确定性的条件下，通过对不同场景对比分析研究电热气耦合系统中分时电价削峰填谷的作用，主要考虑工业用户和居民用户的应用场景。以所构建的 IES 为基础，以总成本最小为目标，同时考虑平衡约束、运行约束、储能约束、旋转备用约束进行系统的优化配置。

3.1 目标函数

综合能源系统中优化配置的总成本主要涉及固定投资和运行这两部分，其中运行部分的成本主要包括运行维护、燃料消耗以及环境成本，则年总成本为

式中：Cinv表示年等额投资成本；Cope表示运行成本；Cfuel表示燃料成本；Cen表示环境成本。

年等额投资成本为[29]

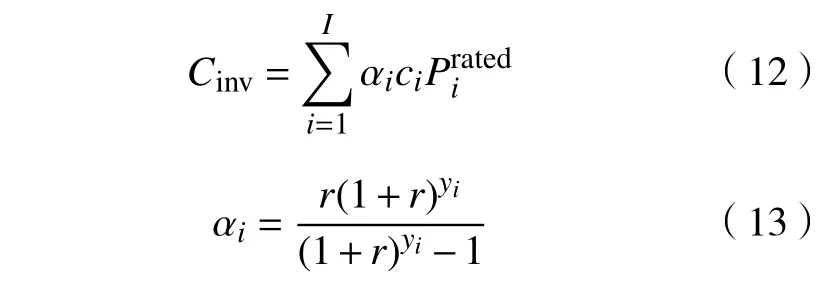
式中：αi表示设备i的年等额投资折算系数；ci表示设备i的单位投资成本；表示设备i的额定功率；r表示年利率；yi为设备i的生命周期。

设备运行阶段的成本包括燃料成本、运行成本、环境成本。运行成本又包括固定运行维护成本和可变运行维护成本[29]，即

式中：vi表示设备i的可变维护成本；fi表示设备i的固定维护成本系数；表示设备i在第d天t时刻的输出功率。

燃料成本[31]可通过式（15）计算

式中：ψj，λj，υj分别表示单位煤耗的污染物排放量、环境价值及惩罚成本[29]；Coal表示消耗的年标准煤总量；m为污染物的种类。

环境成本与耗煤量之间的关系[30]为

式中：μj表示第j种能源的标准煤转化系数[30]；表示第j种能源在第d天t时刻的消耗量。

3.2 约束条件

为了保证系统规划的合理性以及建立模型的可行性，优化模型中主要有能源功率平衡约束、能源转化的设备运行约束、能源存储的设备约束、能源的备用约束。

a.能源功率平衡约束。

d.能源的备用约束。

为保证综合能源系统的运行不受风光出力不确定性的影响，在同时考虑源荷双侧不确定性的情况下，发电机组需要考虑到旋转备用约束[4]：

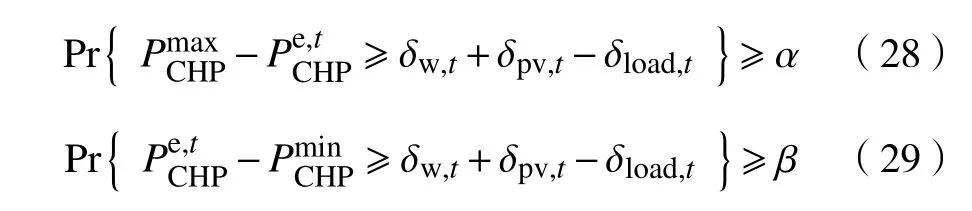
在一定的置信水平下采用机会约束的方法将上述不确定性问题转化为确定性[4]问题

式中：φ (·) 表示标准正态分布；α，β 表示置信水平，本文均取90%。

3.3 模型生成和求解

计及风光不确定性的综合能源系统优化配置模型为0-1 混合整数非线性(NLP)规划模型，标准模型形式[9]如下

式中：F(x) 为 目标函数，这里为总成本；gi(x) 和hi(x)表示等式约束和不等式约束，分别对应功率平衡约束和设备运行时的功率约束。

分时电价主要通过影响电功率平衡优化配置，而源荷双侧不确定性是通过正态分布的概率密度函数转化为确定性放入备用约束中，再代入设备运行时的功率约束hi(x) 中进行求解，m，n为对应的等式约束和不等式约束的个数。xmin和xmax为变量xj的上下界，文中为设备运行功率的上下界，u为状态变量。

非线性规划模型的求解常采用 LINGO、CPLEX、GAMS 进行求解。本文将模型先转化为混合整数非线性规划问题，再在 Matlab 环境下，采用Yalmip建模并调用 Cplex 求解器进行求解，流程如图2 所示，具体步骤如下：

图2 IES 优化流程Fig.2 Optimization process of IES

步骤1输入设备参数及负荷数据；

步骤2定义决策变量；

步骤3输入等式约束及不等式约束；

步骤4构造总成本最小的目标函数；

步骤5求解优化变量及目标函数并记录最终输出值；

步骤6判定此时的解是否为最优解，若是则输出结果，若不是，则返回步骤5，直至找到最优解。

4 算例分析

4.1 算例介绍

本文从分时电价的角度对工业用户和居民用户的负荷需求进行分析。IES 主要由1 个1.5 MW的风电场、1 个1 MW 的光伏电站以及 CHP、GB、EB、储电与储热设备[30-31]构成。切入风速为3 m/s[28]、额定风速为14 m/s[28]、切出风速为25 m/s[28]。太阳辐射效率为85%、光伏面积为1 600 m2。风光及负荷的预测误差分别为15%[29]，8%[29]，1%[4]。风光出力预测曲线如图3 所示。

图3 风光出力曲线Fig.3 Outputs curve of PV and WT

设定从配电网购电价格为0.4 元/(kW·h)、售电价格为其75%，购气价格为0.35 元/(kW·h)，用户侧的固定电价为0.5 元/(kW·h)。每小时最大买卖电量为3 000 kW，且买卖电量不同时进行，每小时最大购气量为5 000 kW，储能设备的额定容量为300～3 000 kW·h。图4 为初始的用户负荷需求。

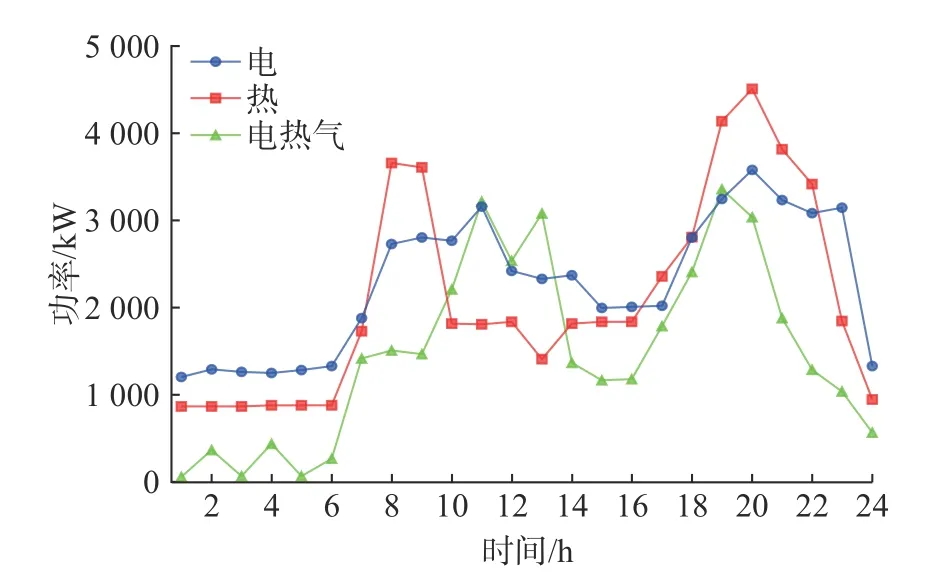
图4 用户日负荷需求曲线Fig.4 User's daily load demand curve

文中的场景可以分为4 种情况，如表2 所示。

表2 场景分类Tab.2 Scenario classification

其中，考虑机会约束的置信水平为90%，未单独列明的均为综合场景下的优化结果，以场景1 为基本场景进行对比分析。

场景1：不考虑机会约束和 PBDR；

场景2：只考虑机会约束；

场景3：只考虑 PBDR；

场景4：同时考虑机会约束和 PBDR。

4.2 算例结果分析

首先通过模糊聚类方法，分别对工业用户和居民用户进行用电时段的划分，得到工业用户的峰时段为8:00—11:00 和18:00—23:00，平时段为7:00 和12:00—17:00，谷时段为24:00—6:00。居民用户的峰时段为11:00—14:00 和19:00—23:00，平时段为7:00—10:00 和15:00—18:00，谷时段为24:00—6:00。峰时段电价为固定电价的1.2 倍，谷时段电价为固定电价的0.8 倍，平时段电价保持0.5 元/(kW·h)不变。

在峰平谷时段划分的基础上，进行需求响应后负荷用量的求解。由图5 可知，PBDR 可以削减峰时段的负荷用量，同时激励谷时段的负荷需求，起到削峰填谷的作用，表明相比于固定电价，分时电价会引导用户合理化一定时段内的用电量，从而减少负荷总需求。工业用户在实施峰谷分时电价前后的负荷需求量变动较大，对电价较敏感，响应程度较大，相比之下，居民的负荷曲线变动较小。

图5 PBDR 前后的负荷需求曲线Fig.5 Load demand curve before and after PBDR

对于用户侧而言可以合理化用电时段以提升自身的效用值，但对于综合能源系统而言，总是追求最小成本以达到最大利润。表3 对4 种不同场景下的总成本及各分项成本进行相应的比较，其中，单位发电成本为总成本与总负荷需求量的比值。

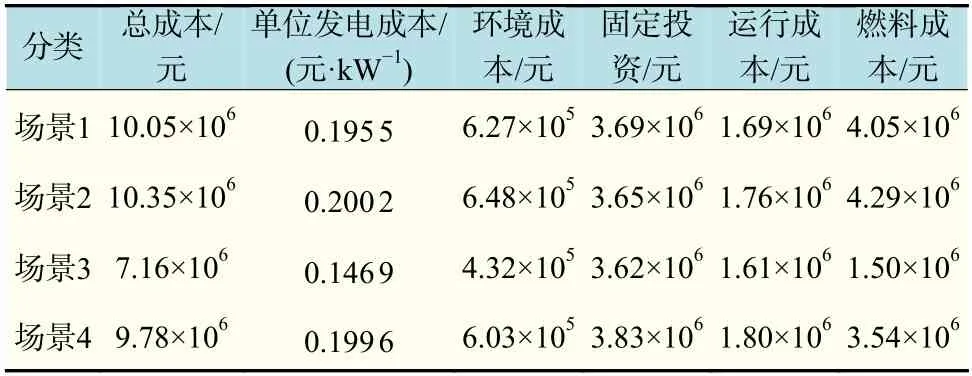
表3 不同场景下的成本Tab.3 Cost of different scenarios

场景1 为不考虑不确定性和PBDR 的基本场景，场景2 则考虑风光出力不确定性。对比场景2 和场景1 可知，在考虑风光出力不确定的情况下系统的总成本、各分项成本以及单位发电成本均有所增加。

场景3 与场景1 相比，燃料成本和环境成本下降显著，表明分时电价的实施有效引导用户更为合理的用电，减少燃料消耗，同时也减轻了污染，降低了总成本及单位发电成本。

场景4 同时考虑不确定性和PBDR，与只考虑风光出力不确定性的场景2 相比，总成本和单位发电成本均有所降低。但与只考虑PBDR 的场景3相比，场景4 的总成本和单位发电成本均增加，表明考虑风光不确定性会增加系统的单位发电成本，但PBDR 会削减部分单位发电成本，所以总的来看单位发电成本较场景1 是降低的。并且不同场景下的设备容量配置也有所不同，这也是各场景下成本不同的重要原因，设备的容量配置优化结果如表4 所示。

表4 优化配置的结果Tab.4 Results of optimized configuration kW

表4 中，燃气锅炉的配置均为0，可能是热电联产设备 CHP 及电锅炉的优化配置足以提供热负荷需求。表3 的固定投资成本与优化配置容量有关，场景4 为综合考虑风光出力不确定性和PBDR，它的容量配置最高，固定投资成本较高，但其燃料成本和环境成本减少而使得总成本较场景1 和场景2 下低。场景3 在只考虑PBDR 的情况下，电锅炉 (EB) 和储热箱 (HS) 的容量配置都减小，可能是用户用电量减少，电负荷需求减少，并且电锅炉可以将电能转化为热能，从而降低储热箱的配置。

根据电功率平衡等式可以得出设备的优化出力结果，其中输出电功率设为正值，消耗电功率设为负值，需求响应前后设备的电功率如图6 和图7 所示。

图6 场景1 电能供需平衡图Fig.6 Electric load balance of scenario 1

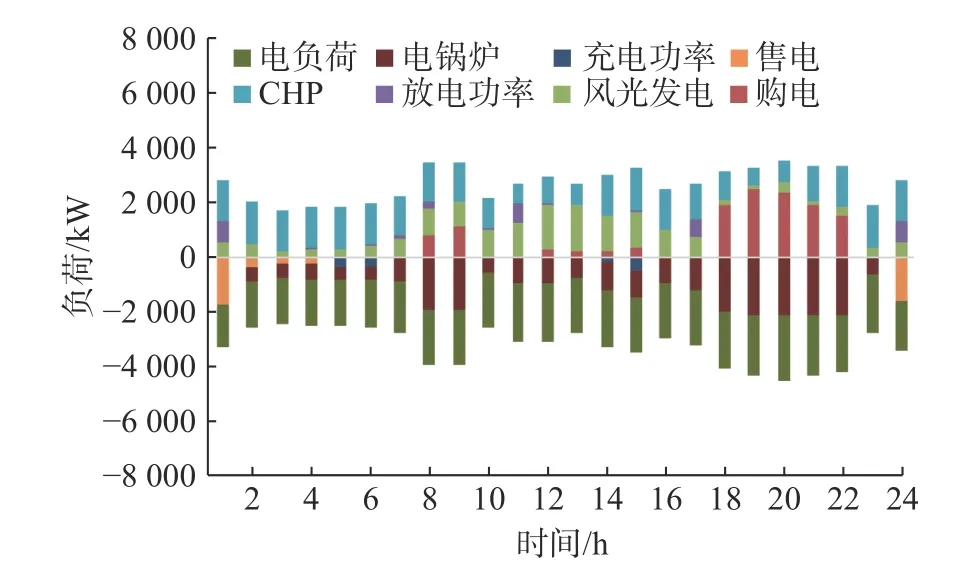
图7 场景3 电能供需平衡图Fig.7 Electric load balance of scenario 3

图6 柱状图的高度差比图7 明显，其中8:00和20:00 是电负荷消耗较多的时刻，PBDR 的实施减少了电能的使用，电锅炉的配置变化较小，但储热箱的配置变化较大，可能是电热气耦合的综合能源系统使得部分电能转化为热能。

5 结 论

文章同时考虑源荷双侧不确定的情况下，以最小化成本为目标制定分时电价的研究策略，对不同场景下的综合能源系统进行优化配置并对比分析，最后实例仿真结果验证了所提模型的有效性，得出以下结论：

a.考虑风光等清洁能源并网场景下，会增加系统出力的不确定性，使得运行成本、燃料成本以及总成本增加，从而使得单位发电成本增加。

b.利用需求侧峰谷分时电价的方法，更有利于电热气耦合网络中能源之间的相互转化与协调，调整及降低设备的容量配置，提高综合能源系统的经济运行效率，降低运行成本及单位发电成本。

c.在综合考虑不确定性和需求响应的情况下，虽然设备的容量配置较高，但其系统较稳定，所以其总成本也有所降低。

未来可以扩展情景分析，例如加入相关对比分析，不局限于固定电价和分时电价，可进一步讨论实时电价和尖峰电价。