基于双目视觉的无人机编队相对定位算法

周文雅，李 哲，许 勇，杨 峰，贾 涛

(1.大连理工大学航空航天学院，大连 116024；2.中国空气动力研发中心空天技术研究所，绵阳 621000)

0 引 言

无人机具有操作灵活、生产成本低和无人员伤亡等优点，广泛应用于军事和民用等领域。由于单个无人机能完成的任务量有限，往往需要多个无人机组成编队，协同完成侦查、作战及目标跟踪等任务。为实现无人机编队飞行，必须首先解决编队无人机间相对定位问题。

传统的目标定位技术主要利用雷达、激光等传感器，这些传感器容易受到无人机上其它传感器的干扰，导致定位不准确，此外，这些传感器也无法识别具体的目标物体。近年来，随着计算机视觉技术的发展，利用视觉进行目标定位的方法成为目前新兴的一种定位方法。视觉传感器所需的实验环境和硬件条件更加宽松,生产成本低，具有信息量大、检测范围大等特点。因此研究基于视觉的目标定位技术具有重要意义。

视觉定位的前提是检测目标在视觉图像中的位置，目前常用的目标检测方法有特征点法和机器学习。特征点法与机器学习相比，具有优势：1)检测通用性，机器学习事先需采集大量目标图片作为训练样本，特征点法则不限制目标的具体类型;2)检测精确性，机器学习识别目标的大致区域，特征点法能够在像素级别上检测目标，进而也能提高目标定位的精确性。对于特征点算法，文献[10]提出了一种尺度不变特征变换(Scale-invariant feature transform，SIFT)算法，其检测的特征点对图像的尺度和旋转能够保持不变，即尺度不变性和旋转不变性，对噪声及视角变化具有较好的鲁棒性，但该算法采用图像金字塔，使得图像尺度较多，且特征点描述向量的维数较高，导致算法计算量较大，实时性不高；文献[11]提出了一种加速鲁棒性特征(Speeded up robust features，SURF)算法，SURF算法是SIFT算法的改进版本，保持了尺度不变性和旋转不变性的同时，增强了算法的鲁棒性，且计算速度提升了至少三倍，但计算量仍然较大；文献[12]提出了ORB算法，ORB算法的运行速度相比于SURF算法和SIFT算法要快很多，只具有旋转不变性，没有尺度不变性。但对于双目视觉，双目图像间没有尺度变化，所以ORB算法仍能很好地应用于双目视觉的特征点匹配，并保证匹配精度。

视觉定位依据视觉传感器的数量可分为单目视觉定位和双目视觉定位。单目视觉无法直接获得视场的深度信息。双目视觉能够利用双目间的旋转和平移参数，解算深度信息，进而获得目标的三维位置。文献[16-17]通过机器学习的方式识别图像中的人类、工件目标，再通过双目视觉定位目标位置，由于人类、工件目标较小且形状规则，容易确定目标中心，使定位误差较小，但对于形状不规则的较大无人机目标，通过双目识别方式确定的目标几何中心实际未必是精确对应的，进而导致定位的无人机位置有较大误差。文献[18]提出了一种基于改进SIFT算法的双目定位算法，通过减少SIFT算法中尺度空间的数量，降低了特征点描述向量的维数，进而降低了SIFT算法的复杂度，在提高计算效率的同时也造成了精确度的损失。文献[19]使用背景差分技术确定目标在图像中的感兴趣区域，在该区域内使用SURF算法进行特征点提取与匹配，再利用双目视差对特征点进行定位。由于只在感兴趣区域内进行特征点提取与匹配，提高了SURF算法的计算效率，进而提高了双目定位效率。文献[20]利用Zynq SoC高速处理器对SURF算法进行硬件加速，以实现双目图像的特征快速匹配，从而达到实时定位效果，但增加了无人机的生产成本。文献[21]基于ORB算法对双目图像进行特征点匹配，并利用双目实现了特征点的深度估计，但ORB算法容易受到背景环境干扰，提取的特征点不是全部集中在目标物体上。文献[22-23]通过计算特征点的视差实现特征点定位，但基于视差原理的定位算法要求双目图像是平行且行对准的，这就要求双目视觉设备具有较高的制作工艺。文献[24]使用Bouguet的校准算法实现了左右双目图像共面且行对准，并基于视差原理计算得到目标的三维位置信息。文献[26]利用特征点的对极约束条件提高了特征点的匹配精度和定位精度。

针对无人机编队飞行时双目视觉定位的精确性和实时性要求，本文对ORB算法进行了改进，提高了算法的计算效率，也提高了特征点匹配的精确度；双目视觉定位模型更符合实际情况，避免了要求双目平行且行对准的严格限制条件；将改进ORB算法提取的无人机特征点代入到双目视觉定位模型中，实现了无人机的三维定位；进一步利用卡尔曼滤波算法对无人机的三维定位信息进行估计，提高了定位精度。实验表明，基于特征点的无人机视觉定位算法满足无人机定位的精确性和实时性要求，具有工程应用价值。

1 ORB算法及改进

1.1 传统ORB算法

ORB算法包括三部分内容：特征点提取、特征点描述和特征点匹配。ORB算法由加速段测试特征(Features from accelerated segment test，FAST)提取算法和二进制鲁棒独立基本特征(Binary robust independent elementary features，BRIEF)描述算法组合并改进而成，这两者具有很快的运算效率，但都不具备旋转不变性和尺度不变性。ORB算法在这二者的基础上，通过定义特征点的方向角度，实现了旋转不变性。

ORB算法对特征点进行提取与描述后，用描述向量的距离表示两个特征点之间的相似程度。测量左目图像中的特征点与右目图像中所有特征点的距离，并取距离最近的一对特征点作为匹配点。由于BRIEF特征点描述算法采用二进制字符串的描述形式，所以使用汉明距离作为两个特征点相似程度的度量。

1.2 ORB算法改进

利用双目视觉确定无人机编队中无人机间的相对位置时，发现以下问题：一是受双目图像中无人机的背景环境的干扰，使用传统的ORB算法进行双目图像间的特征点匹配时，存在许多错误匹配的特征点对，影响了特征点匹配的精确性；二是双目图像中存在非目标区域，而ORB算法中关于特征点的操作是基于整幅图像的，致使算法中存在对非目标区域的无意义计算，影响了算法的计算量和实时性。针对以上问题，本文对ORB算法做出了如下改进：

1)目标区域提取

通过目标区域提取，确定了无人机在图像中的位置区域，可以减少不相关区域的特征点检测与匹配，同时避免目标背景对特征点提取与匹配的干扰。本文确定无人机目标区域的方法是利用边缘检测技术描绘图像中无人机的边缘曲线，以边缘曲线包含的区域代表无人机的位置区域，处理流程如图1所示。对应的具体处理步骤如下：

(1)对双目图像进行灰度化处理，以增强图像各点邻域强度的变化值，也能减少边缘检测时的计算量；

(2)对灰度图像进行高斯滤波处理，防止将图像中的噪声识别为边缘；

(3)对滤波后的图像进行边缘检测；

(4)对边缘检测图像进行膨胀处理，以突出目标的边缘曲线；

(5)对膨胀后的图像进行闭运算操作，消除边缘曲线邻域内的小型斑块；

(6)识别图1(d)中白色区域的最外边界轮廓，并返回能包围轮廓的最小矩形位置信息，即矩形的四个角点的像素坐标信息；

(7)以计算的矩形位置区域作为目标无人机的区域，将矩形显示在原始图像上，如图1(e)所示。

图1 目标提取流程

2)最近邻约束

采用快速近似最近邻搜索包(Fast library for approximate nearest neighbors，FLANN)对特征点进行匹配，FLANN适用于特征点数量较多和特征描述向量维度较高的情况。对于左目中的一个特征点，FLANN从右目中找到汉明距离最近的前两个关键点，如果最近的距离除以次近距离的比值少于某个阈值，则可确定左目特征点与右目中距离最近的特征点是一对匹配良好的特征点。对于阈值参数的选择，本文设置为0.5。若设置阈值过小，则双目匹配的特征点过少；若设置阈值过大，则存在大量错误匹配点。

3)RANSAC方法剔除误匹配点

对于通过最近邻约束筛选的特征点匹配集合，还可能存在特征点交叉错误匹配的现象。RANSAC方法通过对样本进行随机抽样，以估计模型参数，进而识别样本中的外点，最后以迭代方式估计模型的最优参数。具体步骤为：

(1)在通过最近邻约束筛选的特征点匹配集合中，随机选取八个特征点对，计算双目图像间的基础矩阵；

(2)依据对极约束条件和求得的基础矩阵，计算特征点匹配集合中其它特征点对的对极约束误差，若误差在允许范围内，则认为该特征点对为内点，并统计内点的数量；

(3)判断内点数量是否超过设定阈值，若超过设定阈值，则认为当前求得的基础矩阵为最优基础矩阵，否则再从特征点匹配集合中随机抽取八个特征点对，进行新一轮的迭代计算；

(4)若迭代次数达到设定的最大允许迭代次数，则将求得内点数量最多时对应的基础矩阵作为最优基础矩阵；

(5)最优基础矩阵对应的内点即为经过RANSAC剔除误匹配点后剩下的最优匹配点。

2 双目视觉定位

利用改进ORB算法提取图像中无人机的特征点后，需要计算特征点的三维坐标，进而确定无人机的三维位置。双目视觉可以直接计算特征点的深度信息，这是因为在特征点的三维位置解算模型中，双目视觉能够提供具有实际物理意义的旋转和平移参数。

2.1 双目视觉三维定位流程

利用双目视觉进行编队无人机三维定位的流程如图2所示。首先利用双目采集无人机的图像；接着利用改进ORB算法提取双目中无人机的特征点，对特征点进行配对并读取匹配特征点的像素坐标；再将特征点的像素坐标代入到双目视觉三维定位模型中，从而得到特征点的三维坐标；最后按上述方法对所有的特征点的三维坐标加和平均处理后，作为无人机的三维坐标位置。

图2 双目视觉三维定位流程

Fig.2 Process of binocular vision 3D positioning

2

2

单目视觉投影模型是双目视觉定位中最基本的测量单元。对于单目视觉，空间场景中的特征点投影到像素平面的模型如图3所示。

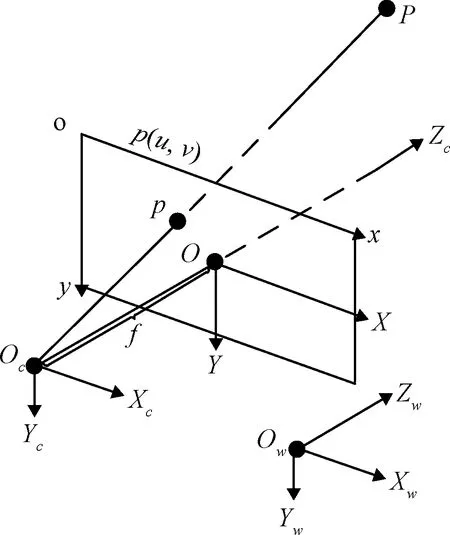
图3 单目视觉投影模型

图3所示的视觉投影模型包括4个坐标系：世界坐标系-、相机坐标系-、图像坐标系-和像素坐标系-。首先将特征点在世界坐标系中的位置(,,)投影到相机坐标系中，再投影到图像坐标系中，最后投影到像素坐标系，得到像素坐标(,)。整个过程的投影公式为

(1)

式中：为特征点的深度信息；,,,为相机矩阵参数，可通过相机标定得到；和为世界坐标系与相机坐标系间的旋转和平移；为相机内部参数矩阵；为相机外部参数矩阵；为投影矩阵。

2.3 双目视觉三维定位模型

传统的双目视觉模型利用视差原理进行特征点的定位，这就要求双目图像是共面且行对准的，而受设备制作工艺、测量误差等因素的制约，实际拍摄的双目图像很难做到共面且行对准。本文提出的双目视觉模型不要求双目图像是严格共面和行对准的，利用三角测量的方式实现特征点的三维定位，符合实际情况的需求。

双目视觉三维定位模型由两个单目视觉投影模型构成，如图4所示。对于空间场景中的特征点，其在左右双目图像中匹配的像素点分别为和，则射线和的交点即为特征点的空间位置。

图4 双目视觉三维定位模型

设和对应的像素坐标分别为(,)和(,)，对应的深度信息分别为和,和分别为左右相机的投影矩阵，则特征点与该点在左右图像上像素坐标的对应关系分别为

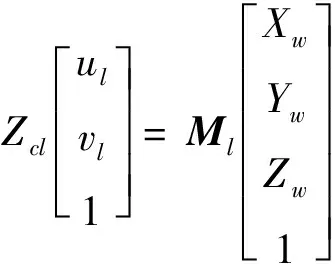
(2)

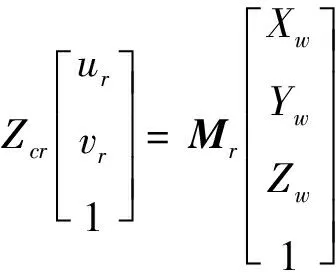
(3)

设左右相机的投影矩阵,的具体形式分别为

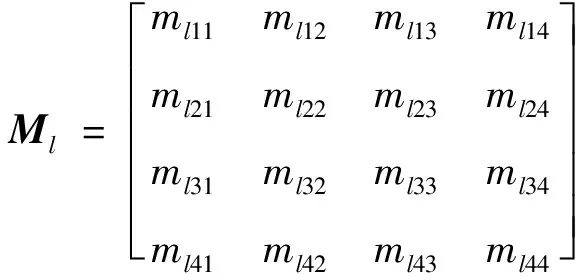
(4)

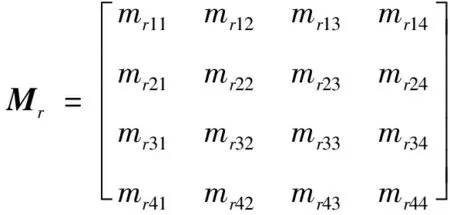
(5)

将式(4)和式(5)分别代入到式(2)和式(3)中，得

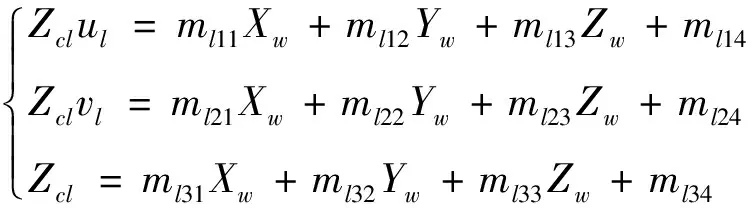
(6)

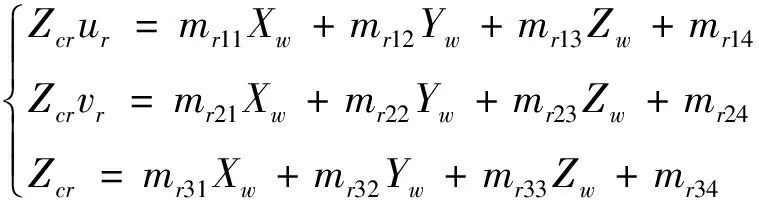
(7)

联立式(6)和式(7)，消除和，得

(8)

令

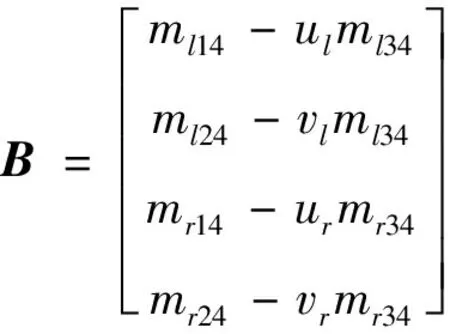
则式(8)的表达形式为

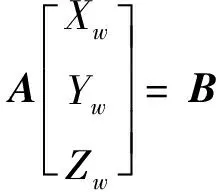
(9)

由于矩阵是4×3维的，则式(9)是关于变量,,的超定方程。理论上式(9)中某两个方程是线性相关的，但受到特征点匹配误差、图像噪声等的影响，这种线性相关性实际上不存在。线性相关性不存在的几何意义就是射线和不相交而成为异面直线。所以这里求式(9)在最小二乘意义下的解，即

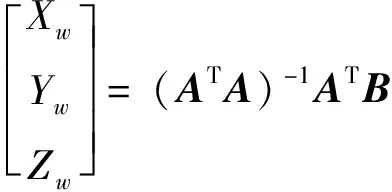
(10)

最小二乘意义下的解就是两条异面直线间的最短距离所在线段的中点，如图5所示。

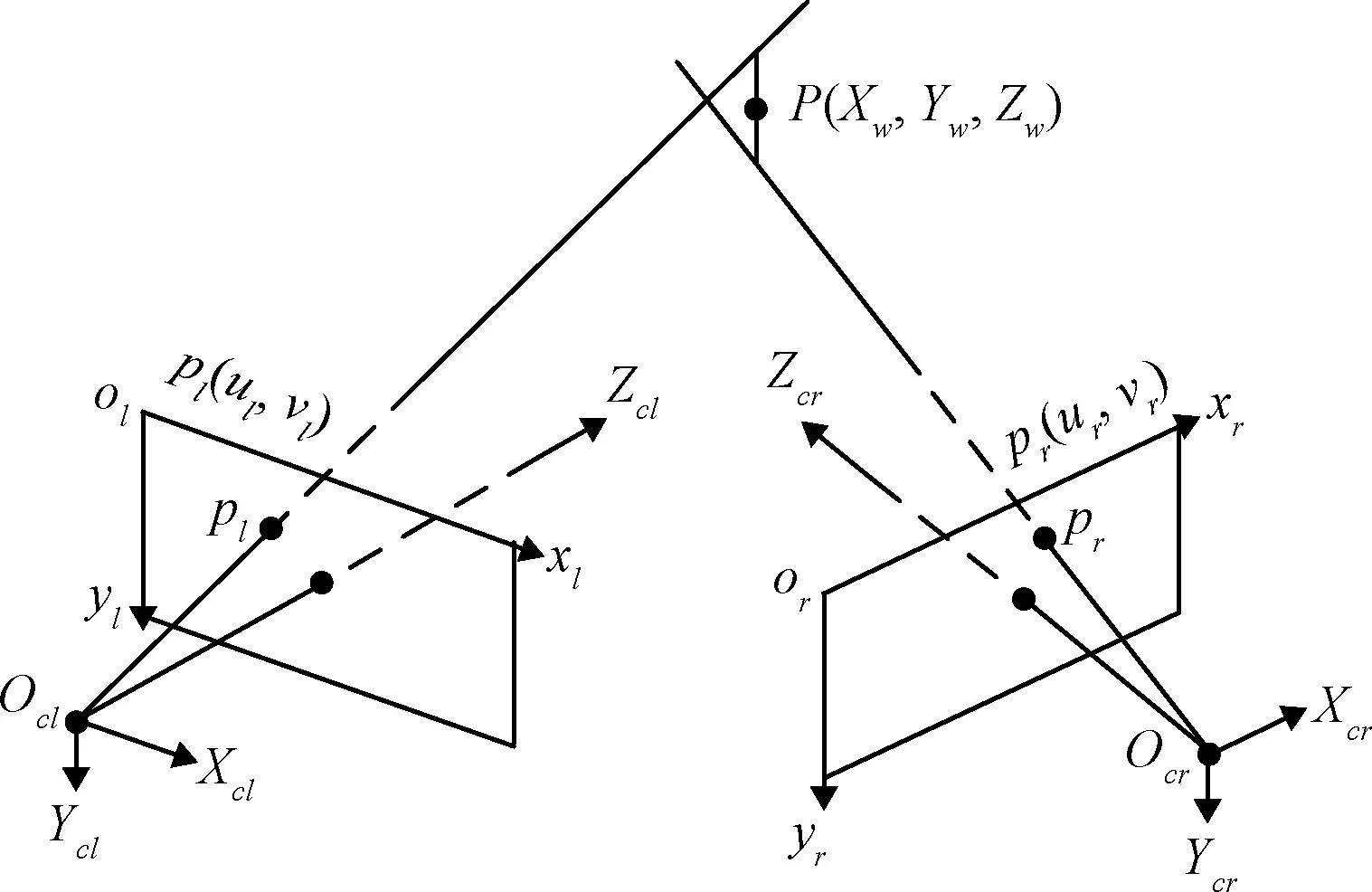
图5 最小二乘解

3 基于卡尔曼滤波的定位估计

受实验环境、实验设备调试参数、实验设备精度等因素的影响，实际的无人机三维位置与算法计算的无人机三维位置不可避免地存在一定偏差。因此，本文采用卡尔曼滤波算法对计算的无人机位置进行估计，以进一步提高无人机的定位精度。

卡尔曼滤波通过递归更新方法，对当前状态进行估计，并使状态的真实值和滤波器的估计值均方误差最小。考虑如下系统模型：

(11)

式中:为时刻的系统状态;,-1为系统状态转移矩阵;-1为噪声驱动矩阵;为状态观测量;为观测矩阵。令过程噪声-1的方差为;观测噪声的方差为。则对应式(11)所示系统模型的卡尔曼滤波步骤为：

1)状态预测：根据-1时刻状态估计值-1|-1，计算时刻状态预测值|-1，即

|-1=,-1-1|-1

(12)

2)协方差预测：根据-1时刻系统协方差-1|-1，预测时刻系统协方差|-1，即

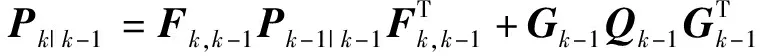
(13)

3)卡尔曼增益更新：使用|-1计算卡尔曼增益，即

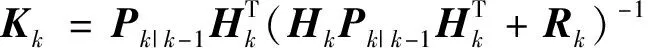
(14)

4)状态更新：根据状态的预测值和观测值，计算时刻状态估计值|，即

|=|-1+(-|-1)

(15)

5)协方差更新：求时刻状态估计值对应的协方差|，即

|=(-)|-1

(16)

当执行步骤5)后，即完成一次迭代计算，再从步骤1)重新迭代，以计算下一时刻的状态估计值。

4 实验结果与分析

本文使用的算法运行平台为华硕FX63VM笔记本电脑(Intel i5-7300HQ，2.5GHZ CPU，8GB RAM)，实验平台搭载Ubuntu16.04系统。使用MYNTEYE双目相机采集双目图像，双目图像的分辨率均为752×480，利用双目图像进行下面的实验。

4.1 改进ORB算法与传统ORB算法对比

为了验证改进ORB算法的精确性和实时性，这里对传统ORB算法与改进ORB算法的性能进行对比。利用传统ORB算法对双目图像进行特征点匹配，实验结果如图6所示。可以看出，传统ORB算法会出现特征点的错误匹配现象，而且匹配的特征点数量过多，也增加了后续在无人机目标定位时的计算量。

图6 传统ORB算法特征点匹配

改进ORB算法的特征点匹配结果如图7所示。对于采集的原始双目图像，首先提取双目图像中的无人机目标区域，如图7(a)所示；接着在无人机目标区域内进行特征点提取与匹配，并且通过最近邻约束和RANSAC方法筛选出匹配质量高的特征点对，如图7(b)所示。

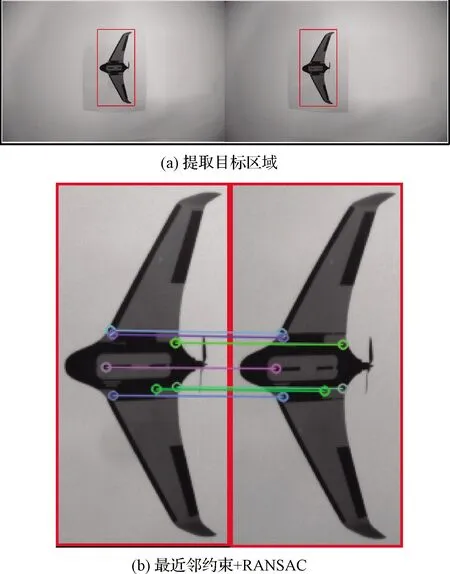
图7 改进ORB算法

传统ORB算法与改进ORB算法的具体性能指标的对比情况，见表1。

表1 两种算法的性能对比

由表1可知，相比于传统ORB算法，改进ORB算法的精确性和实时性均明显提高。由于只在目标区域内进行特征点提取与匹配，改进ORB算法避免了在非目标区域上选择无效特征点而浪费计算资源，使得运行时间仅为原来的1/3左右，运行时间只需7 ms，满足算法实时性的要求；通过最近邻约束和RANSAC方法，改进ORB算法筛除了大部分匹配质量低的和全部的交叉错误匹配特征点对，只保留少数匹配质量高的特征点对，使得特征点对的匹配正确率达到100%，满足算法精确性的要求。

4.2 目标定位

为了验证基于改进ORB算法的双目视觉定位算法的可行性，本文进行了基于双目视觉的目标定位实验。

以左目相机坐标系作为世界坐标系，即双目视觉定位系统的参考坐标系。标定目标定位实验所需的双目相机参数，包括世界坐标系与相机坐标系间的旋转和平移和、双目相机内部参数矩阵1和1。本文利用Kalibr软件标定双目相机的相关参数，见表2。

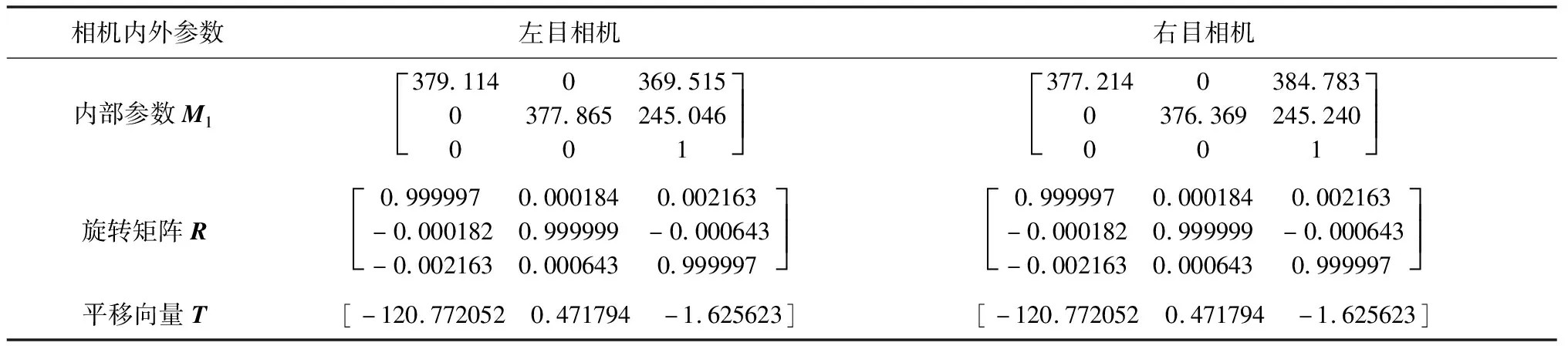
表2 双目相机参数

将目标放置在距离双目相机450 mm处，利用双目相机采集图像；然后利用改进ORB算法对双目图像中的目标无人机进行特征点提取与匹配；再将特征点的像素坐标代入到双目视觉三维定位模型中，得到特征点在世界坐标系中的三维坐标；最后求取所有特征点的三维坐标的平均值作为目标无人机的三维坐标。实验结果见表3。

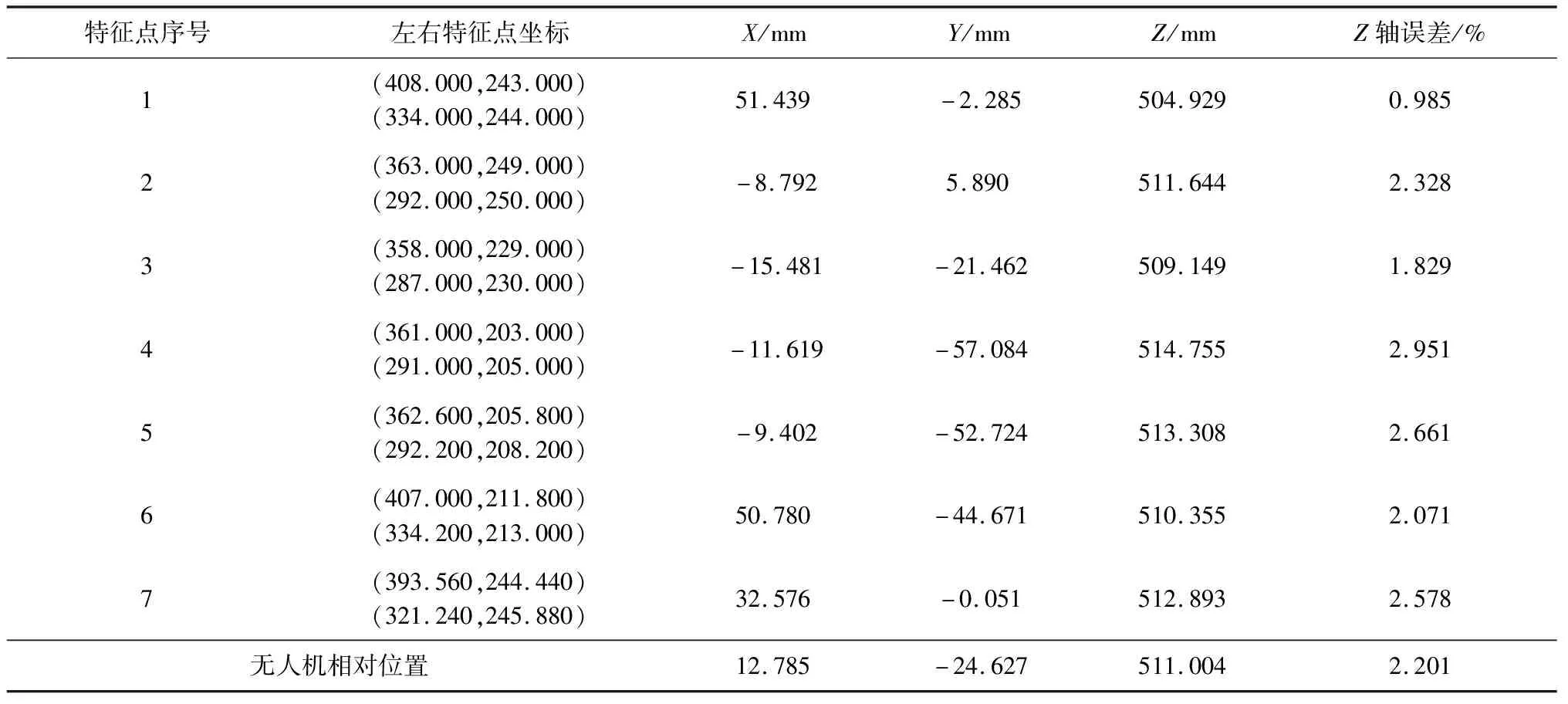
表3 三维定位结果

由表3可知，双目视觉定位系统的轴定位误差小于3%。由于特征点在世界坐标系轴和轴上的实际坐标位置难以测量，本文通过比较两个特征点间的实际距离与解算距离的差值来评判轴和轴的定位误差。最左边与最右边的特征点的实际距离为7.09 cm，解算距离为6.96 cm，可得轴定位误差为1.819%；最上边与最下边的特征点的实际距离为6.16 cm，解算距离为6.30 cm，可得轴定位误差为2.273%。经分析，产生误差的原因包括：1)通过标定得到的双目相机参数有一定偏差，导致结果不精确；2)双目相机设备精度低，图像分辨率不高，导致获取的特征点信息不精确。

4.3 基于卡尔曼滤波的定位估计

由4.2小节的实验可以看出，双目视觉定位系统仍存在一定的定位误差，采用卡尔曼滤波算法对计算的无人机位置进行估计，以进一步提高无人机的定位精度。设两架无人机在空中相对飞行，用从机的双目视觉定位系统计算的主机三维位置作为观测量，观测周期为0.1，并设双目视觉定位系统中各轴的观测噪声标准差为3%。仿真结果如图8所示。

图8 卡尔曼滤波定位估计

图8给出了双目视觉定位系统原始观测的定位误差和经过滤波处理后的定位误差。从图中可以看出，经过卡尔曼滤波估计后的定位误差大幅度减小。对图中的数据进行统计，滤波前各轴的最大定位误差为6.926%、8.885%、9.100%，滤波后各轴的最大定位误差为3.143%、2.823%、2.578%；滤波前各轴的平均定位误差为2.219%、2.433%、2.473%，滤波后各轴的平均定位误差为0.979%、0.836%、0.827%。分析数据可知，使用卡尔曼滤波算法对无人机的定位信息进行估计，能够进一步提高无人机的定位精度。

5 结 论

针对双目视觉定位时精确性低、实时性差、计算量大的问题，本文提出了一种基于特征点的无人机双目视觉定位算法。在图像特征匹配方面，对ORB算法进行了改进，通过只对目标区域进行特征点识别，使得ORB算法的计算量大幅下降，实时性显著提高；并通过最近邻约束和RANSAC方法筛选出少量高匹配质量的特征点对，提高了特征点的匹配精度，也减少了后来双目视觉定位时的计算量。在双目视觉定位方面，本文提出了更符合实际情况的双目视觉定位模型，不要求双目相机是严格的共面且行对准，同时也能保证定位的精确性，使得双目视觉定位系统中各轴的定位误差均小于3%；最后通过卡尔曼滤波算法对无人机的定位信息进行估计，进一步减小了无人机的定位误差。实验结果表明，基于特征点的无人机双目视觉定位算法具有较高的精确性和实时性，满足无人机间的相对定位要求。本论文的研究方法同样适用于视场中有多个无人机的情况，但如果存在编队中多架无人机在图像中投影重叠的现象，本文所提改进ORB算法无法有效完成不同无人机间的图像分割，进而影响无人机的定位结果。因此，在下一步工作中将研究通过人工智能手段对重叠目标进行分割的方法。