波流耦合条件下东海海域高压立管静力学分析

徐佳，徐万海

1.中海石油（中国）有限公司 上海分公司，上海 200335

2.天津大学 水利工程仿真与安全国家重点实验室，天津 300072

我国海洋油气资源丰富，但总体勘探程度相对较低。油气开发向海洋逐步推进，充分利用海洋优势，可保证我国油气资源的自给率，保障经济社会可持续发展[1-2]。

东海海域平均作业水深80～100 m，地质条件复杂，常规导管架下的模式开发经济风险较大。由于半潜式平台的作业成本远远高于自升式平台，针对浅水区（水深不超过120 m）水下生产系统的部署，使用自升式平台将会大大降低油气开发成本，而高压立管系统在自升式平台水下生产系统的钻完井作业过程中必不可少。海洋立管是海洋油气资源开发采集设备中重要的组成部分，同时也是薄弱易损构件之一。

海洋立管内部一般有高压的油或气通过，外部承受波浪、海流荷载的作用。由于立管所处海洋环境的复杂性，其影响因素也较多[3-6]。吴梓鑫等[7]采用Fluent 软件数值模拟了立管在不同波流参数数值水池中的运动，从立管受力和轴向振动等多个方面对立管在波流联合作用下的载荷响应进行研究。金瑞佳等[8]通过大比尺物理模型试验，研究了水流及波流联合作用下新型自由站立式防台风隔水立管的涡激振动。姜峰等[9]以海洋立管为模型，采用Morison 方程结合Stokes 五阶波理论计算波浪力，研究了海洋立管在波流载荷同时作用下的动力可靠性。

除了海洋环境载荷，还存在例如顶张力等因素影响着立管结构的稳定。Park等[10]采用基于Newmark 常加速度法的有限元法，对细长海洋结构在参数激励和强迫激励联合作用下的横向响应进行了数值分析。Chen等[11]采用微分变换法研究了各种边界条件下海洋立管的固有频率和振型。李艳丽等[12]采用软件Tube2D 对平台和立管进行动力响应和弯曲应力分析，得到考虑平台作用的立管扶正器布置间距参数的敏感性和立管弯曲应力的变化。马天麒等[13]建立了内部多相流-立管-外部绕流的耦合方程，对内输多相流立管在内流与外部绕流耦合作用下的振动响应进行了分析，研究发现立管内两相流会引起立管自然频率的降低，管内流速越高，立管越长，两相流作用越明显。雷松等[14]运用微分变换方法求解立管自由悬挂状态的固有频率和振型，研究发现钻井隔水立管在下水作业时，末端的悬挂器具在浅水时减小了立管固有频率，随着水深增加又增大了立管的固有频率。吴晨等[15]采用欧拉-伯努利梁模型建立立管的动力响应控制方程，应用Galerkin方法求得立管的固有频率，并研究了浮式平台的运动、张紧器的张力计算模型以及张紧器的结构参数对立管固有频率的影响。

在多种因素的影响下，立管受力极其复杂。立管结构一旦失效，会造成严重的经济损失和环境污染。为了保证海洋结构的安全，减少对生态环境的影响，本文采用有限元方法进行数值模拟，对东海海域条件下的自升式平台作业时的高压立管静态响应情况进行深入研究。

1 立管模型

在进行高压立管结构分析时，首先对立管系统模型进行简化。高压立管和其内部钻柱形成等截面的环型空间，钻柱和高压立管之间充满钻井液，钻柱和高压立管内壁不发生接触，故不考虑钻柱对高压立管弯曲刚度的影响。根据工程条件，立管不同管段间的丝扣连接和顶部防喷器的刚性密封连接均可以处理为刚性连接。同时，如图1 所示高压井口头通过液压连接器以及法兰与立管进行连接，连接构件自身强度高于立管，可作为刚性连接。

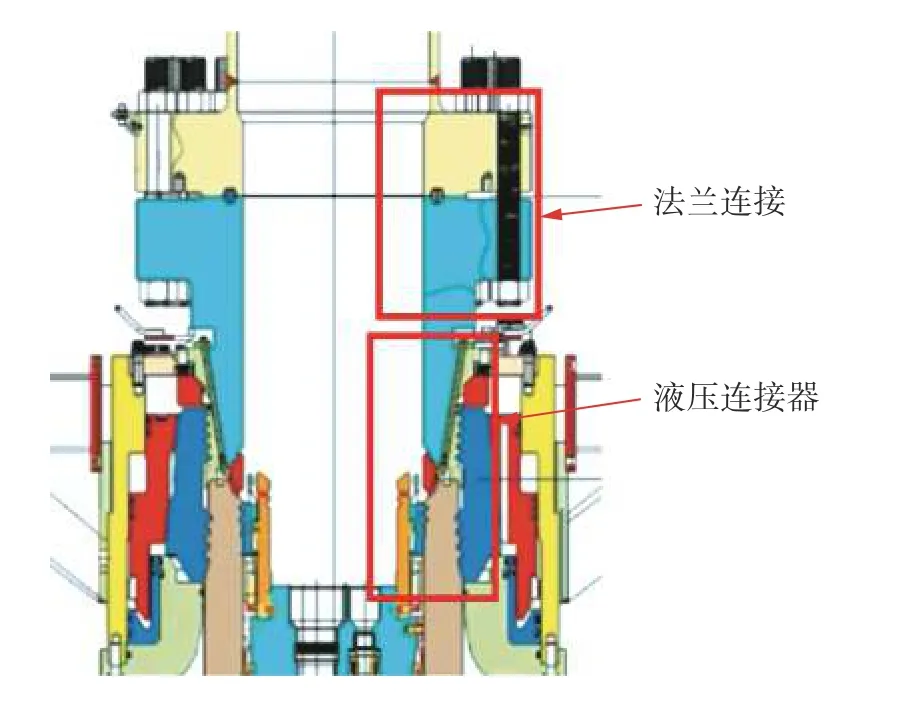
图1 井口连接方式

考虑到立管大长径比的特征，将整体结构简化为欧拉-伯努利梁模型（如图2 所示），结构运动控制方程为

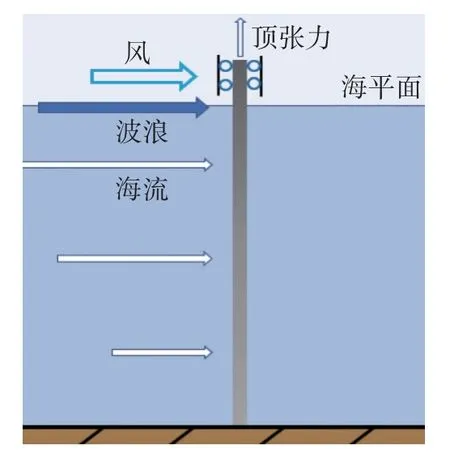
图2 立管简化模型

式中：m为单位长度总质量，y为横向结构位移，x为轴向位移，t为时间系数，C为结构阻尼，T为立管顶张力，EI为结构弯曲刚度，F为外部作用力（海平面以下主要为波浪力和流体力）。

根据海洋实际环境条件，作用在高压立管系统上的外力除重力、浮力等基本载荷外，必然还受到海洋环境载荷作用。立管作业过程中涉及的主要环境载荷包括海流载荷、波浪载荷和风载荷。根据高压立管作业海域的极端海洋环境条件，如表1 所示，计算高压立管在极端工况下的力学响应。由于台风季环境载荷远大于正常季节，所以采用的环境载荷极值均为台风季的载荷极值。根据波浪理论选取原则，采用Stokes 五阶波浪理论进行后续计算。

表1 环境载荷

2 有限元计算

确定高压立管系统基本模型后，进行结构有限元计算。首先根据工程中立管的尺寸，在ANSYS中创建几何模型。结构基本参数如表2 所示。

表2 高压立管基本参数

在有限元分析中，选用PIPE59 管单元模拟高压立管段。PIPE59 单元是一种可承受拉、压、弯作用，并且能够模拟海洋波浪和水流的单轴单元。该单元支持线性与非线性材料，可进行海洋环境载荷作用下的结构线性、非线性静力与结构线性、非线性动力分析。对单元的相关实常数进行设定，根据高压立管的材料参数定义材料属性，并在WATER TABLE 界面设置波流载荷参数。通过设置PIPE59 单元实常数，可以根据环境条件模拟作用在立管结构上的波浪及海流的外力影响，从而实现波流耦合模拟。之后在建立的几何模型基础上进行网格划分，将高压立管模型划分为有限多个单元，如图3 所示。

图3 高压立管有限元模型

选用合适的网格数量，保证能够不影响计算结果。经过计算，单元长度小于0.01L后，网格大小对结构的影响程度趋于稳定。因此，在响应计算时单元长度取为0.01L。

顶部张紧器与海上平台相连，因此上部边界可以发生转动，但在计算过程中不考虑横向偏移。因此将上部立管边界简化为简支边界。通过上述步骤建立立管系统的有限元计算模型，根据高压立管不同作业模式和工况要求施加约束和载荷，包括结构的边界条件以及相应的环境载荷，进行结构响应计算。

波浪相位角的取值对于作用于结构的波浪载荷值影响较大。因此在进行静力分析之前，需要对相位角进行搜索，以找到波流耦合力最大时的相位角取值，以此结果作为极端工况分析时的输入条件。计算得出波流耦合力最大时，相对应的波浪相位角为27°。将求得的相位角带入100 a 重现期海况进行极端海况分析，结果如表3 所示。可以看出，相位角为27°时，立管响应明显高于相位角为0°时的响应结果。该结果表明考虑波流耦合相位角的极端工况更加危险。因此，在后续的分析中，为了确保结构安全性，以最大波浪相位角进行计算。

表3 不同波浪相位角下的立管响应

3 结果分析

根据相应环境载荷计算高压立管在不同内压Pn下的响应。考虑到高压立管在实际工程中会承受较高强度的内部压力，因此针对内压对立管响应的影响进行研究。当管内进行正常钻完井作业时，管内循环内压约为20 MPa。因此，选择0、10 和20 MPa 这3 种工况模拟不同阶段的工况条件进行计算，结果如表4 所示。

表4 不同波浪相位角下的立管响应

图4 是不同重现期海况下立管最大等效应力随内压的变化情况。可以看出，内压变化对结构最大位移影响较小，但对立管结构受力产生明显影响。在相同海况下，随着内压增大，最大等效应力幅值明显增大。这种变化在1 a 重现期工况下最为显著，最大等效应力从143 MPa 增加到223 MPa，变化幅度超过50%；在100 a 重现期下最大等效应力增长也超过了10%。这说明立管的内部高压会明显改变立管响应，降低结构安全性。

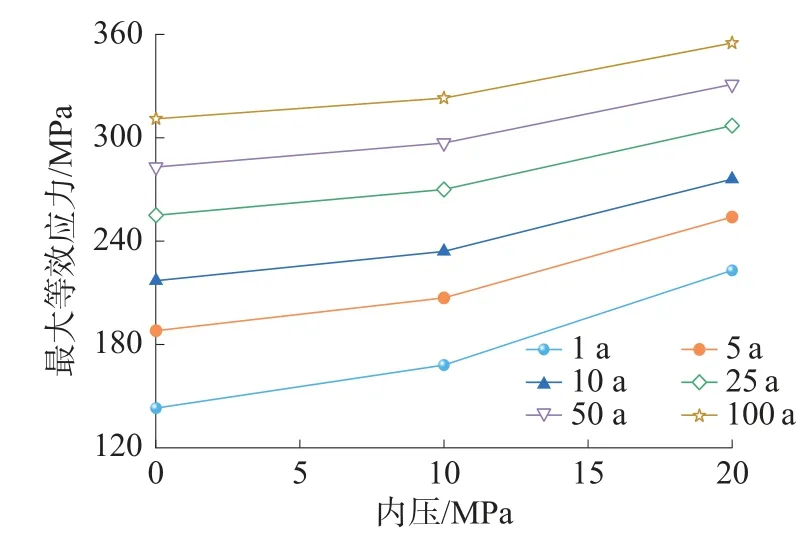
图4 不同内压下的立管最大等效应力

在相同内压条件下，海况条件越危险（重现期越长），波浪及海流载荷越大，立管静态响应也就越剧烈，结构的位移及最大等效应力幅值越大。立管主要受到波、流载荷的横向作用，因此结构主要发生横向位移。立管的应力、应变分布在不同的海况下基本相同。最大应力出现在立管根部，也就是立管与井口头连接部分，如图5 所示。在环境载荷作用下，立管接近于细长柔性体结构，在端部边界处出现了应力集中现象，影响结构稳定性。在不同工况下，这种现象均存在，并且最大应力位于底端受压面。所以在工程实际中，建议对底端进行局部加强，防止底端应力过于集中而被破坏。

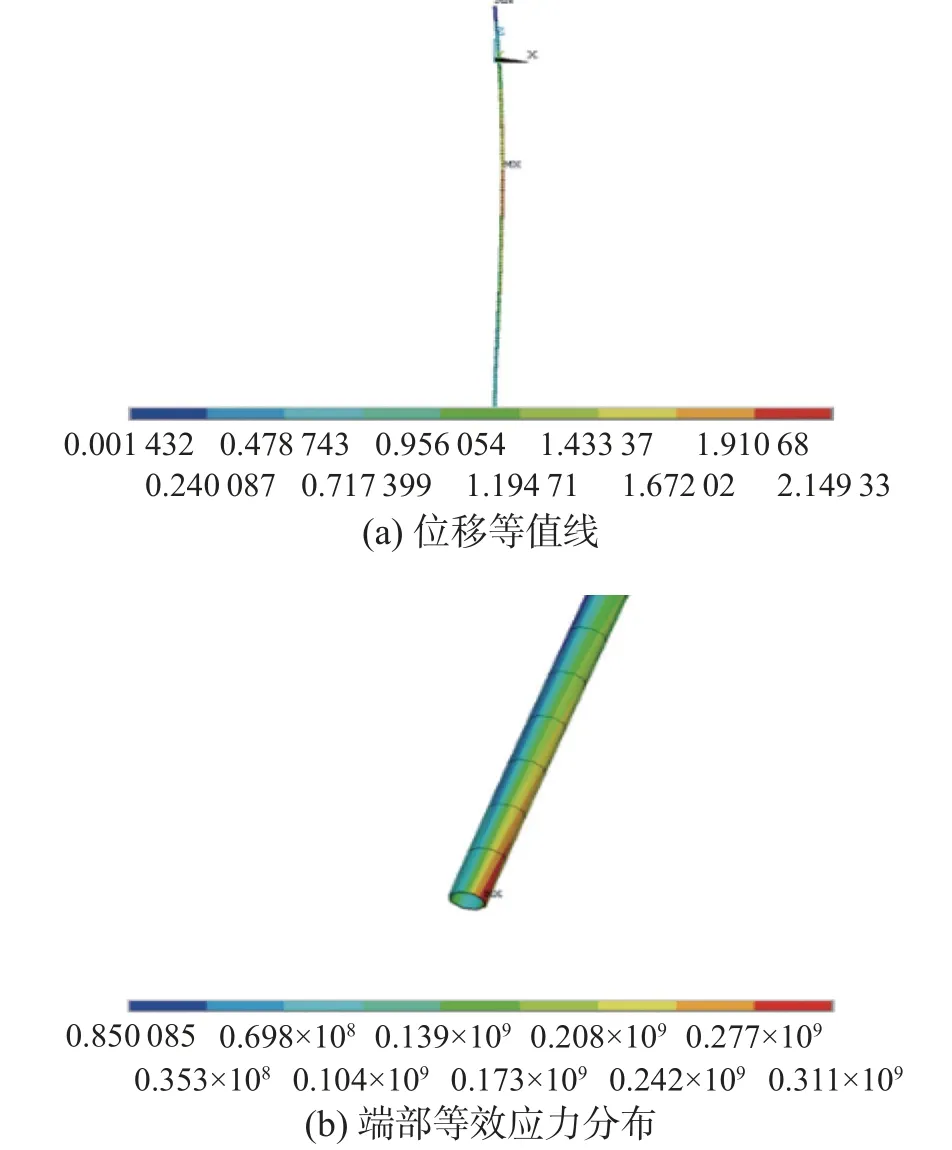
图5 响应计算结果

在极端的工况条件下，立管内可能会发生井空现象。此时立管内压达到最大，压力数值与井口压力基本相同，工程实际压力数值大约为68 MPa。因此，以70 MPa 内压条件计算立管在该极端工况下的响应，结果如表5 所示。计算结果表明，当立管内压达到最大值时，结构的最大等效应力会成倍增加，从而降低了立管结构的安全性。根据极端内压工况计算结果，井空时立管结构的响应情况已经明显超过工程安全校核的范围，结构安全性无法得到保证。

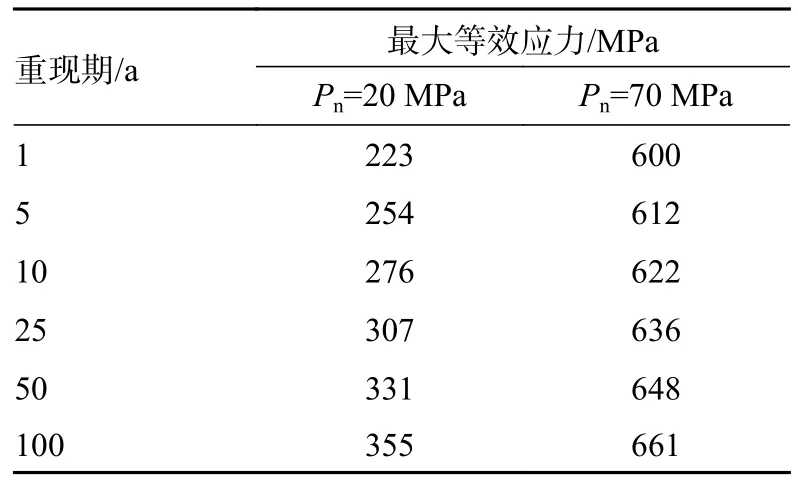
表5 极端条件下不同内压下的立管响应

在台风天气下，平台会产生横向偏移，从而可能会影响立管的受力情况。由于钻完井采用的是自升式平台，有面积巨大的桩靴插入海床以下，所以钻完井作业期间，平台几乎没有受波浪和风力影响的侧向位移，少数情况会出现插桩作业不好，导致产生沉降，出现较小的偏移。因此正常季节可以将平台的最大测量偏移量设定为0 m；对于台风季，最大测量偏移量设定为0.1～0.2 m。计算不同偏移量下的结构响应结果如图6 和图7所示。

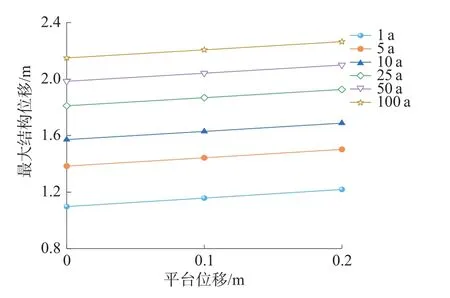
图6 不同顶端位移下的最大位移

由图6 和图7 可以看出，随着平台位移增大，立管的位移及应力幅值也相应增大，整体的变化趋势较为平稳。结果表明，顶端平台偏移量会改变立管的弯曲曲率，并直接导致结构应力增大。但由于一般条件下自升式平台较为稳定，偏移量较小，所以等效应力的变化幅值不太显著。

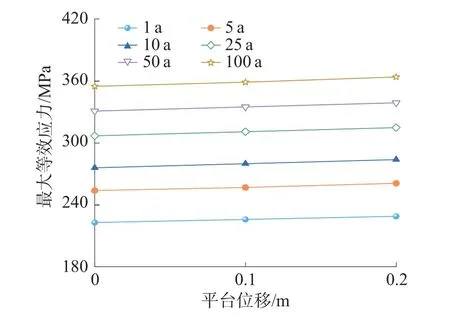
图7 不同顶端位移下的最大等效应力

极端台风工况下，平台受到极端环境的影响，会产生较大偏移幅值。根据工程经验，取极端工况下的最大偏移量为2 m，进行立管响应计算，结果如表6 所示。

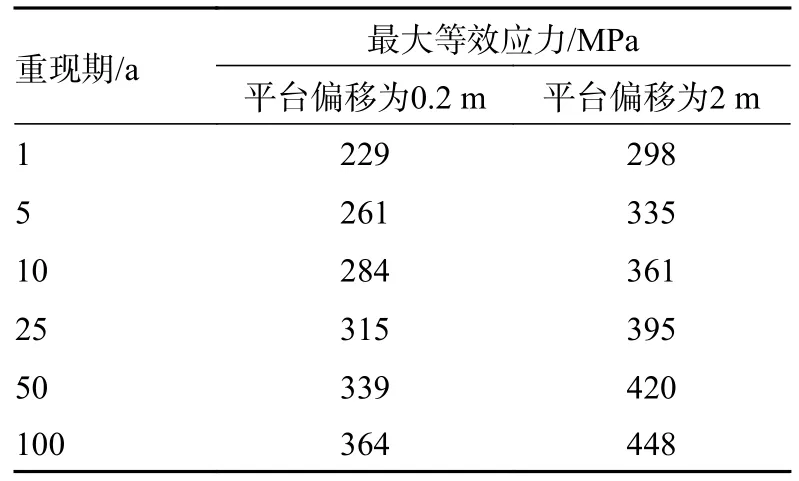
表6 极端条件下不同平台位移下立管响应

当偏移量为2 m 时，响应变化规律同一般情况类似，结构最大等效应力进一步增大，会对立管结构的受力情况产生较大影响，对稳定性的威胁较大。

4 结论

本文研究了东海海域自升式平台的高压立管静态响应情况，通过波浪载荷和海流载荷的共同影响模拟波流耦合作用，重点关注不同内压及平台偏移下的结构受力，主要结论如下：

1）随着内压的增大，结构最大位移产生较小幅度的增加，但其变化程度几乎可以忽略。最大等效应力则会发生明显增大，从而显著降低结构稳定性。

2）结构最大位移及最大等效应力随平台偏移量的增加而稳定上升。一般工况下，自升式平台的偏移对高压立管响应影响并不显著。但在极端台风工况下这种影响不可忽略。