浮式风电动态缆疲劳分析方法研究
张振国,袁振钦,孙亚峰,范艺萌,卢青针,陈金龙,尹原超
1.大连理工大学 海洋科学与技术学院,辽宁 盘锦 124221
2.江苏亨通高压电缆有限公司,江苏 苏州 215000
3.大连理工大学宁波研究院,浙江 宁波 315016
4.江苏亨通海洋光网系统有限公司,江苏 苏州 215000
5.大连理工大学 工程力学系,工业装备结构分析国家重点实验室,辽宁 大连 116081
随着潮间带及近海资源的大量开发,未来浮式风电技术将拥有更为广阔的应用前景,朝着远海化、规模化发展[1]。典型的海上浮式风电系统一般由风机、浮式平台、系泊装置和电缆组成[2]。其中,动态缆以一定线型悬挂于浮式平台下方,并连接至海底设备,为海底设备提供电力、数据及信号[3]。风电动态缆的失效风险远高于固定于桩基或敷设于海床上的静态海缆[4],尤其是在周期性海洋环境荷载作用下的疲劳失效需要得到重视。其中动态缆与浮式平台连接处的顶部位置受到较大的自重引起的拉伸荷载,同时受到恶劣工况和大幅度浮体运动引起的反复弯曲荷载,是疲劳失效的最危险部位[5]。
在动态缆的结构层中,主要抵抗拉伸载荷的铠装钢丝均采用螺旋非粘结形式,层间允许相对滑动并传递接触压力,从而使其结构具有较大轴向抗拉与径向抗压性能,同时具有较小的弯曲半径。由于动态缆螺旋缠绕单元的层数多,单元层间存在大量接触与摩擦相互作用,受到拉伸、弯曲等载荷作用时,其力学性能往往呈现更为显著的非线性特点[6]。
作为动态缆的主要受力单元,铠装钢丝层容易出现局部热点应力而最先发生疲劳,是设计分析的重点和难点。目前对于与风电动态缆类似结构特点的柔性立管和脐带缆,部分学者已进行了疲劳的相关研究。Hoffman等[7]和Jose等[8]分别基于Miner 线性累积损伤理论提出了动态柔性管缆的疲劳寿命分析流程。庞国良[9]和刘军鹏等[10]对柔性立管整体力学性能及疲劳寿命进行分析研究。Kim等[11-12]提出了考虑剪切变形与变拉力影响下的柔性立管动态响应改进分析方法,建立了更加精确的弯曲行为预测模型。Smith等[13]建立了柔性立管弹塑性三维分析模型,考虑了立管的弯曲滞回效应,计算出在疲劳荷载下铠装钢丝的内部应力时程。Skeie等[14]基于脐带缆螺旋缠绕层的滑移理论,与弯曲滞回行为建立了应力分析的理论模型,并对动态脐带缆进行了疲劳寿命分析,指出是否考虑层间的摩擦力将极大影响动态脐带缆疲劳寿命。Hoffman等[15]建立了考虑结构动态响应和构件之间接触摩擦的钢管动态脐带缆疲劳寿命预测模型。de Sousa等[16]建立了柔性立管疲劳应力分析的理论方法,将疲劳危险点处的荷载分解为拉伸荷载、弯曲荷载与层间作用,分别求解出不同荷载下的应力状态并进行了叠加。其研究表明,层间摩擦、环向荷载会严重影响柔性管的局部应力与疲劳寿命。Lan等[17]通过ABAQUS 有限元软件建立了柔性立管的数值模型,进行了往复拉伸、内外压荷载的加载与应力计算。
综上所述,目前国内外大部分研究都集中于柔性立管与动态脐带缆,关于浮式风电动态缆的疲劳分析方法研究仍然不够全面。因此,本文提出了一种实用的浮式风电动态缆疲劳寿命分析方法。通过在Orcaflex 软件中建立动态缆整体分析模型并进行时域分析,确定荷载时程与疲劳失效危险位置;随后依据动态缆的螺旋缠绕结构形式,应用非线性局部应力模型开展应力分析,计算得到动态缆内部关键构件铠装钢丝的局部应力;最后采用Miner 线性损伤理论,通过得到的各工况应力幅值及其循环次数,计算累积损伤并预测动态缆的疲劳寿命。以应用于南海某70 m 水深的浮式风电动态缆为例开展疲劳分析,结果表明,动态缆的疲劳寿命预测为46.9 a,满足25 a 的使用寿命要求。
1 动态缆疲劳寿命分析方法
浮式风电动态缆的疲劳寿命分析方法可分为3 个步骤,分别是整体荷载分析、非线性局部应力分析与疲劳寿命计算,具体的 分析流程如图1 所示。
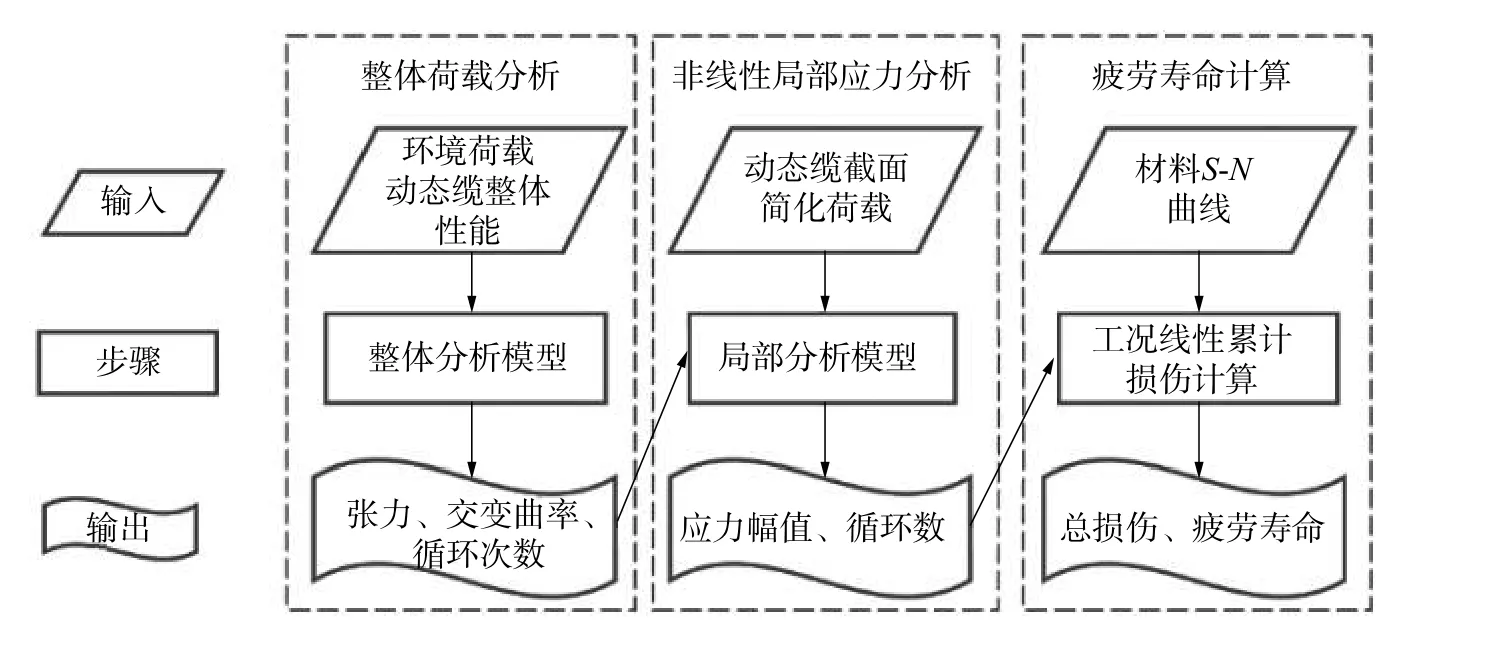
图1 浮式风电动态缆疲劳分析方法
1.1 整体荷载分析
整体荷载分析的目的是将动态缆所承受的外部环境荷载信息转化为缆体疲劳失效危险位置的荷载,包括波浪荷载、流荷载、海生物附着和浮体运动响应等多种荷载因素。Orcaflex 软件是可用于海洋工程静、动态分析并提供全三维的非线性时域分析的有限元软件。可根据动态缆所处的海洋环境,在Orcaflex 中建立动态缆整体分析模型,通过集中质量单元的方法简化有限元模型,以质量/刚度进行等效并进行时域计算。整体分析步骤如下:
1)收集与处理动态缆在位工况下的外部环境荷载信息,包括波浪荷载、流荷载以及风荷载等。
2)根据动态缆、防弯器、浮筒的结构参数设计动态缆线型并建立结构整体分析模型,如图2所示。
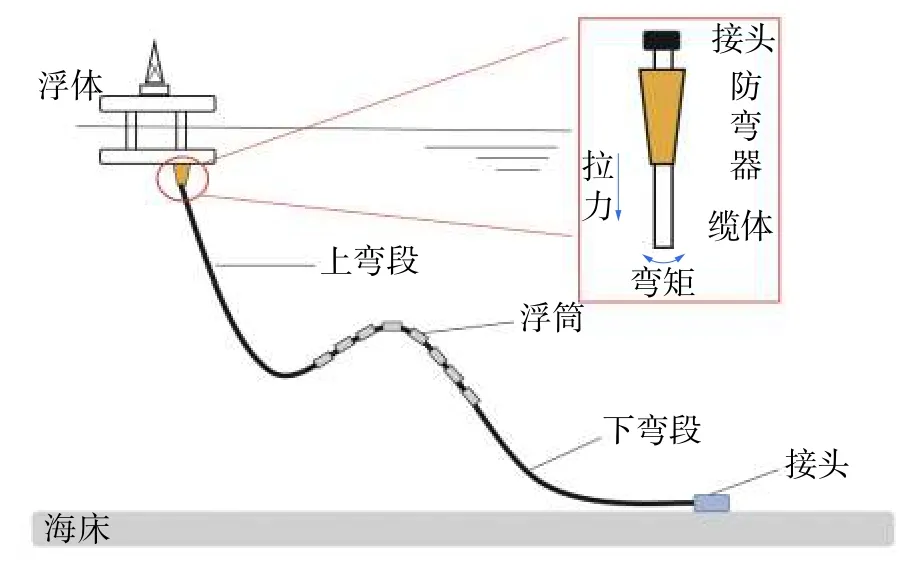
图2 风电系统整体
3)模拟动态缆在真实工况下的动态响应,定位疲劳失效危险位置,确定荷载响应时程,将其作为后续局部应力分析的输入量。
设计外部荷载参数时,需要重点考虑波浪与浮体运动响应的影响。在海洋工程领域,通常采用随机分析方法,将实际海面上不规则波视为很多简单波的叠加(即波浪谱)来描述波浪荷载的响应特征。基于Longuet-Higgins 方程,将给定的不规则波联合概率分布离散为规则波的波浪散布图,采用规则波计算波浪散布图中的工况。即1 a内某种工况实际发生次数的计算公式为
式中:P为第i种工况一年之内发生次数的概率百分比;Tzi为第i种工况的周期;ni为第i种工况一年之内的实际发生次数。对于浮体的处理,目前比较通用的做法是直接获取浮体的运动响应(response amplitude operator,RAO)作为动态边界加于脐带缆上。
通过Orcaflex 的动态分析功能,获得动态缆在各个工况下任意点的曲率时程、有效张力时程与循环次数,同时导出曲率分布曲线,确定疲劳失效危险位置。以上参数将作为输入量用于后续的非线性局部应力分析。
1.2 非线性局部应力分析
局部应力分析的目的是将整体分析得到的曲率、荷载信息分析得到内部单元应力,用于后续的疲劳损伤分析与寿命计算。在非线性局部应力分析的过程中,缆体内部构件之间的摩擦力和弯曲滞回效应会极大影响分析结果的准确性,需要在应力分析模型中重点考虑。
除了护套层、电缆、光缆及填充外,还需采用2 层或4 层铠装钢丝螺旋缠绕的形式进行铠装加强,如图3 所示。

图3 典型的浮式风电动态缆结构形式
对以铠装钢丝为代表的单层螺旋缠绕单元进行弯曲行为分析。铠装钢丝的局部应力组合可表示为轴向应力、弯曲应力以及摩擦应力,即
式中:σT为铠装钢丝的轴向应力,σB为弯曲应力,σf为铠装钢丝的摩擦应力。其中轴向应力是由动态缆结构及钢丝单元的拉伸刚度决定的,整体呈线性变化。
动态缆在位情况下通常会承受拉伸与弯曲共同荷载作用,拉力会引起较大的层间环向挤压力,导致钢丝层间存在一定的摩擦力,使动态缆的弯曲行为呈现非线性,因此非线性局部应力主要表现为弯曲应力与摩擦应力的和。
铠装钢丝层在受到弯曲荷载作用时,随着曲率的逐渐增加,最先从中性层处开始发生滑移,随后沿缠绕圆柱环向向弯曲方向的两侧逐步发生滑动,同时其局部应力会呈现出明显的非线性。钢丝单元的弯曲行为如图4 所示。
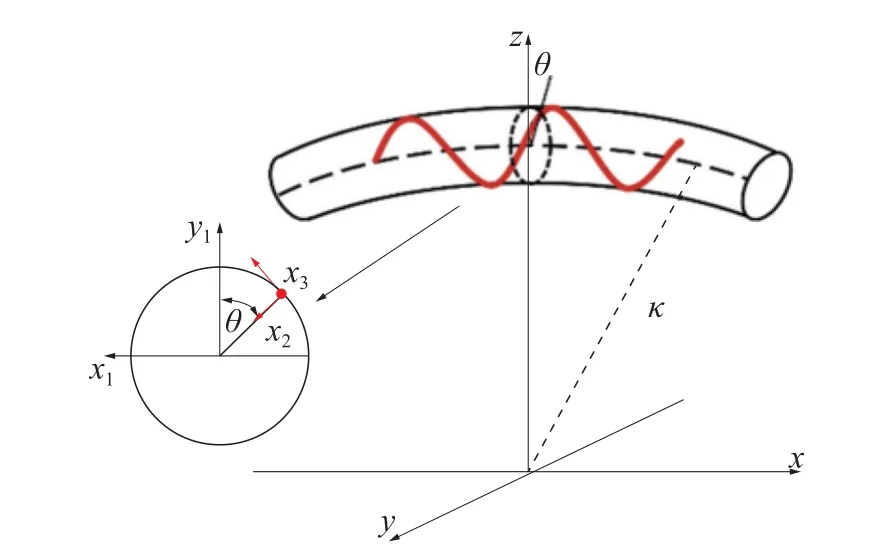
图4 单根铠装钢丝弯曲示意
基于Witz and Tan 公式[18],作者认为弯曲后的单根钢丝是沿其初始螺旋角度滑动,钢丝各个方向曲率为其对应圆柱曲率上的投影。因此可确定单根钢丝发生滑动时,临界滑移曲率为
式中:fi为第i层铠装钢丝所承受摩擦力的合力,E为铠装钢丝的弹性模量,α为螺旋缠绕角度,R为铠装钢丝的螺旋缠绕半径,A为铠装钢丝的横截面积,κcr为临界滑移曲率。
弯曲应力可根据弯曲方向不同分为弯曲正应力和弯曲切应力,弯曲正应力 σn与弯曲切应力σt可表示为曲率κ的函数:
单元的摩擦应力可表示为
在同一单元层,由于钢丝单元的滑动是由中性轴向两侧扩展,因此当该单元的相位角为0°时,距离中性层最远,单元应力也最大。可得到每层单元中最大的非线性应力为
式中r为铠装钢丝半径。钢丝单元的非线性局部应力模型如图5 所示。
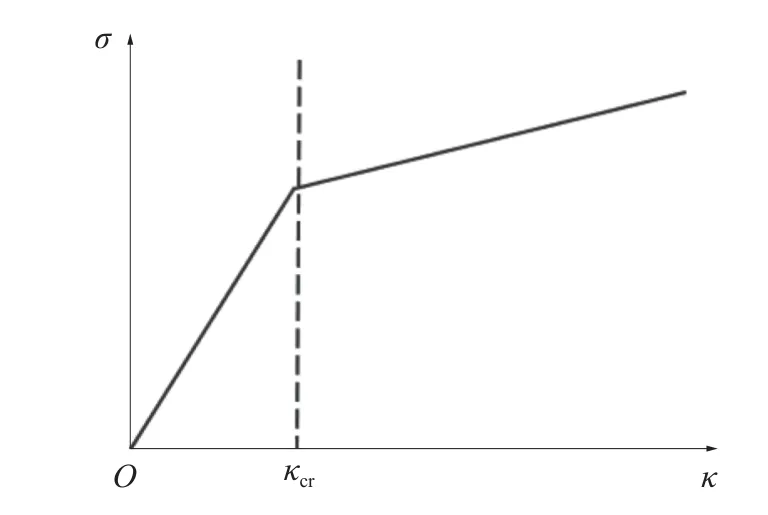
图5 钢丝单元非线性局部应力模型
选取铠装钢丝各单元中最大的非线性应力作为疲劳计算中的关键局部应力,并将此应力幅值和对应的循环次数用于后续的疲劳损伤分析与寿命计算。
1.3 疲劳寿命计算
动态缆的疲劳失效分析基于金属疲劳失效理论,根据铠装钢丝层应力状态开展时域分析,进行疲劳寿命计算。应力寿命法由于分析过程中所涉及的参数少、分析简便以及经验性强,成为当前工程界中应用最为广泛的疲劳寿命分析方法。应力寿命法以材料或零件的S-N曲线为基础,SN曲线是表示一定循环特征下标准试件的疲劳强度与疲劳寿命之间关系的曲线,来源于大量的试验统计,其数学表达式通常写为幂函数的对数形式,且具有对数线性关系,可表示为
式中:Δσi为交变应力幅值,Ni交变应力Δσi循环的破坏次数;a、m为材料参数,通常由疲劳试验获得。
本文所采用的钢丝材料S-N曲线所需参数如表1 所示[19]。

表1 铠装钢丝S-N 曲线参数
材料的疲劳数据是在对称循环条件下得到的,在实际应用中,动态缆内部单元构件承担的是非对称循环荷载,其应力是由1 个交变应力分量与1 个平均应力分量叠加而成。此时需要采用应力修正方法估算出缆体内部构件材料在不同应力比与平均应力条件下的疲劳极限。本文选用结果较为保守的Goodman 修正公式[20]对疲劳极限曲线进行简化并修正平均应力:
式中σref为材料强度极限。
通过疲劳损伤累积理论,可将修正后的应力幅值以及循环次数折算为结构损伤。根据Miner法则,不同应力幅值的荷载所造成损伤互不影响,并可以线性累积得到总的损伤,如图6 所示。
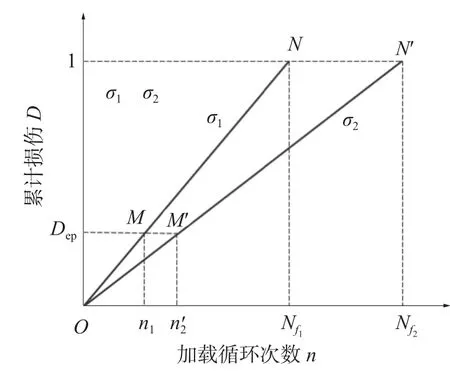
图6 Miner 法则损伤曲线
基于这一法则,动态缆结构疲劳损伤可表示为
式中:N为工况的个数;D为疲劳损伤累积量,当D=1 时,说明发生疲劳破坏,当D=0 时没有产生疲劳损伤;ni是实际循环次数。结构的疲劳寿命nlife倒数为
式中nAFD为累积疲劳损伤值(accumulated fatigue damage,AFD)。利用基于S-N曲线的Miner 线性累积损伤准则,可以简便快捷地进行动态缆的疲劳寿命预测。需要注意的是,依据与动态缆结构形式类似的脐带缆疲劳设计规范API-17B[21]的推荐,需考虑10 倍或以上的安全系数进行疲劳寿命预测。
2 应用实例分析
以我国南海某设计水深为70 m 浮式风电动态缆为例,截面结构如图7 所示。根据浮式风电基础参数与动态缆所在海域的荷载情况对动态缆进行线型设计并进行整体荷载分析。
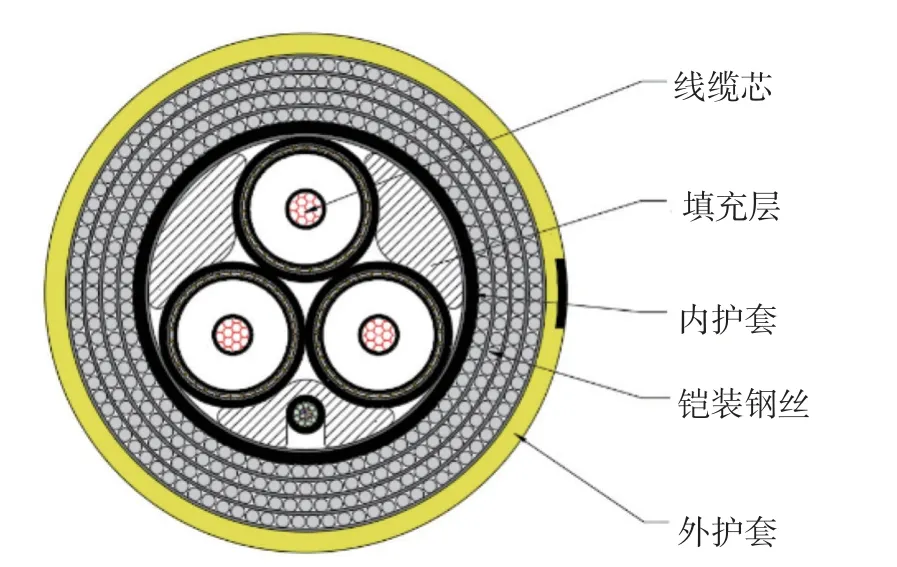
图7 风电动态缆结构示意
可根据相同高度处全风速段下波高与流向的概率分布,在每个流向下选择3 种流速,将低于这3 个速度的流速的概率累积计入对应流速;在每个流速下选择发生概率较大的6 个方向,并将其余方向发生概率分别计入30°、180°这2 个方向,流荷载分布概率结果如表2 所示。
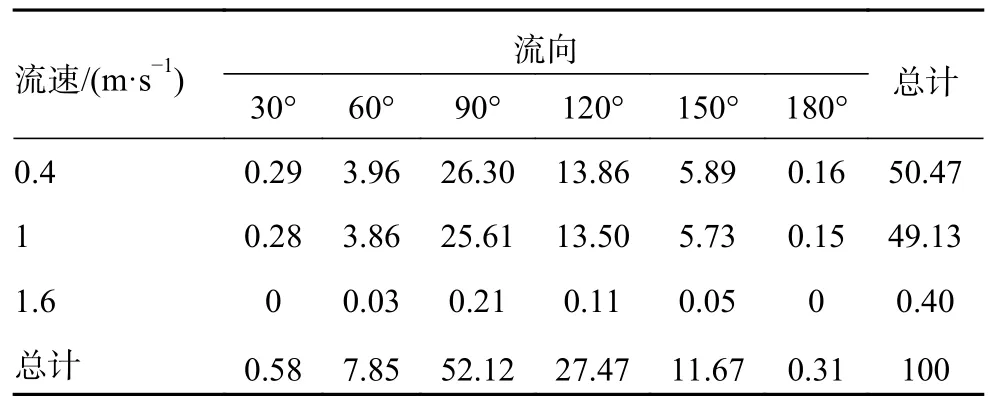
表2 流荷载的分布概率 %
风荷载参数的分布概率的选取方法与流荷载选取方法一致,选择发生概率较大的3 种风速以及5 种风向,并将低于选取风速或不同风向的概率累积计入对应风速风向,风荷载分布概率结果如表3 所示。
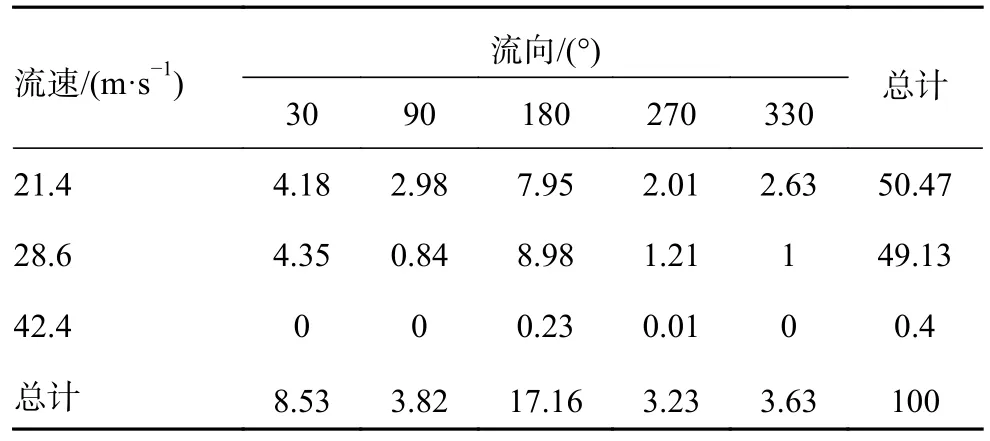
表3 风荷载的分布概率 %
为了准确描述动态缆的波浪荷载响应,通常采用随机分析的方法将实际海面上不规则波浪视为很多简单波的叠加。通过海况统计得到风电动态缆所在平台在位工况下的全年波浪玫瑰图,如图8 所示。观测海域的常浪向为E 向,次常浪向为ESE 向,频率分别41.1%和26.1%;浪向主要分布在东偏北(ENE)22.5°——东南(SE)向之间;在其他方向出现频率较少,一般不超过4%。
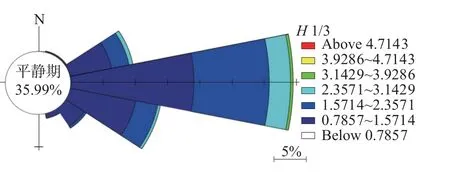
图8 动态缆在位工况下全年波浪玫瑰图
根据Longuet-Higgins 方程可以将浮式风电动态缆所在工况的连续不规则波浪散布分解为单个间断规则波的散布,从给定工况的概率分布中选择间隔为1 m 的6 个波高,间隔3 s 的8 个波浪周期,将该工况分解为31 个规则波,并将波高与谱峰周期的概率分布转化得到规则波散布工况,转化覆盖率达98.1%,如表4 所示。表中数字代表规则波在确定时间内出现的次数。
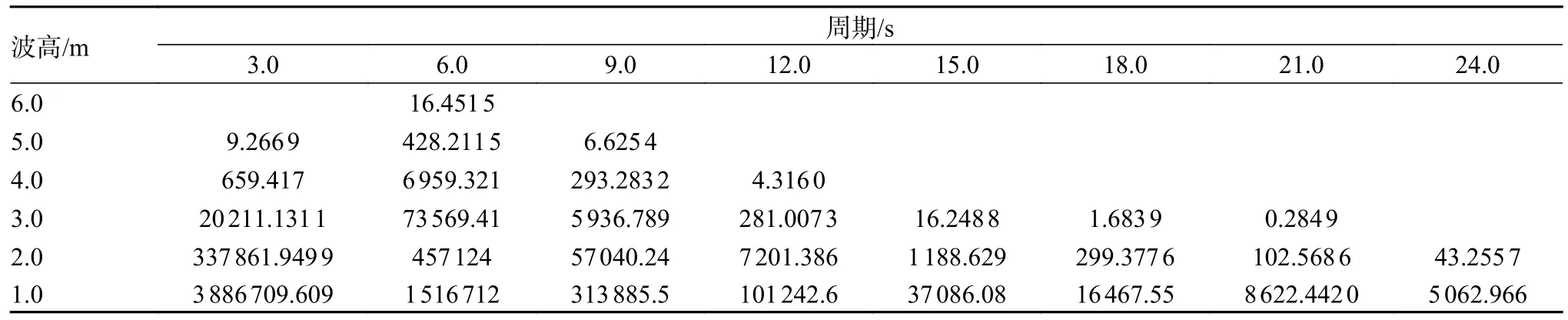
表4 动态缆疲劳计算规则波工况
为了保障风电动态缆安全运行,需要在缆体上弯段与浮体连接处安装防弯器从而避免缆体过度弯曲出现应力集中,并采用浮力装备来保持管缆线型,这种布置可以有效地减小动态缆的上部悬挂张力,使其在水中拥有良好的顺应性,有效提高动态缆的使用寿命。因此整体设计分析中需要采用防弯器与浮力模块2 种附件。风电系统的结构参数如表5 所示。
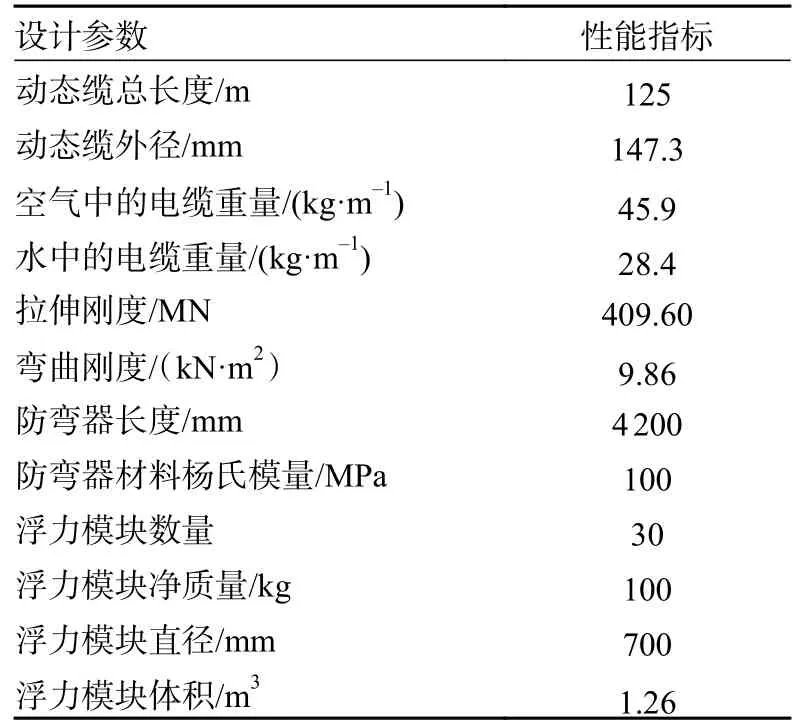
表5 风电系统结构参数
根据上述环境参数以及风电系统的结构参数,采用缓S 型线型的布置方式,借助分析软件Orcaflex 建立动态缆整体分析模型,如图9 所示。
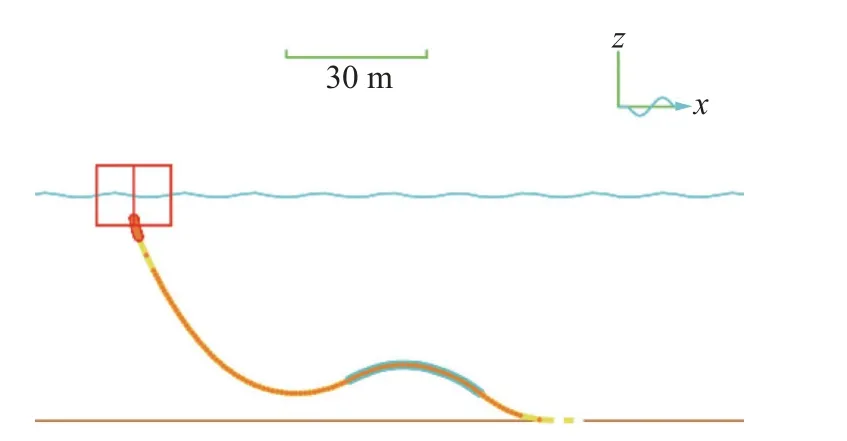
图9 Orcaflex 软件的动态缆整体分析模型
在动态分析中采用了Jonswap 波谱模拟波浪的时程,采用隐式时域方法对动态缆进行动态分析,输出不同工况下有效张力及曲率沿动态缆缆长的分布情况,其中某工况下动态缆曲率沿缆长方向的分布曲线如图10 所示。
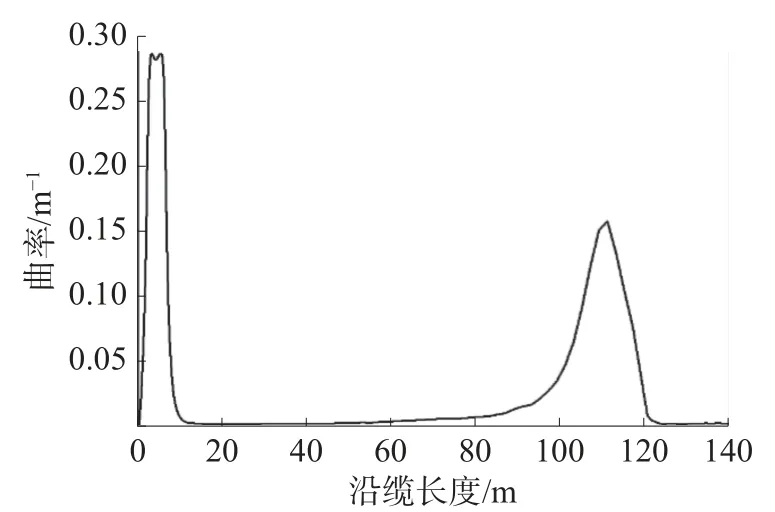
图10 曲率沿动态缆长度方向分布
通过对比曲率幅值,可得到距浮体连接3.3 m处是整个风电动态缆的疲劳失效危险位置,这是由于顶部连接点会受到大的张力与弯矩的共同作用。
利用规则波法选取6 390 个规则波工况,如图11 所示。动态缆的平均拉伸荷载为14.5 kN。
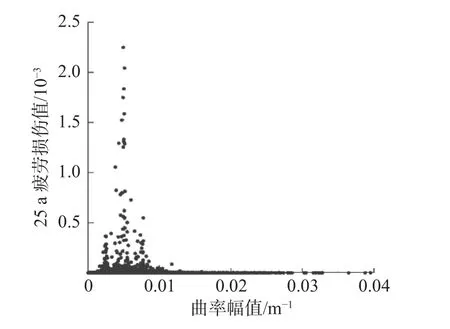
图11 动态缆各规则波工况交变曲率与对应的疲劳损伤
由于Orcaflex 软件计算时采用了线性的应力系数,会导致应力计算结果偏小。较为可靠的方法是通过Orcaflex 软件输出各工况下风电动态缆承受的拉伸荷载与曲率分布情况,可利用非线性应力模型进行二次计算得到风电动态缆内部单元上的应力。根据API-17B 规范,将损伤散点图按照曲率幅值划分为不少于4 个以上模块,从中筛选出损伤最大值的点作为该模块的代表性工况。选取数据结果如表6 所示。
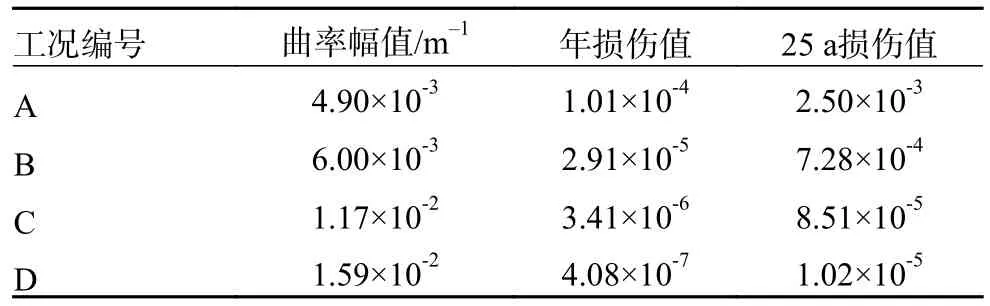
表6 动态疲劳分析工况选定
根据式(1)和式(2)可计算得到动态缆铠装钢丝滑动时的临界曲率值为0.007 m-1;利用非线性局部应力模型将表6 中筛选得到的代表工况曲率幅值代入式(3)中,计算铠装钢丝层螺旋单元上的真实应力情况,得到钢丝随曲率变化的非线性局部应力;经平均应力公式(5)进行平均应力修正,得到的应力结果代入式(4)中得到循环次数,通过式(6)获得各工况下动态缆疲劳失效危险位置的疲劳损伤。
基于表1 中铠装钢丝材料S-N曲线参数可计算各工况下的疲劳损伤,从而获得考虑非线性局部应力影响的动态缆疲劳寿命为46.9 a,满足25 a的使用寿命要求。
3 结论
本文考虑动态缆螺旋缠绕结构特征引起的截面非线性局部应力的影响,将非线性应力分析方法加入到疲劳寿命分析方法中,并代入实例进行准确性分析。采用理论与数值结合的手段对浮式风电动态缆的疲劳寿命预测进行研究,得到如下结论:
1)基于Miner 线性损伤累积理论,提出了一种更适用动态缆的非线性应力疲劳分析方法,可以得到更准确的疲劳寿命结果。
2)针对我国南海某70 m 水深的浮式风电动态缆为例开展疲劳寿命分析,较为准确地得到动态缆的疲劳寿命预测,为动态缆抗疲劳设计及工程应用提供可行的分析方法。

