考虑储能装置容量安全差值的日前优化调度

辛月杰， 周云海， 贾倩， 张韬

(三峡大学电气与新能源学院， 宜昌 443002)

2021年“两会”期间，“碳达峰”和“碳中和”[1]话题被提升到战略性高度。目前电力行业的 CO2排放量占中国碳排放总量的50%左右，为大幅降低碳排放，尽快实现“双碳”目标，对电力行业改进是必要且迫切的[2]。目前由新能源配合火电机组作为主要改进方式之一，来降低 “碳排放”。但由于新能源出力具有随机性和波动性的特点[3-4]，加之中国电源结构以燃煤机组为主，系统运行灵活性不足，这使得大规模风光消纳面临挑战[5]，给实现“双碳”目标造成困难。抽水蓄能电站具有建造规模大、技术水平高、经济成本优的特点[6-8]。蓄电池能够在短时间内保证稳定运行，同时可改善输出电能质量[9]。两者作为电能在时间上的转移手段，可弥补新能源出力的波动性和随机性带来的不足[10]，有效解决新能源并网“瓶颈”问题，提升系统运行水平[11]。

中外学者对于储能装置参与新能源消纳，已经做了大量研究，并取得一定成果。文献[12-13]以风蓄联合运行的调峰效益和电量效益、风电功率波动等为目标函数，建立了风电-抽水蓄能联合运行的优化调度模型，确定了抽水蓄能对促进风电消纳的效用。文献[14]以火电机组的燃料费用最低为目标，提出量化分析抽水蓄能提升可再生能源消纳效果的计算方法，对“风光+抽蓄”联合运行模式进行探索。文献[15]建立源荷储多种灵活性资源统一协调滚动调度模型，优化每个时段中的各类机组出力状况，但在优化过程中仅考虑抽水蓄能一类储能装置的优化作用，缺乏对多类储能装置的研究。文献[16-20]大规模蓄电池储能系统以其独特的优势在削峰填谷方面发挥了巨大作用。上述研究主要集中于对单类储能装置参与优化时的削峰填谷作用，未针对多种储能装置共同参与优化时对系统的效用，也未对储能装置的容量本身做出限制。

基于此，现同时把抽水蓄能电站和蓄电池纳入优化过程，研究不同储能装置的出力状况。结合实际情况，提出在日前优化调度中，将抽水蓄能水库和蓄电池初始时刻和最终时刻容量设置一定的安全差值。将抽水蓄能电站中的机组作为单独的优化变量，构建日前优化调度模型。最终运用混合整数线性规划法对模型求解，合理安排每台机组的工作顺序。求解结果与传统的始末时刻容量一致的优化结果进行对比，突出对储能装置容量设置安全差值的效用。算例验证本文提出的研究方法，对实际生产活动具有重要意义。

1 新能源随机预测模型

当前风电和光伏的装机容量逐年递增，同时其输出功率受季节、地理位置及气候等因素的影响，对电网的稳定、经济运行提出了挑战。调度中心需要在历史数据的基础上，对其输出功率重新进行合理有效的预测，并根据预测的结果制订日前优化调度计划。重新预测的输出功率由其历史数据和偏差量构成，即

Py,t=Ps,t+Pc,t

(1)

式(1)中：Py,t为预测日t时段的风电和光伏的预测出力；Ps,t为预测日t时段的风电和光伏上报的数据；Pc,t为预测日t时段的风电和光伏的偏差量。

风电和光伏的偏差量为服从正态分布的随机变量，即Pc,t～N(μ,δ2)，如图1所示。

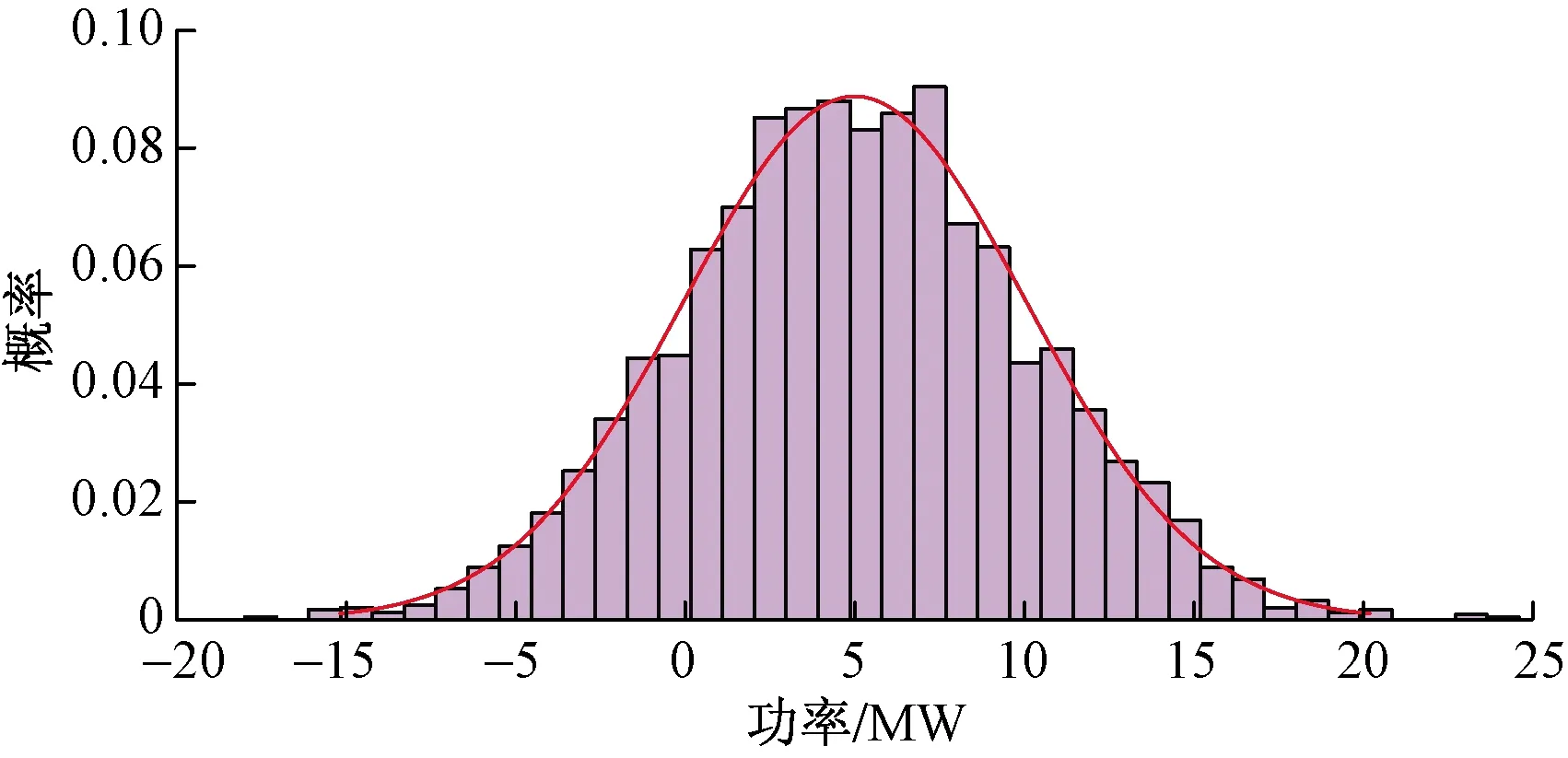
图1 风力和光伏发电量偏差正态分布Fig.1 The deviation of wind power and photovoltaic power generation is normally distributed

风电和光伏的偏差量的概率密度函数为

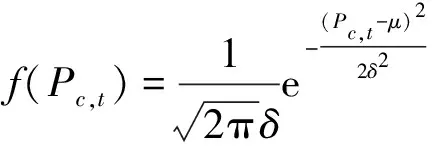
(2)

式(2)中：μ为预测误差的期望，取值为0；δ为预测误差的标准差。

2 优化调度模型

根据参与日前优化过程中电源的运行成本设立目标函数，结合各类电源之间的相互约束条件和电源本身的约束条件，构建日前优化调度模型。本文所建立的模型将1 d作为1个周期，共分为96时段，每个交易时段持续15 min，如图2所示。

经过优化计算，最终得到各类电源的出力结果，据此可以合理地安排机组的出力顺序。

图2 日前优化调度时间尺度Fig.2 Day-ahead optimization scheduling time scale

2.1 目标函数

在目前优化调度过程中，考虑系统发电的经济性，以电力系统整体运行成本最小为目标。

minC=min[Cg+Cq+Cp+Cx]

(3)

式(3)中：C为在日前优化过程中的系统整体运行成本；Cg为火电机组总运行成本；Cq为系统弃电成本；Cp为抽水蓄能电站总运行成本；Cx为蓄电池运行成本。

(1)火电机组运行成本。火电机组的开停机非短期过程，因此在日前优化中不再单独考虑火电机组的开停机成本，只考虑火电机组的煤耗成本。

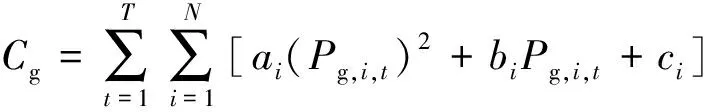
(4)

式(4)中：T为优化时段数；N为火电机组数量；Pg,i,t为火电机组i在t时段功率；ai、bi和ci为火电机组i的煤耗特征系数。

(2)弃电成本。在可再生能源的消纳过程中，一般将风电和光伏作为优化变量，其弃电成本可表示为弃风与弃光成本之和。

(5)

式(5)中：ξw和ξv分别为弃风和弃光的惩罚系数；Pwy,t和Pvy,t为预测日时段t的风电和光伏预测输出功率；Pw,t和Pv,t为优化后在时段t的风电和光伏实际功率。

(3)抽水蓄能电站运行成本。抽水蓄能电站内部每台机组在进行抽水和发电启动机时存在消耗，且在正常运行时，每台机组存在运行成本。

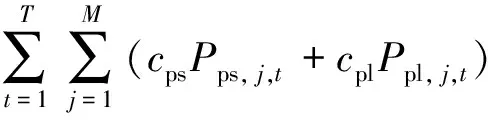
(6)

式(6)中：M为抽水蓄能电站中机组数量；cps,u和cpl,u分别为发电和抽水机组的启动成本；nps,u和npl,u分别为某一优化内发电和抽水机组的启动数量；cps和cpl分别为抽水蓄能机组发电和抽水的运行成本；Pps,j,t和Ppl,j,t分别为抽水蓄能机组j在时段t发电和抽水功率。

(4)蓄电池运行成本。在蓄电池参与优化调度的过程中，蓄电池的充电和放电均存在一定的损耗，将此损耗考虑到发电侧的运行成本中。

(7)

式(7)中：cbc和cbd分别为蓄电池充、放电的损耗系数；Pbc,t和Pbd,t分别为蓄电池在时段t的充、放电功率。

2.2 约束条件

(1)电负荷平衡约束。为保证系统的供需负荷平衡，需对此设置电负荷平衡约束。

(8)

式(8)中：PL,t为系统在时段t负荷。

(2)机组出力约束。为保证机组能够安全稳定运行，需将机组的出力设置在规定范围之内。

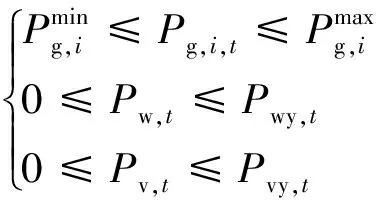
(9)

(10)

(4)系统旋转备用约束。为保证系统安全运行，需设置一定的旋转备用，以应对新能源出力的不确定性和负荷的波动性。

(11)

(5)抽水蓄能机组出力约束。

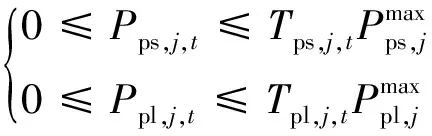
(12)

式(12)中：Tps,j,t和Tpl,j,t分别为抽水蓄能机组j在时段t的发电和抽水启动变量。

执行政府会计制度的单位，是指各级各类国家机关、政党机关、人民团体，以及国家举办的带有公益性质的教育、科技、文化、卫生及从事有关专项公共管理和服务的事业单位。政府会计的“投资”指事业单位在保证正常运转和事业发展的前提下，利用货币资金、实物资产和无形资产向其他单位的投资，其中的货币资金投资指直接以现金、银行存款和其他货币资金作为投入资本进行的投资。

(6)抽水蓄能电站水库库容约束。

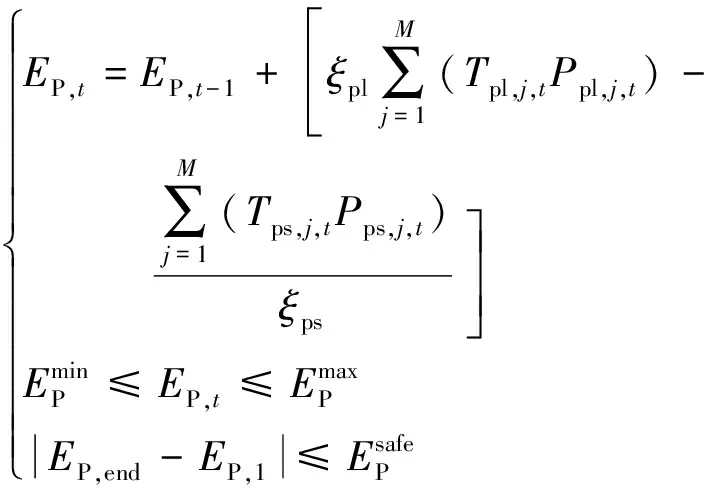
(13)

(7)抽水蓄能机组间的相互约束。根据抽水蓄能电站的整体运行状态和电站中运行的机组数量，对机组间的约束条件加以设置，避免在同一时段中既存在抽水机组又存在发电机组。

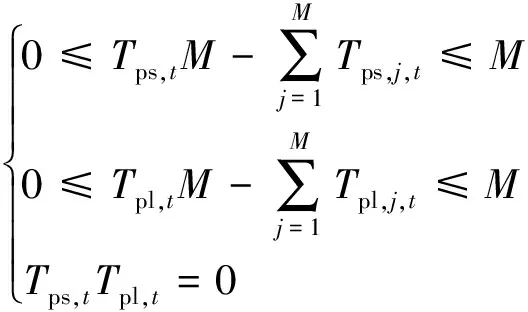
(14)

式(14)中：Tps,t和Tpl,t分别为电站整体在时段t的发电和抽水的启动变量。

(8)抽水蓄能机组最大启动次数限制。为保护抽水蓄能机组，不能对其频繁的状态转换，需对其设置一定的启动次数限制。

(15)

(9)蓄电池出力约束。

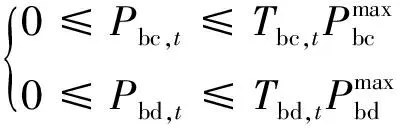
(16)

式(16)中：Tbc,t和Tbd,t分别为蓄电池在时段t充、放电启动变量。

(10)蓄电池容量约束。蓄电池的荷电状态(state of charge，SOC)，反映蓄电池的剩余容量。

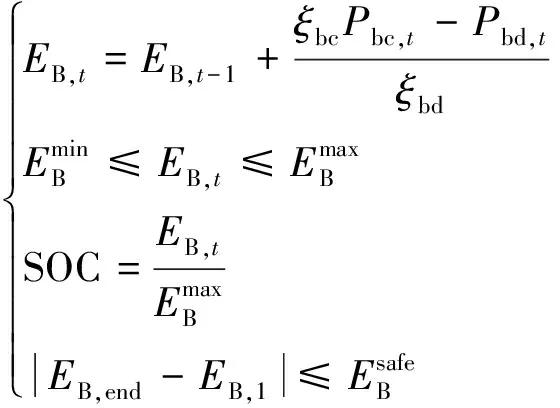
(17)

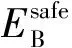
(11)线路潮流约束。

(18)

2.2 模型求解

在完成模型的构建后，为降低模型求解难度，将目标函数中的火电机组的运行成本的二次函数进行线性化处理，共分为K段，描述为混合整数线性规划模型。其中火电机组运行成本分段线性化过程，如图3所示。

图3 火电机组运行成本线性化Fig.3 Linearization of operating costs of thermal power units

根据图3所示，可将火电机组运行成本的函数表达式转化为

(19)

式(19)中：

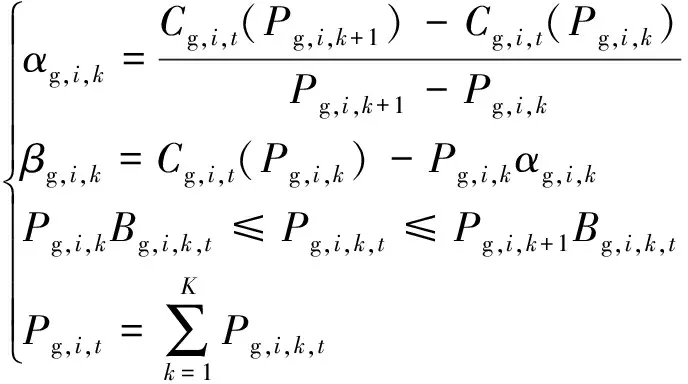
(20)

式中：Cg,i,t为火电机组i在t时段的运行成本；αg,i,k为机组i在第k段分段线的斜率；βg,i,k为机组i在第k段分段线的等效截距；Bg,i,k,t为机组i在t时段第k段分段线的运行状态；Pg,i,k,t机组i在t时段第k段分段线的出力；Pg,i,k和Pg,i,k+1分别为机组i在第k段和第k+1段分段线的出力。

通过上述方法，将模型转化为线性函数，最终在MATLAB中结合YALMIP工具箱的CPLEX商业求解器获得最优解，得到各类电源在预测日的出力情况。

3 算例分析

3.1 算例介绍

采用某地区电网的实际数据作为算例，该地区电网配备6台火电机组、500 MW风电场、300 MW光伏电站、额定容量为45 MW·h的蓄电池，以及含有4台30 MW机组的抽水蓄能电站，其水库最大容量1 000 MW·h。在优化过程中，将水库的可发电量表示为水库容量。其中火电机组的参数，如表1所示。

在进行日前优化调度之前，该地区预测日的负荷以及风电和光伏的出力预测，如图4所示。其中风电的预测出力变化趋势与负荷变化趋势相反，具有一定的反调峰特性。

设置两个不同的优化策略，策略一：储能装置初始时刻与最终时刻容量保持一致；策略二：储能装置初始时刻与最终时刻容量的差值设置安全线。

3.2 结果分析

日前优化调度模型的目标函数为式(3)，约束条件为式(8)～式(18)，对该模型求解后，得到在不同策略下的每个电源不同时刻的出力情况。

表1 火电机组参数Table 1 Parameters of the thermal units

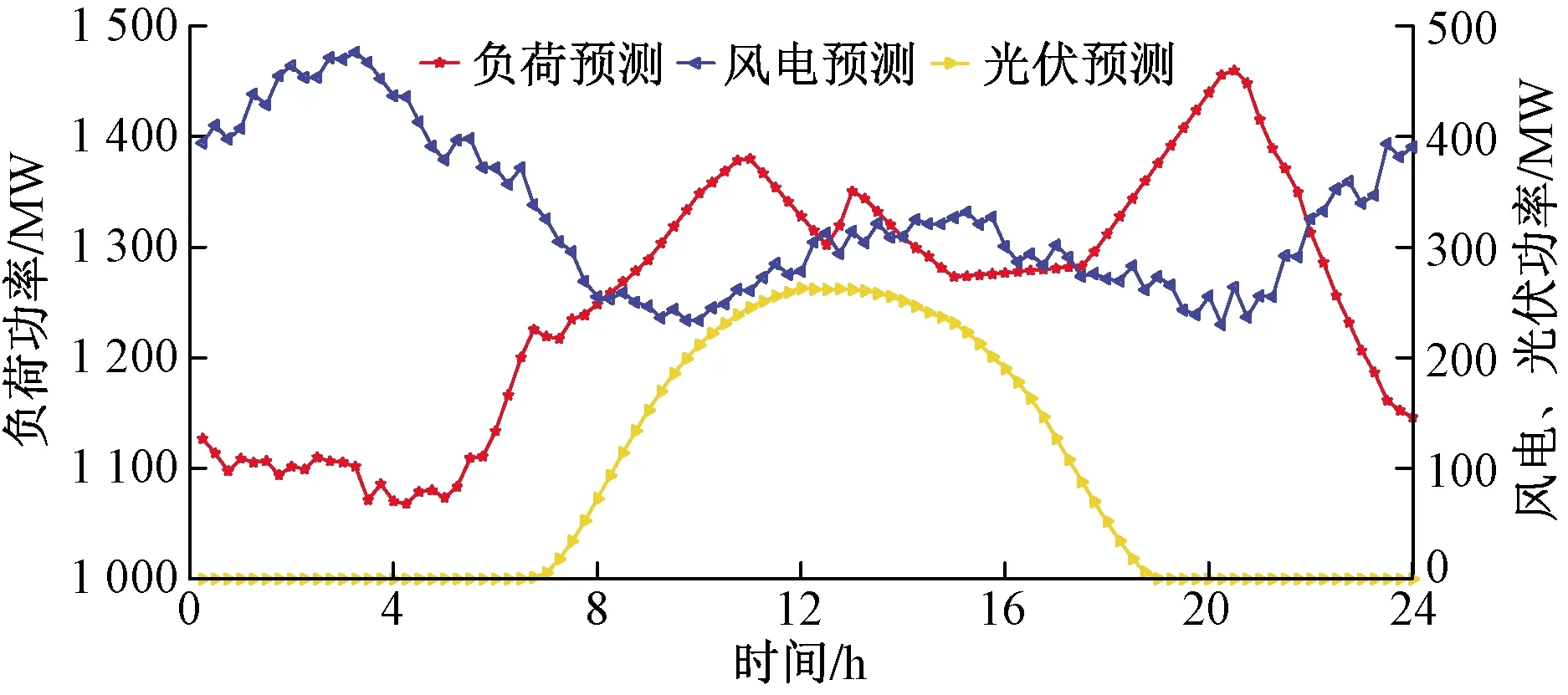
图4 预测负荷、风电及光伏出力Fig.4 Forecast load, wind power and photovoltaic output

根据图3可知，在17:30—21:30时出现用电高峰期。但此时正处于光伏发电截止与风电出力较小时刻，需增加其他类电源出力以满足高额的用电需求。在两种不同策略下火电机组的出力变化情况，如图5所示。晚高峰时策略一和策略二机组出力均增加明显，但策略二的增幅整体低于策略一，机组整体运行压力小于策略一。其余时段在其他种类电源的相互作用下，每台火电机组的出力基本处于稳定状态。这表明，预测日中火电机组的出力不仅受系统负荷的影响，而且受新能源出力变化的影响。

蓄电池参与优化调度时，为延长其使用寿命，设置蓄电池的SOC范围在0.2～0.9。根据模型的求解结果，两种优化策略下蓄电池的荷电状态和出力变化，如图6所示。在两个不同策略下蓄电池的充电和放电时间基本一致。策略一中蓄电池的初始时刻和最终时刻的储能容量均处于0.4。相比策略一，策略二中初始时刻储能容量与策略一相同，但最终时刻的储能容量仅为0.3。即策略二优化能够减少不必要的充电过程，增加蓄电池应用的灵活性，更加贴近实际生产活动。

在模型中对抽水蓄能机组启动成本和运行成本以及水库容量约束进行设置，求解结果中得到策略一和策略二的每台机组出力和水库容量的变化，如图7所示。当前一台机组处于满发或满抽状态时，启用下一台机组，避免过多的启动次数，减少成本。在策略一下，电站中的机组发电启动8次，抽水启动13次；在策略二下，电站中机组发电启动同样为8次，但抽水启动次数较策略一减少1次，为12次。在两个不同的优化策略中，策略一中水库的初始时刻和最终时刻容量均约为600 MW·h，策略二中水库的最终时刻容量约为500 MW·h，相较初始时刻降低100 MW·h，处于水库的安全容量变化范围之内。两种优化策略中，抽水蓄能机组的抽水和发电时间段与蓄电池的充电和放电时间段一致，并且在电站内的同一时段，不存在抽水机组和发电机组共同运行的情况。但两种策略中抽水蓄能机组运行状态的不同之处主要集中于23:00—24:00。为满足水库的最终时刻容量与初始时刻一致的条件，策略一比策略二中的抽水机组多启动一台。相对而言，策略一缺乏一定灵活性，策略二在优化过程中能够加强抽水蓄能机组的实用性。

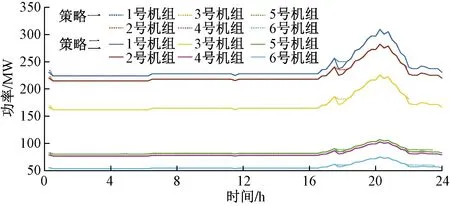
图5 不同优化策略下火电机组出力Fig.5 Thermal power unit output under different optimization strategies

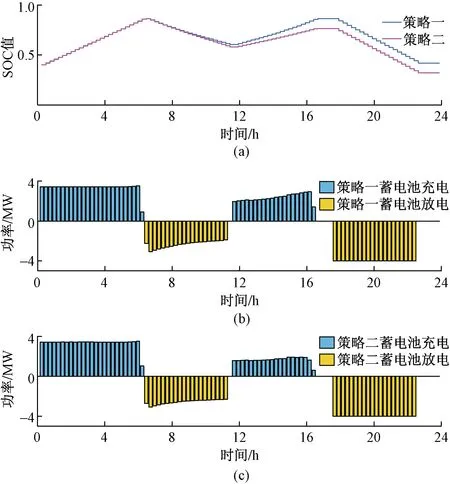
图6 不同优化策略下蓄电池荷电状态和出力Fig.6 Battery state of charge and output under different optimization strategies

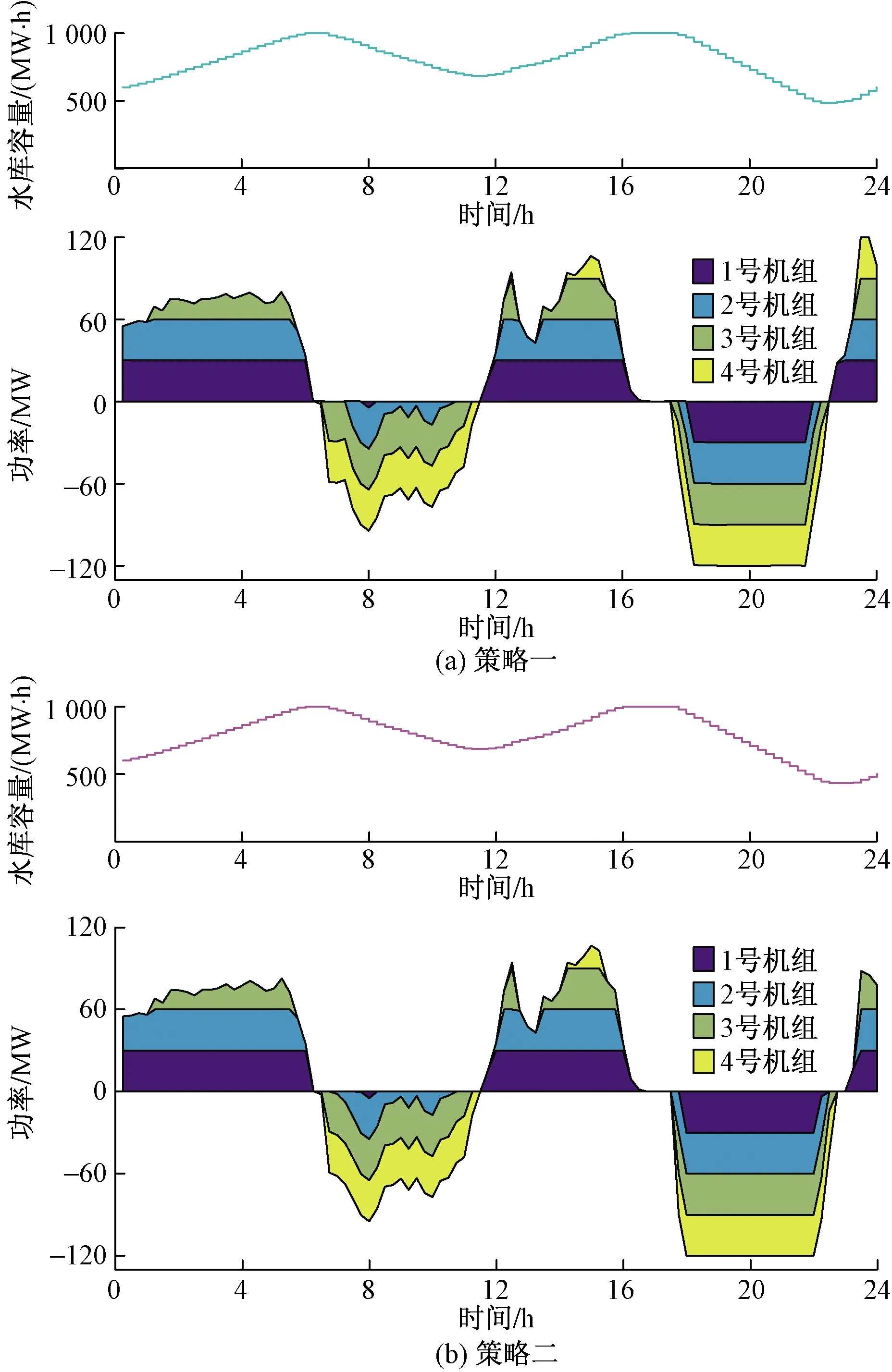
图7 不同优化策略下水库容量和抽水蓄能机组出力Fig.7 Reservoir capacity and pumped storage unit output under different optimization strategies

图8为两种优化策略下水库容量的变化差异。策略一中的水库容量在整个优化过程中均大于策略二下的水库容量，但其变化的差值主要集中在18:00—24:00，并逐渐呈上升状态。两种策略的最终水库容量差值为100 MW·h。

该系统在抽水蓄能和蓄电池的配合下，策略一与策略二弃风电量对比，如图9所示。其中两种优化策略的弃风时段集中于0:00—6:00，在优化过程中策略一的弃风电量为416.85 MW·h，策略二下弃风电量减少为411.29 MW·h。表明策略二不仅能够增加储能装置的灵活性，还可以提高新能源的消纳率。

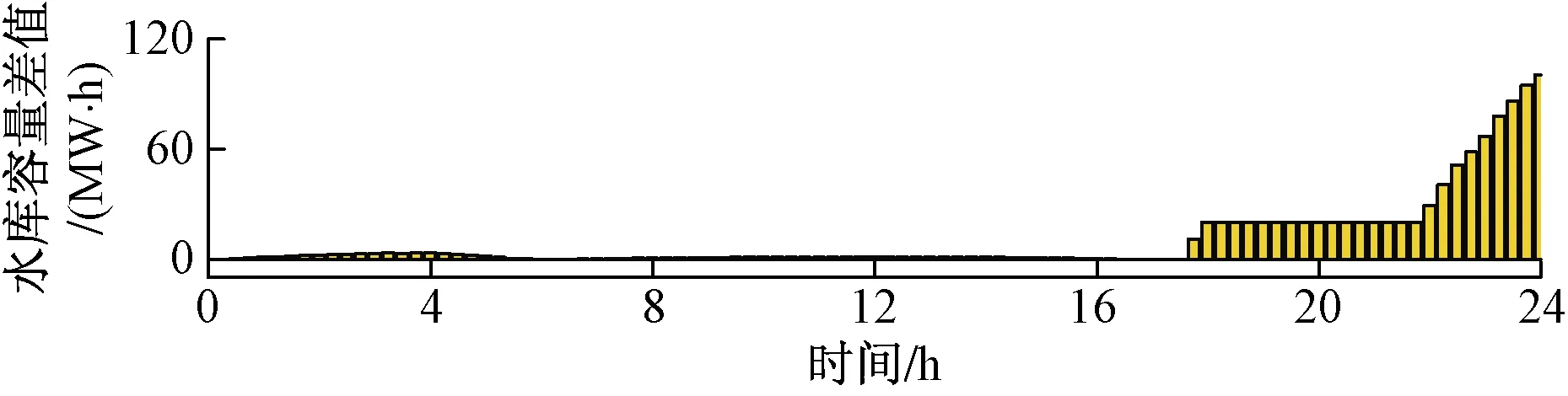
图8 不同优化策略下水库容量差值变化Fig.8 Variation of reservoir capacity difference under different optimization strategies

图9 不同优化策略下的弃风电量Fig.9 Wind power abandonment under different optimization strategies

在利用该模型对预测日的优化调度过程中，最终得到在两种不同优化策略下的各机组及总运行成本，如表2所示。相比策略一，策略二在预测日能够降低总运行成本16 786 元，减少弃电成本2 503 元，其中火电机组的运行成本减少12 640 元。因策略二在安全差值内不限制优化时段中的储能装置初始时刻和最终时刻容量一致，使得抽水蓄能电站和蓄电池内部具有一定的灵活性，能够根据预测日的实际情况及时做出调整。蓄电池的出力变化与抽水蓄能趋于一致，在策略二下储能装置的成本同样也在减少。

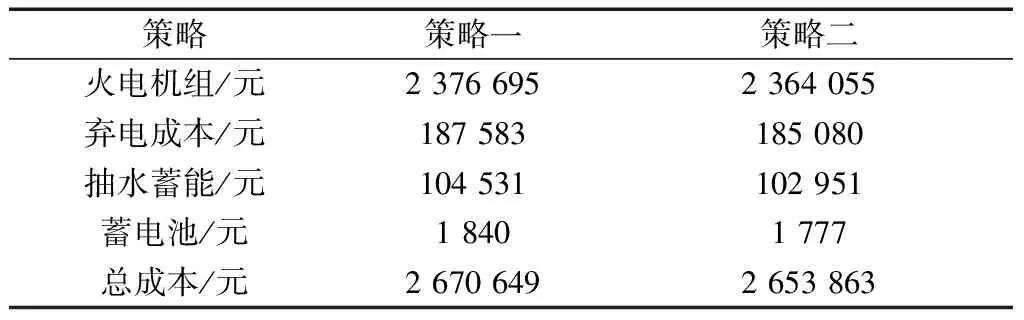
表2 不同优化策略下的运行成本Table 2 Operating costs under different optimization strategies

4 结论

针对新能源出力的随机性和不确定性，为减少弃风、弃光现象，同时提高储能装置在实际调度中的灵活性，将储能装置初始时刻和最终时刻容量一致约束进行改进，设置两时间点的容量安全差值，优化机组运行方式。通过实验结果，得到以下结论。

(1)该优化方式的应用可以协调火-风-光-蓄电池-抽水蓄能之间的关系，合理安排各类机组的出力状态，进一步增加新能源消纳率，减小火电机组压力，从而减少系统整体的运行成本。

(2)与传统储能装置的优化方式比较，该优化方式能够增加储能装置参与电力系统优化调度的灵活性，更大程度地提升储能装置削峰填谷和系统调节的能力，符合实际情况，对实际生产活动具有指导意义。