基于改进下垂法的逆变器并联控制技术

薛阳， 席东翔， 黄薪操， 丁子龙， 陈月钒

(上海电力大学自动化工程学院， 上海 200090)

随着全球变暖等环境问题的日益严峻，全球各国的研究人员将注意力集中到了可再生能源发电上，以减小传统能源发电对环境的污染，与此同时以太阳能和风能等清洁能源为基础的微电网技术取得了重大的突破[1-2]。微电网不仅可以作为整体独立运行，单独储发电供给用户使用，实现区域性的自给自足，而且可以作为大电网的一部分并入电网运行，与大电网之间相互补充，具有极高的实用性[3]。

对逆变器进行有效调节是微电网稳定工作的重要手段，而下垂控制是众多调节方法中最常用的一种[4]。在多逆变器并联系统中，凭借其简单可靠、不用通信而是依照下垂曲线实现功率分配的特点，下垂控制也得到了广泛的应用[5-6]。但是在低压环境下，下垂控制由于线路阻抗差异大、各逆变器特性不一致等因素影响，不易实现输出功率的合理分配[7-9]。为了处理这一难题，文献[10]提出一种旋转坐标功率解耦方法，改进了传统解耦方式，同时提出了下垂限幅的控制方法，改善了下垂控制电压降落情况，但该方法解耦精度较低，动态性能较差。文献[11]加入了随母线电压幅值自适应变化的虚拟阻抗，有效减小了输出电压的大范围波动，但该方法实现阻抗自适应设计较为繁琐。文献[12]改进原有的功率控制策略，新增加了误差纠正环节，提高了功率输出的合理性，但新的控制环过于复杂，实施起来不易实现。文献[13]提出了基于逆变器输出端电压而不是公共连接点处电压的逆变器输出功率计算公式，改善了功率分配情况，环流抑制效果也比较理想。但该方法公式计算较为复杂，实际情况下难以获得计算所需的数据。文献[14]对无功下垂环节进行改进，将原电压控制改为由电压的变化量控制，改善了功率输出的精确性，但该方法电压变化量变化范围较小，对系统精度要求比较高。

针对下垂控制的应用限制以及不同系统参数下的功率分配问题，现首先推出两种电压等级下的逆变器输出功率，然后结合传统下垂的相应问题给出改进措施。最后进行仿真实验，结果显示，本文的改进措施显著改善了传统下垂的问题，实现了各个工况下功率的准确输出，稳定性较好且有一定的动态响应速度，以期为实现逆变器输出功率合理分配提供了理论依据。

1 逆变器并联系统特性分析

1.1 并联系统模型

选择两台同型号的逆变器进行并联处理，其模型如图1所示。

E为电源电压；Zn(n=1,2)分别为两条传输线路阻抗；Un(n=1,2)分别为各台逆变器的输出电压；U0、I0分别为 公共负载Z0的电压和电流图1 逆变器并联系统结构图Fig.1 Structure diagram of inverter parallel system

1.2 并联系统功率特性分析

由图1可以得到系统电路的等效简化图，如图2所示。其中Vn(n=1,2)和δn(n=1,2)分别为逆变器的输出电压幅值和相位，Zn(n=0,1,2)为各线路阻抗的幅值，θn(n=1,2)为各线路阻抗的相位，Rn(n=0,1,2)分别为各线路的电阻，jXn(n=0,1,2)分别为各线路的电感，In(n=0,1,2)分别为各线路流过的电流。

图2 系统主电路等效图Fig.2 Equivalent diagram of the main circuit of the system

由图2可知，公共负载Z0上的复功率Sn为

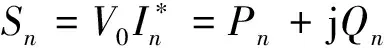
(1)

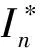
各线路向公共负载输出的电流In为

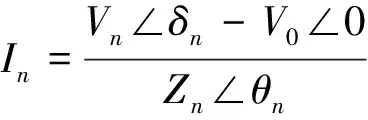
(2)

由式(2)和式(1)可以得到公共负载上的有功和无功功率分别为

(3)

(4)

式中：Rn为线路阻抗；Xn为线路电感。

通常情况下负载阻抗Z0对输出功率的影响比线路阻抗Zn大得多[15]，由此认为δn≈0减小线路阻抗的影响，则有sinδn≈δn，cosδn≈1。由上述理想条件以及式(3)和式(4)可得

(5)

(6)

在低压环境下，系统总阻抗呈阻性，因此式(5)和式(6)分别可以化简为

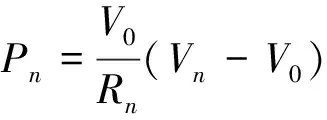
(7)

(8)

在高压环境下，系统总阻抗呈感性，式(5)和式(6)分别可以化简为

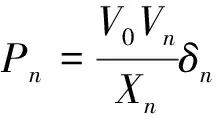
(9)

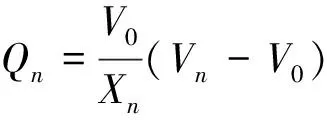
(10)

2 传统下垂控制策略研究

2.1 下垂控制原理分析

由式(9)可知有功功率受多个因素影响，但其中相位差的变化对其结果影响最为显著。又因为各电压相位差δn与角频率ωn有如下关系：

(11)

由此可见，实现对系统频率的有效调节即可最终完成对有功功率的有效调节。由式(10)可知，无功功率同样也受多个变量控制，其中逆变器输出电压的控制效果更为显著。因此，有功功率输出与系统频率、无功功率输出与逆变器输出电压之间满足一定的线性约束关系，再根据发电机特性可以类比推出感性条件下的下垂控制关系为

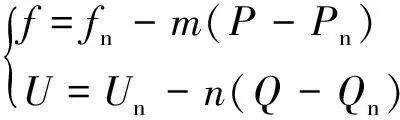
(12)

式(12)中：f、U分别为下垂调节的目标频率和电压；fn、Un分别为额定频率和电压；m、n为P-f和Q-U下垂系数；Pn和P分别为逆变器额定和实际输出有功功率；Qn和Q分别为逆变器额定和实际输出无功功率。

结合以上P-f和Q-U控制方程及f和δn之间的关系可得传统下垂法控制框图，如图3所示。

I为系统电流；Uref为电压合成环节输出的参考电压； 1/s为积分运算环节图3 传统下垂控制框图Fig.3 Block diagram of traditional droop control

2.2 传统下垂控制的局限性分析

传统下垂的问题主要体现在其应用环境限制以及系统参数选取上。

(1)当研究对象为低压微电网时，系统总阻抗为阻性，传统的P-f和Q-U控制在该环境下并不适用。

(2)低压微电网环境下，由于逆变器容量差异、传输线路长度不一致等差异使得并联运行的逆变器难以完成电压的准确输出，无法实现输出功率的合理分配。

(3)传统下垂控制由于P-f和Q-U控制方程下垂系数的选取会对系统动态响应速度以及精确度产生一定的影响，系数过小会导致系统对负载的投切相应不及时，影响输出精度。

3 改进的下垂控制策略研究

对于传统下垂方法中固有的问题,针对性地提出了几点改进方法。

(1)引入虚拟阻抗，使得系统总阻抗等效呈感性，实现P-f和Q-U控制在低电压环境下的成功应用。

(2)增加压降补偿环节,抑制线路阻抗和虚拟阻抗共同造成的电压跌落，使得逆变器输出电压升高，进而实现功率正确输出。

(3)为了保障系统在负载变化时候的动态性能，添加了电压动态反馈环节，该环节还可以和压降补偿一起作用对电压降落起到一定的抑制作用。同时利用微分环节的预测性能，及时对无功功率输出进行修正，进一步提高系统的动态性能。又因为功率不能精分主要原因在于逆变器输出无功功率的误差，故在无功下垂中添加积分环节，抑制电压变化对无功功率的影响。

3.1 虚拟阻抗环节

虚拟阻抗环节工作原理如图4所示。

Zv为虚拟阻抗；为新电压参考值图4 虚拟阻抗法控制框图Fig.4 Control diagram of virtual impedance method

为了简化计算，虚拟阻抗Zv为纯感性，但是添加额外阻抗会进一步导致系统电压产生降落，并且电压降落值与虚拟阻抗增加值成正比，由此可见，在使系统总阻抗呈感性的前提下，虚拟阻抗应越小越好以减小电压降落。

在逆变器满足电压幅值在系统电压附近和按规定容量之比进行无功功率输出的两个条件下，对虚拟阻抗进行了取值验证，并规定逆变器1和逆变器2的容量之比为2∶1。最终选定虚拟阻抗值为0.55 mH，两个约束条件对应的输出情况如图5所示。

图5 Zv=0.55 mH逆变器输出电压和无功功率Fig.5 Inverter output voltage and inverter output reactive power when Zv=0.55 mH

由仿真结果可知，在虚拟阻抗取0.55 mH时系统电压和逆变器输出无功功率满足约束条件。

3.2 压降补偿环节

并联运行的各逆变器在正常工作时，由于存在积分环节，其电压频率相同，各台逆变器的相角差很小，有功功率理论上能够完成合理输出[16]。但是，各传输线路线路阻抗不一致导致的电压幅值跌落不同会引起无功功率无法合理输出，通过在下垂控制环节中添加电压降落补偿项Ud并通过正反馈的方式加入系统额定电压上，等效增加各逆变器输出电压，从而实现并联线路在连接点处电压幅值相等，最终实现各自无功功率的合理输出，其中电压补偿项Ud的计算公式为

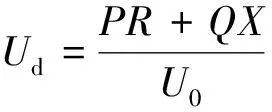
(13)

式(13)中：R和X为线路电阻和电感；P和Q为逆变器实际输出有功和无功功率；U0为公共节点处电压。

3.3 电压动态反馈环节及微分积分环节

系统在投入新的负载时，负载电压会产生一定的降落，进而会影响电压合成环节的参考电压，传统下垂控制无法迅速对负载的变化做出响应，通过在无功下垂中加入电压动态反馈环节可以提升系统对负载变化的响应速度。其中动态反馈环节由逆变器输入电压和公共负载处电压的差再乘以一定的反馈系数然后加到额定电压上，从而使得负载电压的变化及时反馈到无功下垂控制环节中，获得一个较为稳定的参考电压。该环节在对负载变化反应迅速的同时还可以对压降起到一定的抑制作用，提升功率输出的合理性。同时充分利用微分环节dQ/dt的预测性能，及时对无功功率与额定无功功率误差进行修正，进一步提高系统的动态性能。

通过在无功下垂中添加积分环节1/s提升各逆变器功率输出的准确度。积分环节进一步减轻各条线路阻抗不一致等对输出功率的影响，实现逆变器有功和无功功率更为合理的输出。

综合以上几点改进措施可得改进的下垂控制框图如图6所示。

U0为公共负载处电压；k为电压动态反馈环节的控制系数图6 改进下垂控制框图Fig.6 Block diagram of improved droop control

4 仿真结果及分析

在MATLAB/Simulink平台下搭建低压微电网下两台逆变器并联系统仿真模型。仿真电源采用直流电源模型，系统运行时间为0.6 s，并且在0.3 s时增加公共负载。

为了检验本文所提改进策略的可行性，进行了4组仿真实验，4种工况均以功率合理输出为目标，以此为前提在逆变器容量和线路阻抗的变化约束中对比传统下垂和改进下垂的有效性。其中，工况一、工况三使用传统下垂方法，工况二、工况四使用改进下垂方法，仿真模型使用的具体参数如表1所示。各工况下线路以及逆变器参数如表2所示。4种工况下，两台逆变器在两段仿真时间内的输出功率具体数值如表3所示。

(1)工况一。图7为工况一时的仿真波形图，两台逆变器容量相同但是线路阻抗比不一样时，逆变器有功功率在短时间的波动之后实现按容量比进行合理输出，但是对投入负载时响应较慢。而各逆变器无功功率产生了较大波动，功率分配与容量之比相差较大，而且对负载的投入反应不灵敏。

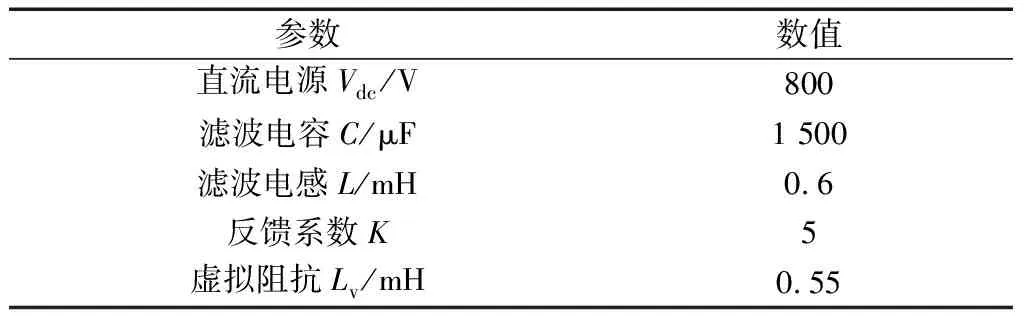
表1 仿真模型参数Table 1 Parameters of simulation model

表2 逆变器参数Table 2 Parameters of the inverter

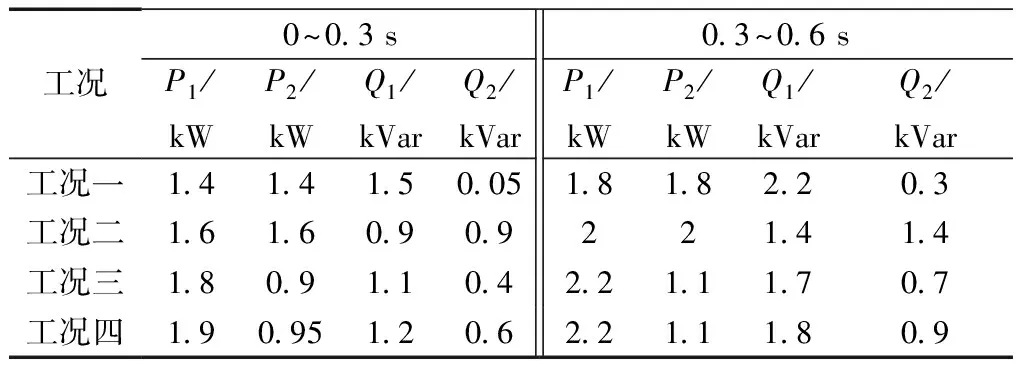
表3 逆变器输出功率Table 3 Inverter output power

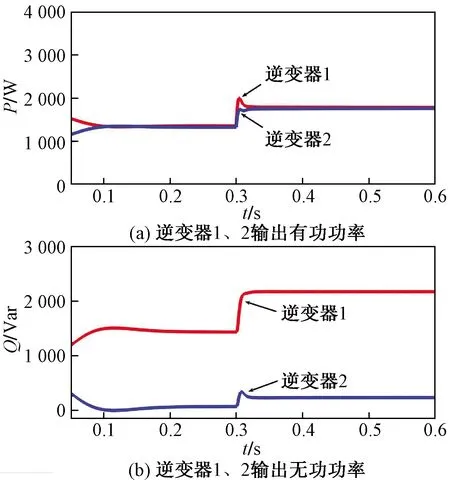
图7 工况一仿真结果Fig.7 Simulation result of case1

(2)工况二。两台逆变器除都使用改进下垂策略外，其他参数与工况一保持一致。图8为工况二时的仿真结果图，在改进下垂方法下，当线路阻抗比与逆变器容量比不一致时，有功和无功功率都能做到按照规定容量比进行合理稳定输出。而且在系统增加公共负载的情况下继续保持输出功率合理分配，同时系统对负载的添加响应迅速，过渡平滑。

(3)工况三。两台逆变器都工作在传统下垂方法下。图9为工况三时的仿真波形图，当两台逆变器容量不相同时，系统有功功率虽然能实现合理输出，但是对负载的投入响应较慢；同时在传统下垂控制下无功功率仍不能做到合理输出，且出现较大误差，功率输出稳定性较差，出现较大波动。

(4)工况四。两台逆变器均在改进下垂方式下工作，其他参数与工况三相同。图10为工况四时的仿真结果图，当逆变器的容量不同且线路阻抗比与容量比不一致时，在改进下垂方法控制下，有功和无功功率均能实现按容量比合理稳定输出，且对公共负载的投入响应及时，反应迅速。

图11为仿真过程中两种控制策略下的系统母线处电压波形对比图。在传统下垂控制策略下，系统母线电压幅值为297 V，较预设电压幅值有明显的下降。而在改进下垂控制下，系统母线电压幅值约为309 V，可以做到维持在额定电压附近，保证了系统电能质量的可靠。

图8 工况二仿真结果Fig.8 Simulation result of case2

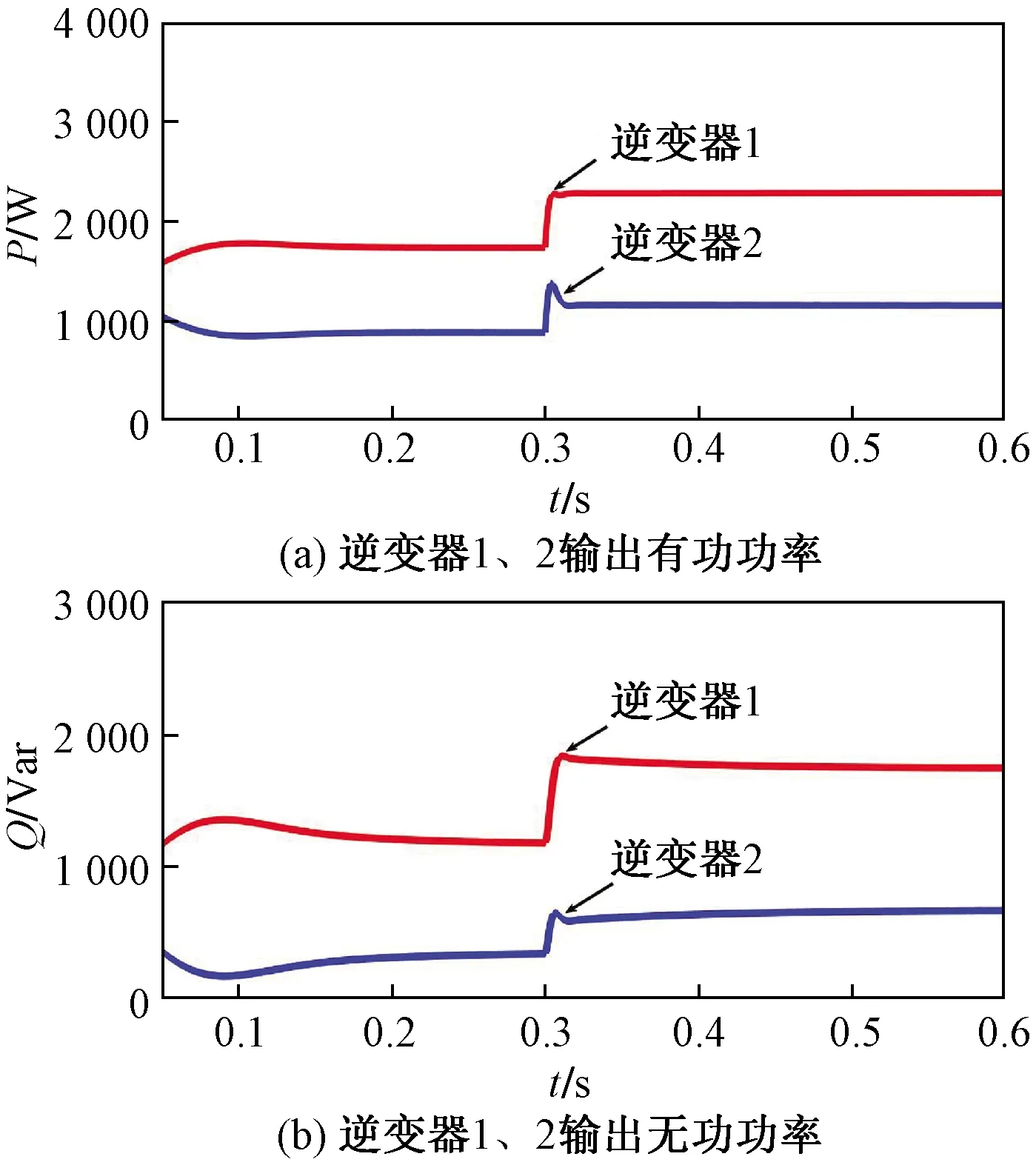
图9 工况三仿真结果Fig.9 Simulation result of case3

图10 工况四仿真结果Fig.10 Simulation result of case4

图12为仿真过程中两种控制策略下的系统环流对比图。在传统下垂控制下，系统环流幅值较大约为2 A。而在改进下垂控制策略下，系统环流幅值减小到0.8 A，有助于并联系统正常可靠运行。

综合上述各工况下仿真结果可得，当线路阻抗比与逆变器容量比不一致时，在传统下垂策略下，系统有功功率虽然可以实现合理输出，但是逆变器能够稳定输出所用时间较长且对负载的投入响应不够迅速；同在传统下垂策略下，无功功率无法实现合理输出，且产生波动及发生较大输出误差，稳定性较差。在本文提出的改进策略下，逆变器输出有功功率和无功功率都能够完成合理输出，且稳定输出用时较短，无较大波动，对负载投入响应迅速。同时，在改进下垂策略下，母线电压降落及系统环流都得到明显抑制，系统运行可靠性得以提升。

图11 母线电压对比图Fig.11 Comparison diagram of bus voltage

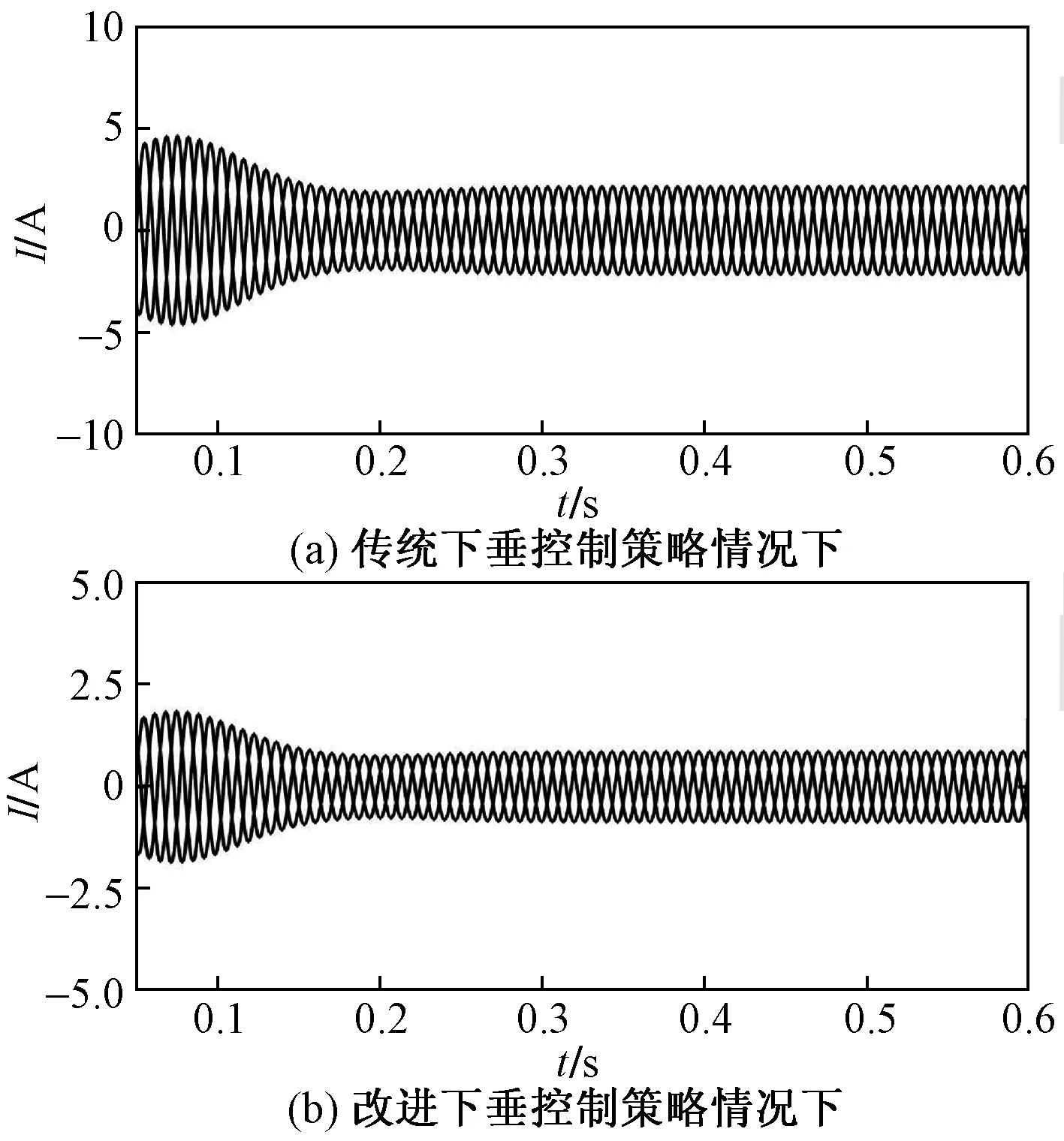
图12 系统环流对比图Fig.12 Comparison diagram of circulation

5 结论

为了更好地在低压逆变器并联系统环境下应用传统下垂方法，首先通过添加最佳虚拟阻抗解决了传统下垂方法的应用局限性问题。然后提出改进的下垂控制策略，将积分环节和微分环节引入到无功电压下垂控制环节，并且在额定电压基础上添加了电压补偿项以及电压动态反馈环节。通过仿真分析得出，该改进策略不仅实现了逆变器有功功率和无功功率的合理输出，而且提升了系统的输出稳定性及动态响应速度，还有效地抑制了母线电压降落和系统环流,验证了所提策略的合理性和有效性。