基于单层小波变换的视觉传感图像超分辨率重建*

张 剑刘 鑫

(1.山西职业技术学院计算机工程系，山西 太原 030006；2.中南大学计算机学院，湖南 长沙 410083)

近年来，随着前沿技术的发展，使得视觉图像成为获取数据信息的直接途径，并在军事、医疗、治安以及工业等各个领域都取得了重要应用。但由于技术的不成熟或外界环境因素的影响，在视觉成像的过程中，会因为图像的分辨率过低而增强边缘细节刻画的模糊性，进而影响整体的清晰度。所以就需要根据实际情况，采用相关技术手段对分辨率异常的问题实现有效解决。而基于视觉传感图像的超分辨率重建策略，采用目标插值等技术手段成为现阶段的主要解决方法之一，该方法可以保存更多的细节以及高频信息，且算法的鲁棒性和实用性较强，是目前传感领域的研究热点及重点。

文献[1]提出一种基于卷积神经网络的传感视觉图像重建方法，主要通过卷积神经网络建立三维通道对图像进行输入传输，提取分辨率较低的信息数据，进行图像的超分辨率重建。该方法技术要求较高、算法实施难度过大、整体实用性较差；文献[2]则是通过深度学习方法来识别图像的超分辨率，利用自相似算法实现图像细节的转换。该方法对细节控制效果较差，且忽略边缘位置的模糊度量问题，导致图像出现失真现象；文献[3]将稀疏表示应用于图像超分辨率重建，利用亚像素精度的配准和自适应加权特征算子，从多个含噪的低分辨率像素中重建高分辨率像素。但是，该方法的鲁棒性问题尚未得到有效解决；文献[4]通过特征映射注意机制提取低分辨率图像中的可用特征，并将多个特征进行融合处理。通过调整图像信息特征，完成图像的超分辨率重建。但是，该方法的整体耗时过长，导致重建效率不足。

综合上述出现的问题，本文主要通过空间感知方法来改善视觉传感图像的分辨效果，并利用单层小波变换的特征优势去除图像中的干扰噪声，这样对图像尺度的细节分析会更加直观便利。

1 基于单层小波变换的图像去噪预处理

由于外界信号传输环境的影响，视觉图像受外部因素干扰，其中信道噪声对成像的干扰尤为严重，所以需要针对噪声问题对原始图像进行预处理操作，去除异常信息。为了提高去噪的可靠性，采用单层小波变换算法进行去噪处理。

设含有信道噪声数据的图像为v(i)；待重建且未受到异常数据干扰的图像为u(i)；n(i)表示分辨率均值为0的信道噪声(多为高斯白噪声)数据；将三者结合得到此关系式v(i)＝u(i)＋n(i)，并且该关系式符合高斯分布条件，根据欧式距离[5]公式对此进行具体表达为:

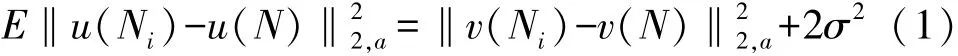
式中:σ2表示方差均值；a为常数值，表示高斯白噪声标准差，对于样本像素点k，设定一个形状为矩形的邻域范围表示为N k，在该范围内对图像中任意像素点i和j之间的欧式距离进行加权计算，表达式为其中E表示欧氏距离参考阈值，且高斯白噪声的标准差值范围为[0.01，0.4]。由此可知，在该关系式中受噪声数据影响的视觉图像加权距离的平方差、与正常图像的方差值为常数2σ2，基于此，就可得出任意像素i与j之间目标相似度的加权值，表达式为:

式中:w(i，j)表示控制加权值；z(i)表示噪声调整函数，表达式为:

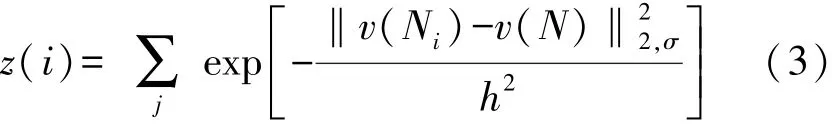
式中:h表示图像平滑参数[6]，式(3)可表达为是归一化后的计算结果。基于上述过程，就能通过调整参数h对原始图像的噪声位移进行调整计算。并根据控制权值w(i，j)的数值大小，使其满足该条件0≤w(i，j)≤1且∑w(i，j)＝1，借此实现降低噪声、改善图像平滑度的目的。

2 边缘多特征性分辨率检测

为保证图像细节的特征效果，根据多尺度结构特征[7]对图像中处于边缘微值的分辨率进行具体检测，基于高斯平滑[8]ξ(x，y)定义小波变换函数为

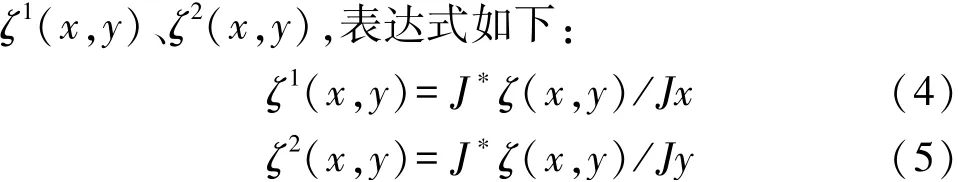
式中:J*表示边缘保持特征[9]平滑位移参数；设:

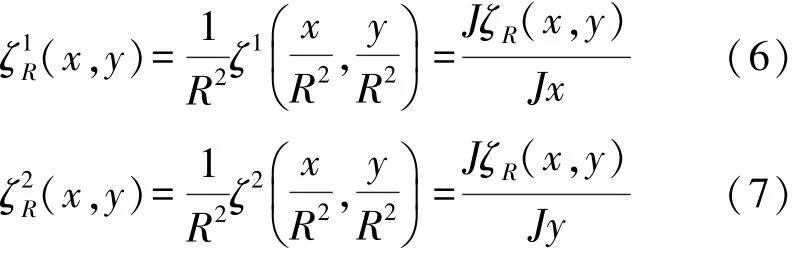
式中:R2表示尺度标量参数，图像在进行边缘检测[10]时在x和y方向上的变化分量以及模糊度量表示为:

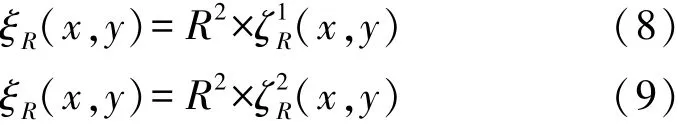
根据上述过程中计算的变化分量及模糊度量值，就可准确检测处于图像边缘[11]位置的分辨率数值。边缘分辨率检测流程如图1所示。

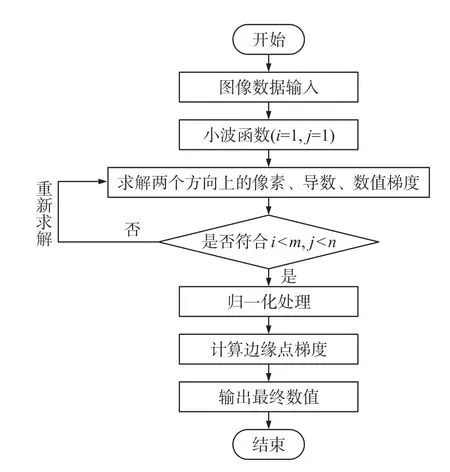
图1 边缘分辨率检测流程

3 图像超分辨率重建方法

以上述经过计算处理后的图像数据为基础，设定一个大小为L×L的灰度图像[12]表示为f(x，y)，假设该图像内正常像素分布的数值关系为L＝2n(n取正整数)。在分辨率较高的视觉传感空间V n内，对灰度图像f(x，y)实行单层小波变换[13]，将原始图像按照降序关系依次进行排列组合后，再分布到分辨率较低的视觉传感空间V0内，并且V0的基底层中只存在一个单一元素为φ0，0，其他层次的元素展开系数为λ0，0，基于此对f(x，y)进行展开计算:

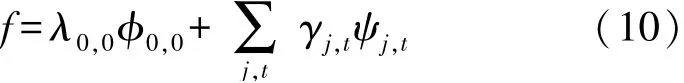
式中:γj，t和分别ψj，t表示在像素j和时间t下的参考系数，得出以下关系式:

式中:γj，t(0≤j≤n)，对参考系数γj，t和ψj，t采用Huffman树方法进行数据编码，将编码后的图像系数按照顺序整理为集合。在该集合中先写入灰度图像f(x，y)在分辨率较低的空间V0内的展开系数为λ0，0；在分辨率较高的空间V n内的展开系数为φ0，0。再写入小波变换[14]空间W t内任意三点展开系数为γ1，t、γ2，t、γ3，t，以此类推，直至按照参数要求写完全部的展开系数γj，t。将全部系数进行小波逆转换，就可得到接收方的最低分辨率的重建图像表达为:

式(12)为原始灰度图像f(x，y)在分辨率较低的空间内的具体表现。

以上述过程为依据，对灰度图像f(x，y)在小波变换空间内的展开系数γ1，t、γ2，t、γ3，t进行逆转换操作，得出以下关系式:

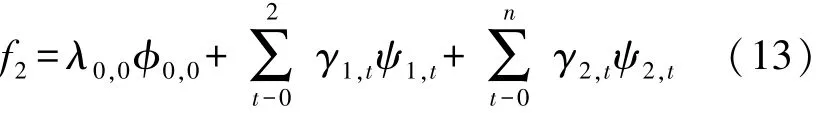
通过以上过程，就能根据像素点的分辨率高低对应进行小波转换及逆转换，至此完成视觉传感图像的合理重建。视觉传感图像的超分辨率重建过程如图2所示。

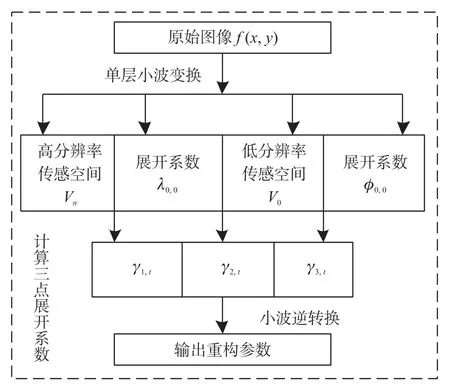
图2 超分辨率重建过程

4 仿真实验

4.1 实验设置

为保证仿真实验的真实性及准确性，本文测试过程主要在MATLAB平台上进行，数据编译软件采用的是Math Works微软公司出品的MATLAB 2019款商业数学软件，用于原始图像处理及视觉信息计算等工作。

以256×256的视觉传感图像为实验对象，进行具体超分辨率重建测试。在对原始图像的分辨率数据进行获取时，为确保像素信息的清晰度及时效性，将分辨率重建的平均倍数取值为2。

本文将从主观以及客观的辩证角度上，分析参考文献[2]提出的深度学习图像重建法、参考文献[3]提出的稀疏表示图像重建法与本文方法对原始图像的重建效果，保证实验的真实性和可行性。主观的分析角度就是对比三种方法下的重建图像，在正常亮度环境下其曝光率、清晰度以及细节内容的具体表现；

而客观的分析角度就是对比三种方法的SSIM(结构相似性)以及PSNR(峰值信噪比)的具体表现。其中，SSIM的是0～1之间的数值，数值越高表明该方法对原始图像细节的保留性越好，反之则越差；PSNR的数值越高表明图像噪声数据的处理效果越好、清晰度越高。

PSNR的计算公式为:

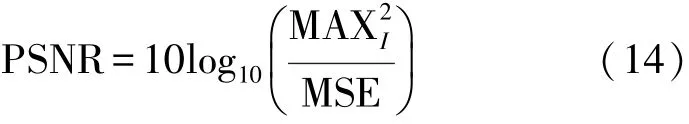
式中:MSE表示误差方根；MAXI表示图像像素的最大值。

SSIM的计算公式为:

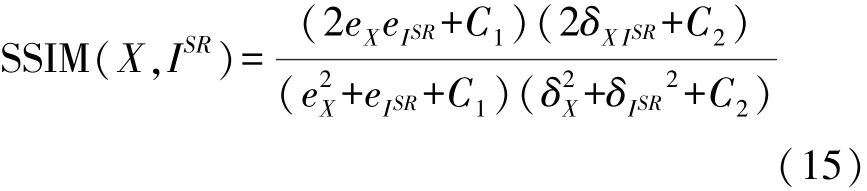
式中:e X、e I SR为原始图像和重建图像的像素均值；C1和C2为常数值。原始图像方差为重建图像方差为δI SR

2；δX I SR为协方差。

4.2 视觉重建效果对比分析

选取40×40像素，且大小为256×256的图像为原始图像，完成超分辨率的重建，效果对比如图3所示。

图3 超分辨率重建对比结果

从图3中可以看出，原始图像3(a)属于低分辨率图像，整体色调不清晰、在局部视野中细节特征出现模糊现象。

观察图像3(b)稀疏表示法重建后的视觉效果，与原始图像相比，清晰度有所提高但分辨率还是较低，对于细节纹理的刻画效果较差，出现了特征丢失及视觉伪影现象，并且局部视野中的效果也不是很理想，物体边缘位置失真现象严重，说明重建算法没有对噪声数据以及低分辨率的影响实现有效解决。

而图像3(c)深度学习图像重建法也出现了同样的状况，齿距现象严重且出现大量噪声点，影响整体图像的视觉观感，清晰度及分辨率都较低，边缘位置有明显的模糊现象。出现这种现象的主要原因就是，该方法没有对原始数据进行降噪处理，导致出现大量高斯白噪声分布点使得细节特征丢失、影响图像的重建效果、降低分辨率以及清晰度。

反观图像3(d)本文方法重建后的视觉图像，与原始图像相比不仅保留了原始的特征信息，还实现了深度刻画，提高了视觉观感性。通过局部视野的细节观察可以看出，对于细节的纹理特征以及边缘位置的噪声处理效果较好，没有出现任何视觉伪影及图像失真现象。这主要是因为，本文方法采用单层小波变换算法针对区域噪声进行了预处理，在不破坏原始特征数据的前提下，提取了深层次的细节信息，在最大程度上改善了边缘模糊及色调不明现象。

4.3 信噪比及结构相似性参数对比分析

随机抽取数据库内1 000张待重建图像，分别使用三种方法在10 h内完成图像重建工作，同时计算每小时内重建后图像PSNR及SSIM均值，结果如图4、图5所示。

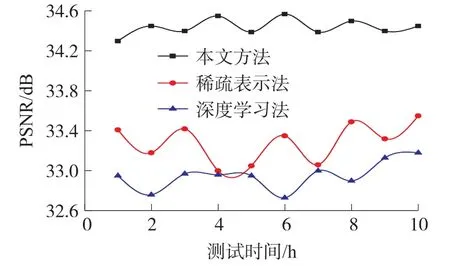
图4 三种方法的信噪比对比

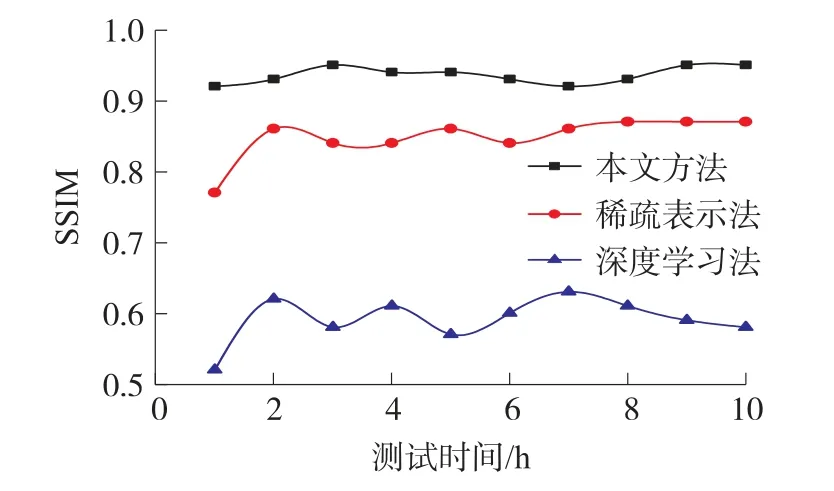
图5 三种方法的结构相似性对比

从图4中可以看出，深度学习法和稀疏表示法的信噪比数值曲线呈较大幅度波动趋势、数值变化较为严重。这说明二者方法的重建效果不理想，受噪声影响严重，导致峰值信噪比较低且不断变化，稀疏表示方法与深度学习方法的最高信噪比分别为33.55 dB与33.18 dB。出现这种现象主要是因为:在计算的过程中忽略了高低分辨率空间关系，没有对原始图像的分辨率参数进行细节划分，导致出现数据混杂的现象，增加重建误差。

而本文方法的峰值信噪比曲线分布范围较小，整体走势相对较为平缓。信噪比数值是衡量图像失真问题的重要标准，本文的信噪比是所有方法中最高的，最高值达到34.57 dB，最低值为34.3 dB，最低值也高于两种对比方法，这说明本文方法的重建效果较好，对过程中出现的信道噪声问题实现了合理解决，去除了干扰现象。

从图5中曲线的增长趋势变化，可以直观地反映出三种方法对视觉图像超分辨率的重建效果，其中，本文方法的相似度数值呈略微波动的增长趋势，最后稳定在一个数值，本文方法的结构相似性参数变化范围为0.92～0.95。说明本文方法对原始图像的信息保留效果较好，没有出现结构破坏现象，这也在一定程度上表明了本文重建算法的优异性。而对于另外两种方法的结构相似性变化曲线，整体处于较低的数值水平，稀疏表示法的结构相似性变化范围为0.77～0.87，深度学习方法的结构相似性变化范围为0.52～0.63。说明两种对比方法重建后的图像与原始图像特征差异性较大，对特征细节的保留效果较差，算法的性能水平较低。

5 结论

本文研究视觉传感领域图像的变换特征，并加以分析给出基于单层小波变换的超分辨率重构方法，利用算法特点来提升图像质量，并使用目标像素加权的预处理手段实现信道噪声的提升，减少计算误差、提高图像重建质量。针对图像的细节特征模糊问题，也通过空间分级操作实现有效改善。本文算法在保证图像高频信息的同时还能有效解决高斯噪声问题，与原始图像的相似度较高，最高PSNR与SSIM分别为34.57 dB与0.95 dB。

由于人眼对图像的曝光度及亮度变化较为敏感，所以，基于超分辨率的重建方法只适用于高亮度的像素通道，针对此问题，如何有效改善重建方法的局限性是下一步的研究重点。