基于DCNN的无人直升机自转过程建模
傅春啸,屈天祥,滕 飞,盛守照
(南京航空航天大学自动化学院,江苏 南京 210016)
0 引言
直升机自转着陆是在直升机动力失效后实现直升机安全着陆的唯一手段,由此,研究无人直升机自转降落对于直升机安全具有重大意义。
研究无人直升机自转状态下的动力学建模是分析和控制该过程的基础,建模的精度直接决定了飞行控制的鲁棒性和准确性。目前主流的对小型飞行器自转过程建模主要采用第一性原理建模、系统辨识建模以及两者结合的方法[1-3]。
孙涛等[4]为直升机建立了13阶线性模型,并从扫频数据中学习模型参数;Lai[5]提出了利用神经网络(NNs)来辨识未知的惯性矩阵,从而在线补偿气动力;Abbeel[6]采用灰箱法建立了直升机自转着陆动力学模型;Setu等[7]在时域上对基于第一性原理推导的直升机加速度预测模型进行了辨识。
由于深度卷积神经网络(DCNN)在高维状态空间中对状态相关性的提取表现出极好的性能[8-9],因此本文在加速度预测模型的基础上添加了DCNN补偿项。通过该补偿项,模型可以从连续的飞行数据中学习到下一时刻隐藏状态的固有表达形式,从而更好地描述飞行过程中各个状态量,提高了模型的精度。本文的改进主要包含2个方面:
a.将DCNN补偿项引入直升机自转过程的动力学建模。
b.提出了利用连续的时间序列状态训练直升机自转着陆模型,在动态建模中表现出很高的准确性。
1 无人直升机自转建模
本节将具体介绍基于DCNN的无人直升机自转过程的动态建模方法。它实际上是一个基于第一性原理的加速度预测模型和一个8层深度的卷积神经网络的组合。加速度预测模型代表了动态模型的确定性部分,而DCNN项则描述了系统动力学中隐藏状态。
1.1 模型结构
无人直升机自转状态下的加速度预测模型由速度、角速度和主旋翼速度七维状态组成。模型减去惯性和重力的影响,得到机体坐标系下的加速度,具体的模型形式为
(1)
u,v,w为机体系下的三轴线速度分别表示前向速度、侧向速度以及垂向速度;p,q,r为机体系下的三轴角速度;gu,gv,gw为机体系下的重力分量;Ω为主旋翼转速;Jx,Jy,Jz为三轴转动惯性;τlat为横向周期变距,它使直升机产生滚转操作;τlon为纵向周期变距,它使直升机产生滚转操作;τped为尾桨(方向舵)控制,它影响尾桨推力,并可用于使直升机偏航(转弯);τcol为主旋翼总桨距控制,通过改变旋翼桨叶的桨距来改变主旋翼推力;U0,Uu为前向速度通道待辨识参数;V0,Vv为侧向速度通道待辨识参数;Ww,Wcol,WwO,W0为垂向速度通道待辨识参数;Pp,P0为俯仰通道待辨识参数;Qq,Q0,Qlon为滚转通道待辨识参数;Rr,R0,Rped为偏航通道待辨识参数;OΩ,O0,Ocol,Ow为转速通道待辨识参数。
加速度预测模型具有辨识参数少,结构简单的优点,但其无法刻画实际飞行状况下的隐藏状态(如抖动等)。因此在加速度预测模型的基础上增加了DCNN补偿项,用来描述隐藏状态,形式为
(2)
Δ项为飞行过程中的隐藏状态即由于气流以及直升机的抖动等引起的建模误差,该项将由DCNN网络通过实际飞行数据来进行学习。
1.2 深度卷积神经网络结构
本文所用到的卷积神经网络如图1所示,它由8层(1个输入层、2个卷积层、2个汇集层和3个内积层)组成。为了简明描述,卷积层是Convγ表示,池化层用Poolγ表示,全连接层用FC-ζ表示。其中γ为层号,ζ为神经元个数。深度卷积神经网络具体结构参数如表1所示。

表1 深度卷积神经网络结构参数
Conv1中包含32个Feature Map,包含800个可训练参数以及294 400个连接;Pool1中包含32个Feature Map,包含144个可训练参数以及12 672个连接;Conv2中包含64个Feature Map,包含1 600个可训练参数以及140 800个连接; Pool2中包含32个Feature Map,包含128个可训练参数以及2 560个连接。卷积神经网络的激活函数f选取为线性ReLU函数。

图1 深度卷积模型
(3)

于是深度卷积神经网络的输入为一个H×18列的矩阵。每一行是一个时刻的所有状态信息,每一列是一个状态在H个相邻时刻下的值。根据Taken定理[10-11],如果H足够大,那么直升机在自转着陆过程中的整个隐藏状态项可以用Pt表示。假设具有相似动力学行为的2条轨迹也将具有相似的隐藏状态,从而具有相似的系统动力学,因此本文利用DCNN补偿项,从具有相似飞行行为的训练样本中学习到隐藏状态的固有表达形式,并通过测试样本验证所提出模型的精度。
1.3 模型参数计算方法
对于本文提出的基于深度卷积神经网络的直升机自转着陆模型,通过二步法确认模型中的未知参数。首先假定卷积补偿项为0,通过最小二乘法确定加速度预测模型中的模型参数,然后固定这些确定参数,通过随机梯度下降算法优化DCNN的参数,采用以下所示最小化函数:
(4)
ζ为深度卷积神经网络;η为神经网路参数;Δ(s,η)为式(2)中所有不确定项部分。于是式 (4)中的优化可以分解为7个子问题,包括3个线速度不确定项,3个角速度不确定项,以及1个转速不确定项。
2 模型训练
试验使用了一架质量为5.1 kg的Align760直升机,主桨叶长度为760 mm。由于原始传感器数据具有较大的噪声,实际记录下来的飞行数据经过了卡尔曼滤波处理,采样频率为50 Hz。考虑到地效对直升机飞行带来的扰动,截取离地2 m以上的飞行数据作为有效飞行数据进行试验。本文将记录数据的70%作为训练集,其他的被用作测试集。
对于模型中的非DCNN项参数,本文先将DCNN补偿项置为0,然后简单求解一个线性最小二乘问题来获得动态模型中的参数,求解的参数结果如表2所示。
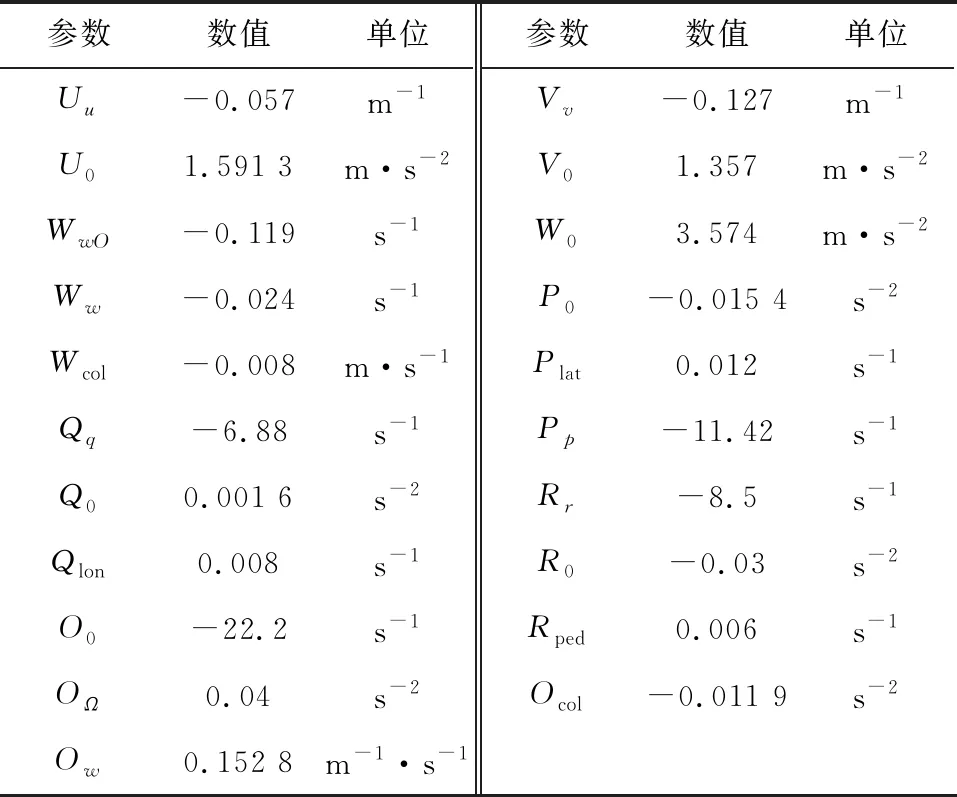
表2 辨识模型参数
对于模型中的DCNN项参数,本文使用梯度下降算法对深度卷积神经网络中的参数进行优化。为了提高优化速率对采集数据进行归一化处理以及统一度量单位处理。
3 模型精度验证
为了验证所提出的DCNN补偿模型的精度,本文利用了在不同高度条件下进行自转着陆的数据,来对DCNN补偿模型与加速度预测模型的预测精度进行比较。在60 m高度悬停条件下进行自转着陆的对比结果如图2~图6所示。

图2 垂向速度对比曲线
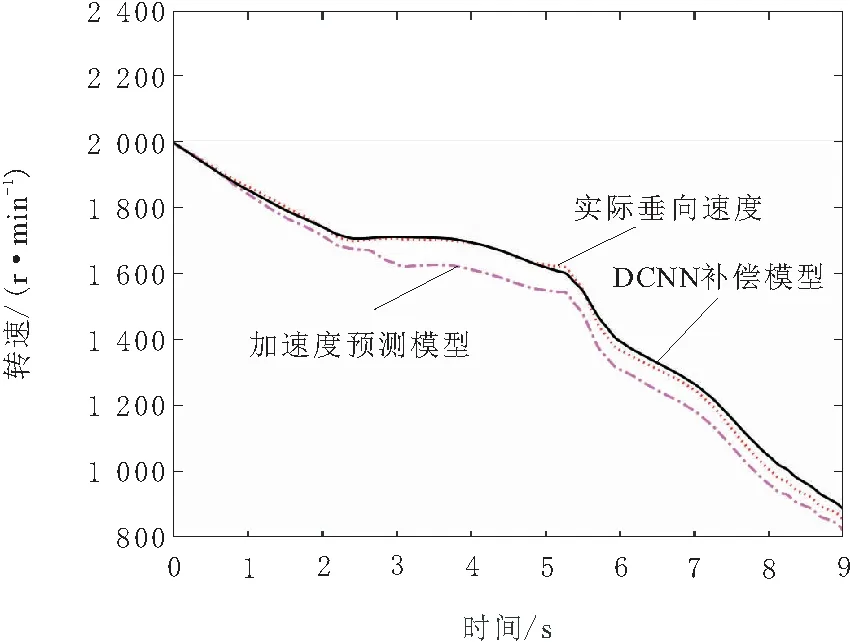
图3 转速对比曲线
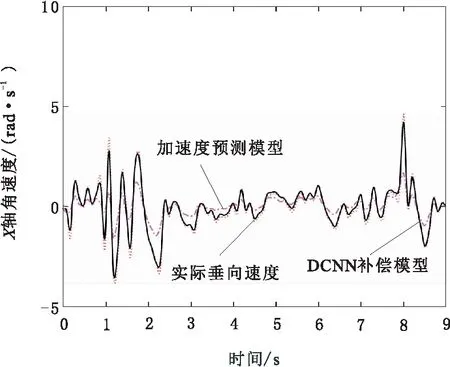
图4 X轴角速度对比曲线

图5 Y轴角速度对比曲线
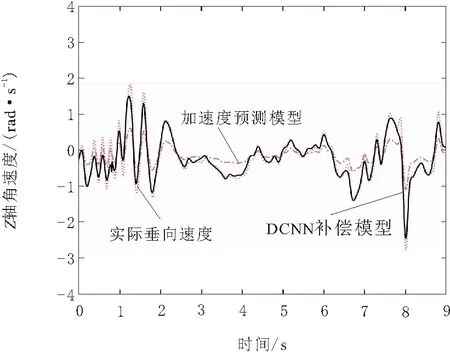
图6 Z轴角速度对比曲线
从图2~图6可以看出,DCNN补偿模型在转速预测、垂向速度预测以及角速度预测方面明显优于加速度预测模型。在其他组测试结果中均满足该结论。
统计在测试样本中加速度预测模型与DCNN偏差补偿模型的均方根误差,得到的均方根误差结果如表3所示。

表3 均方根预测误差对比
从表3可以看出,本文提出的基于DCNN的偏差补偿模型精度明显优于加速度预测模型。
4 结束语
本文主要研究了小型无人直升机自转着陆过程的建模问题。为了补偿加速度预测模型中由于飞行过程中气流以及直升机的抖动的影响带来的建模误差,本文在加速度预测模型的基础上增加了深度卷积神经网络补偿项来补偿建模误差,并利用实际飞行数据对网络进行训练。根据试验结果,改进后的模型可以更好地预测各个状态的变化,精度得到了明显提升。

