基于RULSE方程原理在阜新地区小流域土壤侵蚀量估算中的应用
姜仕琪
(辽宁省大伙房水库管理局有限责任公司,辽宁 抚顺 113007)
小流域综合治理中首先需要对治理流域的土壤侵蚀量进行估算,而土壤侵蚀量较为准确的估算对于小流域综合治理设计参数和指标十分重要[1]。传统土壤侵蚀量主要采用通用土壤侵蚀方程(ULSE方程)进行估算,该方程主要从土壤侵蚀的形成机理进行分析,重点考虑降雨因子、土壤侵蚀因子、估算区域的植被覆盖因子、水保因子以及地形因子,在国内许多区域水土保持规划设计中均得到广泛应用[2- 6]。近些年来,有学者针对传统通用土壤侵蚀方程不能考虑坡面径流对土壤侵蚀的影响,而引入径流因子,对传统通用土壤侵蚀方程进行改进,并在国内一些小流域综合治理的土壤侵蚀量估算中进行应用[7- 10],应用效果均表明相比于传统通用土壤侵蚀方程,其土壤侵蚀估算精度有所改善,尤其在一些具有超渗产流机制的区域,其改善效果更为明显。阜新地区属于辽宁省水土流失较为严重的区域,为提高阜新地区小流域土壤侵蚀的估算精度,本文结合阜新某试验小流域土壤侵蚀观测数据,分别采用修正前后的通用土壤侵蚀方程对其土壤侵蚀量进行估算,对比其土壤侵蚀量的估算精度,研究成果对于阜新地区小流域土壤侵蚀量估算方法的选择具有参考价值。
1 RULSE方程估算原理
修正的通用土壤侵蚀方程主要基于传统通用土壤侵蚀方程,增加坡面径流因子,其估算公式为:
A=11.8×(Q·R·A)0.56·K·C·P·L·CFRG
(1)
式中,A—估算的小流域土壤侵蚀量,t;Q—坡面径流因子,mm;A—估算小流域的面积,hm2;qpeak—降雨侵蚀力因子,MJ/(mm·hm2·h);K—土壤侵蚀因子,t·h/(MJ·mm);C—植被覆盖和管理因子;P—水保措施因子;L—坡度因子;CFRG—粗糙度因子。各因子确定方法如下。
1.1 土壤侵蚀因子K
土壤侵蚀因子主要和土壤类型有关,是土壤侵蚀影响的重要因子,本文主要采用Williams等人研发的土壤侵蚀因子估算方法进行土壤侵蚀因子的确定,该方法对数据要求较少,且估算原理较为简单,方便快速确定土壤侵蚀因子K,其估算公式为:
KULSE=fcsand·fcl-si·forgc·fhisand
(2)
式中,fcsand—土壤质地中粗砂和细砂所占的比例,%;fcl-si—土壤质地中黏土所占的比例,%;forgc—土壤质地中有机物所占比例,%;fhisand—土壤质地中沙土所占的比例,%。各比例估算公式分别为:
(3)
(4)
(5)
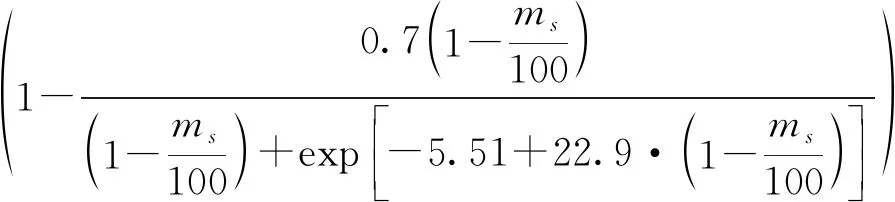
(6)
式中,ms—粒径在0.05~2.00mm的砂粒颗粒所占比例,%;msilt—粒径在0.002~0.05mm的粉粒颗粒所占比例,%;mc—粒径<0.002的黏粒颗粒所占比例,%;orgC—有机质所占比例,%。
1.2 植被覆盖和和管理因子C
植被覆盖和管理因子主要表示为在相同降雨、土壤类型、坡度条件下不同植被覆盖方式下和物植被覆盖裸土方式下的土壤侵蚀量的比值,其变化范围在0~1.0之间,其估算公式为:
C=exp([ln(0.8)-ln(Cmm)]·
exp[-0.00115·rsdsurf]+ln[Cmm])
(7)
式中,rsdsurf—植物在地表残留比例,%;Cmm—植被覆盖和管理因子的最小值,其估算公式为:
Cmm=1.463ln[Caa]+0.1034
(8)
式中,Caa—植被覆盖和管理因子的年均值。
1.3 水土保持措施因子P
水土保持措施因子表示为区域具有水土保持措施和不采取水土保持措施下土壤侵蚀量的比值,其主要和小流域耕作方式、坡度及坡长有关,本文按照Wischmeier和Smith(1978)在不同小流域试验基础上确定的水土保持措施因子关系(见表1)对水土保持措施因子进行确定。
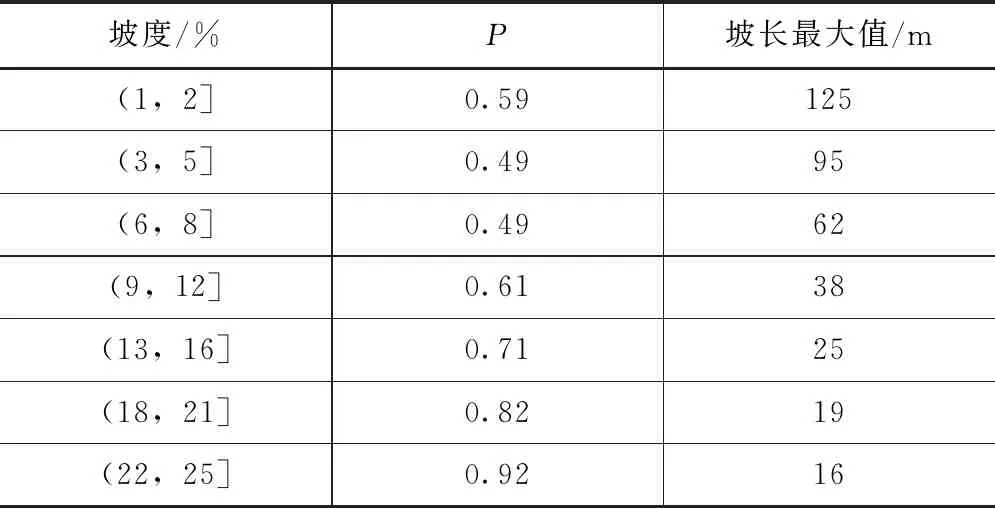
表1 水土保持因子P关系表
1.4 地形因子L
地形因子的估算公式如下:
(9)
式中,Lhill—坡长,m;m—坡长指数;αhill—斜坡角度。坡长指数估算公式为:
m=0.6·(1-exp[-35.835·slp])
(10)
式中,slp—流域平均坡度,‰;αhill和slp之间的估算公式为:
slp=tanαhill
(11)
1.5 粗糙因子CFRG估算公式为:
CFRG=exp(-0.053×rock)
(12)
式中,rock—砾石在土壤质地第一层中的所占比例,%。
2 小流域土壤侵蚀量估算
2.1 主要因子的确定
本文以阜新某径流试验小流域为研究区域,该区域总面积为45km2,区域主要土壤类型分别为石灰性始成土、石灰性冲积土、潜育淋溶土、弱发育淋溶土、石灰性淋溶土、石灰性粗骨土、饱和粗骨土等7种类型土壤,在对各类型土壤质地测定的基础上,采用方程(2)对其土壤侵蚀因子K进行估算,小流域各类型土壤因子见表2。小流域主要土地覆被分别为林地、耕地以及裸体,通过对土地覆被方式下的地表植物量进行调查统计,结合小流域水土保持部门的调查数据,对各类型土地覆被下的植被覆盖和管理因子进行确定,结果见表3。坡面径流因子主要通过小流域径流系数和场次降水进行相乘转化得到其坡面径流深,降雨侵蚀力因子主要采用参考文献[11]中介绍的方法,结合辽宁省无资料地区设计暴雨洪水手册对其进行确定。

表2 研究小流域各类型土壤侵蚀因子确定结果
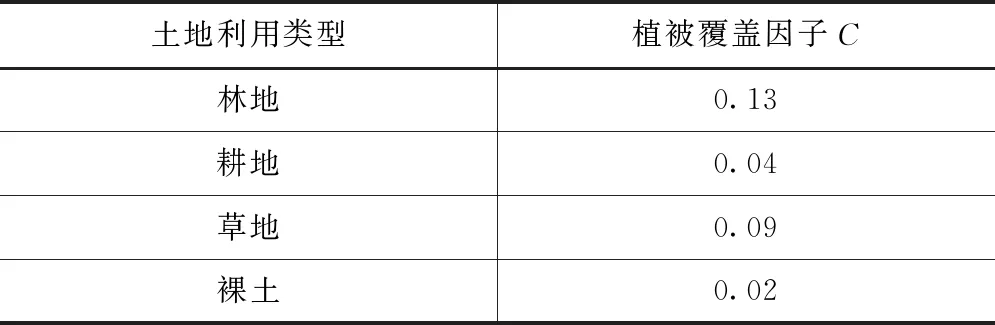
表3 不同土地覆被方式下植被覆盖和管理因子确定结果
2.2 土壤侵蚀量的监测
本次主要以某试验小流域作为研究区域,在径流试验小区底部安装集水池,在每次出现降雨量超过50mm时进行观测,现场安装有虹吸式雨量筒,共观测10组径流试验数据,在集水池的底部设置有大型集水桶,随集水桶内的水量和泥沙量进行测定并进行记录。在水桶内对水样进行搅拌均匀后每次取出1000ml作为试验观测水样,到试验室内对泥沙量进行测定,具体检测方法可详见参考文献[12]。
2.3 土壤侵蚀量的估算
分别采用修正的通用土壤侵蚀方程和传统通用土壤侵蚀方程,结合10组降雨观测数据,坡面径流采用径流系数进行转换得到,其他土壤侵蚀估算因子如2.1节中确定值代入估算,结合10组土壤侵蚀量监测数据,对比分析修正前后通用土壤侵蚀方程的估算精度,结果见表4。

表4 修正前后通用土壤侵蚀方程下土壤侵蚀量估算误差对比结果
从修正前后通用土壤侵蚀方程下土壤侵蚀量估算值和监测值之间的误差对比结果可看出,相比于修正前,修正后的通用土壤侵蚀方程考虑坡面径流因子对土壤侵蚀的影响,总体相对误差均小于修正前的通用土壤侵蚀方程。传统通用土壤侵蚀方程由于只考虑降雨侵蚀的影响,而未能坡面径流因子对土壤侵蚀的影响,尤其是对于超渗产流机制的区域,降雨超过区域土壤下渗能力后基本全部产生坡面径流,因此其对区域土壤侵蚀影响不能有所忽略,修正后的通用土壤侵蚀方程除考虑降雨侵蚀影响外,还增加了坡面径流因子,因此其在阜新超渗产流机制区域其土壤侵蚀估算精度要好于传统通用土壤侵蚀方程,从10组土壤侵蚀监测数据对比结果可看出,相比于传统通用土壤侵蚀方程,在10组观测数据对比下修正后的通用土壤侵蚀方程的土壤侵蚀估相对误差平均可减少9.63%,估算精度得到显著提升。
3 结语
本文结合阜新某径流试验小流域土壤侵蚀监测数据,分别采用修正前后的通用土壤侵蚀方程对比其土壤侵蚀估算误差,相比于传统通用土壤侵蚀方程,修正后的通用土壤侵蚀方程估算误差得到明显改善,10组试验数据相对误差可平均减少9.63%,对于阜新超渗产流机制的区域修正后的通用土壤侵蚀方程土壤侵蚀估算精度更高,适用于阜新地区土壤侵蚀量的估算。

