基于雷达数字孪生的水上多目标跟踪方法研究
徐凯凯,宋利飞,史晓骞,石正坤,孙 昊
(1.武汉理工大学高性能船舶技术教育部重点实验室,武汉 430063;2.武汉理工大学船海与能源动力工程学院,武汉 430063)
1 引言
无人艇(Unmanned Surface Vessel,USV)在航行过程中,可由船舶自动识别系统(Automatic Identification System,AIS)获取周围部分船舶的准确状态(位置、速度和航向),为避碰等运动方式提供信息[1-2],然而所遇到的许多障碍并不都配备AIS,位置信息一般可由无人艇的雷达直接获得[3-4],而速度、方向和航迹等信息需要对雷达采样数据进行多目标跟踪算法处理后获得[5]。
雷达测得无人艇周围障碍物的距离和方位信息,惯性导航/全球定位(Inertial Navigation System/Global Positioning System,INS/GPS)组合导航测得无人艇的坐标和航向信息。无人艇在实际航行一段时间的雷达探测点如图1所示,从中可以看出存在以下问题。

图1 雷达探测Fig.1 Radar detection
(1)雷达和INS/GPS 组合导航采样数据时钟不同步。图中雷达采样点较为稀疏而INS/GPS 组合导航采样点较为密集;
(2)雷达和INS/GPS 组合导航采样数据参考坐标系不同,前者为极坐标系,后者为直角坐标系;
(3)雷达无法分辨出哪些探测点是真正的障碍或杂波,即使分辨出真正的障碍,由于涉及时间维度,也无法直接得到障碍物的航迹和数量;
(4)雷达的采样数据是有误差的,且无法直接探测到机动障碍的状态。
大多数目标跟踪算法利用仿真完成实验,没有将雷达和INS/GPS 组合导航采样数据时钟不同步问题考虑在内,但可以利用插值的方法解决采样时间不同步的问题。常用的插值方法为多项式插值,包括线性插值、牛顿插值和埃尔米特插值等[6]。其中,线性插值只需两个周期的数据,计算步骤简便,在相邻样本数据相差较小时即可满足计算要求,而后两种插值方法涉及到多个周期的数据,属于多项式插值,计算过程较为复杂。
针对雷达和INS/GPS 组合导航采样数据参考坐标系不同问题,需将极坐标系下的探测点转换成无人艇所在的直角坐标系对应的坐标[7]。吉林大学的王鹏宇等[8]研究了传感器载体装载有多个传感器时,由于各个传感器参考的坐标系不同,无法直接探测数据进行处理而需要进行转换的问题。郭云飞等[9]为了减少坐标系转换带来的误差,在极坐标下对目标建立目标跟踪运动模型,通过模拟数据仿真验证了目标跟踪效果。一般雷达的探测范围较小,不需要考虑地球表面因素;INS/GPS 组合导航采样的经纬度在选取正确参考系的情况下,可以最大限度地减小经纬度转平面坐标系的误差,在此基础上进行的极坐标系转化会产生累计误差,但只要保证在一定范围内满足需求即可。针对雷达无法直接得到障碍物的航迹和数量的问题,可以利用关联门,从时间维度上对探测点进行数据关联,剔除多余探测点,获得每个障碍在一段周期内的探测点集合,即每个障碍的航迹。常用的关联门有环形关联门、椭圆关联门和扇形关联门[10]。环形关联门所关联的范围较大,不容易漏掉探测点,后两种关联门则相反,在对目标运动能力掌握较少的情况下,容易漏掉探测点。航迹探测点数据关联常用的方法有最近邻算法、概率数据互联算法、联合概率数据互联算法和多假设法等[11]。其中,最近邻算法最为简便,后3 种关联算法计算方法都较为复杂,计算量大。天津大学的魏存伟等[12]考虑到雷达探测过程中的随机误差、信号处理、设备硬件等因素,对探测点中的孤立野值和离群点进行了剔除处理。湖南大学的黄晶等[13]基于最近邻法对航迹下一时刻的雷达探测点进行筛选,根据关联门的性质去匹配航迹与探测点。国防科技大学的王树亮等[14]考虑到了交叉目标的情况,提出一种概率数据关联算法。Bae S H[15]提到在目标跟踪过程中需要初始化和终止航迹,并剔除重合和错误的航迹。虽然以上文章介绍了航迹的生成方法,但是仅局限于关联门的选择或数据关联方法的介绍,并没有建立完整的航迹管理框架。
针对雷达无法直接探测到机动障碍状态的问题,可以对航迹进行状态估计,以获得该障碍物相对准确的状态信息[16]。运动轨迹状态估计的方法有双向拟合、回归法等数学预测方法,卡尔曼滤波也较多地被用来预测运动物体的状态信息[17]。西安电子科技大学的刘代等[18]针对杂波环境下的目标状态估计问题,提出一种利用多普勒量测状态估计算法,侧重于目标数学运动模型的建立,将观测目标运动模型的径向速度线性化,提高了目标状态精度和算法收敛速度,但该方法仅针对目标匀速情况。海军航空工程学院的王国宏等[19]针对目标测量速度欺骗干扰情况,提出基于速度估计径向投影和运动状态技术延迟的状态估计方法,在仿真实验下有较好的效果。Tlig 等[20]基于卡尔曼滤波成功实现了目标跟踪,但卡尔曼滤波需要准确选取目标运动模型,且部分参数经验性较强,模型和部分参数选取不当,收敛速度大大降低。上述文章都可对目标进行状态估计,但没有提及状态估计后的数据仍需一次时钟对准,以便于后续无人艇避碰时的定时执行。
上述相关文献更多侧重介绍数据关联方法或状态估计等多目标跟踪中的部分步骤,较少对整个雷达多目标跟踪流程中的细节进行介绍,对时钟和空间对准、航迹管理、航迹来源和去向等步骤描述不够详细。本文做出的主要贡献如下。
(1)对雷达和INS/GPS 组合导航的原始采样数据进行多目标跟踪,建立了一套完整的雷达多目标跟踪算法处理流程。
(2)对该算法进行了雷达数字孪生仿真测试,与多项式拟合算法进行对比,验证了本文算法的有效性和稳定性。
2 多目标跟踪方法
2.1 算法架构
多目标跟踪方法的算法架构如图2所示。由于硬件本身采集数据的性能、硬件之间的差异性以及系统各个层级之间的通信延迟等因素,需要对雷达和INS/GPS 组合导航的采样数据进行数据预处理,即无效值剔除、时钟对准和空间对准;在数据预处理后,可以在相同的时间和空间维度对障碍物数据进行航迹管理,基于关联门对探测点进行数据关联;在对航迹分类之后,需要对稳定航迹进行状态估计,以获得机动障碍状态,再进行二次时钟对准,方便定时发送数据。
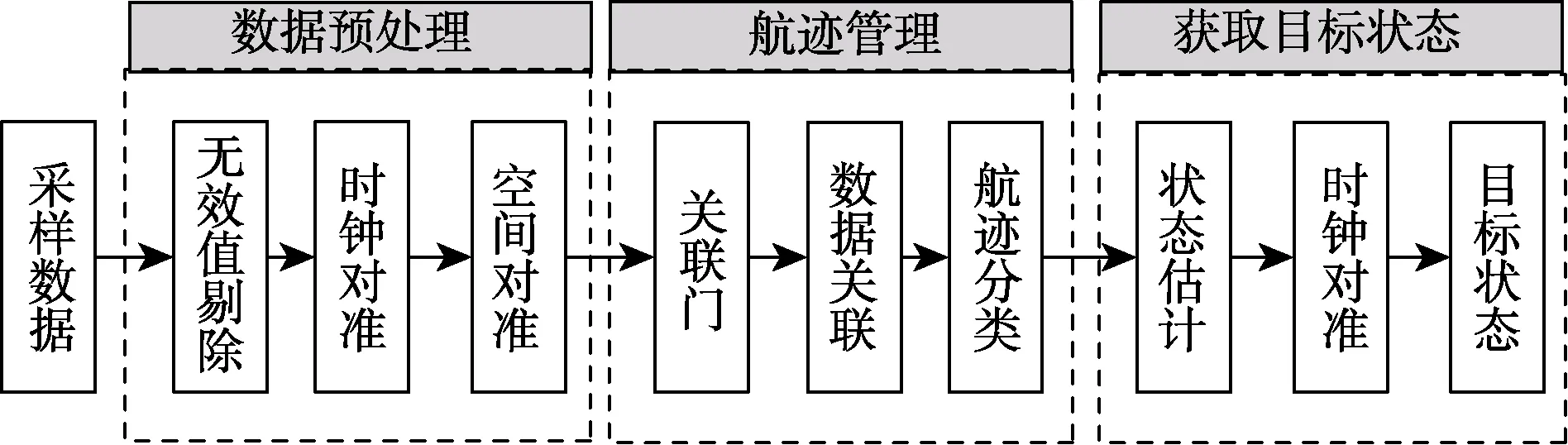
图2 雷达多目标跟踪算法流程图Fig.2 Flow chart of radar multi-target tracking algorithm
2.2 数据预处理
无人艇在航行过程中需要在安全范围内提前感知到周围障碍物以采取下一步行动。所以,只需要保留以无人艇为圆心,半径为安全距离内的雷达数据(如图1 中蓝色圆圈内的探测点),并剔除采样中的空值。

由于两个传感器在无人艇上放置的相对位置一般较近,忽略各自偏差,尽管各自的坐标系不同,但是可以认为其坐标系的原点是在同一个位置。空间转化后的探测点坐标(x z,yz)计算如式(2)所示。
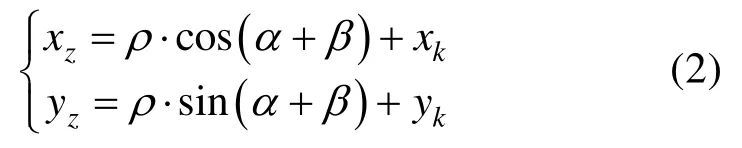
2.3 航迹管理
环形关联门是以障碍航迹末端为中心建立一个由障碍最大和最小运动速度以及采样时间间隔决定的360°环形区域(图3 灰色区域),即障碍可能在下一时刻出现的位置。其内径和外径满足和分别为目标最小速度和最大速度,ΔT为采样间隔。
在同一时刻下,落入关联门的探测点往往不止1 个,可通过最近邻法选择下一个时刻的探测点,主要思想就是选择目标中心点最近的探测点作为下一时刻的目标中心点。所以当多个探测点同时落入关联门内时,选择距离该末航迹点最近的一个探测点作为该机动障碍的下一时刻航迹点,如图3所示,Z(k-1)的下一个航迹点是Z1(k),而不是Z2(k)。

图3 环形关联门Fig.3 Annular association gate
为了方便航迹管理,把航迹分成起始航迹、暂时航迹和稳定航迹3 种,其探测点数量特征、航迹来源和去向如表1所示。

表1 航迹特征、来源和去向Table 1 Track characteristics,source and destination
3 种航迹可能在一段周期的时间内匹配不到新的探测点,这段周期称为航迹剔除时间阈值,分别为T1、T2和T3;当前时刻与每个航迹的末航迹点时间戳差值为ΔTE;令当前时刻的探测点集合z(k),上一时刻所有航迹末点集合为E。航迹管理涉及到空间和时间两个维度、探测点数量、关联门、数据关联和航迹剔除时间阈值等多个变量,其流程图如图4所示。

图4 航迹管理流程图Fig.4 Flow chart of track management
2.4 双向拟合状态估计
基于多项式和粒子群算法(Particle Swarm Optimization,PSO)双向拟合以消除采样误差,对障碍进行状态估计。距离当前时刻太久前的采样数据对当前目标状态估计参考意义不大,探测点数量N= 4是同时获得目标估计位置、速度和航向的最小周期数,如式(3)所示。

雷达的采样误差为r_error,每次采样时间为Tp,采样误差在直角坐标系中体现为在x轴和y轴上的坐标误差。双向拟合误差消除的主要思路是首先用多项式拟合的方法消除y向误差并得到拟合曲线,然后用粒子群算法通过最优化消除x向误差。
2.4.1 多项式拟合消除y向误差
本刊讯(本刊记者)日前,由湖南省期刊协会组织的“湖南省第八届双十佳期刊”“湖南省第二届优秀内部资料”评选工作尘埃落定。本刊等16种期刊及20种内部资料分获殊荣。湖南省期刊协会表示,获得“湖南省第八届双十佳期刊”的16种期刊,皆创刊3年以上,坚持正确的政治方向和出版导向,有较好的舆论引导力、市场竞争力和文化传播力,编校质量优秀、装帧设计精美、印装质量良好,在传统媒体与新兴媒体的融合发展、创新发展上有新思路和新成效,在切实履行“举旗帜、聚民心、育新人、兴文化、展形象” 使命任务中作出了积极贡献。
首先利用多项式对采样点(xi,yi)进行拟合,表示为



图5 坐标系转换Fig.5 Coordinate system conversion
采用式(6)将采样点从坐标系xOy转化为坐标系x′Oy′。

采用式(7)将采样点从坐标系x′Oy′拟合后的曲线转化为坐标系xOy。

2.4.2 粒子群算法修正拟合点消除x向误差
通过多项式拟合,得到拟合之后4 个点,假定首尾采样点x(k-3Tp)和x(k)的位置是正确的,对中间采样点x(k-2Tp)和x(k-Tp)进行修正再次减小误差,满足以下条件:
(1)修正后的x(k-Tp)和x(k-2Tp)与修正前同样满足式(4),即保证目标轨迹是光滑的曲线。
(2)修正后的x(k-Tp)和x(k-2Tp)距修正前的距离小于r_error,即认为估计位置满足雷达的误差精度要求。
(3)修正后的x(k-Tp)和x(k-2Tp)应满足式(3)中加速度改变量 Δa(k)尽量小。
基于此,采用粒子群算法对x(k-Tp)和x(k-2Tp)的位置进行优化求解。如图6所示,将x(k-Tp)和x(k-2Tp)的横坐标值作为二维粒子x(k-Tp)和x(k-2Tp),并带入对应多项式曲线拟合公式得到y(k-Tp)和y(k-2Tp),此时两点分别为(xk-Tp,yk-Tp)和(xk-2Tp,yk-2Tp),与真实值的距离集合为di={d k-1,dk-2},则该距离对目标函数的影响可表示为罚函数H
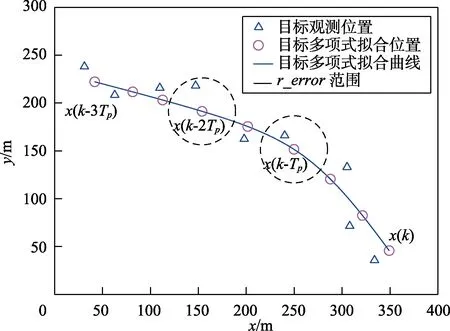
图6 粒子群算法消除x 向误差Fig.6 PSO eliminate x-direction error

式中,i=t- 1,t- 2。
适应度函数表示为使修正后的4 个采样点的Δa最小,表示为
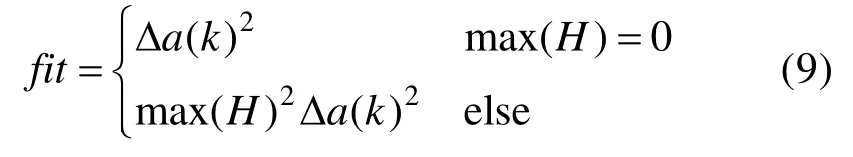
双向拟合估计的计算流程如下:
Step2:按照式(6)对坐标系xOy的进行坐标旋转,得到坐标系x′Oy′下的坐标,对进行多项式曲线拟合,得到拟合后的曲线函数,将′中的横坐标代入,得到坐标,多项式曲线拟合前后的横坐标是相同的。
Step3:在坐标系x′Oy′下,将两个中间时刻的采样点横坐标作为粒子,式(9)为适应度函数,采用 PSO 求解最优,带入得到,得到坐标系x′Oy′下的估计位置,并按照式(7)转为坐标系xOy下的坐标,得到估计位置。此外,估计位置需要按照式(1)进行第二次时钟对准。
3 仿真结果及分析
3.1 本文目标跟踪算法仿真
以安装雷达和INS/GPS 组合导航的无人艇所采集到数据集进行数字孪生仿真测试。以无人艇初始位置为原点,将所有时刻的障碍物相对位置转化到对应的直角坐标系内。通过关联门对探测点进行航迹分类。t=40.66s 时,如图7(a)所示,有4 个孤立探测点,为起始航迹;3 条航迹的探测点个数还不到5 个,为暂时航迹;2 条航迹的探测点个数已超过5 个,为稳定航迹。t=98.71s时,如图7(b)所示,起始航迹、暂时航迹和部分稳定航迹已经被剔除,环境中的杂波已经完全过滤,形成了5 条稳定航迹。
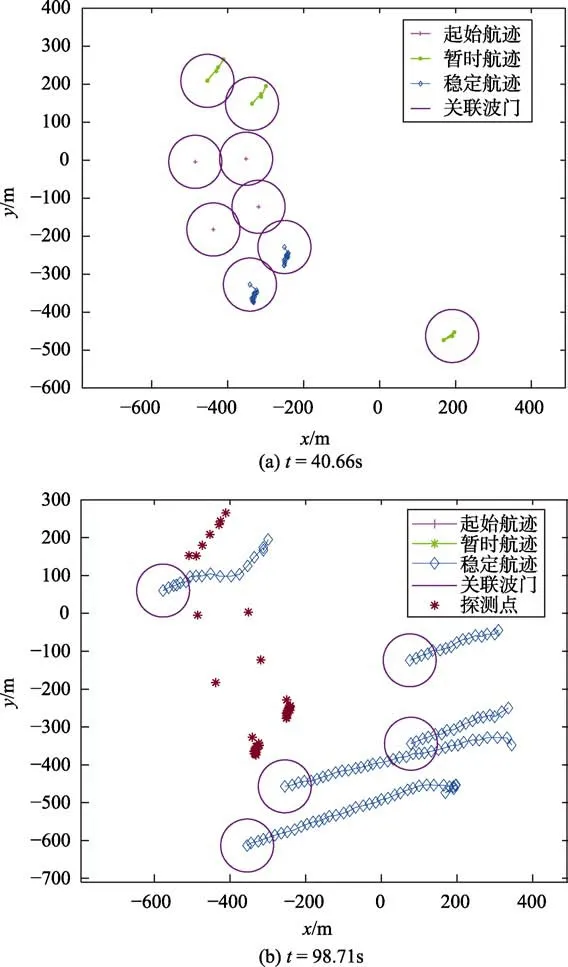
图7 航迹管理Fig.7 Track management
稳定航迹形成时,便可运用双向拟合算法对稳定航迹进行状态估计,以求得机动障碍相对准确的位置、速度和航向信息。从图8(a)可以看出,原始航迹的采样点比较曲折,航迹连线并不平滑,经过双向拟合算法后,其估计航迹连线平滑了,更符合机动障碍的运动规律。
图8(b)和(c)分别是利用双向拟合算法对原始航迹处理所得到的估计速度和航向。可以看出,速度估计趋势较为平缓,而前若干个探测点的航向变化较大,原因在于,机动障碍初始速度较小,位置变化较小,待障碍速度提升之后,双向拟合算法可以进行相对准确的估计,机动障碍的速度和航向在若干采样周期之后,已经趋于稳定。
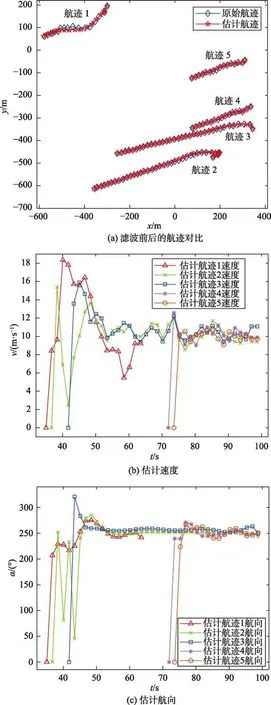
图8 状态估计Fig.8 State estimation
3.2 对比仿真分析
以航迹1 为例,将真实航迹、稳定航迹、本文目标跟踪航迹和多项式拟合航迹作对比,如图9所示。可以看出,两种算法的轨迹都较为平滑,本文目标跟踪航迹与真实航迹的重合度较高;多项式拟合算法与稳定航迹的重合度较高,且易产生过拟合和欠拟合的情况。其原因在用本文目标跟踪方法在状态估计时,第一步拟合的采样点较少,且第二步经过一次粒子群算法修正。

图9 航迹1 对比Fig.9 Track1 comparison
将本文目标跟踪算法与多项式拟合算法进行性能对比,性能指标采用障碍空间位置均方根误差(Root Mean Square Error,RMSE)和速度RMSE,计算公式如式(10)所示。

图10 和图11 分别是两种估计算法的位置RMSE和速度RMSE变化曲线,可以看出本文目标跟踪算法的RSME在前期有些不稳定且高于多项式拟合算法,经过5 个周期之后便逐渐下降并趋于平稳;多项式拟合算法整体处于平稳,但局部波动较大。通过对比,验证了本文所提算法的有效性和稳定性。

图10 位置RMSE 曲线Fig.10 RMSE curve of position
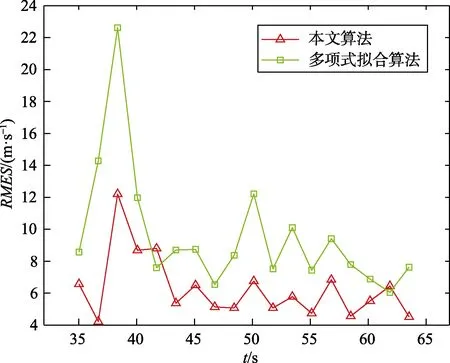
图11 速度RMSE 曲线Fig.11 RMSE curve of velocity
两种算法的时间复杂度差别主要在于状态估计所采用的方法不同,只考虑状态估计步骤,忽略O(1)、矩阵转置等较小的复杂度,本文目标跟踪算法时间复杂度为O(8m+mn+glm2),其中,m为观测数据维数;n为状态维数;g为粒子群算法中的种群规模;l为迭代次数。
多项式拟合算法的时间复杂度为O(8m+mn)。理论上本文目标跟踪算法花费的时间更多,但仍需以实际时间为准。
如表2所示,与多项式拟合算法相比,本文目标跟踪算法的位置RMSE 均值和速度RMSE 均值更小,而本文目标跟踪算法平均每步运算时间与多项式拟合算法平均每步运算时间之间的差别很小,说明本文目标跟踪算法在跟踪精度方面具有一定的优势。
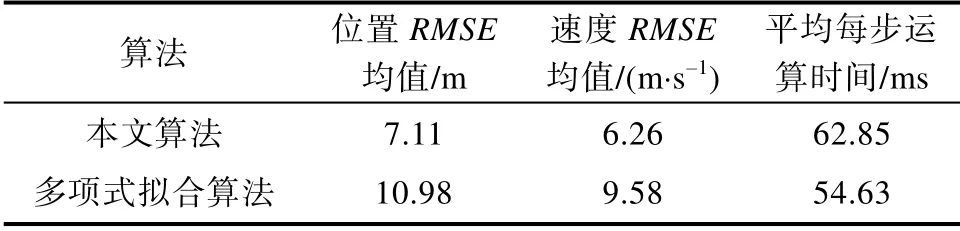
表2 两种算法数据对比表Table 2 Data comparison table of two algorithms
4 结论
本文研究了基于雷达数字孪生的水上多目标跟踪方法。以雷达和INS/GPS 组合导航采样的数据为样本,进行了预处理,使两种传感器的数据可在相同的时间和空间维度进行计算,并通过环形关联门和最近邻数据关联实现了对航迹的分类,建立了航迹管理流程,最后运用双向拟合算法对机动障碍的位置、速度和航向进行数字孪生仿真测试,结果优于多项式拟合算法。
未来可从数据关联、航迹管理和状态估计等多方面对多目标跟踪算法进行优化,以应对更加复杂的情况,比如交叉航迹分类,更快地识别障碍的出现和消失时间点,更加精确地估计机动障碍位置、速度和航向等。

