基于二层分解技术和改进神经网络的河流溶解氧预测研究

陶志勇，胡启振，任晓奎

(辽宁工程技术大学 电子与信息工程学院，辽宁 葫芦岛 125105)

河流中溶解氧（Dissolved Oxygen, DO）能反映水质污染程度和水体自身净化能力[1]，是衡量水质优劣的重要指标之一. 当河流受到有机物污染，水体的复氧速度赶不上分解有机物的耗氧速度时，会导致溶解氧含量快速下降，造成水中需氧生物和各种鱼类的死亡[2]. 研究发现，水体复氧不利是河流水质恶化的主要原因[3]. 因此，准确预测未来河流中溶解氧的含量，掌握它的变化趋势，可以及时做好河流污染防治工作，对生态环境的保护具有重要意义.

目前，溶解氧预测方法主要有统计预测、机器学习预测以及组合模型预测等. 统计预测的常用模型有差分自回归移动平均模型（Autoregressive Integrated Moving Average Model，ARIMA）[4]等，如黄玥等[5]应用ARIMA 模型对三峡库区出口和入口端的DO 等水质数据进行预测. 随着人工智能技术的发展，机器学习中的人工神经网络和支持向量机(Support Vector Machines，SVM)被广泛应用到水质预测中，李鑫鑫等[6]用遗传算法（Genetic Algorithm，GA）优化神经网络的权值和阈值，建立GA-BP 神经网络模型对水质参数进行预测. 由于河流中溶解氧的质量浓度参数具有非线性和不稳定性的特征，较为复杂，难以进行数学建模[7-8]，所以单一模型预测精度较低. 为解决上述问题，刘晨等[9]提出EEMD-FA-SVM 的组合预测模型，首先用集合经验模态分解（Ensemble Empirical Mode Decomposition，EEMD）削弱DO 序列的复杂性，得到相对稳定的子序列，然后将子序列分别用萤火虫算法优化的SVM 做预测，将各分量预测结果叠加，得到最终的预测结果. 卢毅敏等[10]提出CEEMDANSE-CS-Elman 组合预测模型，首先用自适应噪声的完整集成经验模态分解（Complete Ensemble Empirical Mode Decomposition with Adaptive Noise，CEEMDAN）对DO 序列降噪，然后计算各分量的样本熵值，将熵值相近的序列进行合并，最后将各个序列分别进行预测并将结果叠加，得到最终结果. 组合模型虽提升了DO 预测精度，但是EEMD和CEEMDAN 分解后的高频率本征模函数（Intrinsic Mode Functions，IMF）易受到随机因素的影响[11-12]，序列复杂性相对较高，导致模型预测精度降低.

在上述研究的基础上，本文提出TDT-SSA-BP组合预测模型，首先应用二层分解技术，将CEEMDAN 分解后的高频率IMF 用变分模态分解（Variational Modal Decomposition，VMD）再次处理，从而充分削弱DO 序列的非线性和不平稳性；然后提出麻雀搜索算法（Sparrow Search Algorithm，SSA）优化神经网络的溶解氧预测模型，其中SSA 是2020 年提出的新型群智能优化算法，具有更好的全局搜索和局部寻优的能力以及更快的收敛速度[13]；接下来将二层分解得到的所有分量输入到SSABP 模型中，得到各分量的预测结果，把各分量预测结果重构，即得到最终的预测结果. 通过实验分析，本文所提模型相比于单一模型或其它组合模型拥有更高的预测精度.

1 模型介绍

本文所提TDT-SSA-BP 组合预测模型架构如图1 所示. 具体步骤如下：

图1 TDT-SSA-BP 模型流程图Fig. 1 Flow chart of TDT-SSA-BP model

步骤 1 采集DO 质量浓度时间序列数据，对序列进行预处理，形成数据集.

步骤 2 采用CEEMDAN 算法对数据集进行第一层分解，得到模态分量IMF1，IMF2，···，IMFn-1和余量Residual.

步骤 3 用PE（Permutation Entropy，PE）计算步骤2 中第一层分解后各分量的排列熵值.

步骤 4 将排列熵值较高的模态分量采用VMD 算法进行第二层分解，得到新的模态分量Mode1，Mode2，···，Modem.

步骤 5 使用SSA 算法优化BP 神经网络的权值和阈值，建立SSA-BP 预测模型.

步骤6 把步骤2 和步骤4 中分解得到的所有模态分量输入到SSA-BP 预测模型中，得到子序列的预测结果.

步骤7 重构子序列的预测结果，得到最终的DO 质量浓度预测结果.

1.1 数据预处理 由于设备故障或者人为等原因，采集到的原始DO 质量浓度（mg/L）时间序列存在离群值和缺失值的情况. 若对离群值和缺失值不做处理，会造成时间序列数据起伏过大或者间断，导致预测精度降低.

鉴于此，依据GB3838—2002《地表水环境质量标准》和箱线图剔除离群值，因为缺失数据较少且短时间内DO 质量浓度不会有大幅度的波动，所以本文选择中位数填充法对离群值和缺失值进行填充.

此外，为提升预测模型的收敛速度和精度，在输入神经网络前需对数据集进行归一化处理，公式如下：

1.2 二层分解技术

步骤 3 重复执行步骤1 和步骤2，当余量信号的极值点不超过2 个，此时余量无法继续分解，最终DO 时序信号可表示为：

1.2.2 变分模态分解 相比于经验模态分解，VMD[15]具有更完备的数学理论支撑，通过对排列熵值较高的IMF 分解，可有效降低时间序列的非线性和不稳定性. 设DO 时间序列信号f(t)分解为有限带宽的模态分量uk(t)且 中心频率为 ωk，其算法步骤如下：

步骤 1 用Hilbert 对模态分量uk(t)进行处理，得到解析信号和单边频谱.

步骤 2 将解析信号中混合中心频率 e-jωkt，从而可将每个模态的频谱转换到基带上.

步骤 3 通过高斯平滑计算uk(t)的带宽.

因此，产生变分约束问题可表示为：

1.3 SSA-BP 预测模型及原理

1.3.1 麻雀搜索算法 SSA 算法通过模拟麻雀觅食的生物特性，将麻雀分为发现者、加入者和侦察者. 其中发现者负责寻找食物源，占种群的10%～20%；加入者则通过跟随发现者来寻找食物；侦察者受到威胁时，位于种群边缘的麻雀会向安全区移动，位于群体中央的麻雀会随机移动，从而避免被捕食者攻击.

发现者位置更新如下所示：

1.3.2 BP 神经网络 BP 神经网络是多层前馈型神经网络，通常由输入层、隐含层和输出层3 层网络结构组成，如图2 所示，各层神经元之间是全互连连接，同一层中的神经元之间互不相连，且传递函数一般采用sigmoid 函数.

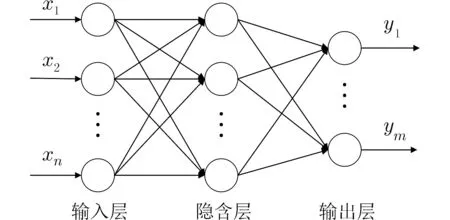
图2 单隐含层BP 神经网络拓扑结构Fig. 2 Topological structure of single hidden layer BP neural network

BP 网络主要由信号的正向传输和误差的反向传递两个阶段组成. 第一个阶段中，输入信号由输入层进入神经网络，然后经过隐含层神经元的处理 ，最后到达输出层. 第二个阶段中，若输出结果和实际结果之间的误差不在设定的范围内，则会进行误差的反向传递，由输出层经隐含层传入到输入层，并不断地调整神经元之间的权值和阈值使误差降低，此过程反复循环，直到满足精度要求或者达到最大迭代次数时，训练结束. 由于BP 神经网络具有较好的自学习和非线性映射能力，目前被广泛应用在各个领域.

1.3.3 麻雀搜索算法优化神经网络 BP 神经网络通过梯度下降法改变权值和阈值，但在训练过程中易陷入局部最优解. SSA 算法具有更好的全局搜索和局部寻优的能力，用来调整神经网络的权值和阈值，可有效提高预测精度.

SSA-BP 预测模型建立步骤如下：

步骤 1 选取样本数据，对数据作归一化处理，按一定比例划分为训练集和测试集；确定神经网络的隐含层层数以及各层神经元个数.

步骤 2 设置麻雀种群规模为20，最大迭代次数为100，发现者比例为0.2，警戒值为0.8.

步骤 3 生成初始种群位置，用预测值和真实值的误差矩阵的范数作为适应度函数的输出，计算所有个体的适应度值，并根据适应度值的大小排序.

步骤 4 将适应度值较大的前4 个麻雀作为发现者，根据位置更新公式（8）进行全局搜索；剩余的麻雀作为加入者，会跟随发现者觅食，根据位置更新公式（9）进行局部搜索；当侦察者意识到危险时，也会根据位置更新公式（10）进行局部搜索.

步骤 5 保存拥有最佳适应度值的麻雀位置，若达到最大迭代次数时，则迭代结束，否则重复步骤3 ～ 4，不断更新最佳适应度值.

步骤 6 将步骤5 中得到的最优解作为神经网络的权值和阈值，建立SSA-BP 模型.

2 实验及分析

2.1 数据来源 本文数据来源于2016 年10 月21日至2017 年11 月21 日江苏省无锡市长江水质实时监测站，监测频率为每日一次，共计397 个数据，经预处理后，数据集如图3 所示. 从图3 中可以看出，DO 时间序列具有明显的随机性和不平稳性.选 取2016 年10 月21 日 至2017 年10 月15 日 共计360 个数据作为训练集，剩余2017 年10 月16日至11 月21 日共37 个数据作为测试集.

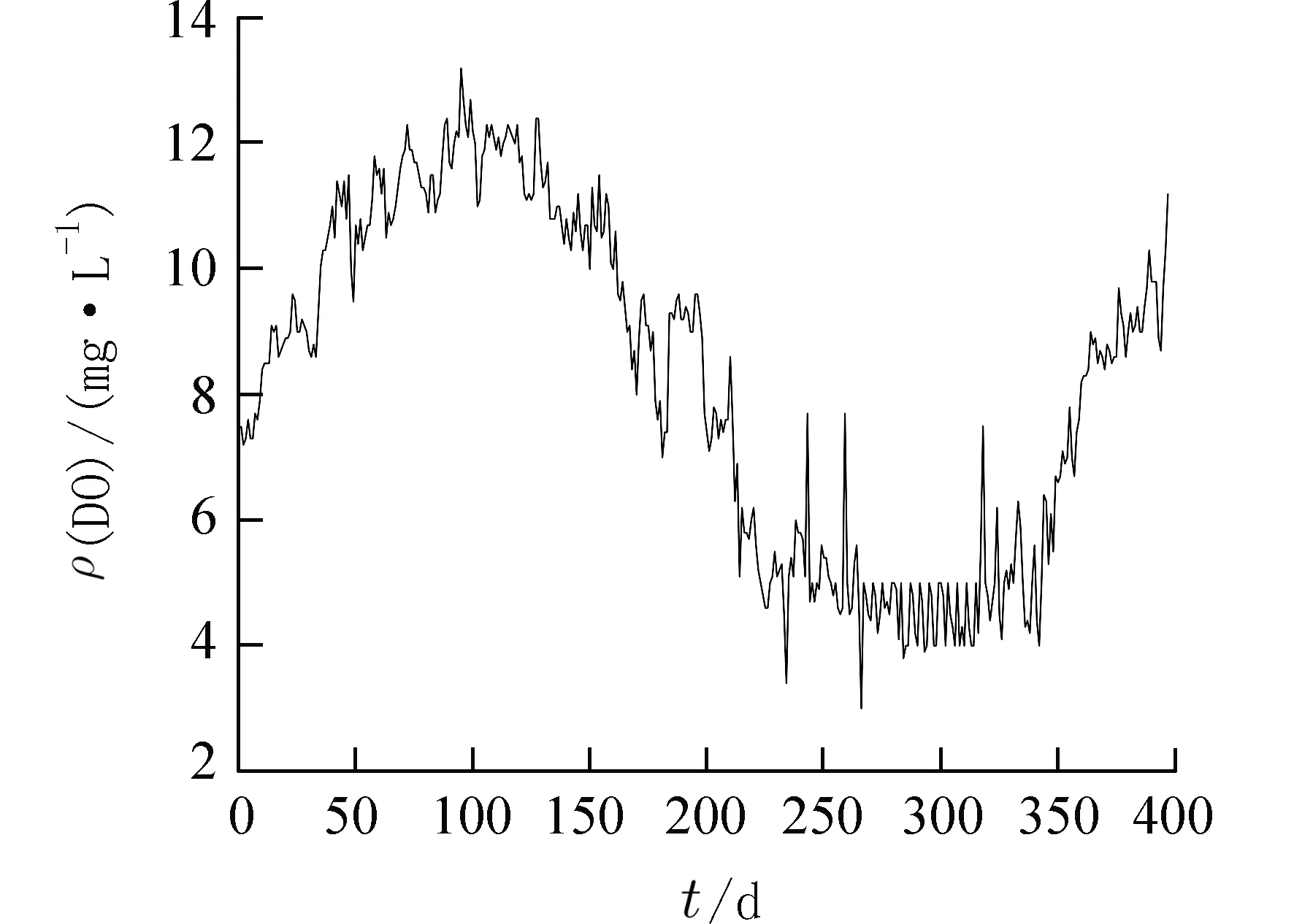
图3 原始DO 质量浓度时序数据Fig. 3 Original DO concentration time series data

2.2 评价指标 本文采用4 种评价指标直观地展示各个模型的预测效果，分别是平均绝对误差（Mean Absolute Error，MAE）、均方根误差（Root Mean Square Error，RMSE）、平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）和决定系数R2，计算公式如下：

2.3 实验仿真 首先使用CEEMDAN 分解DO 时间序列，得到IMF1，IMF2，···，IMF7和Residual，结果如图4 所示. 由图4 可知，IMF1具有较为复杂的波动特征，反映DO 序列受到随机影响；IMF2～IMF7序列相对平稳且具有一定的周期性；Residual时频特征平缓下降，反映了DO 时间序列的长期趋势.

图4 CEEMDAN 分解DO 时间序列结果Fig. 4 DO time series results of CEEMDAN decomposition

接下来计算各分量的排列熵值，如图5 所示.由图5 可知，各个分量的排列熵值整体呈下降趋势，说明序列的复杂程度和随机性在逐渐减小. 其中IMF1的熵值远高于其他分量的熵值，可知IMF1时间序列的波动特征较为复杂，受到随机因素的影响较大.

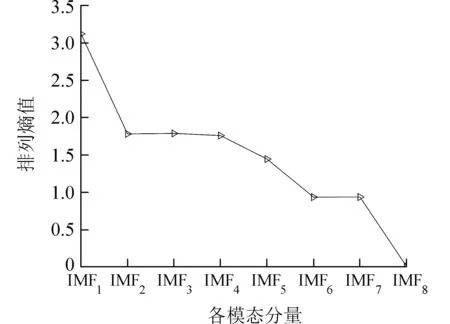
图5 各分量排列熵值Fig. 5 Permutation entropy of each subcomponent

根据各序列的排列熵值以及考虑到预测效率的原因，本文仅对熵值较高的分量IMF1使用VMD进行二次分解. 由于VMD 的模态分解个数K需要人为选择，本文采用文献[16]中的方法，其文献是依据VMD 分解之后各模态分量的中心频率来确定是否出现了过分解现象，若当前模态分量的中心频率差值远小于其它K值下的差值时，则表示VMD 出现过分解现象，此时的K-1 就是最佳分解个数. 另外VMD 分解的其它初始参数中，惩罚因子设为1 000, 噪声容忍度设为0. 不同分解个数K下的中心频率如表1 所示.

表1 不同K 值下VMD 分解的中心频率Tab. 1 VMD decomposition center frequency at different K values

从表1 中可以看出K=7 时，模态分量中心频率的最小差值仅为81×10-6，远小于K=2～6 时中心频率的差值，所以认为K=7 时，VMD 出现了过分解现象. 另外，分解个数过多也会增大计算规模，所以最终选择IMF1的VMD 模态分解个数为6，分解结果如图6 所示.

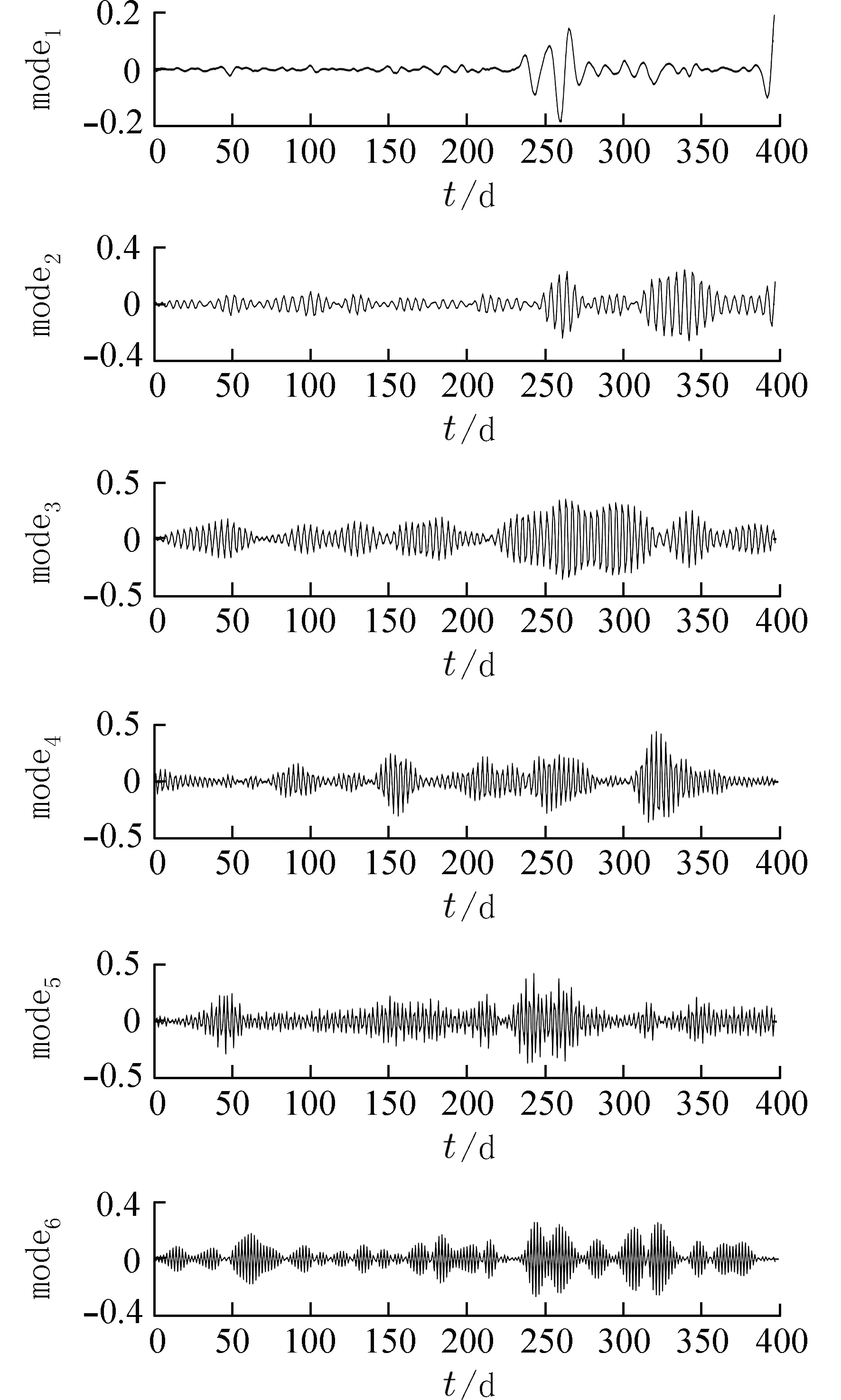
图6 VMD 分解IMF1 结果Fig. 6 VMD decomposition result of IMF1

至此，原始DO 时间序列经过二层分解后，得到 分 量imf1，imf2，···，imf13，其 排 列 熵 值 如 图7所示. 由图7 可知，经过VMD 的分解显著降低了IMF1序列的复杂度.

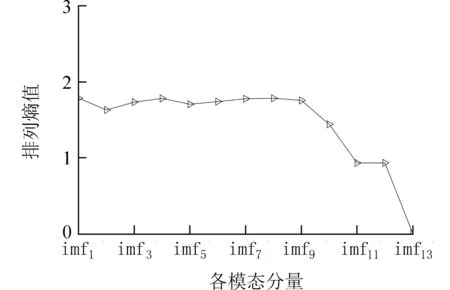
图7 二次分解后各分量排列熵值Fig. 7 Permutation entropy of each component after quadratic decomposition

将经过二层分解得到的分量输入到麻雀搜索算法优化的神经网络模型中，在预测过程中，使用连续3 d 的DO 数据预测第4 d 的DO 数据，得到各分量的预测值，然后叠加各个分量的预测值，即可得到最后的DO 时间序列预测质量浓度.

2.4 模型对比分析与评价 为验证本文所提TDTSSA-BP 模型的有效性，共设置两组对比实验进行分析与评价. 实验所用麻雀搜索算法和粒子群算法的种群数均设为20，最大迭代次数均设为100，神经网络隐藏层神经元个数设为5，其它网络参数均做相同设置.

第1 组对比试验：用本文所提模型与BP、SSABP、 CEEMDAN-SSA-BP、 VMD-SSA-BP、 TDTPSO-BP 模型做对比，结果如图8 所示. 从图8 中可以看出，BP 模型和SSA-BP 模型与实际值相比存在预测结果滞后的现象，采用CEEMDAN、VMD或者二层分解的模型能及时反映数据的变化，有效克服了预测滞后现象，本文所提模型的预测结果更贴近真实值，其各模型误差对比如表2 所示.

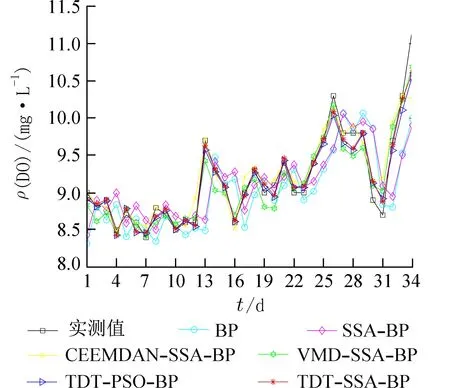
图8 第1 组不同模型预测结果Fig. 8 Prediction results of the first group of different models

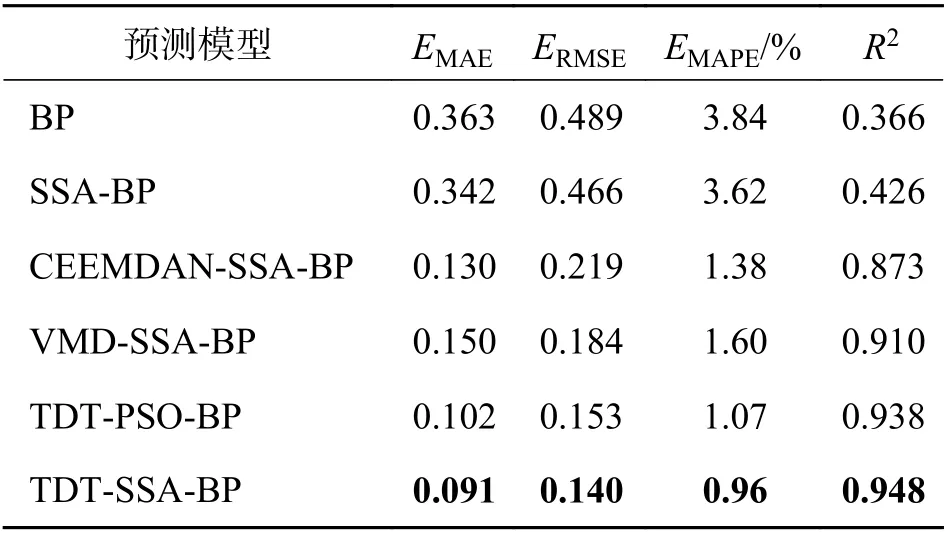
表2 不同模型精度对比Tab. 2 Accuracy comparison of different models

由表2 可知，CEEMDAN-SSA-BP 模型相比于SSA-BP 模型MAE、RMSE 和MAPE 分别减少了62%、53%和62%，R2增加了105%，VMD-SSA-BP模型相比于SSA-BP 模型MAE、 RMSE 和MAPE分别减少了56%、61%和56%，R2增加了114%. 表明使用CEEMDAN 或VMD 对DO 时间序列单次分解可以有效提高预测精度.

本文所提预测模型与CEEMDAN-SSA-BP 模型对比，MAE、RMSE 和MAPE 分别减少了30%、36%和30%，R2增加了9%，与VMD-SSA-BP 模型相比，MAE、RMSE 和MAPE 分别减少了39%、24%和40%，R2增加了4%，表明二次分解技术比单次分解更显著地提升了模型的预测精度.

与TDT-PSO-BP 模型对比，本文模型MAE、RMSE 和MAPE 分别减少了11%、8%和10%，R2增加了1%. 图9 为两种模型的Mode1序列预测的收敛曲线对比. 表明在做DO 时间序列的预测时，SSA 比PSO 收敛速度更快且具有更强的寻优能力.第2 组对比实验：用本文所提模型与ARIMA[5]、GA-BP[6]和EEMD-PSO-SVM[9]溶解氧预测模型做对比. 结果如图10 所示，由图10 可知，TDT-SSABP 模型预测曲线更贴近真实值，误差对比如表3所示.

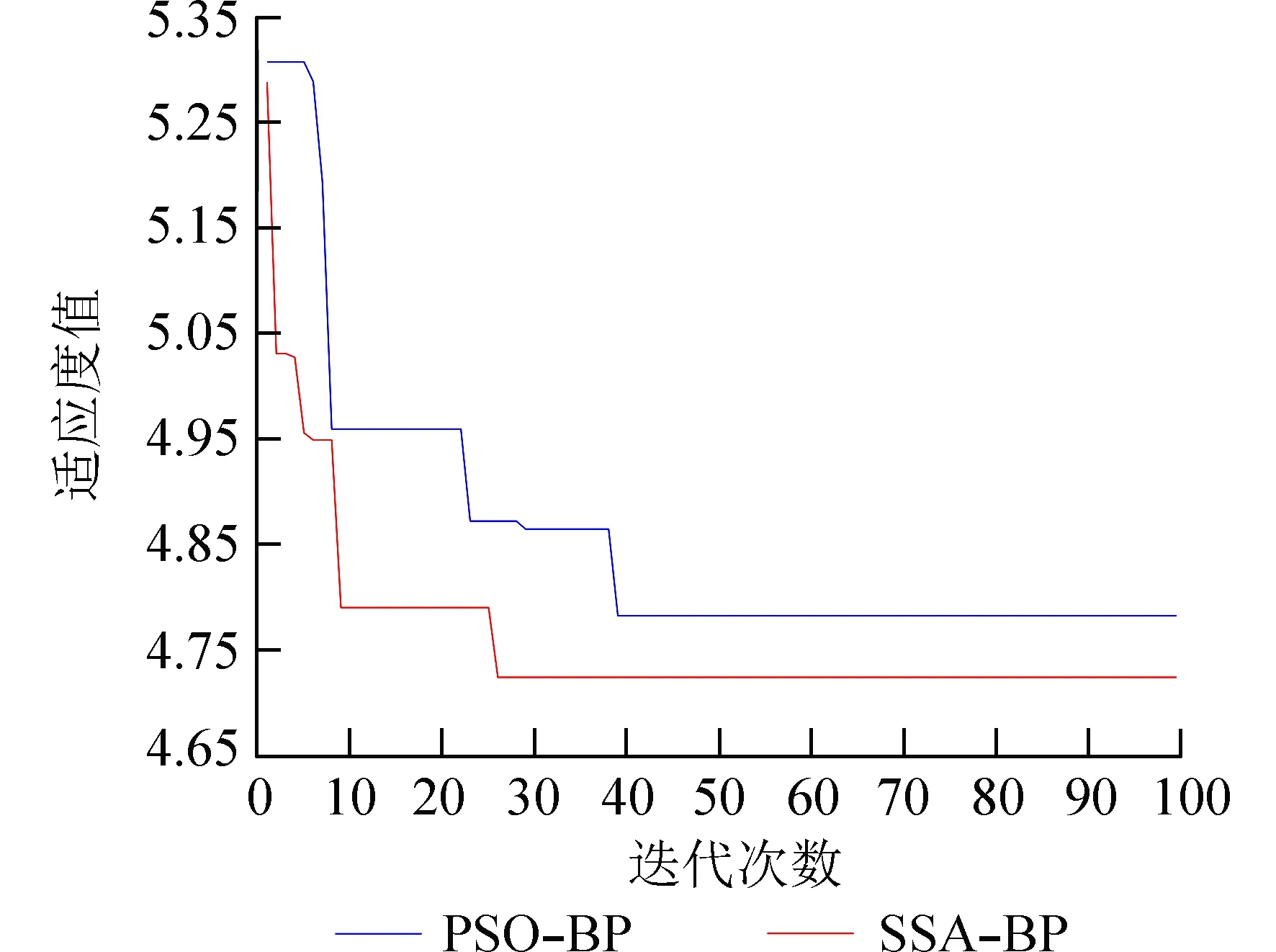
图9 不同算法收敛曲线Fig. 9 Convergence curves of different algorithms

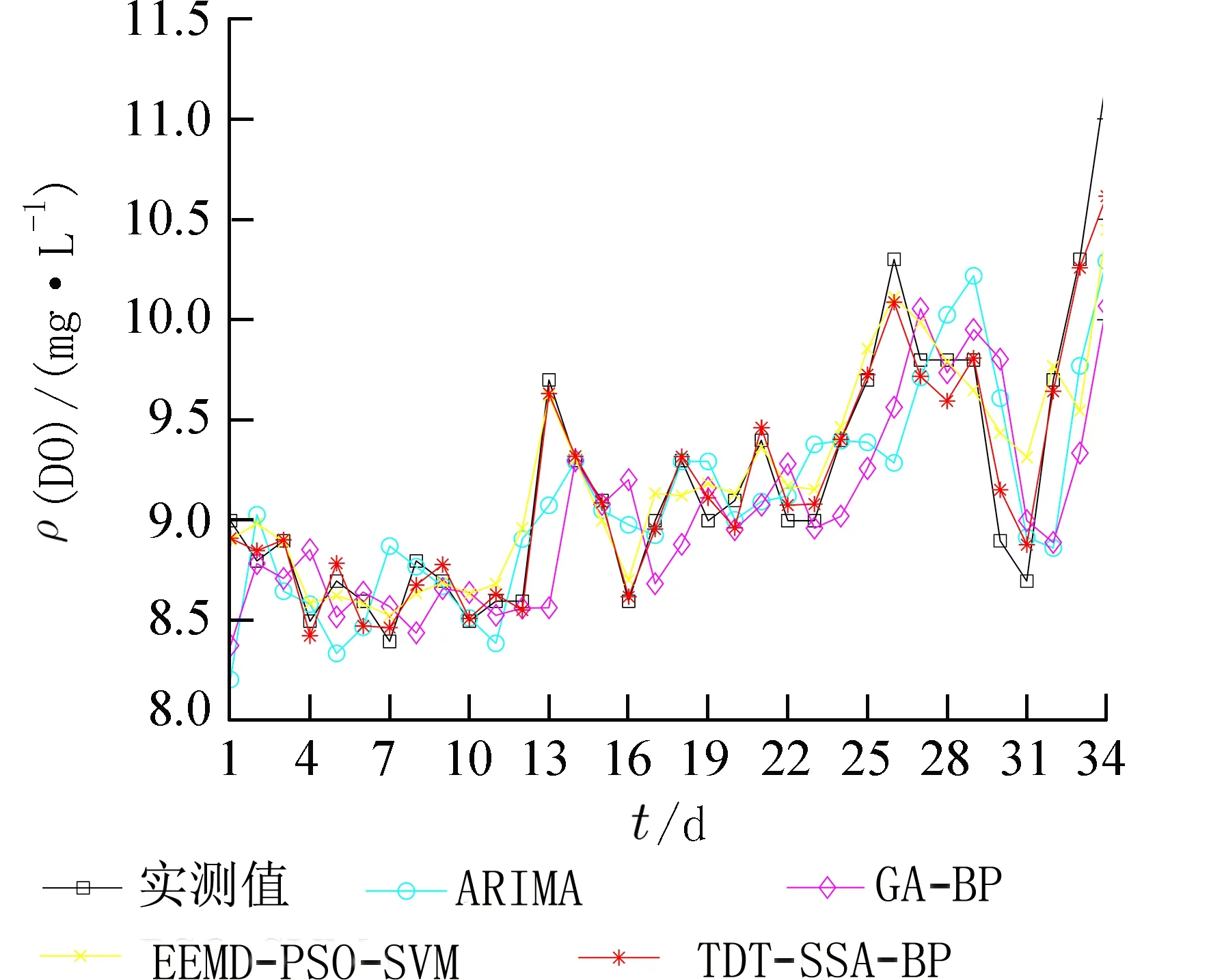
图10 第2 组不同模型预测结果Fig. 10 Prediction results of the second group of different models

由表3 可知，本文所提模型与ARIMA 模型相比MAE、RMSE 和MAPE 分别减少了71%、66%和71%，R2增加了74%，与GA-BP 模型相比MAE、RMSE 和MAPE 分别减少了74%、71%和74%，R2增加了134%，与EEMD-PSO-SVM 模型相比，MAE、RMSE 和MAPE 分别减少了63%、57%和63%，R2增加了32%，表明了本文模型与其它已报道模型相比，预测精度有显著提高.

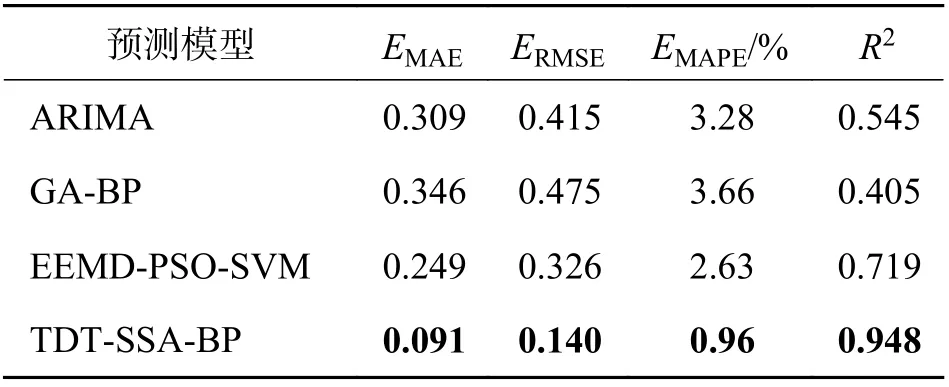
表3 本文模型与现有模型精度对比Tab. 3 The accuracy of this model is compared with the existing models

3 结论

为克服河流溶解氧质量浓度序列的非线性和不平稳性造成的预测精度难以提高的问题，本文提出了TDT-SSA-BP 预测模型. 首先应用二层分解技术充分削弱序列的非线性和不稳定性，与单次分解技术相比，预测精度得到了显著提升；其次本文提出使用寻优能力更强的SSA 算法优化神经网络的权值和阈值并与PSO 算法做对比，所提SSA-BP 溶解氧预测模型取得了更高的预测精度且收敛速度更快；最后通过与现有的其它溶解氧预测模型做对比，TDT-SSA-BP 模型预测精度最高，进一步验证了本文所提模型的有效性. 在后续的研究中，考虑融合二层分解技术和深度学习预测模型，进一步提高预测精度.