随机运输时间下集装箱海铁联运箱流径路优化方法*

袁雪丽 杨菊花▲ 任金荟

（1. 兰州交通大学交通运输学院 兰州 730070；2. 中国铁路兰州局集团有限公司兰州货运中心安全生产部 兰州 730030）

0 引 言

由海上丝绸之路经济带的兴起和迅猛发展可以看出，国际货物的流通对于各个国家经济发展和政治稳定有重要推动作用。作为1种新型的物流运输组织模式，集装箱海铁联运具有低成本、高效率、便管理、快周转的优点，为促进货物流通并响应国家“公转铁”以及多式联运的发展战略，海铁联运的推进刻不容缓。在煤炭、石油等传统能源短缺，太阳能、风能、氢能等新生能源蓬勃兴起，以及2022年铁路电气化率达到73.8%的背景下，以电力牵引区段为例研究海铁联运箱流径路优化问题对于实现交通运输业的“碳达峰、碳中和”目标具有现实意义。

为避免各种突发状况的发生，国内外学者针对运输过程中的不确定因素进行了深入研究。赵祎[1]采用随机模拟技术、神经网络和遗传算法相结合的混合式启发算法求解随机环境下的海铁联运箱流径路优化模型。但其模型和算法基于一站直达式列车，运输途中无中转换装作业，未考虑货源不充足的情况。张丰婷等[2]在考虑顾客需求时间窗的情况下，将装卸箱服务时间采用不确定规划区间处理求得多目标海铁联运路径规划模型。但目标归一化处理不能体现出各个解的优越性。王琴等[3]采用三角模糊数表示不确定客户需求量解决了不确定环境下危险品运输车辆多目标优化问题。Sun 等[4]考虑伤亡人数、救援物资数量和运输时间等的不确定性，以总成本和伤亡最小为目标解决灾后应急物流问题。Zhang等[5]在兼顾不确定充电时间、行驶时间以及服务时间的情况下对共享式自动驾驶电动汽车的路径进行优化。汤兆平等[6]利用三角模糊理论和灰色关联理想解解决了不确定应急货物需求的铁路资源调度问题。由此可见不确定因素的影响更为符合实际运输情形，越来越多的学者将其考虑到自己的研究中。

交通业是碳排放的主要来源之一，为构建绿色交通运输体系和践行国家“碳达峰、碳中和”的战略，减碳成为交通部门亟待完成的任务。多年前国外学者就已对减碳进行研究，Demir等[7]考虑出行时间和需求的不确定性，根据温室气体排放目标生成稳健的交通计划，国内交通行业的减碳研究也逐步开展。Lam等[8]建立了碳排放约束下的多式联运集装箱双目标优化模型。国内交通减碳也紧随而至，孙家庆等[9]考虑碳排放限额和碳税税率对碳排放量的影响，从而对冷藏集装箱多式联运的绿色路径进行选择。邱玉琢等[10]构建具有碳排放约束的模型解决生鲜农产品配送车辆路径优化问题。刘倚玮等[11]考虑碳排放成本对多目标集装箱运输组织方式进行优化。在保证了高效运输的同时，兼顾低能耗绿色发展、减少碳排放量是今后主要研究方向。

在多目标运输问题的模型建立和求解方面，邱金红等[12]将变邻域搜索算子融入NSGA-II算法求解多目标车辆路径问题实现了平衡配送收益。徐慧英等[13]通过贪心算法和Or-opt算法改进初始种群和交叉算子后求解多目标车辆路径问题。吴耕锐等[14]引入了贪婪搜索与禁忌表，采用改进的蚁群算法求解城市动态车辆路径优化问题。李凤坤[15]提出改进AHP-GA 算法对多目标配送车辆路径进行优化。Wang等[16]提出了1种扩展精英非支配排序遗传算法来求解双目标优化模型。田旭杨等[17]采用基于约束违反的NSGA-Ⅱ算法解决了城市轨道列车运行多目标模型，并通过不同的度量指标验证算法的优越性。

由上述文献可以发现，现有研究存在4个问题：①对于集装箱海铁联运箱流径路优化问题的研究较少，多集中于车辆路径问题，对于集装箱海铁联运的研究大多没有考虑中转换装的情况，忽略了货源是否充足；②部分文献考虑的是碳经济成本，而非源头减碳量，但目前碳市场和各部门的碳排放量并没有建立直接联系，如此考虑欠妥；③对于多目标问题归一化处理的情况较多，掩盖了解的优越性，容易出现极端值的情况；④国家明确提出形成大宗货物及集装箱中长距离运输以铁路和水路为主的发展格局，应减少公路运输的比例。

笔者以多式联运经营人角度，充分考虑上述问题，综合现有路网研究集装箱海铁联运径路优化问题。首先，考虑运输时间和中转换装时间的波动性，基于运输总费用最少和碳排放量最低建立多目标随机机会约束规划模型，提高运输过程的经济型和环保性。然后，通过改进初始化种群和精英选择算子的NSGA-Ⅱ算法来提高求解速度，考虑货源的充足性，采用算法求解得不同运输组织模式下的运输径路Pareto 解集。最后，通过对比分析和灵敏度分析验证模型和算法在求解径路优化问题时的可靠性和时效性。

1 问题描述

在集装箱海铁联运的实际运输生产过程中，箱流是双向输送的，即箱流遵循铁路运输↔集装箱港站换装↔海洋运输的方式，本文仅选取铁路→海洋方向进行箱流径路的优化研究，运输形式见图1。考虑集装箱运输的实际情况，在不影响模型实效性的前提下做出如下假设。

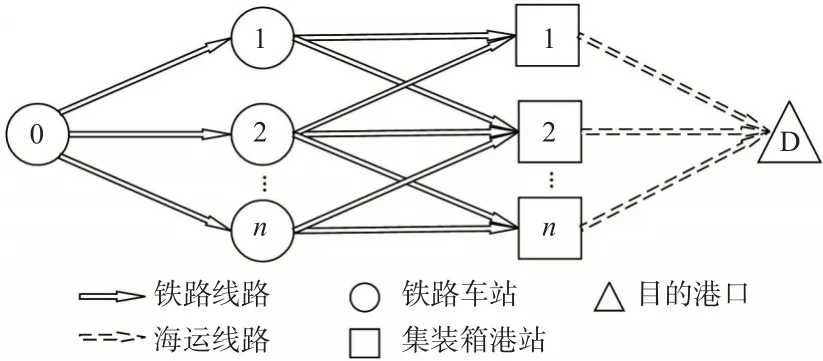
图1 箱流流通方向图Fig.1 Container flow direction diagram

1）始发站的铁路列车数量和集装箱港站的船舶数量充足且每个方向的箱流间互不影响。

2）均采用20 ft标准集装箱开展货物运输，40 ft集装箱可换算为2个20 ft标准箱。

3）考虑到运输效率问题，一站直达式列车选用长编组形式，中转换装式列车选用短编组形式。

4）铁路运输时间和海洋运输时间均为服从正态分布N(μ,σ2)的不确定变量，其中μ为期望值，σ为标准差；集装箱港站的中转换装时间为服从均匀分布U(a,b)的不确定变量，其中a，b分别为中转换装时间的最小值和最大值。

本文拟据此建立随机机会约束规划模型优化箱流运输径路，综合考虑运输时间的波动性，在保证运输费用最低和客户等待成本最小的基础上，致力降低运输过程中的碳排放量。

2 模型构建

2.1 参数及变量定义

1）集合定义。A：铁路车站集合，i,j∈A；E：铁路运输区段集合，(i,j)∈E；L：列车集合，l∈L；M：铁路线路集合，m∈M；H：集装箱港站集合，h∈H；S：船舶集合，s∈S；N：目的港集合，n∈N。

2）运输时间定义。T1/T2/T3：铁路运输总时间/中转换装总时间/海洋运输总时间，h；T运：货物运到期限，h；：列车l从车站i到车站j的运输时间，h；：列车l从车站i到车站j的运输时间的扰动，h，为服从正态分布的不确定变量；t间：列车发车间隔时间，h；：列车l在i站的停站时间，h；：铁路期望运到时间，h；th：集装箱港站h的换装时间，h；：换装时间最大值/最小值，h；ts：船舶s的海洋运输时间，h；t͂s：船舶s的海洋运输时间的扰动，h，为服从正态分布的不确定变量；T2e：海洋期望运到时间，h。

3）载运通过能力定义。Ci：车站i接发列车的能力，列/d；Cij：i-j区段的通过能力，列/d；Ch：集装箱港站h的换装能力，TEU/d；Cc：集装箱港站h的存储能力，TEU；Cs：船舶s的载运能力，TEU/艘。

4）相关变量定义。c1：单趟列车l的固定使用成本，$/列；c2：列车l运输单位集装箱货物运行单位公里的费用，$/TEU·km；：铁路i-j区段运输距离，km；ql：列车l在线路m上运送的集装箱数，TEU；c3：换装机械及换装工人单位时间中转换装费用，$/h；：铁路线路m运输到集装箱港站h的箱流量，TEU；η：中转换装效率，TEU/h；c4：货物在集装箱港站的存储管理费用，$/TEU；c5：海运包箱费率，$/TEU·km；：集装箱港站h中转换装的箱流量，TEU；：集装箱港站h到目的港n的海运距离，km；ys：使用船舶s需支付的船体使用费及折损费，$/艘；ζ：客户等待时间折算成本，$/TEU·h；Qn：目的港n需要的货物箱数，TEU；λ1：1 kWh 电等于的碳排放量，取为0.96 kg；λ2：1 kg 油等于的碳排放量，取为3.15 kg；ϕ：电力机车每吨公里耗电量，kW·h/t·km；μ：船舶每吨公里耗油量，kg/t·km；Kij：不同区段电力机车的单耗系数，取值范围[0.7，1.3]，Kij越大说明线路条件越差，电力机车能耗也就越大；：列车l/船舶s运送的货物吨数，t；：列车l的编组辆数，节/列；：全天内 列车l在i站停站/通过的频次，次/天；Nm：线路m上的车站总数量，个。

5）0-1 变量定义。xl：是否使用列车l运输货物，使用取1，否则取0；xh：货物是否在集装箱港站h进行换装，换装取1，否则取0；xs：是否使用船舶s将集装箱从港站h输送至目的港n，使用取1，否则取0；：列车l是否经过i-j区段，经过取1，否则取0；xil：列车l是否经停i站，经停取1，否则取0。

2.2 模型目标函数

采用随机规划建立随机机会约束规划模型。目标1以最小化运输费用和客户等待成本为目标。其中运输费用包括铁路运输费用、中转换装费用和海洋运输费用，见式（1）～（3），客户等待成本见式（4）。

故目标1为

目标2以运输过程中铁路机车消耗的电能和海运船舶的燃油最少为目标，进行单位统一化处理，等同转化为相应的碳排放量，以达到节约资源、保护环境的目的，此目标弥补了众多现有研究未考虑源头减碳量的缺陷。

2.3 模型约束条件

1）不确定时间约束。采用随机约束和区间非线性规划这2 种方法描述不确定时间，避免单一方法的局限性。式（7）表示中转换装式列车铁路运输时间的不确定约束，即铁路运输固定时间、运输波动时间、停站时间和列车发车间隔时间之和要以α的概率大于等于铁路期望运到时间，若为一站直达式列车则停站时间取为0；式（8）表示集装箱港站中转换装时间处于换装时间的最小值和最大值之间；式（9）为海洋运输时间的不确定分布，固定运输时间和运输波动时间之和要以γ的概率大于等于海洋期望运到时间。

2）集装箱流量守恒约束。在铁路列车输送到集装箱港站的箱流量中，换装部分为目的港口的需求量，即需要装船运输的箱流量，剩余箱则在集装箱港站进行储存，保证整个运输过程中的箱流量守恒。

3）径路唯一性约束。式（13）～（15）说明铁路列车从始发站到终点站径路通畅且唯一。

4）能力约束。兼顾各种能力约束，式（16）～（19）分别为铁路区段通过能力约束、集装箱港站换装和存储能力约束、船舶载运能力约束、铁路车站接发列车能力约束。

5）其他约束。式（20）表示货物只有通过铁路运输后才能在集装箱港站进行换装，若换装则必然进行海洋运输；式（21）表示所选用货物列车始发站和终点站必须停靠；式（22）为0-1约束。

3 模型转化

第2节给出不确定环境下集装箱海铁联运径路优化的运输组织模型，下面则需要利用相关不确定理论知识将随机运输时间和中转换装时间约束进行确定转化，并对超过铁路运到期望和海洋运到期望的相关路径的目标函数进行惩罚处理，则可得最终运输模型。

3.1 不确定理论相关定义

定义1。不确定变量的不确定分布Φ 定义为其中，x为任意实数。它的反函数为不确定分布的逆分布，记为

定义2。当且置信水平α∈（0,1）时，假设ξ是1个服从连续不确定分布Φ(x)的不确定变量。那么当且仅当成立，其中

定义3。正态分布的不确定分布函数为其逆函数为

定义4。若，则

定义5。对于区间Ψ 中的任意值th∈Ψ，定义时间影响系数通过变换可得

3.2 确定模型转换

由于正态分布具有集中性、对称性和均匀变动性等优良特性，文献[21]规定不确定运输时间服从正态分布，即由定义4可得：

利用定义1～5将不确定模型中的式（7）～（9）进行如下线性转换以方便求解。

3.3 目标函数处理

因有些路径的运输时间超过铁路或海洋期望运输时间，故在目标函数中加入惩罚函数进行处理，保证输送径路的优越性。方法见式（28）。

经惩罚处理后可将式（1）和式（3）修改为

经过以上环节的确定转换及惩罚处理，则可把不确定环境下的随机机会约束规划模型转为线性可求解形式。最终可得确定模型的目标函数为式（5）、式（6），约束条件为式（10）～（22）、式（24）～（25）、式（27）。

4 模型求解算法

NSGA-Ⅱ是Deb于2000年提出的[23]，其采用快速非支配排序，拥挤度和拥挤距离以及精英选择策略来提高求解速度，保证优化结果解的精度，是求解多目标优化问题的有力工具。本文求解算法流程图见图2。

图2 算法流程图Fig.2 Algorithm flow chart

由于传统NSGA-Ⅱ算法对初始种群依赖性大且容易出现提前收敛以及局部最优的状况，故本文参照文献[13]对传统NSGA-Ⅱ算法的初始化种群进行改进。同时参照文献[17]对传统NSGA-Ⅱ算法的精英选择算子进行改进，提高算法性能后求解本文站点数为19 的集装箱海铁联运径路优化问题。部分求解过程如下。

步骤1。初始化种群改进。传统的NSGA-II 只是保证产生的路径通畅且货运量满足需求，但其对初始种群依赖性较大，因此引入贪心算法，即局部最优思想对初始化种群进行改进。

首先随机产生初始染色体片段，然后基于贪心思想，为初始染色体的最后1 个基因位产生后续基因。具体做法是建立1 个距离矩阵,参照矩阵为初始染色体片段的最后1个结点寻找距离最短的结点将其作为后续结点，该结点要满足未出现在染色体中，如此重复，直到染色体的最后1个基因位为目的站点。

步骤2。精英选择算子改进。NSGA-Ⅱ常采用的选择策略是二元锦标赛法。通过随机挑选种群的个体进行两两比较，选择较为优秀的个体存入到交配池中，本质上为放回抽样。有放回的选择极易产生许多重复个体，导致解集分布均匀性较差，容易出现提前收敛或局部最优的情况。

为解决该问题，本文使用1种基于logistics分布的概率选择算子。如果个体X1优于X2，在种群进化初期，则以较高的概率放弃优胜个体X1，转而选择劣势个体X2，保证了算法初期的种群多样性；进化后期，由于解集逐步收敛，此时以较大的概率选择X1，使得种群加速收敛，选择X2的小概率可能也同时得到保留。选择非支配解概率计算公式为Pselect=其中θ为概率选择经验参数，gn为当前迭代次数。

步骤3。交叉和变异。对染色体采用2 点交叉法，随机设置2个交叉点，交换2个个体在所设定的2个交叉点之间的部分染色体，由于交叉后可能导致路径不同从而得到无效的子代染色体，因此需要对无效的子代染色体进行处理。

1）若父代1（父代2）交叉片段中有与父代2（父代1）非交叉片段路径有重复的节点，则交叉后删除重复部分即可，见图3。

图3 交叉示意图1 Fig.3 Cross diagram 1

2）若交叉后路径不通，则需要补充一部分节点使路径通畅，见图4。交叉后节点7和节点11是不直接连通的，因此需要补上中间路径节点10，中间路径节点的补充是随机的，这样也保证了种群的多样性。

变异操作能够保证种群的多样性，避免过早收敛。通过随机选取1 个路径片段进行替换，得到新的染色体，见图5。

图5 变异示意图Fig.5 Variation diagram

5 案例分析

5.1 案例描述及初始数据设定

本文以西安至洛杉矶港输送特定数量的集装箱货物为运输背景进行案例分析。考虑到运输的时效性，在始发站货源充足的情况下选用编组辆数为60的一站直达式长列编组列车，在货源不足的情况下选用编组辆数为40 的中转换装式短列编组列车。根据各地经济发展水平以及车站规模大小，中转换装的车站取为太原、郑州、济南、徐州、武汉、南京6站。每辆车可装2 个20 ft 标准集装箱，列车运行速度取为100 km/h。列车发车间隔和大站停车时间分别取为30 min和45 min。铁路和海洋不确定运输时间扰动的标准差取值范围分别为随机选取标准差生成每1 个区段的不确定运输时间扰动，置信水平α,γ∈[0 ,1] 。中转换装时间影响系数β∈[0 ,1] ，变化β的取值生成不同的中转换装时间。

考虑到多式联运经营人交接、报关报检、订舱等代理业务，以及不同运载工具的装卸时间等，中转换装时间取为[50 h，60 h]。船舶类型可供选择，见表1。假设目的港洛杉矶港所需集装箱数量为3 200 TEU，货物运到期限为485 h。通过官方网站及文献研究得铁路车站区间里程、电力机车单耗系数、铁路区间通过能力、车站接发列车能力及海运距离等数据见图6（运输线路示意图）。集装箱港站换装及存储能力见表2，相关数据说明见表3。

表3 相关参数说明表Tab.3 Description of relevant parameters

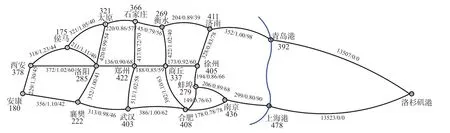
图6 西安至洛杉矶港运输线路示意图Fig.6 Schematic diagram of transportation route from Xi'an to LosAngeles port

表2 集装箱港站换装存储能力表Tab.2 Table of container port station reloading storage capacity

5.2 运行结果分析

在Win10-64位的系统环境下使用Matlab 2018b软件运行求解，其中种群大小设为100，最大迭代次数为500次，交叉概率取为0.7，变异概率取为0.1，初始置信水平α取为0.85，γ取为0.8，时间影响系数β为1。迭代运行可得不确定环境下一站直达模式（货源充足）和中转换装模式（货源不足）的Pareto解集，见表4。

表4 运输方案Pareto 解集Tab.4 The pareto solution set of transportation scheme

一站直达模式下方案1可满足较低的运输总费用，而方案2 则可以实现更低的碳排放量。同理对于中转换装模式下，方案3/6的运输总费用低于方案4/5的运输总费用，但其碳排放量却显著升高。同时方案3/6的货物送达准率要明显优于方案4/5。因此可根据运输部门对运输总费用和碳排放量的侧重点以及收货人对货物送达准点率的要求灵活选择径路，体现出Pareto解集的优越性。

5.3 对比分析

1）算法优化前后对比分析。将本文改进后的NSGA-Ⅱ算法与未改进的NSGA-Ⅱ算法进行对比，绘制算法优化前后各个子目标最优解的收敛情况图，见图7～8。由图7可见：运输总费用改进之前收敛代数在300代左右，这是由于初始解集质量较差，而改进后大概75 代就收敛，初始解集质量优越，收敛代数的减小表现出改进算法后求解的高效性。同时改进算法的前沿曲线更加平滑，这是因为传统NSGA-Ⅱ算法对初始种群依赖程度大，引入贪心算法改进初始化种群后初始种群随机性降低，同时通过精英选择算子改进使得种群的多样性得以保留。同样由图8 可见：碳排放量改进之后也在75 代左右收敛，在迭代初期由于种群的随机性和多样性使碳排放量迅速降低继而快速增加，随着迭代次数的增加种群个体逐渐趋于优秀直至收敛值。改进算法的前沿曲线在75代左右不再更新，说明改进算法在提高求解效率的同时还能保持稳定性，不影响最优解的质量。

图7 运输总费用收敛情况比较Fig.7 Comparison of total transportation cost convergence

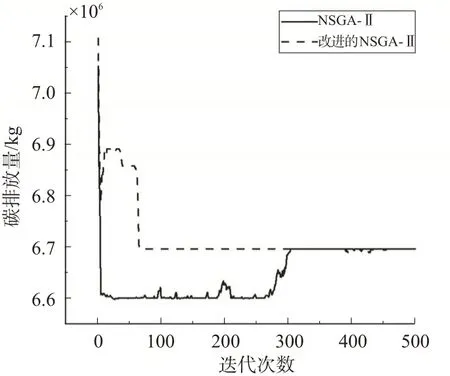
图8 碳排放量收敛情况比较Fig.8 Comparison of carbon emissions convergence

1）固定相关参数，对改进前后的NSGA-Ⅱ算法分别运行10 次，运行结果见表5。由表5 可见：算法改进后，运输总费用和碳排放量2 个目标值都有不同程度的降低，减少运输总费用231 458.73$、碳排放66 887.32 kg，提高了经济性和环保性。同时收敛代数被明显优化，较改进前优化了75.36%。因此改进初始化种群和精英选择算子的NSGA-Ⅱ算法能在显著提高求解速度的同时，还避免了传统算法容易陷入局部最优的状况，保证最优解的质量。

表5 算法改进前后结果对比分析Tab.5 Comparative analysis of results before and after algorithm improvement

3）确定环境和不确定环境对比分析。取铁路、海运波动时间为0，中转换装时间固定为55 h，对比确定环境和不确定环境的运输总费用以及货物送达准点率，见表6。一站直达模式下，确定环境和不确定环境下的运输总费用相差不大，货物送达准点率均达到100%。中转换装模式下，某些路径在不确定环境下的运输总费用有相应提升，货物送达准点率也适当降低，费用相对偏差也较大，这与运输时间和中转换装时间的波动有关。即运输总时间越长，货物的送达准点率也就越低，同时伴随着惩罚费用和客户等待成本的加入造成了运输总费用的提升。运输时间在现实状况中会受各种不确定因素的影响，为保证运输效率和运营效益，其波动性是不容忽视的。

表6 确定环境和不确定环境的对比分析Tab.6 Comparative analysis of deterministic and uncertain environments

4）单目标和多目标对比分析。对中转换装模式下进行单目标和多目标对比分析，见图9。分别以运输总费用最低和碳排放量最少为目标进行求解，得方案3 的运输总费用最低，但其碳排放量最多，相对于最少碳排放量的方案高出1.76%；方案5与方案3 相反，其碳排放量最少，运输总费用却最高，比最低运输费用方案高出4.54%。而改进NSGA-Ⅱ算法求解的Pareto 解集中有方案4 和方案6的各个子目标值都介于二者之间，显然更受现实选择的倾向。不难发现，单目标模型很难使2 个子目标同时达到最优值，其中1 个子目标性能的提升必然会导致另1 个子目标的降低，多目标优化则可以对多个目标进行权衡和折衷，使各目标尽可能实现最优。

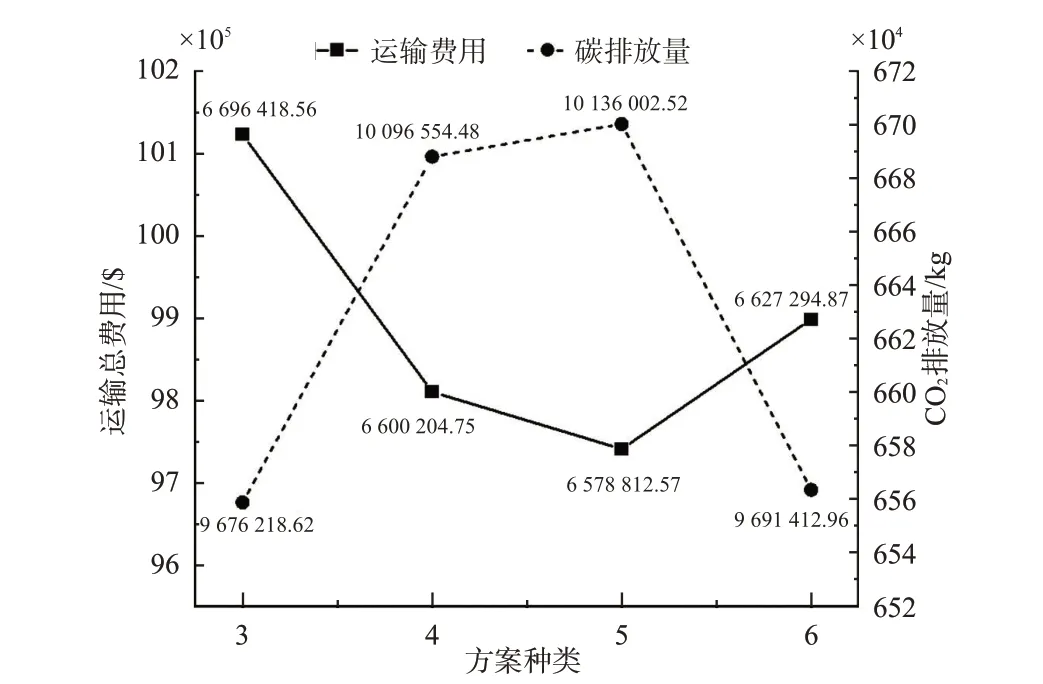
图9 单双目标对比分析Fig.9 Comparative analysis of single and dual targets

5）随机约束规划和模糊约束规划对比分析。采用梯形模糊数对铁路和海洋不确定运输时间进行表示，将随机机会约束转化为模糊机会约束后求解，与随机机会约束对比分析，结果见表7。中转换转时间均取为55 h，其中梯形模糊变量由清晰数构成的四元组(a,b,c,d)表示，a≤b≤c≤d。由表7 可见：随机约束规划的运输方案Pareto解集比模糊约束规划多2个，且相对应方案的运输总费用较模糊约束规划都低，均优化了10.65%，同时随机机会规划最优解集的运输船舶类型为船舶3，模糊约束规划的为船舶1。随机约束规划更能实现对解集的遍历，找出更多符合运输条件的解，为运输部门和收货人提供路径选择的便利。

表7 随机规划与模糊规划对比分析Tab.7 Comparison analysis of stochastic planning and fuzzy planning

5.4 灵敏度分析

由于一站直达式列车中途不进行停站装卸货物，只有集装箱港站换装时间和途中运输时间，故总的运输时间短，在置信度较高的水平下仍能充分满足铁路运输和海洋运输的期望时间，在货物规定的运到期限内送达。所以参数的改变对一站直达式运输方式带来的变化并不显著，故在此分析置信水平α和γ以及时间影响系数β的改变对中转换装式运输方式产生的影响。船舶类型固定为船舶3，运输径路取为西安-洛阳-郑州-商丘-徐州-济南-青岛港-洛杉矶港。

1）置信水平α和γ对运输总费用的影响。取α变化范围为[0.65，0.95]，γ为[0.6，0.9]，绘制运输费用图，见图10。图中分析可知随着置信水平的增大运输总费用呈现上升的趋势。这说明货物要求在铁路、海洋期望运到时间内运到的概率越高，则相应的运输费用也就越高，此时延误率大的解将不会被采纳，体现出模型和算法的正确性与合理性。

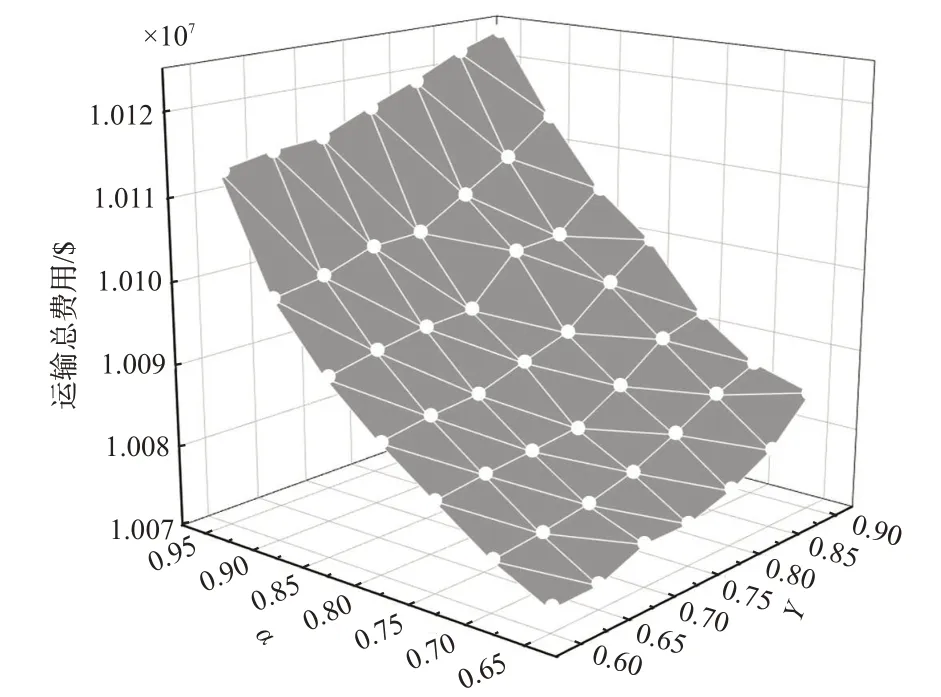
图10 不同置信水平下的运输费用图Fig.10 Transportation cost under different confidence levels

2）中转换装时间影响系数β对货物送达准点率的影响。固定置信水平α=0.85，γ=0.8，铁路运输和海洋运输波动时间取为0。扩大中转换装时间影响系数β变化范围，取为[0.6，1.8]，增长步长取为0.2，观察其对货物送达准点率的影响，见图11。分析可知时间影响系数和货物送达准点率呈负相关，影响系数越大货物送达准点率越低。即加快集装箱港站的换装效率是提高货物送达准的重要措施之一。

图11 时间影响系数对货物送达准点率的影响Fig.11 Influence of time influence coefficient on on-time delivery of goods

6 结束语

本文基于多式联运经营人角度，兼顾交通运输业的碳减排任务以及国家“公转铁”的倡导，以集装箱海铁联运在实际运输过程中受到的不确定运输时间和中转换装时间为出发点，建立多目标随机机会约束规划模型优化海铁联运箱流径路。带入实际运输网络进行核验运算，多角度对比分析验证模型和算法的稳定性和优越性。

1）初始化种群和精英选择算子的改进降低了运输总费用和碳排放量，同时也提高了算法的求解速度。由于时间的波动性，不确定环境下的运输总费用较确定环境下高，货物送达准点率相对降低，中转换装模式下效果更为显著，但实际运输过程中存在诸多不确定因素的影响，不容忽视。多目标规划比单目标规划更为符合现实情况，能够使各目标综合实现最优。随机机会约束规划解集中解的数量多于模糊机会约束规划，且运输总费用更低，为运输部门和收货人提供多种选择。

2）灵敏度分析置信水平对运输总费用的影响以及中转换装时间影响系数对货物送达准点率的影响。结果表明：要求准点送达的概率越大则相应的运输费用越高，时间影响系数越大，货物送达的准点率越低，符合运输实际，验证模型和算法求解运输径路问题的正确性。

本文研究的运输情景基于单一发送地和单一目的地，但多个OD 间的运输径路优化更符合当前运输实际，也是后续应该致力于研究的方向。同时考虑包括生产端和应用端的全生命周期碳排放量更加有助于双碳目标的达成，其具体核算方法也是后续应研究的方向。