基于虚拟仿真的圆波导教学方法

骆新江， 张鹏泉， 张忠海

（杭州电子科技大学电子信息学院，杭州 310018）

0 引 言

随着无线技术的发展，电磁场与电磁波技术的应用越来越广泛。与矩形波导相比，圆波导由于其较高的几何对称性，机加工方便，误差小；相同横截面周长的圆波导比矩形波导衰减小，功率容量大，品质因子高［1］。大多数传输线随频率的升高，衰减也会随之增加，而圆波导中的TE01模，随着频率的升高衰减反而降低［1］。根据圆波导的这些特点，它常常被做成各种器件，应用在多种场合，例如，旋转关节［2］，波导天线［3］、模式转换器［4］、功率分配器／合成器［5］、滤波器［6］、移相器［7］、振荡器［8］和开关［9］等。掌握好圆波导中电磁波的行为特点，对今后开发市场需求的圆波导器件至关重要。在学习圆波导相关理论时会遇到柱坐标系和一些特殊函数，学习起来比较抽象，难理解。多数教科书中都是采用理论推导的方法，烦琐的数学过程不仅使学生望而却步，还易产生本末倒置的错觉。对于电子信息类专业的学生，求解方程的过程并不是重点，应将更多精力放在解题的思路和理解上来。随着优秀的数学仿真软件（如Wolfram Mathematic，Matlab，Maple）和电磁场仿真软件（High frequency simulation software，HFSS），CST（Studio Suite，FEKO）的出现，不仅为电磁场与电磁波工程设计提供了辅助工具，同样为电磁场与电磁波的教学改革提供了可能。目前在这方面已经涌现了一批优秀的教学案例［10-16］。这些案例的成功为圆波导教学方法改革提供了经验。

1 理论解析

圆波导具有柱对称性，采用柱坐标系求解场结构，如图1所示。圆波导是单导体传输线，只能传播横磁Transverse magnetic（TM）波和横电Transverse electric（TE）波，不能传输横电磁波TEM［1］。对于这种电磁波场的解题思路如图2所示。一切电磁现象的基石都是麦克斯韦方程。对于电磁波而言即为无源的麦克斯韦方程。对方程组中电场和磁场去耦合可得波动方程。对于圆波导中的电磁场分布，可先求纵向场分布，利用变换矩阵求解横向场分布。

图1 圆波导及坐标系

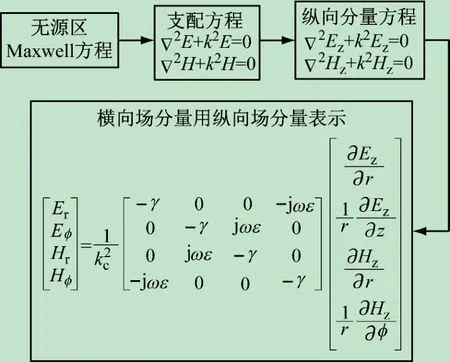
图2 圆波导横向场分量解题思路

在图1所示的柱坐标系下，z轴为波传播方向，即纵向，ρ和φ为横向。对于TE波，Ez＝0，Hz满足∇2Hz＋k2Hz＝0，Hz是关于变量ρ、φ和z的函数。可设Hz＝R（ρ）Φ（φ）Z（z），利用分立变量法可分别求得：

式中：c、c1、c2、c3、c4为系数；m＝0，1，…为整数；γ为传播常数；k为波数；kc为截止波数；Jm（kcρ）为第1类m阶Bessel函数；Nm（kcρ）为第2类m阶Bessel，即Neumann函数。式（1）中后一种书写法更紧凑直观地表现了两种函数“或”的关系。文章后面关于各种场结构的解析式均采用这种方法，它能够直观地看出场结构中的角度简并模式。

学生对这类特殊函数并不熟悉，在课堂教学环节中必须插入Bessel函数和Neumann函数的相关知识，否则学生很难理解后面的求解结果。在Mathematica软件中输入如下命令：

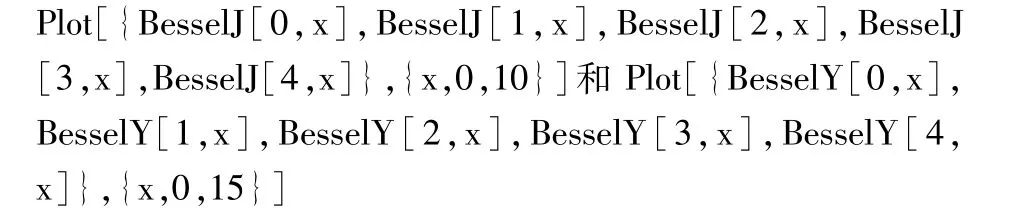
及刻画出0～4阶的Bessel函数和Neumann函数图形，如图3（a）、（b）所示。

图3 0～4阶的Bessel函数和Neumann函数图

从图3（b）Neumann函数图形，可以发现在自变量趋于0时，函数值趋于无穷大，而由有限边界条件可知，解中不会出现Neumann函数。所以纵向解只能为

将式（2）Hz中的求解结果和Ez＝0一并代入图2求横向场的矩阵方程中，结合边界条件即可解出横向场分布，这里需用到的边界条件有：①有限边界条件f（ρ＝0）≠∞；②周期边界条件f（φ＝0）＝f（φ＝2π）；③理想导体边界条件Et（ρ＝a）＝0。其中t为切向分量，这里具体为Eφ＝0，Ez＝0。

对于理想导体和理想电介质的情况，TE模的所有场分布结果列于式（3a）上面。同理可得TM模的场分布，列于式（3a）下面。利用对偶关系也可得出同样的结果（式3（b））。将TE和TM模的电磁场分布一同列于式（3），更容易通过对比发现其中的规律。式中，μmn为TE模第1类m阶Bessel函数导数的第n个根，即J/

m（kca）＝0，此时

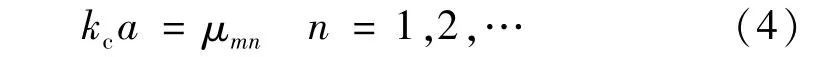
υmn是TM模第1类m阶Bessel函数的第n个根，即Jm（kca）＝0，此时

由式（4）可知，TE模的截止波长

由式（5）可知，TM模的截止波长

可见，当m和n取不同数值时，μmn、υmn和截止波长也取不同数值。这种对应关系见表1。将表1中各模式的截止波长按从小到大的顺序排列成数轴形式更容易发现其中的规律，如图4所示。

表1 m和n取不同数值时μmn和υmn的值和对应的截止波长

图4 圆波导中不同模式电磁波的截止波长与传播区域数轴图

由图4可见，截止区对应的波长下限为3.41a，以及各模式的工作波长区间和兼并情况。但无法观察到另外一种兼并模式，即角度兼并，当角度旋转90°时sin（mφ）和cos（mφ）就会相互转换。这点解析结果中已经给出，但却不够形象。在仿真分析部分将各种场结构可视化后，展示了这种兼并形式。这里需要特别强调的是，圆波导中的模式指数m和n同矩形波导中的物理含义是不一样的。为便于区别和理解，将这两种情况列于表2。由于J/0＝－J1，所以TM1n模和TE0n模的截止波长相等，发生简并。但相同的m和n值，μmn和υmn不相等，TMmn和TEmn的截止波长就不会相等，所以这两种模式不会发生简并。

表2 圆波导和矩形波导中模式指数m和n的含义

2 仿真分析

采用标准圆波导BY40对上述推导的结论进行仿真。标准圆波导BY40的腔体内半径a＝25.995 mm，按照图1结构在HFSS软件环境下建立电磁仿真模型。过程如下：①建立波导结构；②设定材料属性，导体设为理想金属，内部介质为真空；③设置端口激励以及阻抗积分线；④设置网格基准频率，这里设置为10 GHz；⑤扫频仿真，这里取1～10 GHz；⑥观察仿真结果。不同频率下的插损仿真结果如图5所示。

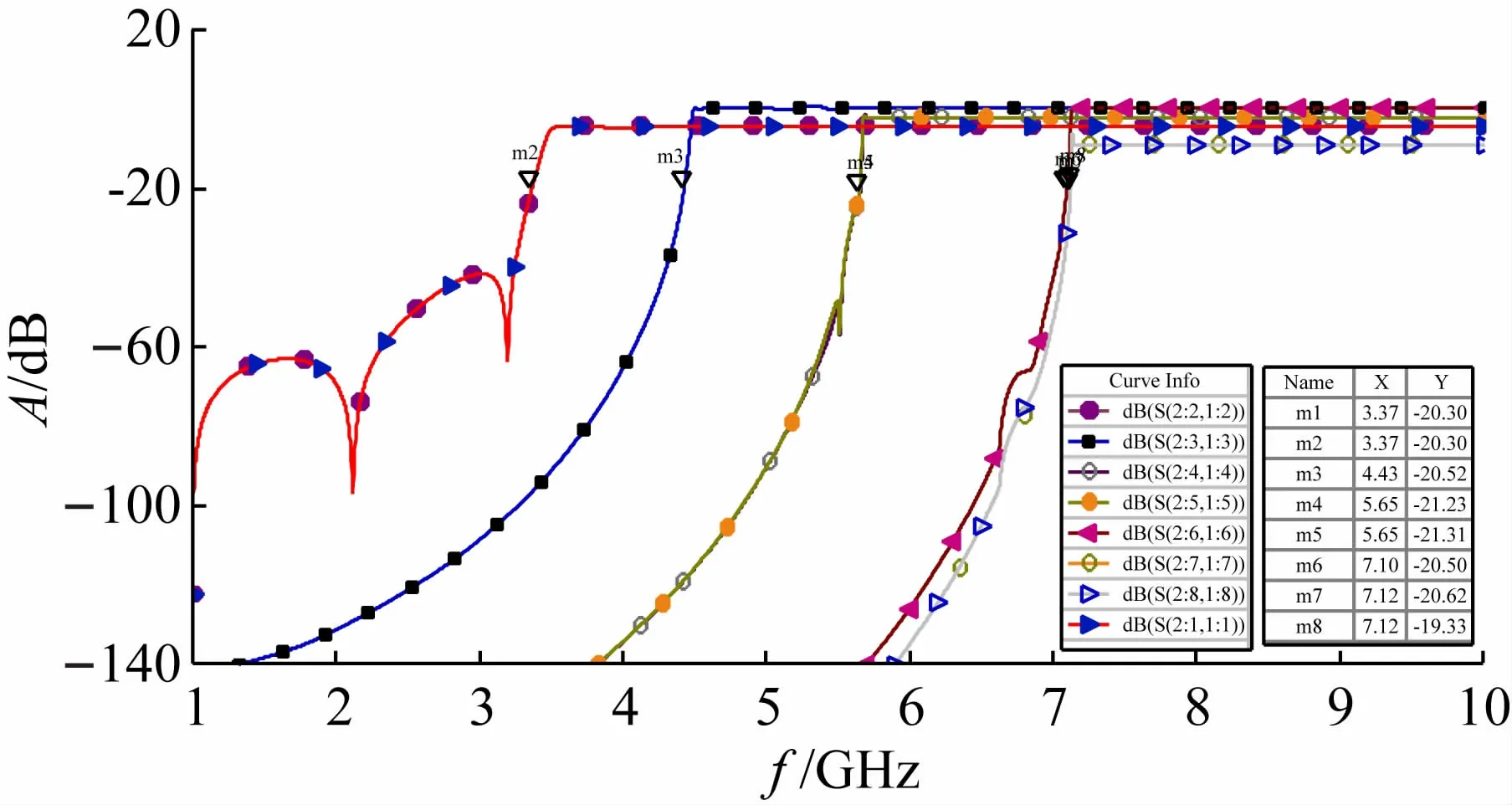
图5 不同模式下插损仿真值

通常认为传输能量低于1%（－20 dB）时即为截止。将－20 dB的标号放于各模式的插损仿真曲线上，其对应的频率即为截止频率。与GB 11450.4-1989中BY40中标准数据对比结果列于表3。通过对比可发现误差很小，因此仿真结果是可信的。

表3 各模式电磁波截止频率

由图5、表3可见，标号m1、m2，m4、m5，m7、m8对应曲线和数据相重合，进一步证明了存在简并模式。各标号对应的解析式与场结构仿真图，如图6～10所示。各图中共分两栏左电场侧解析式对应左侧电场结构，右侧磁场解析式对应右侧磁场结构。场结构的分布和兼并情况从图中一目了然。

图6 TE11模式场结构分布图

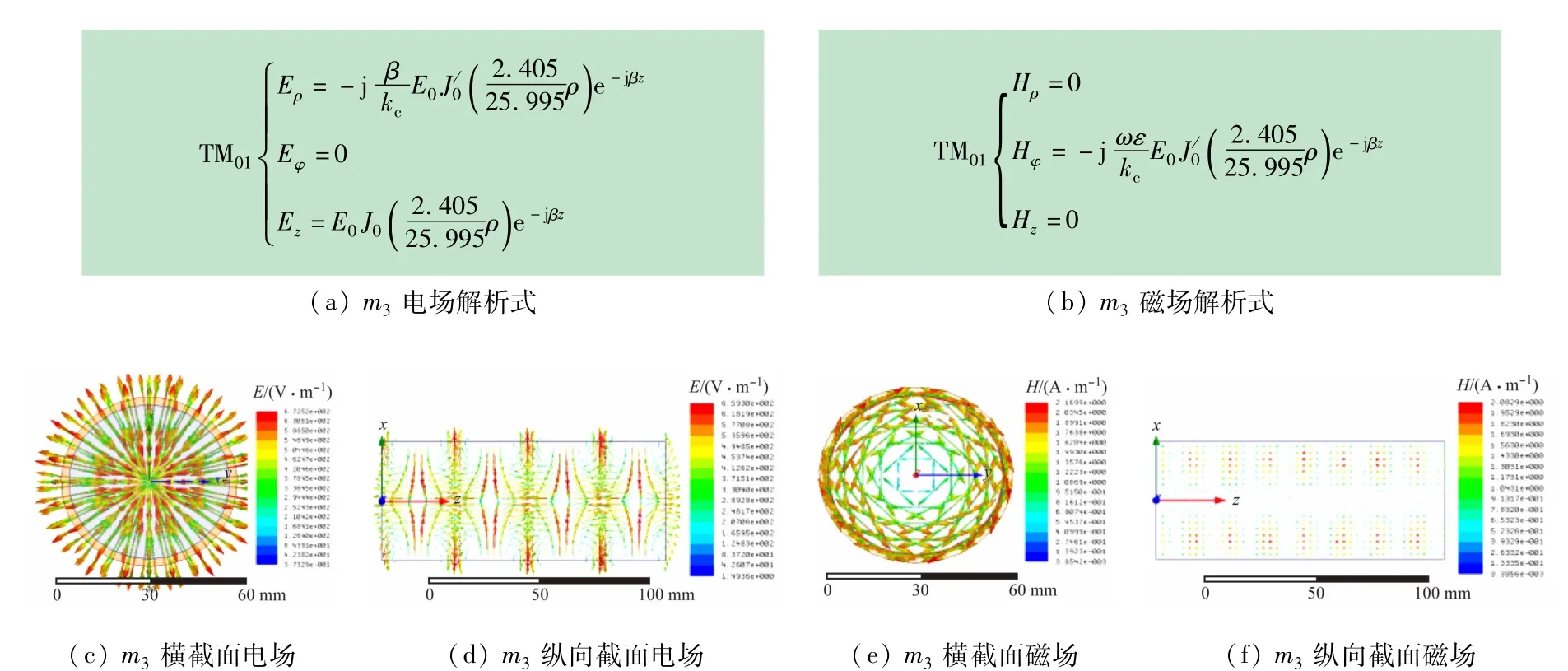
图7 TM01模式场结构分布图

由以上场结构解析式和仿真图不难看出，各模式场结构分布情况与数学解析式是相吻合的。场结构可视化结果形象的展示了场模式指数的物理含义，同时也能观察出角度兼并的存在，如在TE11模，TE21模和TM11模中都发生了角度兼并。另外，对未知的场模式，结合指数的物理含义，从场结构仿真图很容易知道波导中传播的是何种场模式。

图8 TE21模式场结构分布图

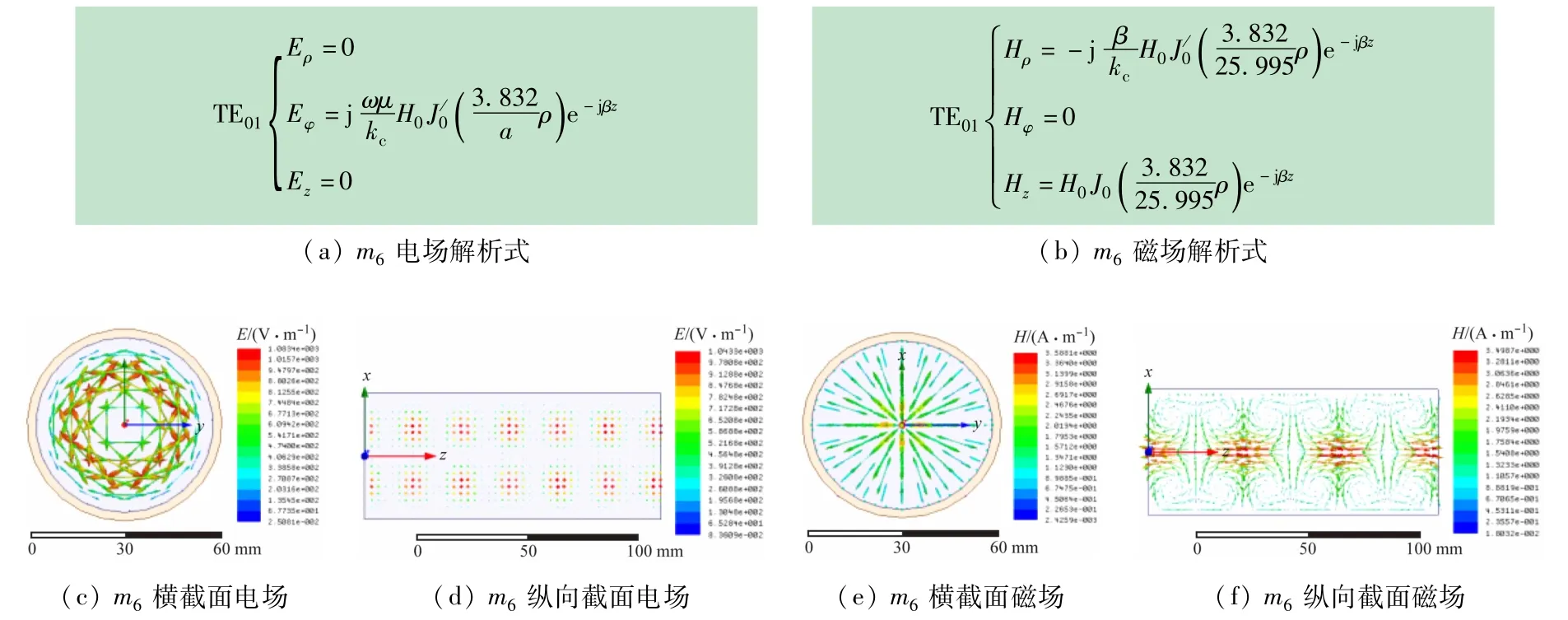
图9 TE01模式场结构分布图

图10 TM11模式场结构分布图

3 结 语

提出圆波导场结构的求解思路，对比列出圆波导中TM波和TE波的场结构结果。以标准圆波导BY40为例，利用HFSS仿真软件对传输特性，场结构分布进行了仿真分析。仿真结果与理论分析完全吻合。这种基于可视化的仿真辅助教学可以很好的理解圆波导中电磁场的传播特点。