基于神经网络的电网潮流图自动拓扑布线方法

徐遐龄，田国辉，刘 涛，于文娟，肖大军，梁陕鹏

（1. 国家电网公司华中分部华中电力调控分中心,湖北省 武汉市 430077；2. 南瑞集团有限公司（国网电力科学研究院有限公司）,江苏省 南京市 211106；3. 北京科东电力控制系统有限责任公司,北京市 100192）

0 引言

电网潮流图主要由厂站、线路、工况信息等元素组成,用于实时反映电力系统的运行状态,电力系统调度人员通常用电网潮流图实时监视电网的潮流分布。潮流图人工制作十分费时,其自动生成的工程实践一直在探索进行中。

近年来已有许多电网接线图自动生成方面的研究,输电网自动成图方面,文献［1］通过模拟退火算法生成厂站的画面坐标位置,然后通过坐标的数学计算方式计算出首、末端厂站的相对位置和方向,再进行直连线、双折线、四折线等形式的自动线路连接生成潮流图；文献［2］提出基于变电站经纬度坐标,首先进行离散化布图和拓扑简化实现变电站的初始布局,再结合改进的模拟退火算法进行优化布局,最后对变电站之间采用直线连接实现自动成图。文献［1-2］所述方法生成的连线样式比较固定,无法灵活根据厂站布局处理复杂多样的线路交叉、重叠、绕障等问题。文献［3］提出了一种线路的走线避让算法,可解决部分线路的绕障交叉问题；文献［4］进一步提出在线路顺序走线基础上通过拆线重布和整体均匀布线对初始走线进行整体优化,从而减少交叉点；文献［5］提出采用A 星算法对输电线路进行线路规划,成图之后再对线路的布局进行微调。文献［3-5］算法可以整体提高线路的拓扑质量,但是这些算法都是针对画面线路特征人为地进行优化,实际应用中碰到的问题要复杂得多,线路长度、交叉点数、分布密度等特征往往是互斥的,每个算法只能单一解决某类问题,当多个问题叠加时此类算法无法智能地自主选择并权衡,因此无法兼顾不同线路特征进行拓扑布线。随着电力系统越来越复杂,不同地区和应用场景对潮流图的展示有差异化需求,上述方法在自动成图时需要针对不同的成图要求人为适配不同的算法来实现定制化的半自动成图,这将大大降低自动成图的可用性和灵活性。在配电网自动成图方面［6-9］,文献［6］提出通过构建基于迭代二叉树3 代（ID3）算法的决策树机器学习模型,采用配电网数据为训练样本进行机器学习来提取画面布局特征完成自动成图；电网厂站接线图自动成图方面,文献［10］提出基于对电力系统图形描述规范CIM/G 的拓扑分析,对存量图形进行特征识别与特征提取,利用图形特征实现厂站接线图的自动生成。文献［6,10］通过机器学习提取画面图形特征实现自动成图,与传统自动成图算法相比,不依赖具体的坐标计算,具有更好的灵活性和通用性。但是基于高质量的人工画面样本进行学习,需要有足够数量的数据样本作为支撑,而电网潮流图训练样本相对较少,电网系统内各地方的图元规模和拓扑特点存在差异,目前还没有针对潮流图形成一个全国统一的图形特征库,限制了学习的样本空间。同时,由于潮流图的拓扑特征与配电网以及厂站的接线图存在差异,配电网和厂站自动成图并不完全适合应用于电网潮流图的自动成图。

针对现有自动成图的问题和现状,本文提出一种基于神经网络的自动线路布线方法,基于此方法结合电网厂站和线路模型实现自动生成电网潮流图。本文方法构建了一个关联线路步长方向选择和线路质量的神经网络,通过神经网络的训练获取路径规划策略来实现自动拓扑成图。

1 厂站布局

1.1 基于图元拓扑深度和广度计算厂站布局区域

厂站图元的拓扑值计算示例如图1 所示。

图1 厂站图元的拓扑值计算Fig.1 Calculation of topological value of plant and station elements

图元的拓扑深度指的是图元最多有几层子节点,例如：图1 中图元“4”的最深遍历路径是4→10→15→16→22 共5 级,因此图元“4”的拓扑深度是5。图元的拓扑广度指的是图元的第1 级子节点的总个数,例如图元“1”有2、4、3、5 这4 个子节点,因此图元“1”的拓扑广度为4。

把潮流图画面由内向外逐级分层（从画面中心到画面边缘逐级分层,如图1 中由内向外分别对应布局图层1、布局图层2、布局图层3 和布局图层4）,将拓扑关系复杂度最高的图元作为潮流图的中心厂站布局到中心图层,然后以中心厂站为核心向叶子节点逐层布局。拓扑关系的复杂度通过拓扑深度和广度的计算获得,设定拓扑复杂度等于厂站的所有一级子节点的拓扑深度之和。图1 中,厂站图元“1”的4 个叶子节点2、4、3、5 的最大拓扑深度分别是3、4、3、5,所以图元“1”的拓扑复杂度为3+4+3+5=15。根据拓扑信息依次计算出每个图元的拓扑复杂度,最后找出拓扑复杂度最大的厂站图元节点,将此节点放入中心图层,即图1 中的“布局图层1”,然后将中心厂站的一级节点放入“布局图层2”,以此类推逐级向外布局,拓扑复杂度取值越低,则越靠近外部布局图层。

1.2 厂站布局区域内位置定位

每个厂站图元根据自身拓扑复杂度取值找到对应的布局图层后,就确定了图元的布局范围,下一步需要确定厂站图元在布局图层内的具体坐标。

每个布局图层按垂直和水平方向被平均划分为4 个象限,以图1 中“布局图层2”为例,“布局图层2”内的厂站图元相对父节点1 存在“右上”“右下”“左下”“左上”4 个方位,4 个方位分别对应布局图层的第1、第2、第3、第4 象限。厂站图元布局时应保证自身相对父节点的方位合理,即计算图元应布局在图层内的哪个象限。厂站图元相对父节点的方位通过厂站的经纬度计算获得,通过厂站和父节点厂站的经纬度对比可以确定自身位于父节点的方向,从而确定厂站的象限,然后厂站的具体坐标在对应象限范围内自动检索获取（检索范围包括象限边界线,即厂站中心坐标可位于象限边界线上）。

厂站在象限范围内坐标检索采用随机垂直或水平移动方式进行,以一个指定偏移量（默认设定为图元宽度的2 倍）将图元在范围内沿垂直或水平方向随机移动一步或多步,如果图元移动后新坐标未和已布局图元重叠且最小间距大于间距阈值（间距阈值默认设定为图元宽度的2 倍）则布局成功,否则重新进行位置检索直到该图元完成布局。布局过程中如果某个图元的垂直或水平方向已有其他图元,则本次位置检索优先选择在该垂直或水平方向进行,以此来保证布局范围内图元对齐。

2 基于神经网络的自动布线拓扑

2.1 路径规划神经网络

拓扑连线时,把潮流图画面分割成一个多行多列的密集网格,可以利用蒙特卡洛法［11］在网格上按步长逐个方向移动,以类似棋盘落子的方式逐步随机检索直到找到目标点完成线路连接,但是采用类似退火算法的方式随机移动检索无法确保步长方向选择的最优,因此需要设计一个步长的路径规划规则来确保每一步的步长方向选择接近理想结果。

首先,把潮流图画面逻辑划分成M×N的网格,其中,M为横向网格数,M=画布宽度/步长；N为纵向网格数,N=画布高度/步长。每个厂站在潮流图中用一个厂站图元标识（后续统称图元）,线路的路径查找是在一个网格中按照步长逐步检索直到完成图元之间的连线,每一个线路连线是由多个步长构成,步长可根据实际的画面规模设定,步长越短则需要越高的计算机算力,步长过长可能无法找到最佳线路,因此实际应用中可根据计算能力、图元大小等因素给出一个相对平衡的默认值。线路步长方向选择如图2 所示。

图2 线路步长方向选择Fig.2 Line step direction selection

为了保证生成线路接近理想结果,需要一个步长方向选择算法来决定线路下一步的最佳步长方向选择。不同的步长方向选择策略生成的线路是不同的,方向选择和最优线路之间存在关联关系。通过建立起输入和输出之间的关联关系,在每一步步长方向选择的时候用最优的关联关系规则来决定线路走向就可以找到最佳拓扑线路。

根据潮流图的拓扑特征可以抽象出影响线路步长方向选择的关联因子,比如步长方向选择时,希望距离目标图元的距离尽可能短,步长方向尽可能保持与之前步长方向一致（减少拐点）,同时步长方向前方区域图元应尽可能少（减少线路重叠概率）,步长选择应与已有相似线路的拓扑保持一致（已生成的拓扑连线会对后续生成的连线产生影响,因此线路进行步长方向选择时需参考与之拓扑关系相似的连线,方向选择时与其保持一致）等。因此,可以把距离因子、步长方向因子、步长方向图元密度因子、相似拓扑的步长因子等作为影响线路结果的输入因子。由于每个输入关联因子对结果的影响程度不同,为距离因子、步长方向因子、步长方向图元密度因子、相似拓扑的步长因子分别定义权重参数,可形成一个路径规划函数。每次步长方向选择时通过路径规划函数计算最优步长方向（各个步长方向中路径规划函数的评估值最大者为最优）,不断进行递归步长方向检索直到完成线路连接。同时,设定一个对最终生成线路进行质量评估的评判函数,并对已完成拓扑的线路根据线路质量评估函数计算其评估结果,可建立步长方向选择和线路质量之间的关联关系,从而形成了一个关联输入和输出的神经网络［12-14］。采用前馈神经网络模型构建的神经网络如图3 所示。

图3 输入输出关联关系Fig.3 Association relationship between input and output

图中：Rd为距离因子；Rs为步长方向因子；Rm为步长方向图元密度因子；Rss为相似拓扑步长因子；dw、iw、aw、sw分别为Rd、Rs、Rm、Rss的权重参数；Vs为某个步长方向的路径规划函数的评估值；VL为线路质量评估的评估值。

通过给路径规划函数设置不同的权重分别生成线路,并对每条线路进行质量评估,然后根据线路质量评估结果不断反向调整路径规划函数权重,实现了路径拓扑的自主学习。通过自主学习训练,把训练后的路径规划函数作为路径步长方向选择的规则,就可以根据图元的拓扑信息进行图元之间的拓扑线路连接。

2.2 线路拓扑训练

2.2.1 路径规划函数的定义

确定步长方向选择和线路质量之间存在的关联关系,需要对步长方向选择和线路质量进行规则定义,即定义路径规划函数和线路质量评估函数。

由于影响步长方向选择的因素包括距离因子、步长方向因子、步长方向的图元密度因子、相似拓扑的步长因子等,因此路径规划函数是由这些关联因素的函数叠加而成的。关联因子与最终结果不是线性关系,需要定义每个关联因子与输出之间的函数,即激活函数［15-16］。激活函数的选取［17］会影响学习的速率和质量,需要根据每个因子与线路拓扑的关联特性来设定对应的激活函数。

式中：Dm为区域图元密度,即步长所在方向特定矩形范围内图元个数（矩形范围高宽默认设置成图元高宽的5 倍,实际工程应用可根据成图效果调节）,区域密度Dm越接近0,函数结果越理想,即步长方向图元个数越少函数结果越优。

4）相似拓扑步长因子的激活函数

式中：Hss为判断当前线路是否存在相同拓扑关系的连线的布尔型变量；Ss为已拓扑连线当前步长的路径规划评估值。

如果当前步长所在线路存在相同拓扑,则Rss等于Ss；否则,Rss等于0,以此约束步长方向选择与已有相同拓扑保持一致。

对所有关联因子进行加权叠加,得出路径规划规则函数评估值为：

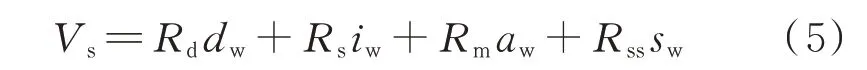
每个步长在选择“上”“下”“左”“右”时,根据路径规划函数计算出不同方向步长的Vs值,取Vs值最大者为最优方向选择。

2.2.2 路径规划函数的训练

路径规划函数中Ds、Do、Sd、Dm变量可通过坐标计算获得,Ss是已拓扑线路当前节点的路径函数评估值,需要对已拓扑线路步长评估值进行保存和标记,当前拓扑步长方向选择时可查找相同拓扑线路对应步长的评估值。

路径规划函数的权重参数dw、iw、aw、sw是未知的,需要通过深度学习来获得最优解。每次设置不同的权重值进行路径查找生成一条线路并进行线路质量评估就是一次训练,如果生成的线路的评估结果好于之前线路,则证明本次的权重值更接近理想结果,如此往复进行自主学习,如图4 所示。

训练的过程给路径规划函数的权重参数dw、iw、aw、sw从初始值开始,在取值范围内分配不同的值进行拓扑训练,学习的次数越多得到的线路结果也就越多,越容易接近函数的理论最优解。

关于线路的质量评估,需要根据实际的绘图规则设定一个线路的质量评判函数,比如按照拐点数量最少、线路交叉重叠较少、线路长度短等作为依据计算每个线路的评估值,评估值最高者为最优线路,线路的质量评估值VL计算如下：

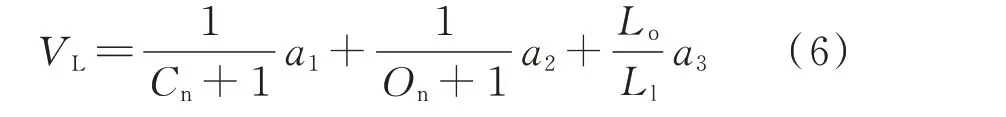
式中：Cn为线路的拐点数量；On为线路重叠交叉数；Ll为线路的折线线段总长度；Lo为线路起始点单拐点线段的总长度；a1、a2、a3分别为线路拐点、线路重叠交叉、线路长度的权重,取值范围为0～1。

由于不同电网区域拓扑复杂度不同,潮流图画面特征也存在差异,在实际应用中对绘图规则的要求存在差异,因此a1、a2、a3的取值可以根据实际的应用场景进行训练优化后设定。通过计算选择具有最高VL值的线路为最优连线,此最优连线对应的权重dw、iw、aw、sw就是路径规划函数的最优解。在线路拓扑连接时,根据这个最优解来进行线路路径检索,生成任意2 个厂站图元之间的线路连接。

3 基于拓扑训练模型生成潮流图

本文算法生成潮流图的流程见附录A 图A1。首先分区域、电压等级获取厂站模型数据和线路拓扑数据,然后根据厂站的拓扑关系,基于图元的拓扑深度和广度算法计算所有厂站的拓扑复杂度,并根据拓扑复杂度排序结果对所有厂站划分布局图层,然后从厂站模型数据中获取经纬度信息以确定每个厂站在布局图层的方位。最后,通过位置检索实现各个厂站在布局图层象限范围内的坐标定位。确定厂站布局后,需要依据路径规划函数的训练结果来完成线路拓扑。每条线路的拓扑从当前图元位置开始,检索过程按照递归方式路由查找路径,每一步步长方向选择时把训练好的路径规划函数作为路径方向选择的依据,分别计算出当前图元上、下、左、右各个步长方向的Vs值,取Vs最大方向节点为下一节点,逐步递归检索,直至找到拓扑连接的目标图元。在路径方向选择时,还需要过滤掉非法路径,比如路径遇到障碍、路径超出画面边界。如果遇到非法路径则进行排除,只针对合法步长方向进行路径规划计算。拓扑连线完成后,潮流图需要对厂站和线路名称文字进行标注和布局位置调整。为保证对齐和画面样式统一,文字的标注采用布局方位定位而不是坐标定位,标注文字按照厂站和线路的方位进行定位布局,厂站和线路的布局方位包括居中、上、下、左、右、左上、右上、左下、右下9 种。标注文字摆放时在对应图元的布局方位进行随机检索,如果布局方位与其他图元产生重叠则重新检索直到找到布局方位；如果布局检索失败则默认居中布局。线路是由n段垂直或水平的线段构成,所以线路的左、右方位分别对应首、末线段的起始方位,线路的上、下、居中方位则对应线路中位线段的上、下、居中方位。

4 算法验证

采用本文提出的算法中国以某省电网220 kV厂站拓扑数据进行自动拓扑生成潮流图,其中潮流图中共有厂站41 个,厂站间线路69 条。在路径规划函数训练时,由于不同步长对画面拓扑布线训练的结果有较大影响,为了防止结果偏差,根据画面规模分别设定10、30、100（单位：像素）3 种步长进行训练,利用3 个不同训练结果分别进行自动拓扑布线。

拓扑训练前需要设定线路质量评估函数的参数a1、a2、a3的经验值,参数的取值需要根据成图的要求和场景动态设定,本案例中依据潮流图特征,期望生成拓扑线路优先考虑减少交叉重叠,线路拐点和线路长度权重次之,通过对不同的质量评估函数输出结果进行比对,获得调优后的a1、a2、a3经验值分别为0.292、0.457、0.251。线路最大步长拓扑深度的设定（每条线路在潮流图画面网格中所有可能拓扑路径的步长之和）需要根据实际的计算机最大算力进行评估,应保证在计算机算力允许的情况下尽可能大地设置拓扑深度上限,否则训练不充分将导致结果落入局部最优。本次训练采用ThinkPad E14 计算机进行算法验证,经抗压性能测试,拓扑深度最大可达100 000,最终路径规划函数训练结果见附录B 表B1、表B2。

根据3 组训练结果的最优解,对220 kV 厂站分别自动布局和拓扑生成3 幅潮流图,效果如附录B图B1、图B2、图B3 所示。理论上训练量越大越容易接近期望的最佳值,但是由于步长过小,拓扑路径上限将以级数增加,受机器性能影响,实际运行时每条路径步长拓扑深度最多只能达到设定的上限阈值100 000,无法到达理论训练次数最大值,如图B1为步长为10 的成图结果,由于部分线路步长拓扑深度达到线路最大步长拓扑深度时仍未完成递归检索,反而使算法落入了局部最优的陷阱。步长为100 的训练结果由于拓扑路径选择过少导致训练不充分,同样存在局部最优的陷阱,而且从图B3 可见,由于部分图元间距小于设定的步长100,导致线路步长方向选择时找不到合法拓扑路径,造成部分图元未生成连接线。步长30 对应的训练结果则相对比较理想,基本达到了性能和效果的均衡,由图B2 可见,基于步长30 的训练结果进行布线生成的潮流图布线比较合理。实际算法应用时,可以根据画图规模、计算机性能等相关因素对步长等参数进行微调。

算法应用过程中也可以根据画面要求的差异动态调整拓扑策略,比如期望画面拓扑时减少线路环绕优先,此时可以对线路质量评估函数重新进行调整,减小重叠交叉权重a2,增加拐点权重a1,经过模拟测试设定线路质量评估函数参数经验值分别为0.489、0.218、0.293,重新进行训练后生成潮流图拓扑如附录B 图B4 所示。与图B2 结果相比,由于训练过程中路径规划函数选择步长方向时交叉重叠权重相对降低,路径拐点少,优先级更高,因此图B4 中部分线路的多拐点绕线被消除。实际应用时可根据画面的差异要求进行神经网络的调优和训练,从而灵活地获取期望结果。

5 结语

本文算法构建了一个基于线路路径拓扑的神经网络,基于此神经网络进行自主深度学习,通过训练后的线路步长方向选择策略实现厂站图元之间的线路连接来生成潮流图。与现有算法相比,本文算法可以根据不同差异化场景对神经网络输入输出参数进行调整和模拟训练来完成自动成图,可以弥补一些现有潮流图自动生成方法的局限性,为未来特定场景的潮流图自动生成相关实践提供参考。

理论上本算法中步长选取关联因子越多、步长越小,才能无限接近理论上的最佳结果,但实际应用时受限于算力因素,必须折中效果和计算负担。因此,如何优化路径规划函数使其快速准确地找到理论最佳值是未来研究的重点。

感谢国网华中电力调控分中心科研基金（HZ200623-62）对本文工作的支持！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。