后张预应力混凝土摇摆墙非线性分析
王嘉玮,周 威
(1.中国地震局地震工程与工程振动重点实验室(中国地震局工程力学研究所),哈尔滨 150080;2.结构工程灾变与控制教育部重点实验室(哈尔滨工业大学),哈尔滨 150090;3.土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨150090)
近年来的多次震害调查发现,强震下混凝土剪力墙结构体系可能发生严重损伤,面临震后修复成本高,且造成建筑物使用功能中断等突出问题[1-2]。而后张预应力混凝土摇摆墙作为一种可恢复功能结构,通过将墙-基界面处的约束放开,地震下摇摆墙墙体与基础间接缝张开,并由后张无黏结预应力筋和剪力墙的重力荷载提供恢复力,使摇摆墙往复摇摆,并在地震结束后恢复到初始位置,即实现墙体的自复位,其作为关键构件与框架结构组合成框架-摇摆墙结构可有效控制结构残余变形等损伤,再通过引入新型耗能元件辅助耗能,不需修复或仅需少量修复就能快速恢复建筑物使用功能。
结合试验、模拟和理论分析等方法,相关学者在基本原理、新型结构体系、抗震能力和性能分析等开展了较多工作,所提出的分析方法、设计理论和验证标准等,已纳入了相关标准[3-5]。Kurama等[6]提出了结构分析模型并采用试验与模拟相结合的方法,分析了摇摆墙的抗震性能,定性评价了剪力墙的自复位能力,试验表明其耗能能力差,极限侧移较大。Perez等[7]通过拟静力试验发现摇摆墙的有限损伤而非线性侧移显著,能保持自复位,在低周往复加载试验中表现出明显非线性-弹性行为。Nazari等[8-9]对4片5/18缩尺混凝土摇摆墙进行了振动台试验,模拟了多级地震动输入的摇摆墙动力响应,发现地震动下除了墙趾进入塑性阶段会耗散部分外部输入能量外,摇摆碰撞过程也会耗散少量能量。吴浩等[10]总结了在地震作用下摇摆墙受力性能,建立了摇摆墙截面纤维模型及数值模拟分析。目前,日本、新西兰等国家已将摇摆墙作为新型减震加固技术应用于实际建筑工程领域,如建于2010年位于新西兰惠灵顿维多利亚大学的Alan MacDiarmid大楼和皇家学会大楼均采用该类摇摆墙配合黏性阻尼元件作为主要抗震构件抵御大震造成的结构失效、破坏甚至倒塌。
常规以弯曲变形为主的结构非弹性变形主要集中一定长度的塑性铰区,开裂、屈服以及给定的塑性铰区长度下极限曲率和相应的转角均可结合试验和截面分析进行确定,具有明确的非线性分析的思路和方法。与此不同,对于后张预应力摇摆墙进行非线性地震响应分析,面临两个主要难题:一是,如何合理模拟以墙-基间开合转动为主要特征的墙片宏观变形以及由此引起的沿墙高通长的无黏结预应力筋的应力变化,尤其是进入较大的峰值侧移即非弹性大变形阶段,预应力筋应力如何发展,其与墙片侧向变形的耦合作用如何确定,以及在此过程中预应力筋对残余变形控制能力的变化等;二是不同侧移水平下墙-基控制截面的受压区高度为主要特征的局部行为的分析,即不同的峰值侧移下墙趾开合转动过程直接影响着截面压区高度,并间接反映着抵抗水平地震作用的抗弯能力,而且其抗弯能力也与无黏结预应力筋应力发展耦合联系。这是确定抗弯能力、极限变形能力、不同受力阶段加卸载刚度及其对残余变形影响等的前提和基础。
为此,以所完成的低周往复加载下后张预应力摇摆墙试件为分析对象,提出了以分布式轴向弹簧模型、共转桁架以及截面纤维单元相结合的分别模拟墙-基界面开合行为、预应力筋应力发展以及钢筋混凝土墙面的宏单元,并对试验结果进行了验证和拓展分析,为深化后张预应力摇摆墙地震非线性响应分析创造了条件。
1 摇摆墙往复加载试验简介
所完成的3片后张无黏结预应力摇摆墙试件,墙片与基础梁分开浇筑,接缝处采用高强纤维砂浆找平,通过无黏结后张预应力筋将墙片与基础连接,墙内普通钢筋在接缝处断开。为了方便加载装置安装,在墙体顶部设置了加载梁,并在加载梁两侧布置端板。摇摆墙示意见图1。
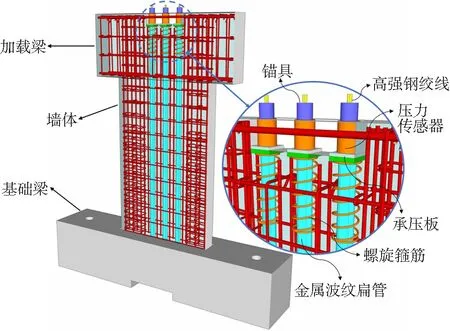
图1 摇摆墙示意
所有摇摆墙试件的配筋及几何尺寸相同,见图2,墙体高2 200 mm、宽1 000 mm(上部加载梁为1 500 mm)、厚140 mm(上部为200 mm),预应力筋布置在墙体对称轴及两侧150 mm的位置,同时为方便预应力筋张拉,在浇筑墙体与基础前,预先在上述位置分别埋置了金属波纹扁管。基础梁顶的摇摆墙拼装部位预留长1 040 mm、宽180 mm、深30 mm的凹槽,并采用高强度无收缩的纤维砂浆对其进行灌浆。为防止墙脚处混凝土发生严重损伤,在剪力墙边缘约束构件中距离基础以上1 080 mm的区域内对箍筋进行加密。各试件的其他主要设计参数见表1。

表1 试验墙体的主要参数

图2 摇摆墙试件配筋(mm)
试件的混凝土设计强度等级为C40,普通钢筋选用HPB300热轧光圆钢筋和HRB400热轧带肋钢筋,预应力筋为公称直径φs=15.2 mm的1 860级高强钢绞线。
低周往复加载试验在哈工大MTS 1 000 kN电液伺服作动器上进行,通过作动器对构件施加往复循环荷载以模拟地震作用下构件在往复振动中的受力特点。
试验前,将墙体与作动器通过铰接连接,作动器的加载中心与墙底距离为2 000 mm。试验加载装置示意见图3(a),通过控制加载点处的位移角来实现位移加载控制,位移角增幅为0.25%,每级加载循环2次,为防止预应力筋在加载过程中发生屈服,初始预应力较大摇摆墙SRW-1的位移角限值确定为2%,SRW-2、SRW-3加载峰值位移角为3%,加载制度见图3(b)。

图3 试验加载装置及加载制度
2 摇摆墙数值模型
目前,国内外学者针对后张预应力混凝土摇摆墙的数值模型研究[11]主要有:纤维单元模型(fiber elements model)、扭转弹簧模型(rotational spring model)、多弹簧模型(multi-springs model)以及实体单元模型(block elements model)等。其中,多弹簧模型由于建模方便、计算成本较低且能够准确地捕捉摇摆墙在横向荷载和地震动输入下墙-基界面的力学特性以及动力响应而在近年内受到广泛关注。因此,本文基于OpenSees地震工程模拟开放体系对低周往复加载试验中所用的3片预应力摇摆墙进行数值模拟分析,考察初始预应力水平和预应力筋面积这两个主要参数影响下摇摆墙的抗震性能。
2.1 主体墙片模拟
以往研究表明[12],在后张无黏结预应力筋及墙-基水平缝的联合作用下,摇摆墙由于地震作用发生摇摆,但是上部墙体始终保持在弹性状态下工作且不会发生剪切变形和破坏。因此,采用OpenSees单元库中内置的弹性梁柱单元(elastic beam-column element)模拟摇摆墙的墙片在循环往复加载试验过程中的压弯受力特性,忽略墙体的剪切变形。其主要建模参数见表2。

表2 弹性梁柱单元主要参数
2.2 墙-基界面水平接缝模拟
墙体与基础截面间水平接缝作为预应力摇摆墙的研究重点,需要进行精细化建模,以还原摇摆墙在摇摆过程中真实的墙趾开合过程以及接缝区域的力学特征。由于墙体与基础在墙趾接缝处不连续,在循环往复荷载作用下,墙体以靠近墙趾处某一点为圆心发生转动,同时另一侧墙趾抬起,其两侧水平接缝交替性开合。在此过程中,由于摇摆墙上部墙体内竖向钢筋与基础分离,不存在钢筋的黏结滑移作用,其对抗侧力贡献可以忽略,实际摇摆墙抗侧力系统由墙体内配置的无黏结预应力筋的拉力和受压侧混凝土非线性行为共同组成。
因此,如图4所示,在墙体与基础之间的间隙内采用多个接触弹簧进行连接,弹簧的底部采用固定支座进行约束,上部采用刚体相互并联,以保证摇摆墙截面符合平截面假定要求。
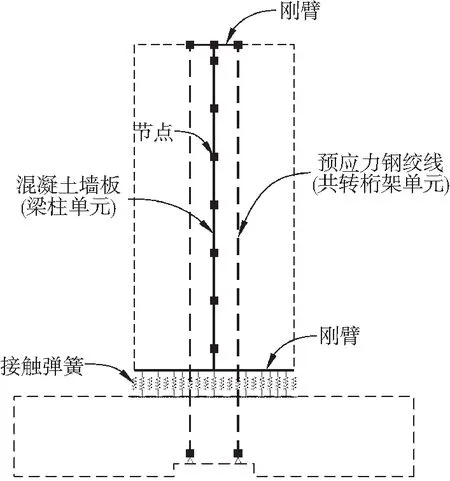
图4 多弹簧模型示意
在多弹簧模型建立过程中,弹簧的数量、有效高度、面积和材料本构作为其主要参数,直接影响到模拟的精度。根据Pennucci等[13]的建议,采用21个轴压弹簧进行接缝建模,这样不仅能够有效地预测墙体在摇摆过程中的中性轴偏移行为,同时能够获得良好的收敛效果和计算效率。接触弹簧的有效高度,可按照Perez等[14]建议,取预应力筋屈服时墙趾受压区高度的两倍或墙趾处边缘约束构件内竖向钢筋之间间距的两倍,在本文中,取后者即164 mm作为接触弹簧的有效高度。弹簧的面积由其所在的位置决定,在数值上等于墙厚与弹簧之间间距的乘积。
弹簧的本构模型选用OpenSees中的ConcreteCM材料来描述其单轴应力应变关系,见图5。该模型允许对单轴和滞回材料的建模参数进行校准,以模拟无约束和箍筋约束混凝土在反复受压或受拉作用下的滞回性能,并且能够还原混凝土材料一些重要的力学行为特征,如在反复受压和受拉条件下的连续滞后行为、增加应变值时与平滑卸载和重新加载曲线相关的刚度渐进退化以及裂缝的渐进闭合效应。
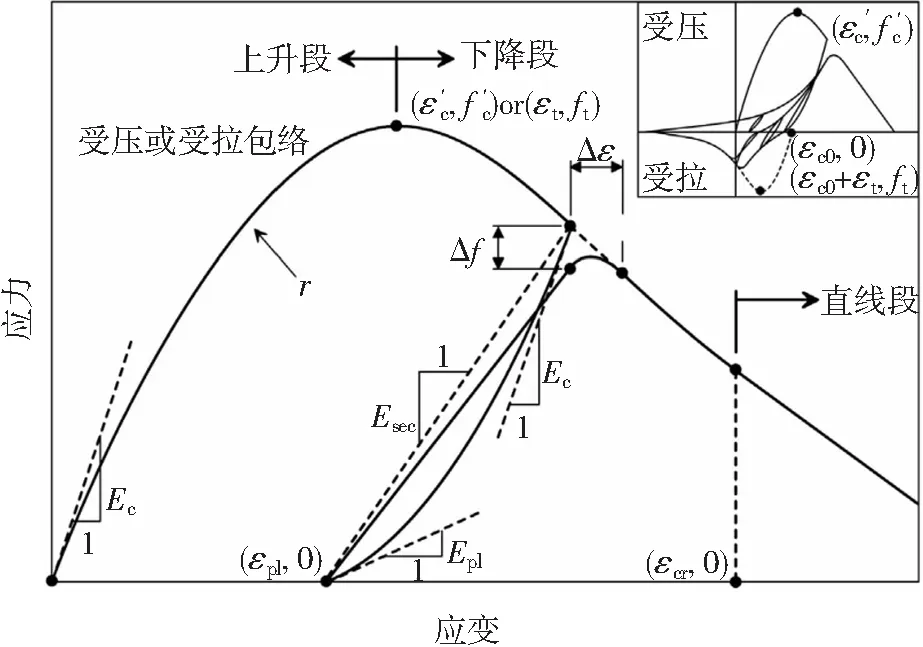
图5 ConcreteCM材料单轴应力应变关系
对非约束区混凝土,采用赵星[15]记录的混凝土材性试验数据,见表3。而对于箍筋约束区混凝土,采用Mander模型[16]来计算模型的应力应变关系,如图6所示,从而可确定ConcreteCM的具体建模参数。

表3 混凝土材料特性

图6 Mander本构模型
2.3 预应力筋模拟
采用corotTruss单元来模拟预应力筋的受力特性,见图7(a),该单元通过附着一个同向旋转的局部坐标系,允许桁架单元在全局水平上发生大的位移和旋转,因此考虑了非线性单元的几何形状,当摇摆墙墙体因摇摆而发生墙体抬升时,无黏结预应力筋的倾斜量与墙体底部转角是近似相等的[17]。如图7(b)所示,预应力筋材料选用基于Giuffre-Menegotto-Pinto本构关系[18]的Steel02模型,它可以同时考虑重复荷载作用下钢筋的等向强化。采用初始应力的方式施加预应力,Smith[19]的研究表明,摇摆墙内钢绞线锚固区域的混凝土和锚具变形会造成试验过程中的预应力筋刚度小于实测的刚度值,而这些局部变形无法在材性试验中准确地测出,因此在对Steel02模型参数中的弹性模量定义时,取0.75倍的材性试验实测值,将钢绞线线弹性范围内的初始刚度予以折减。其他钢绞线参数参考文献[15]中的实测值进行取值,见表4。

表4 钢绞线材料特性
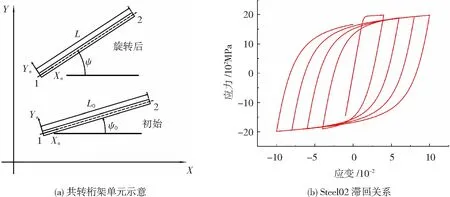
图7 预应力筋单元及材料本构
在处理预应力筋的锚固点时,不是仅仅采取简单的铰接,而是采用二节点组合弹簧单元twoNodeLink单元模拟,在预应力筋受力的自由度方向采用单轴受压材料本构(uniaxialMaterial ENT)将锚固端主从节点连接,同时并联一个刚度非常小的弹性材料(uniaxialMaterial Elastic)以避免钢筋反向受拉时刚度完全丢失。
3 非线性响应分析
3.1 荷载-位移滞回曲线
试件SRW-1~SRW-3的试验荷载-位移滞回曲线与模拟计算结果对比见图8。从图8可看出,摇摆墙SRW-3较SRW-1、SRW-2配置的预应力筋数目最少,因此其水平承载力较低,抗侧刚度较小。3片摇摆墙的滞回曲线均表现出明显的捏拢现象,说明该类剪力墙的耗能能力较差。在每级位移加载完成后,摇摆墙在卸载时位移未回归至零点,这可能是由于墙体与基础在低周往复加载过程中不可避免地存在少量的滑移。从摇摆墙滞回曲线的模拟结果中可得到与试验结果相同的结论,3片摇摆墙模型最大峰值侧移条件下的水平承载力计算值分别为137.7、138.7、106.3 kN,与试验值之比分别为1.042、0.996、1.061,峰值荷载下极限变形计算值与试验值之比分别为0.993、0.998、0.995,平均值为0.995,方差0.005。模型的滞回曲线与试验结果总体吻合较好,峰值承载力与极限变形的差距均在10%以内。但模拟的滞回环包络面积均小于试验值,说明模拟低估了剪力墙中混凝土损伤造成的能量损失,同时,在加载过程中作动器的系统摩擦力以及基础梁的接缝处灌入的高强纤维砂浆与墙体间黏结摩擦力也会耗散一部分能量。
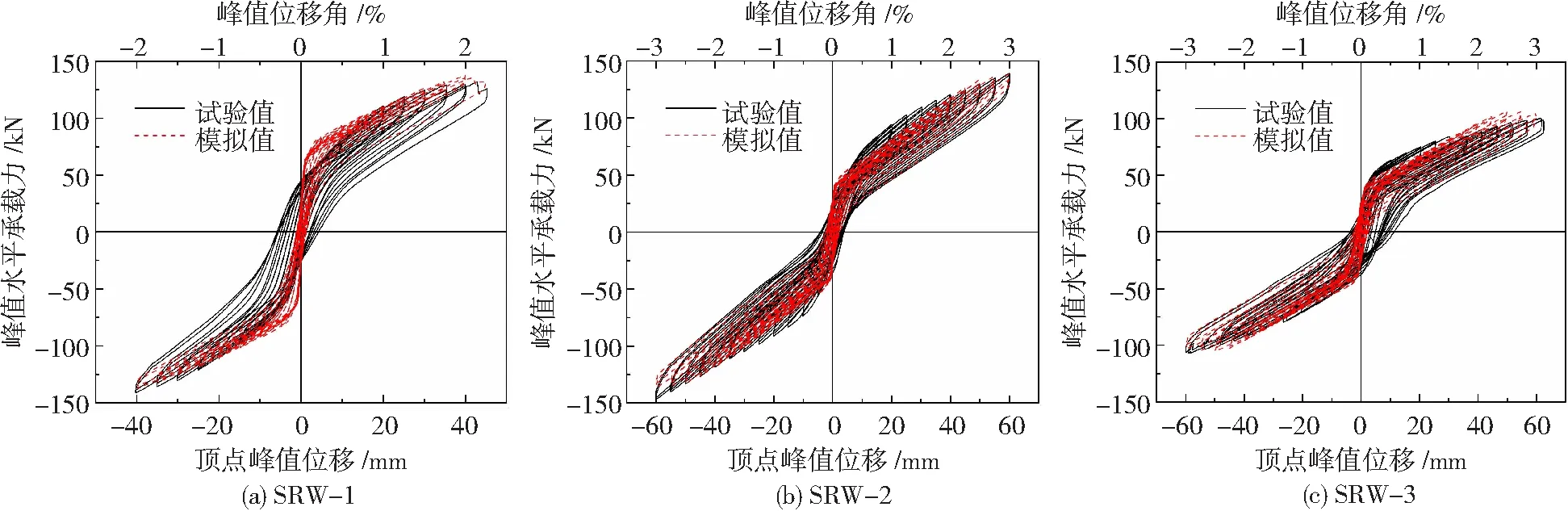
图8 试验滞回曲线与往复加载模拟对比
3个模型在峰值侧移下的绝对残余变形仅为1.17、2.28、2.49 mm,残余侧移比分别为0.060%、0.121%、0.124%。对比3个试件的模拟结果都不能很好的反映真实的残余位移,均小于试验结果,一部分原因是在最后几个循环加载周期内,试件墙角的保护层混凝土被压碎,增大了剪力墙的残余变形,而在数值分析中难以实现这一状态下的模拟;另一部分原因是在试验加载过程中,墙体与基础之间存在滑移,造成试验滞回曲线的不对称和残余变形的增加,但在模拟中由于采用对称加载,并不会考虑这一点。
3.2 骨架曲线
通过将滞回曲线中每一级循环加载达到的水平荷载的最大峰值相连,得到模型墙体的骨架曲线,采用同样的手段,对试验结果进行处理并与模拟结果进行对比,见图9。
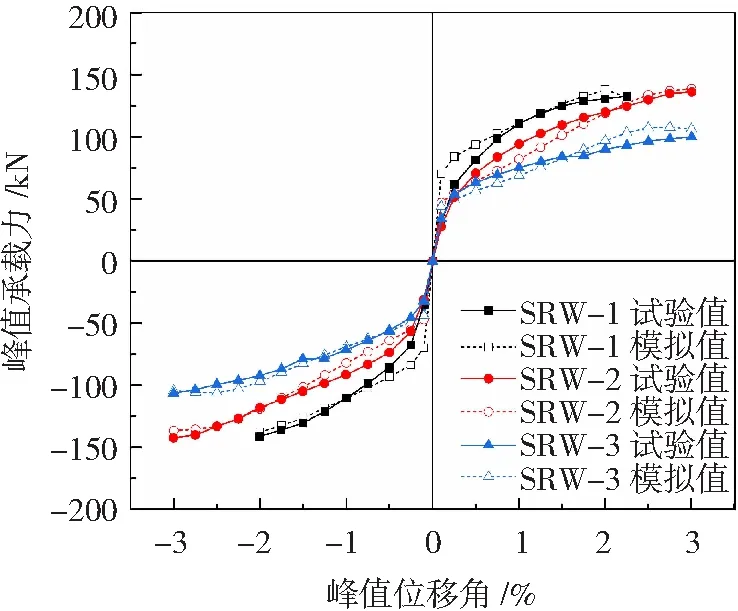
图9 试验骨架曲线与往复加载模拟对比
3片预应力摇摆墙骨架曲线的模拟结果和试验结果总体趋势是一致的,当构件加载到一定位移(对应位移角约为0.25%)时,其刚度会发生明显的降低,反映在骨架曲线上便是有一个转折点,在这个点之后,随着位移增大,水平承载力提高的速度有所放缓,根据Kurama等[20-21]研究得到的结论,该点是由于墙-基接缝的张开程度逐渐增大以及混凝土材料的非线性程度加深从而使得墙体刚度发生显著降低。但是,模型的计算结果过高地估计了构件的初始抗侧刚度,因此在加载初期,相同位移加载条件下,水平承载力计算值均大于试验结果,这可能是因为在模拟分析时未能较好地考虑墙体与其下部基础梁之间接缝处纤维砂浆垫层对本次拟静力试验结果产生的影响。
3.3 耗能能力
为了进一步分析模拟结果,对比了模拟和试验构件的耗能能力。本文选用各级位移加载下的单圈耗能和累积耗能作为衡量摇摆墙耗能能力的主要依据,见图10。

图10 耗散能量与往复加载模拟对比
从图10看出,3片摇摆墙的单圈耗能计算值与试验值在趋势上是一致的,结合试验现象可发现,随着位移角的增大,摇摆墙墙趾部位受挤压发生塑性变形,构件的耗能能力随之增强,但是由于上部墙体大部分区域仍处于弹性阶段,并未发生弯剪破坏,因此耗散能量较少,在实际工程中应通过在墙趾处附加阻尼器(如摩擦耗能元件、速度黏滞型耗能元件)或者在墙趾处配置耗能钢筋的方法在保证其结构变形能力和恢复能力的同时提高其耗能能力。与试验结果相比,有限元模型所得到的单圈滞回曲线包络面积计算值均偏小,原因如上文所述。
随着构件侧移增大,试验中的3片摇摆墙的累积耗能增长速度逐渐增加,但是当增大到一定斜率后继续加载,增长速度趋于平稳,累积耗能近似呈线性增长,这与模拟结果存在差异,这是由于此时摇摆墙墙趾处的部分区域混凝土被压碎退出工作而使得构件的耗能能力有所削弱,而在模型中则无法实现该损伤累积的模拟。
3.4 受压区高度变化
摇摆墙抵抗横向水平荷载的性能主要是由墙体与基础界面水平接缝的力学特性决定的,接缝的张开程度对结构的刚度特性影响重大[10]。此外,接缝之间的摩擦力是摇摆墙抗剪承载力的主要来源,因此能否准确的模拟墙体在摇摆过程中的抬升情况及中性轴深度的变化是验证数值模型是否合理的重要因素。
在地震作用下,摇摆墙墙趾处墙体与基础梁界面处的水平缝会发生开合。通过在摇摆墙底部预先竖向布置的位移计可以测出墙体在每级峰值侧移时摇摆墙墙趾的抬升量,采用线性回归分析的方法找到最佳拟合曲线,通过该拟合曲线与横坐标轴的交点,能够得到墙体的受压区高度。如图11给出了受压区高度随每级峰值位移的变化关系,通过将模拟结果与试验结果对比可看出,计算结果能够从总体上把握接缝张开程度随结构变形的变化规律,墙趾抬升的上下限值与试验结果基本吻合。
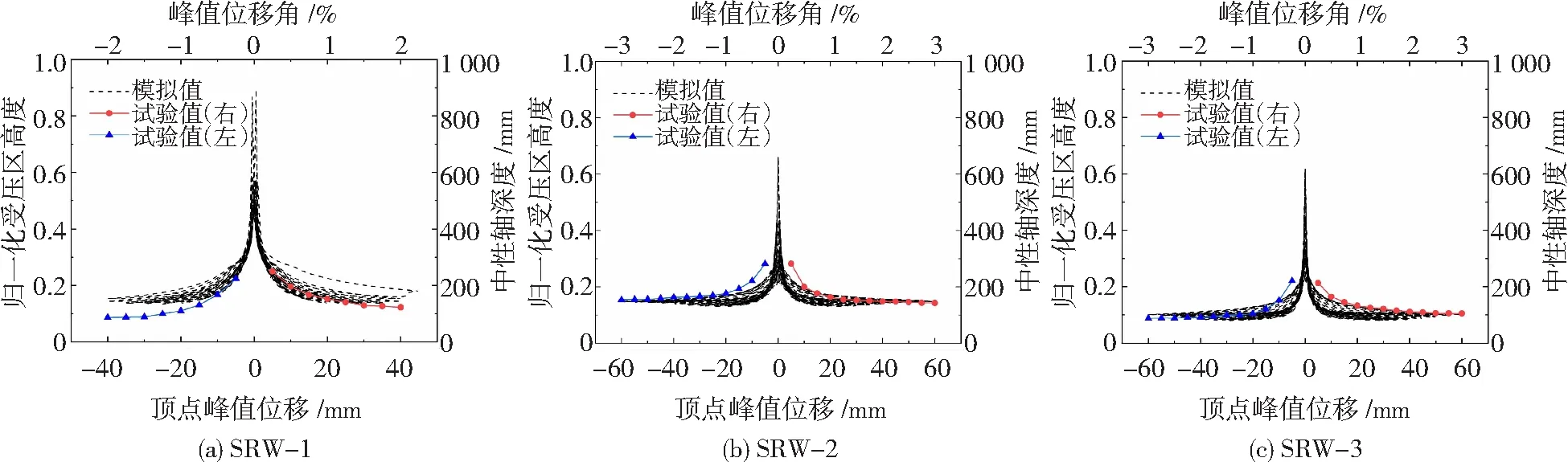
图11 受压区高度变化与往复加载模拟对比
3.5 预应力变化
预应力筋作为本次试验与模拟分析的重点,直接影响到自复位摇摆墙的抗侧刚度以及承载力。因此在试验过程中采用穿心式力传感器进行实时监测,并在图12给出了往复循环加载试验下自复位摇摆墙中预应力筋应力随位移角的变化情况,与模拟结果进行了对比。

图12 试验预应力筋应力变化与往复加载模拟对比
由图12可看出,从试验开始到最后一级循环加载结束,预应力钢绞线的应力未超过其屈服应力,说明墙体内的预应力筋始终都保持在弹性状态下,对3片自复位摇摆墙的有限元模型中也可以得到相同的结论。通过在建模过程中对预应力筋初始刚度的调整,模型的预应力筋应力变化斜率与试验结果吻合较好,在加载过程中的预应力变化趋势基本一致,证明采用多弹簧模型能够提供合理的预应力变化预测。但是,由于模型是在较为理想的条件下建立的,未能考虑在加载过程中墙体的侧向滑移,因此,相比两侧预应力筋,位于摇摆墙中轴线上的预应力筋应力损失在模拟结果中未能得到很好的体现。
4 结 论
考虑预应力筋的初始预应力水平和预应力筋面积对摇摆墙进行了拟静力试验的非线性分析,基于OpenSees分析程序建立了预应力摇摆墙多弹簧模型,详细介绍了建模方法,并与往复循环加载试验结果进行对比,对摇摆墙滞回曲线、骨架曲线、刚度退化、耗能能力、残余变形、受压区高度变化以及预应力变化等多个指标进行了评价,主要结论如下:
1)多弹簧模型能够较为准确地把握摇摆墙的滞回特性,模型的峰值水平承载力与试验结果相差在10%以内,同时对极限变形提供了准确的数值预测。
2)模型能够较好地反映该类剪力墙在拟静力加载条件下的刚度退化、受压区高度变化以及预应力筋斜率变化趋势。模拟与试验结果整体吻合较好,验证了多弹簧模型的可靠性和合理性。
3)模拟和试验结果均表明,与普通钢筋混凝土剪力墙相比,摇摆墙的整体刚度小、卸载后残余变形小、自复位效果好,但是滞回曲线较狭窄,耗散能量较少,耗能能力较差。在实际工程中应在保证其自复位能力及承载能力的同时,可采用附加耗能元件或在墙趾处配置内部锚固的耗能钢筋的方法提高其耗能能力。

