稠密化重建稀疏性特征多图像3D构建实现
张海军,钟向阳,陈映辉
(1.广东省山区特色农业资源保护与精准利用重点实验室 广东 梅州 514015;2.嘉应学院 计算机学院,广东 梅州 514015;3.嘉应学院 数学学院,广东 梅州 514015)
0 引 言
三维重建是利用计算机技术建立客观世界的虚拟化模型的一种方法,其应用广泛,包括手术医疗、航天科技、娱乐游戏等方面.进行3D重建通常面临一些相关的问题:①需要较深的理论基础实现2D与3D的互映射;②需要基于大量的数据进行特征点的提取及降维等操作,所以运算量较大.因而使用常规方法难以实现有效的3D重建,需要探索新的有效的方法.如使用连续平面图即2D图序列,提取主特征信息,还有基于稀疏点进行3D构建,基于特征点分层的构建[1-2],之后又有了基于稠密特征的称为点云的3D构建,如区域扩展立体特征对稠密匹配法[3].然而传统的方法主要有如下不足:首先,对目标图像的质量要求高,因而对拍摄设备要求也高;其次,因目标图像质量高,所以运算量大,运算时间长,对计算能力的要求也非常高,常规设备难以达到或运算速度过慢;再次,对于普通目标对象容易受环境因素的影响,如光照、明暗、强度,是否遮挡和不同视角拍摄等;另外,因为条件的限制,难以用较高端的拍摄工具,用常规的相机或移动手机相机拍摄.为此,本文探讨并实现:(1)可基于不同类型不同质量的图形的重建,即适用于不同的场景;(2)对光照、亮度、图像明暗度和清晰度等具有较强的鲁棒性的重建;(3)可以基于较少的图片完成重建,计算量较少,运算效率高;(4)因而本文方法适用范围大,除了质量高的图片,也非常适合普通设备如用手机移动终端相机拍摄的场景的重建.
为此研究稠密化重建稀疏性特征多图像3D构建实现,主要原理流程为:首先,利用拍摄的多样本图像进行检测与提取,获取2D特征点;其次,利用相机的自标定,创建特定的矩阵Ρn投影;再次,结合获取的2D图像特征点,通过标定Ρn矩阵进行逆投影从而生成稀疏3D特征空间点;最后,通过一致性邻域扩展生成稠密点集,借助滤波操作完成精确3D目标模型构建,研究流程的实现如图1所示.

图1 稠密化重建稀疏性特征多图像3D构建实现流程图
1 提取多图像2D特征点
利用限制几何约束,采集样本图像集n幅,表示为{I1,I2,…,In},基于每幅图像利用Harris角点检测和SIFT特征检测实现特征点的有效提取.
2 标定投影矩阵Pn及评估3D坐标
为了精确地重建3D目标点,首先匹配多幅图像对应的特征点对,然后通过三角测量把3D特征点变换为3D点,并用几何约束求精度,先建立3D点到2D点的映射方程为:
λijxij=PiXj
(1)
(2)
式中:K为内参矩阵,∝为非零伸缩因子条件下相等,Ω*为绝对曲面映射图,估计内参求出Ki,估计PE反向投影即逆映射2D点集实现3D场景X重建.
2.1 重建多图像射影
利用式(1),设W3m×n为测量矩阵,并使W=λijxij,展开得:
(3)
即W可表示为运动矩阵P3m×4与空间目标模型X4×n矩阵的积,设λ1j=1,对各图像估计求得基本矩阵F1j和极值点e1j, 从而得:
(4)
再对W进行SVD.
2.2 欧氏重建实现自标定
通过式(3),用绝对二次曲面Ω*约束实现线性变换HX运算,对运动矩阵P作逆变换PH-1[5-7]运算,得到:
W=PX=PH-1HX=PEXE
(5)
式中:H为4×4的非奇异单应矩阵,PE为投影矩阵,XE为目标模型.对于自标定算法,设内参矩阵K为:
(6)
式中:fx和fy为焦距,s为倾斜因子,u0和v0为主点坐标,定义具有射影空间不变性的模型为[8-9]:
朱虹则在《走进全域旅游新时代》一文中提出,全域旅游发展的特性在于:管理的统筹性、产业的优势性、发展的融合性、供给的丰富性、服务的便利性和目标的共享性。
(7)

(8)
设参考面的投影矩阵为P1=[1|0],得:
(9)

(10)
以:
(11)

(12)
3 稠密化稀疏特征点3D构建
基于式(11)得3D模型,再用面片重建[10-12]稠密点云.
3.1 形成小片面——面片
对3D曲面的小区域矩形化逼近得面片如p,包括中心坐标c(p),法向量n(p),光心O(Ii),有可视p投影的2D参照图像R(p),通过如下运算[13-15]生成种子面片集:

(13)
2)使法方向和p到O(Ii)的方向间的夹角小于预设值t,统计出可见图集V(p):
(14)
3)把最优图像作为参考图:
(15)
式中:h(p,I,J)为光度差异度.
4)计算图像灰度互相关,把具有相似性约束的图赋给V*(p):
V*(p)={I|I∈V(p),h(p,I,R(p))≤α}
(16)
5)作深度数量约束|V*(p)|≥γ,得种子面片p为:
(17)
3.2 面片的约束迭代扩展
基于相关约束实现邻近区域扩展成稠密面片集[16-19]:
C(p)={Ci(x′,y′)|p∈Qi(x,y),|x-x′|+|y-y′|=1}
(18)
再优化,即删除基于如下条件的面片p′:
|c(p)-c(p′)·n(p)|+|c(p)-c(p′)·n(p′)|<2ρ1
(19)

n(p′)←n(p),R(p′)←R(p),V(p′)←V*(p)
(20)
光线交点即中心c(p′),在V(p′)集由灰度一致性值得V*(p′),进一步优化并增加光束化直线式限制,更新V*(p′),直到生成结果集.
扩展完邻域后,对扩展后的面片集进行滤波,首先,基于可见一致性约束,即基于式
(21)
去掉不正常面片,g*(p)为光度相异均值,然后基于下式
|V*(p)|<γ
(22)
也可确定可删除的异常面片.最后,去掉与其8个邻域内的面片数的比小于0.25的面片块.
4 实验与分析
4.1 实验环境
Windows 7, Visual Studio 2015, OpenCV 3.0; Intel(R)Core(TM)i7-2630QMCPU@2.0GHz, RAM8GB, NVIDIA Quadro 4000.
4.2 结果与分析
传统的重建方法主要有基于树邻居的重建和基于图邻居的重建,但它们要求图像数量多、质量高,因而运算量大,用时较长,而本文方法可以利用少量以及普通质量的图像,计算量更小,用时更短,特别适合利用普通相机拍摄的常规和少量的图像,重建出质量较高的模型,具体过程为:①对多个不同的目标分别从侧面、正面及环绕等角度,以定长和变长距离等方式分别拍摄到20、30和50幅图像;②基于目标,利用Harris及SIFT提取特征;③自标定微型摄像机参数并求出Pn;④计算相关量:焦距,表示为f,旋转矩阵,表示为R,3×3维r1…r9,平移矩阵,表示为Τ,3×1维t1…t3,可得详细数据;⑤利用得到的相关量对2D特征点逆映射成3D点,进一步得到稀疏的面片种子;⑥再基于相关约束条件实现邻近区域扩展生成稠密面片集,滤波成精确的3D模型;最后,重建的目标与真实三维物体较接近,可视性较高,相关过程和结果如图2所示.
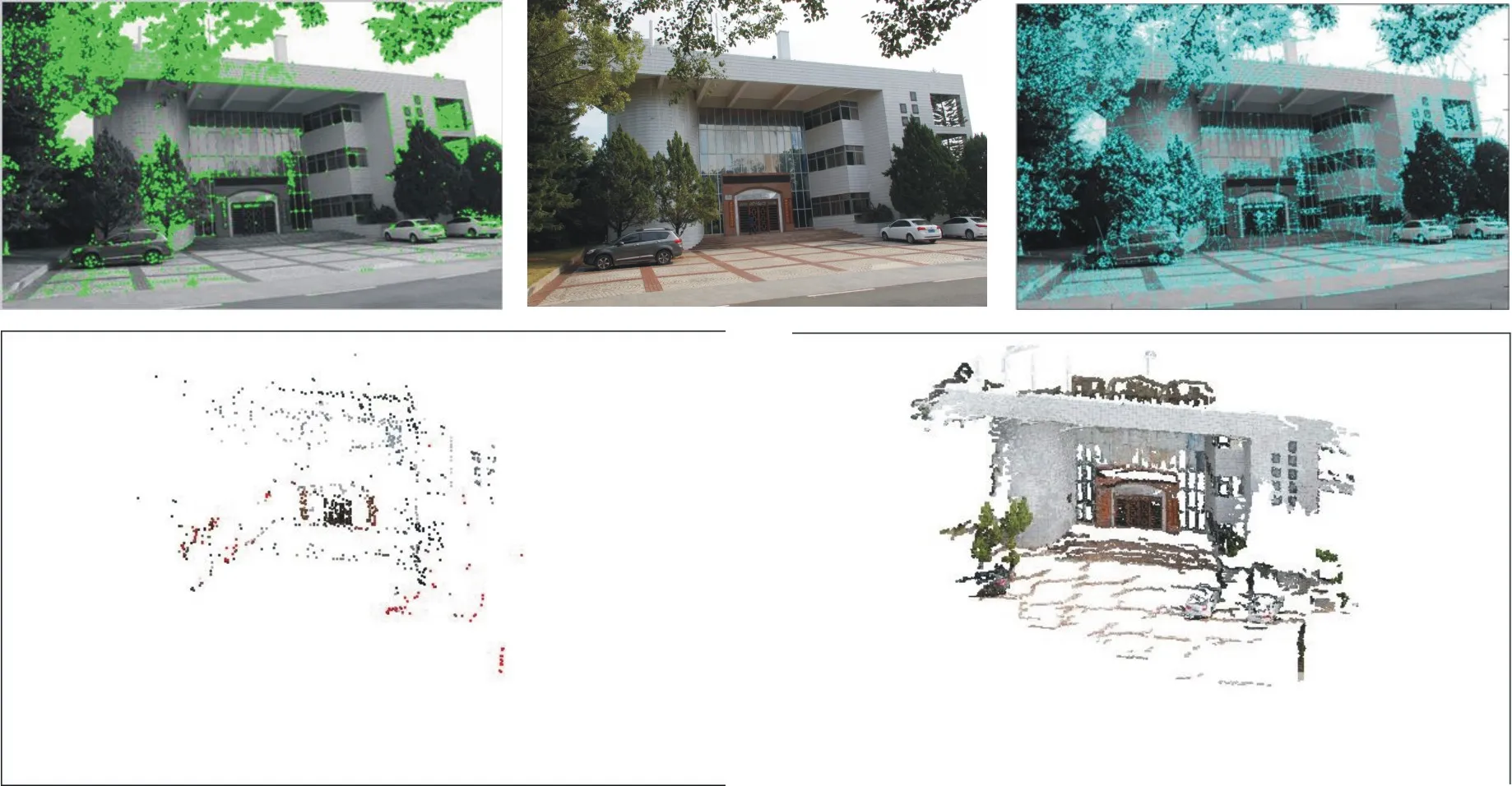
图2 相关过程及结果图
另外,通过实验得出对通过不变焦距方式采集的目标进行重建的3D模型比对通过变焦距方式采集的目标的重建模型效果更好,而且不同的光照强度和遮挡对重建的模型也有较大的影响.不变焦距采样目标的样图如图3所示,重建的模型集如图4所示;变焦距采样目标的样图及重建的模型集如图5所示.

图3 不变焦距采样目标的样图

图4 重建后的3D模型集

图5 变焦距采样目标的样图及重建后的3D模型集
5 结 论
本文实现了真实3D模型的重建,通过自标定微型摄像机参数建立投影矩阵,对2D点逆映射成3D点,通过扩展和滤波,由稀疏至稠密,生成精确3D目标模型.同传统方法相比,本文方法具有如下优势:(1)可基于不同类型不同质量的图形的重建,即适用于不同的场景,如本文利用普通移动手机相机拍摄的图片也获得了质量较高的重建模型;(2)对光照、亮度、图像明暗度和清晰度等具有较强的鲁棒性;(3)可以基于较少的图片完成重建,计算量较少,运算效率高;(4)传统的重建方法主要有基于树邻居的重建和基于图邻居的重建,它们对图像的质量要求较高,运算量大,用时较长,而本文方法适用范围大,除了质量高的图片,也非常适合普通设备如用手机移动终端相机拍摄的场景的重建;(5)实验结果表明构建的3D模型接近真实,同时通过实验发现:采集图像时要多角度、无遮档,定长焦距比变长焦距效果好等.总之,三维重建难度大、复杂性高以及计算量大,今后将进一步探索和研究,如基于集群以提高并行度、基于再稠密化以获得更大精度等.

