某疫苗储运箱结构设计及瞬态热流分析

汤云峰，李长玉，肖 颖，李细霞，戚 松

（广州城市理工学院 汽车与交通工程学院，广州 510800）

0 引言

疫苗是预防人类和动物传染病扩散最重要的手段之一。疫苗预防传染病的效果除了受其本身研发制造水平影响之外，储运条件也至关重要，一般要求冷冻疫苗在运输过程中温度要低于-15 ℃，灭活疫苗在运输过程中温度要在2～8 ℃之间［1］。保温箱经常被用来运输疫苗。为了提高保温箱的保温效果和降低研发成本，众多研究人员针对保温箱运输过程中温度场变化，进行仿真分析和试验研究，具体可归结如下：

刘翠娜等［2］设计了一种可以用于药品及疫苗存储运输的便携式储运箱，并且通过Ansys软件对该储运箱的冷藏保温效果进行了分析比较。廖阳明［3］利用半导体制冷原理，设计了一种便携式的恒温箱，利用精准的控制策略，可精确控制储运过程中箱内货物的温度。李细霞等［4］设计了一种冷板可拆式保温箱，构建了保温箱的三维模型，通过有限元的方法计算该保温箱的保冷效果。朱宏等［5］利用试验的方法研究了不同的外界温度对保温箱保温效果的影响。潘欣艺等［6］利用Fluent软件建立了某保温箱的三维模型，分析了保温隔热材料对保温效果的影响。纪秋平等［7］设计一种可折叠的冷链保温箱，并且分析了折叠保温箱和整体保温箱在储运效果方面的差异。王建军等［8］设计一种蓄冷式多温区保温箱，建立了该保温箱的瞬态传热模型，计算得到了各温区的有效保温时间。豆孟柯等［9］从疫苗运输箱箱体保温材料的选择、箱体热阻计算、蓄冷剂材料选择、蓄冷板放置方式、温度监控技术等几个方面分析阐述了疫苗运输箱设计制造过程中要注意的问题。LI等［10］利用计算流体力学的方法研究了某绝热箱箱体的温度场分布情况，研究了外部空气流速对箱体温度场分布的影响。KUCHARK等［11］建立了一种数学模型来计算保温箱的瞬态传热情况，研究了材料导热系数等参数对温度场分布的影响。罗大伟等［12］建立了保温箱和蓄冷剂的三维耦合模型，利用有限元仿真技术对保温箱内部流场进行分析。方文康等［13］基于Fluent软件对多温区包装箱温度场进行了仿真分析，并对分析结果进行了试验。李兵等［14］利用试验的方法研究了不同冰袋数量对保温箱保温效果的影响。

因自带电源及制冷设备的恒温箱成本高，体积大，质量重，利用率较低且故障率较高，越来越多的工程技术人员采用共晶板蓄冷的方式储运疫苗。本文设计一种采用共晶板供冷的便携式恒温箱，用于灭活疫苗的存储和运输。利用三维建模软件建立储运箱的模型，结合几何模型，简化后建立储运箱瞬态传热的数理模型，通过有限元方法计算在恒定气温和时变气温边界条件下箱内疫苗包裹温度场的变化情况。分析共晶板厚度对有效保冷时长的影响，得到有效保冷时长和共晶板厚度之间的关系曲线。

1 疫苗储运箱的结构设计及三维建模

1.1 疫苗储运箱的结构设计

疫苗在运输过程中一般先从冷藏设备中取出打包再装入储运箱，本文设计的疫苗储运箱按需求应可装载240×240×200 mm的疫苗包裹。设计储运箱外壳底部尺寸为400×400 mm，厚度为2 mm，高度为240 mm。为了保证保温效果，箱体采用厚度为40 mm的泡沫进行隔热。箱体内部壳体厚度为2 mm。箱盖分为上壳体和下壳体，壳体厚度均为2 mm。箱体底部内侧设置卡槽，四周可分别放置不同厚度的共晶板。共晶板内灌注蓄冷剂。具体的结构如图1所示。

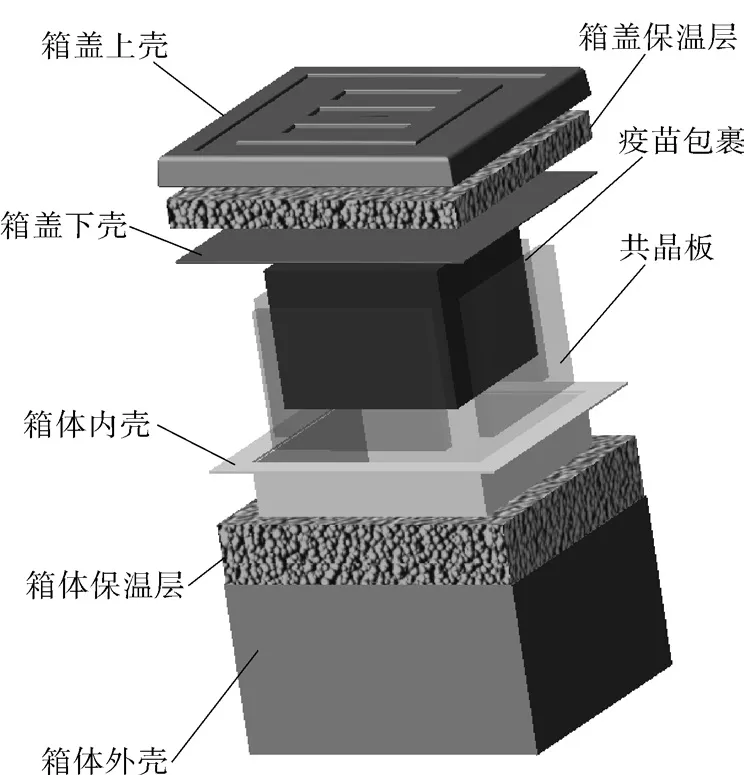
图1 疫苗储运箱的结构图Fig.1 Structure diagram of vaccine storage and transportation box

1.2 疫苗储运箱各部件材料及工艺要求

考虑疫苗储运箱可多次重复使用，箱体外壳需采用可抗冲击、抗磨损、化学性能稳定的材料制作。经查阅相关文献后选取聚乙烯材料［15］。储运箱的保温层是保证储运效果的关键部件，需要选取热传导系数较低的材料，同时为减轻箱体自重，提高运输效率，保温层需选用密度较低的材料。查阅文献知，当保温效果要求不高时，可采用价格较便宜的聚氨酯材料；对保温效果要求较高时，可采用真空隔热材料［16］。为达到较好的运输效果，需要在共晶板内装入蓄冷剂。蓄冷剂的相变温度直接影响到疫苗运输的效果。相变温度较高的蓄冷剂容易造成在运输过程中温度超过要求的最大值；相变温度较低的蓄冷剂容易造成运输过程中温度低于要求的最小值。疫苗储运箱一般可选用相变低于0 ℃的共晶盐，相变温度为0 ℃的水，或者相变温度为5 ℃的RT5HC作为蓄冷剂。南方地区夏季温度较高，为保证足够长的有效运输时间，本文选取相变温度为-5 ℃的共晶盐。

2 数理模型的建立

2.1 模型的简化假设

为了计算疫苗储运箱运输过程中传热情况需要建立数理模型，在建立模型之前做如下简化处理：（1）因箱体和箱盖外壳厚度相对于保温层厚度很小，同时其热传导系数较大，计算时忽略其影响；（2）疫苗提前打包好放入储运箱内，为便于计算将疫苗包裹视为规则立方体；（3）假设疫苗储运箱密封良好，不考虑漏气的影响；（4）箱体共晶板以及内装物之间的缝隙，假设为薄空气层。

2.2 控制方程

以储运箱底部一角为原点，建立相应的坐标系，如图2所示。相应的控制方程［17］：

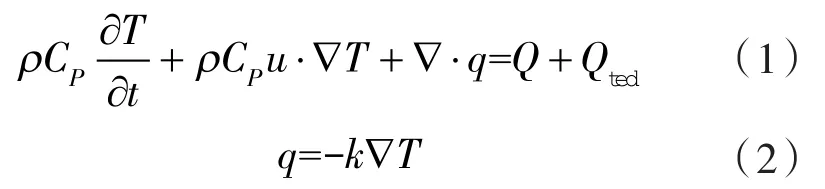
式中 ρ——疫苗储运箱各部件的密度；

CP——疫苗储运箱各部件的恒压比热容；

u——部件相对运动速度；

k——疫苗储运箱各位置的热传导系数；

Q——内部的热源；

Qted——热弹性阻尼；

∇——微分算子；

q ——热流量；

T——温度。

图2 数理模型的坐标设置Fig.2 Coordinate setting of mathematical model

2.3 边界条件

假设疫苗储运箱的各表面均暴露在空气中，与空气对流换热，相应的边界条件为：

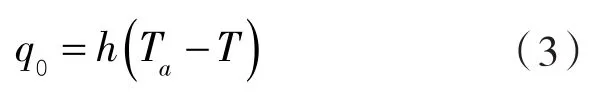
式中 q0——疫苗运输箱表面对流换热热流量；

h—— 空气与疫苗运输箱表面的对流换热系数；

Ta——外界环境温度。

2.4 初始条件

相应的条件设置：共晶板的初始温度为Tcool，箱体及箱体内空气的初始温度和计算开始时环境温度Ta相等，疫苗包的初始温度为Tina。

3 疫苗储运箱的瞬态热流分析

3.1 模型验证

为了验证仿真模型的正确性，将建立的模型和文献［6］研究的保温箱，设置同样的边界条件和初始条件，并进行分析和计算，对比分析计算结果和文献［6］结果之间的误差。误差最小为-0.2 ℃。误差最大为1.5 ℃。一致程度较高，从而可验证方法的正确性。

3.2 条件设置

在计算疫苗储运箱保冷效果时，需要箱体各部件材料的热物理参数，如表1所示［18］。

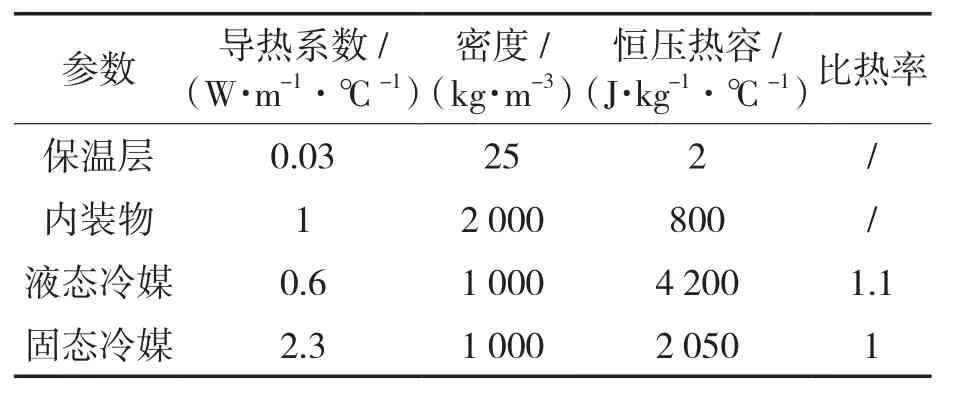
表1 储运箱各部件热物理参数Tab.1 Thermophysical parameters of storage and transportation box components

其中空气的热物理参数取默认值。根据国际安全运输协会（International Safe Transit Association，ISTA）标准，在运输过程中需要考虑4种情况：第1种为冰冻或冬天，最低温度设定为-29 ℃；第2种为热带气候，最高温度设定为38 ℃；第3种为用户基于已知条件设置自定义温度，本文设定为20 ℃；第4种为用户基于已知条件设置循环变化温度，本文设定为24小时内随时间在18～28 ℃之间波动。

图3表示共晶板厚度为25 mm时，不同环境温度下不同时刻疫苗包裹中截面温度分布情况。当环境温度取极限最低温度Ta=-29 ℃，t=6 h时疫苗包裹的温度已经低于2 ℃，此时保温箱有效保温时间在4～6 h。当环境温度取值Ta=20 ℃，t=80 h时疫苗包裹温度高于8 ℃，有效保温时间在78～80 h。当环境温度取最高温度Ta=38 ℃，t=30 h 时疫苗包裹温度高于8 ℃，包裹的有效保温时间在28～30 h。当环境温度取值随时间18～28 ℃波动变化，t=70 h时疫苗包裹温度高于8 ℃，疫苗包裹的有效保温时间在68～70 h。通过分析可以看出设计的疫苗储运箱不适合冬天或者冰冻天气，因为其采用的共晶板蓄冷剂为-5 ℃的共晶盐。在我国南方夏季具有较好的保温效果，可持续70 h左右，完全能够达到运输要求。

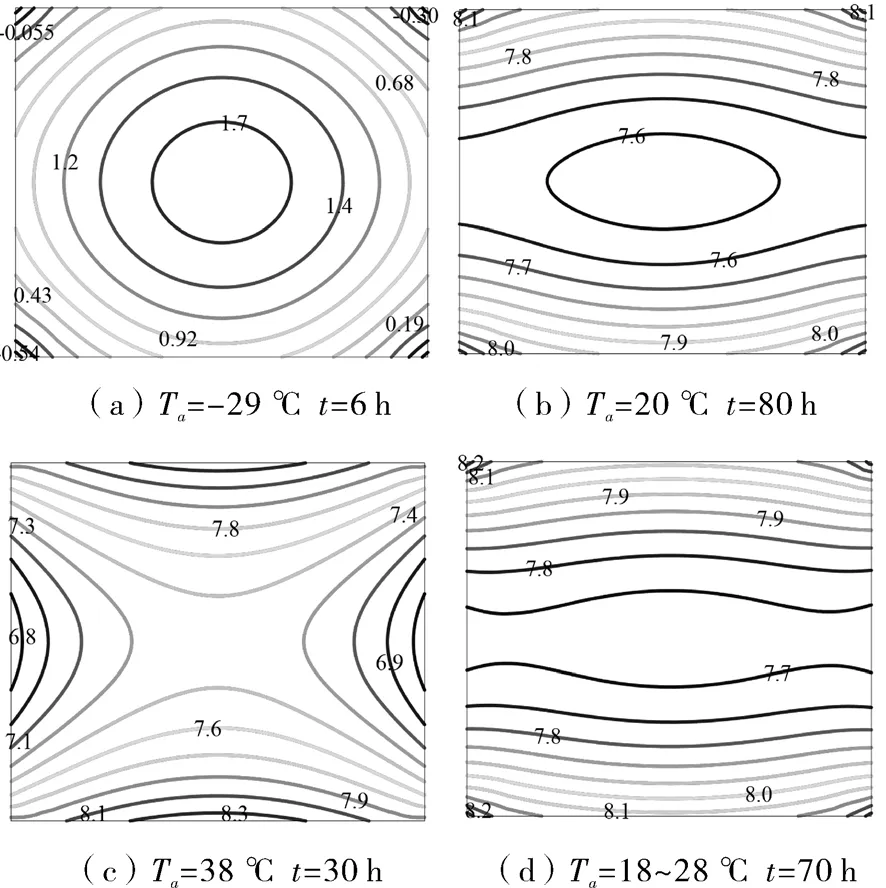
图3 不同环境温度下不同时刻疫苗包裹中截面温度场Fig.3 Cross section temperature field in vaccine package at different time under different ambient temperature

图4表示共晶板取不同厚度时，疫苗储运箱内不同位置的温度随时间变化情况。其中A线表示共晶板厚度为20 mm时疫苗包裹中心温度随时间变化情况，温度随着时间推移先上升后下降，之后持续上升，当时间t=65 h时，温度超过8 ℃，失去有效保护。D线表示共晶板厚度为30 mm时疫苗包裹中心处温度随时间变化情况，在72 h之内温度均未超出8 ℃。B线表示共晶板厚度为20 mm时疫苗包裹边角处温度随时间变化情况，温度先上升后下降再持续上升，在t=63 h时超过8 ℃。E线表示共晶板厚度为30 mm时疫苗包裹边角处温度随时间变化情况，在72 h之内均未超过8 ℃。A线和B线均先上升后下降，分析是因为开始时刻共晶板周围的空气温度较高，而共晶板并未起到冷却作用，周围空气的热量传至疫苗包裹，导致温度上升。C线和F线分别表示共晶板厚度为20 mm和30 mm时共晶板边角处温度随时间变化情况，温度从-5 ℃开始急剧上升一段时间后，上升速度逐渐变得缓慢。可以看出共晶板厚度越厚，各位置的温度越低，所以可以通过改变共晶板厚度的方式以满足不同地区、不同环境温度下疫苗的运输要求。

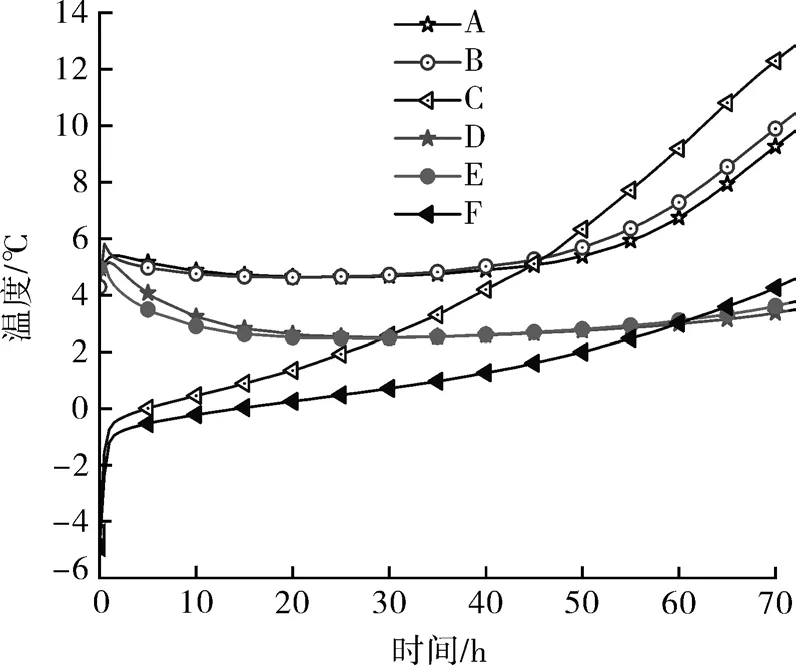
图4 不同共晶板厚度下不同位置温度变化曲线Fig.4 Temperature change curve of different positions under different thickness of eutectic plate

图5显示疫苗包裹温度最大值和最小值随时间变化的情况。当共晶板厚度为20 mm时，56 h后疫苗包裹的最大温度超过8 ℃。当共晶板的厚度为30 mm时，在14～36 h疫苗包裹温度低于2 ℃。共晶板厚度越厚，疫苗包裹的温度最大值和最小值均较低。

图5 疫苗包裹温度最大值和最小值随时间变化情况Fig.5 Variation of maximum and minimum temperature of vaccine package with time

图6显示考虑气温变化时疫苗储运箱各位置的温度变化情况，气温变化选取ISTA时变温度，共晶板的厚度取20 mm。可以看出疫苗包裹的温度总体呈上升趋势，但是随着气温存在波动情况。疫苗包裹在t=51 h时最高温度超过上限值8 ℃；在t=56 h时包裹平均温度超过上限值；在t=57.5 h时疫苗包裹的最小温度也超过上限值8 ℃。共晶板的平均温度，随着时间推移逐渐上升并且和疫苗包裹温度最大值趋于一致。在共晶板厚度为20 mm，考虑气温变化时，疫苗包裹的最低温度始终都不低于2 ℃。

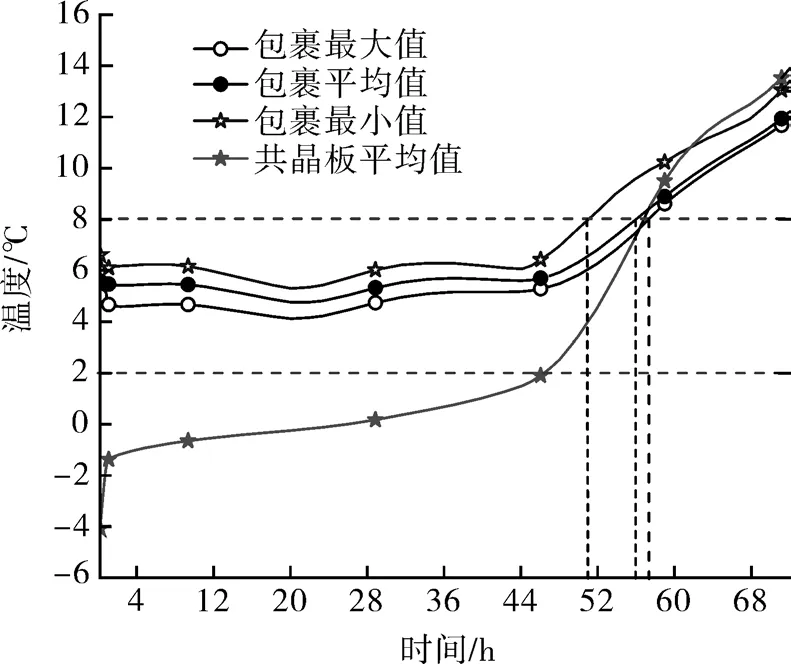
图6 考虑气温变化时储运箱的保温情况Fig.6 Thermal insulation of storage and transportation box considering temperature change

图7显示共晶板的厚度对有效储运极限时间的影响。图中3条线分别表示疫苗包裹内部最高温度极限时间、平均温度极限时间、最低温度极限时间。当共晶板厚度较薄时（L=10 mm），疫苗包裹最高温度在t=30 h时已经达到疫苗存储的最高温度8 ℃，平均温度在t=34 h时超过疫苗存储要求的最高温度，在t=35 h时整个疫苗包裹温度均超过储运要求的最高温度。随着共晶板厚度的增加，疫苗存储的有效时间持续增加，当共晶板的厚度达到35 mm时，最高温度在t=91 h时超过储运要求的最高温度，平均温度在t=92 h时超过储运要求的最高温度，最低温度在t=96 h时超过储运要求的最高温度。共晶板厚度越厚，疫苗存储低于要求最高温度的有效存储时间越长，可以通过调节共晶板厚度的方式来适应不同场景下的疫苗运输要求，但是共晶板厚度受到储运箱尺寸的限制。共晶板太厚容易导致疫苗运输过程中温度过低。当共晶板厚度为30 mm时，15～35 h疫苗包裹的最低温度略低于储运要求的最低温度2 ℃。

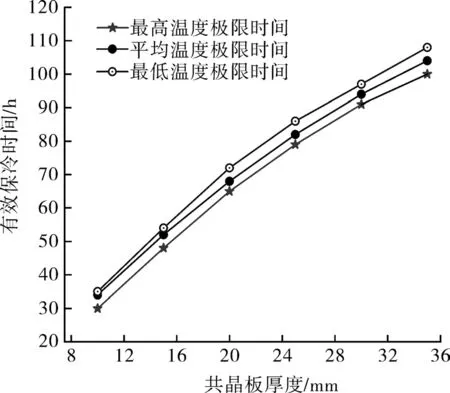
图7 共晶板厚度对保冷极限时长的影响Fig.7 Effect of eutectic plate thickness on cold insulation limit time

4 结语

本文针对疫苗运输需保持恒温的问题，设计一种基于共晶板蓄冷的疫苗储运箱，利用三维建模软件构建模型，建立相应的瞬态传热数理模型，分析其瞬态传热情况，通过研究发现，在疫苗储运箱其他参数确定的情况下，通过改变共晶板的厚度能有效地改变疫苗运输过程中的有效储运时间。本文研究结果可为不同场景下疫苗储运箱的设计及选择提供一定的依据。