妙用“四部曲” 让数学复习课重焕生机

☉葛扬芬

俗话说：“新授课育树，复习课育林”，一堂好的复习课，不仅能更好地帮助学生巩固知识，激发学生的学习主动性，还能开拓学生思维，丰富学生的知识经验，开发学生的创新潜能，最终使学生获得数学综合素养的发展。如何才能让复习课更有效，达到“温故而知新”的目的呢？文章将从以下四个方面出发，简要探讨促进小学数学复习课有效性的实践策略。

一、引导自主梳理，促进知识巩固

教师可以在复习课上，以错题为引，让学生进行自主整理或小组交流探讨，来达到查漏补缺的目的，从而更好地促进复习课的有效性。

例如，在进行“运算律”的复习课时，教师就可以先引导学生自主整理出这个单元内容中易出错的题目，并将此作为突破口，来帮助学生破解学习难点，收获更好的复习效果。师：“同学们，我们一起来回忆一下，之前我们学习了这个单元中的哪些内容？”生1：“有乘法和加法的结合律、交换律、分配律。”师：“没错，自己想一想在这个单元内容中哪些题目是经常会做错的？你们会怎么去复习和巩固这些错题呢？想好之后，从中选择一道你认为最经典的例题，来考考其他同学，并将自己完整的想法填写在学习单中。”生2：“我发现自己的错误主要集中在乘法分配律内容中，比如，96×25这道题目，之前总是不明白如何进行简算，现在经过复习，我知道了96 接近整百，可以转化成100-4，这样就变成了96×25=（100-4）×25，然后再利用乘法分配律进行计算，96×25=（100-4）×25=100×25-4×25=2400，这样很快就得出结果了，而且还不容易出错。”从上面这个例子中，可以看出复习课的主要目的之一就是查漏补缺，让学生自己进行整理，寻找自己的不足之处，并在错题的引领下，通过自主思考和复习，找到解决问题的有效方式，不仅能加深学生对错题的印象，避免重复错误的出现，还能使学生在自主复习中逐渐掌握正确的解题方法，加强对相关知识的理解和记忆，促进学生数学学习能力的提升。

二、巧用思维导图，建构知识网络

有效的复习课还需要重视知识的梳理与归纳，要帮助学生理清知识脉络，疏通各知识点之间的联系，建构完整的知识网络，并进一步引导学生在对旧知识的复习中探究到新知识的生长点，从而更好地完善和延伸学生的认知体系，拓宽学生的数学思维，让学生的思维走向更深处，促进学生数学学习能力的发展，也能更好地加强复习效果。［1］

例如，在进行“平面图形的面积”复习课时，教师可以这样引导学生复习。师：“同学们，你们还记得我们之前学过哪些平面图形的面积计算公式吗？”生1：“我们学过长方形、正方形、圆、三角形……”师：“那么，我们最先学的是哪个图形的面积计算公式？”生2：“是长方形。”师：“为什么先学这个图形？”生3：“因为长方形面积计算公式最简单也最容易记住。”生4：“不是的，因为正方形、平行四边形、圆这些图形面积计算公式是从它的基础上推导而来的，然后再由平行四边形面积推导出三角形和梯形面积计算公式。”生5：“因为这几种图形之间是密切联系的，其他图形的面积计算公式都是从长方形基础上延伸出来的。”师：“同学们说得非常棒，既然它们有着如此紧密的联系，大家是否能利用思维导图来将它们之间的关系展现出来呢？接下来，请大家组成合作小组一起来画一画，并交流想法。”于是，学生们纷纷投入到思维导图的创作中，并对小组作品进行了阐述，生6：“这是我们组的思维导图（如图1所示）。它很清晰地将推导过程展现了出来。我们都知道长方形面积计算公式是通过数方格得出的，而其他图形正如生4 所言是在长方形基础上推导得出。”生7：“这是我们组的思维导图（如图2所示）。正如生5 所言，这些图形之间是彼此相连的，事实上，三角形和梯形也可以从长方形基础上形成，因此，我们才这样画。”师：“大家画的思维导图都非常好，我们从中也发现了一种很重要的数学思想方法，就是转化思想，这也是数学中不可缺少的一种思想方法。”教师正是通过引导学生画思维导图的方式，来帮助学生理清知识脉络，逐渐建构起完整的知识网络，让学生逐渐领悟到数学思想方法，促进学生思维的纵深发展，收获更加良好的复习效果。

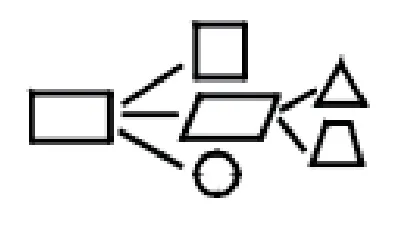
图1

图2

三、设计多元习题，增强数学应用

复习习题是复习课的重要内容之一，但在实际教学中，复习题往往都是比较单一、枯燥的，学生很难真正投入其中。因此，为了更好地提升复习课效率，教师应当优化复习习题，根据学生真实学情，设计多元化、典型性的习题，来激发学生的复习兴趣，帮助学生更好地梳理和巩固知识点。［2］

例如，在复习“解决问题的策略”这一内容时，教师就可以为学生设计以下生活化复习题：“周末，小明想去文具店买一些文具，但在购买的时候，小明发现自己带的钱只够买20 支圆珠笔或者5 本练习本，但是他两样都想买一点，最终，他选择购买了10 支圆珠笔，剩下的钱都购买练习本，请问他能买到几本练习本？”这类复习题与学生的生活非常贴近，不仅能够更好地提高学生的复习兴趣，还能充分调动学生的生活认知和经验，启发学生思维，帮助学生更加快速、准确地解决以上问题。再如，在复习“长方形的周长和面积计算公式”等知识时，教师也可以依据学生的真实学情，设计开放性的计算活动，让学生自己选择画一画或者摆一摆等方式来辅助解答。或者，教师也可以引导学生自己进行复习习题的设计。虽然很多学生设计的习题，存在着长方形面积过大或过小的问题，但是，这些都是学生自主思考和探究后的结果，能够更好地提高学生的复习积极性。同时，在开放性的习题中，学生们的数学应用能力也得到了充足的锻炼，为他们后续的数学学习铺垫了良好的基础。教师正是通过优化复习习题的方式，打破了以往复习题的单一模式，进一步激发了学生的复习兴趣，多角度开发了学生思维，也有效提升了复习课效率。

四、注重拓展延伸，发展思维深度

教师在进行复习课教学时，应更加具有针对性，要依据学生在学习上经常会出现的问题，以及教学重、难点问题，进行合理的复习规划，并在原有的知识基础上进行拓展延伸，提高学生的数学应用能力和知识应变能力，拓宽学生的数学思维，从而更好地促进学生数学学习能力和综合素养的提升。

例如，在进行“分数的意义”复习课时，教师可以先向学生展示这样一道题目：“有两根一样长的绳子，第一根剪掉米，第二根则剪掉，请问两根绳子哪一个剪掉的更多？”很明显这道题目需要分成三种情况进行分析，第一种：假如绳子的长度大于1 米，那么，第二根剪掉的更多；第二种：假如绳子的长度小于1 米，那么，第一根绳子剪掉的更多；第三种：假如绳子的长度正好是1 米，那么，两根绳子剪掉的一样多。随后，教师又向学生展示出了一道看起来与上一题没有什么差别的题目：“有一根绳子，第一次剪掉米，第二次则剪掉，正好全部剪掉，请问这根绳子哪一次剪掉的更多？”刚开始，学生们都受到惯性思维影响，毫不犹豫地也分成三种情况来分析，但是当学生们再次仔细阅读题目后就发现了两道题的差别：第一题是有两根一样长的绳子，而第二题则是一根绳子。于是，学生们又重新开始进行思考，逐渐明白到：第二题中的第一次剪掉米是一个具体的长度数量，应当占这根绳子的，因为第二次剪掉的是绳子的，正好全部剪完，因此，第一次剪的就是绳子的，很明显第二次剪的部分更多。这时，教师就可以继续追问：“假如将第二题中‘正好剪完’这个条件转变成还剩或米，大家知道如何去比较吗？或者索性直接将‘正好剪完’这个条件去掉，又应该如何解决呢？”伴随着问题的不断深入，学生们的思维也在不断拓展，更加深入理解了分数意义的本质。这样不仅有效拓展了学生思维的深度，还锻炼了学生的应变能力，促进了学生解决问题能力的发展。

总之，复习课不仅仅是帮助学生进行知识巩固的有效手段，更是促进学生发展、创新的重要助力。要想让复习课实现温故而知新，甚至创新的目的，教师不仅需要更新教育理念，还要探索各种有效策略，帮助学生进行知识梳理，完善知识结构，激发学生的创新潜能。这样，师生才能收获更加高效的复习效果。