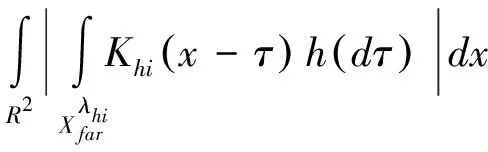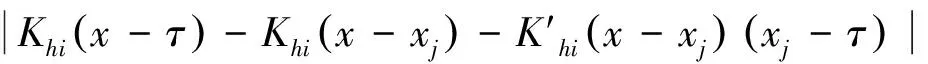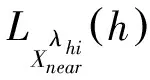二维带噪声超分辨率问题的研究
梁媛媛 王会敏 张天鹏 李 坤
(绍兴文理学院 数理信息学院,浙江 绍兴 312000)
0 引言
超分辨率,即通过软件或硬件提高原图的分辨率,在信号处理中至关重要,其应用领域包括光学成像[1]、天文学[2]、医学成像[3-4]和显微镜[5]等.目前,对无噪声超分辨率问题[6]的研究较多,常采用凸规划、梯度下降法等方法来解决此类问题.
在利用凸规划方法处理超分辨率[7-8]问题时,点源之间的距离必须满足最小分离条件Δ>2/fc.Denoyelle等[9]提出条件梯度法的改进算法,Boyds等[10]提出一种条件梯度法(CGM)的变体,但只适用于有限维信号.
另外,在处理超分辨率问题时,难以避免的噪声吸引了广大学者的注意.Donoho[11]研究了从光谱中恢复连续性度量问题.Fernandez[12]和Azais等[13]证明恢复的尖峰聚集在初始测量的Dirac测量周围.Fernandez[14]表明,当噪声水平相对于信号的振幅很小时,只要支集中元素之间的距离大于2/fc,通过求解凸规划问题,便可以解决噪声低通数据的点源叠加问题.Schiebinger等[15]对衍射极限超分辨率的理论分析证明,在理想情况下可以恢复任意接近的点源.Fernandez等[16]构造了一个准则,它为稀疏噪声情况下的光谱超分辨率提供了恢复保证.Candès,Fernandez[17]和Bernstein等[18]表明处理带噪声的一维超分辨率的方法可以扩展到多维,但均未给出详细的过程.
本文推广了Emmanuel构造的低频多项式,采用TV范数最小化方法研究二维带噪声的超分辨率问题.结果表明,当点源之间的距离满足最小分离条件时,估计误差与噪声水平及超分辨率因子的平方成正比.
1 预备知识
1.1 超分辨率问题与模型
将二维带噪声的超分辨率问题建模为
y(x)=(Qlos)(x)+ξ(x)
(1.1)
其中x=(t,u)是在平面空间[0,1]2中的连续参数(位置、频率等),噪声ξ(x)可以是随机的也可以是确定的,Qlo是截止频率为flo=1/λlo的带限算子,λlo是周期.
下面对点源叠加问题进行建模
其中xj是平面空间[0,1]2中的点,δxj是在xj处的Dirac测量,振幅aj可以是复值.
希望在更精细的尺度λhi≪λlo上处理信号s,即得到一个满足Qhisest≈Qhis的高分辨率估计sest,其中Qhi与Qlo的定义相似.换言之,在已知低频光谱[-flo,flo]的噪声数据的情况下,希望估计更宽的频谱[-fhi,fhi].下面定义超分辨率因子SRF
简而言之,如果SRF等于N,则希望分辨率为原来的N倍.目标是了解在λhi上估计信号与真实信号Khi(sest-s)之间的误差与噪声水平及SRF的关系.
1.2 用凸规划方法对模型求解
假设模型(1.1)中的x∈[0,1]2,ξ(x)是一个带限测量误差项且满足

(1.2)
误差ξ(x)可以是任意的,也可以是对抗的.
具体地,设Klo为周期的Dirichlet核

为了恢复信号,求解凸问题

(1.3)

2 主要结果
2.1 最小分离条件
目标是近似信号,直到达到一定的分辨率,该分辨率由计算误差的平滑核λhi>λlo的宽度决定.为了达到此目标,设
是具有截止频率fhi=1/λhi的Ferjer内核.
无论使用哪种方法来实现超分辨率,都必须引入一个关于信号支集的条件,以防止点源过于聚集[19].下面,在定义中给出关于二维信号的最小分离概念及噪声水平,在定理中给出估计误差与噪声水平及SRF之间的关系.
定义2.1(最小分离) 对于点族J∈R2,J中两个元素的对应变量之间的最小距离
称为最小分离,其中σt,σu是内核在t,u处的标准差,(1.2)表明,低分辨率误差服从
‖Klo*(sest-s)‖L1≤δ.
定理2.1 假设s的支集J服从分离条件
Δ(J)≥2λlo
则在噪声模型(1.2)中,存在一个常数C0>0,使得问题(1.3)的任何解sest都满足
‖Khi*(sest-s)‖L1≤C0SRF2δ.
为了简单起见,分析问题(1.3)和噪声的有界L1范数.例如,假设观察到有噪声的频谱样本为
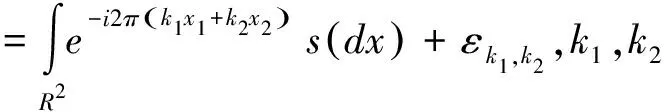
=-flo,-flo+1,…,flo
(2.1)
其中εk1,k2为复值N(0,σ2)变量上的独立同分布序列,这等价于一个具有加性高斯白噪声的线谱估计问题.为了对该模型下的信号进行求解,提出以下凸优化方法
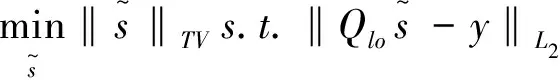
(2.2)

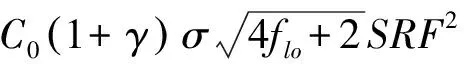
的概率至少为1-e-2floγ2.
2.2 高分辨率内核的界
为了证明定理2.1,需要给出Ferjer核及其导数的界


(2.3)

(2.4)
其中C0、C1和C2是独立于λhi的正常数,f:[0,1/2]→R2是非负递增函数.
3 证明
令J={xj}是s的支集,x∈R2,并定义互不相交的子集


令h=s-sest,则误差遵循
‖Qloh‖L1≤‖Qlos-y‖L1+‖y-Qlosest‖L1≤2δ
由‖h‖TV≤‖s‖TV+‖sest‖TV≤2‖s‖TV知TV范数有界,目标是约束平滑误差e:=Khi*h

在证明定理2.1时,需要对h的TV范数做出限制,这在引理3.1中给出.而在应用引理3.1中的边界时,需要控制测度值h在一个常数和一个线性函数上的局部作用,这些局部界将在引理3.2和引理3.3中给出.
引理3.1 在定理2的条件下,存在Ca>0和,Cb>0满足
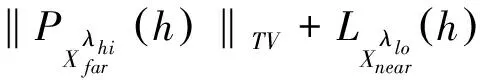

引理3.2 在定理2的条件下,且测度h满足‖Qloh‖L1≤2δ,则

引理3.3 在定理2的条件下,且测度h满足‖Qloh‖L1≤2δ,则

3.1 证明思路
引理3.1、3.2和3.3的证明,均依赖于引理3.4中构造的低频多项式,此多项式是对引理2.4[17]中的多项式的推广.引理3.2的证明还依赖于当x接近支集的任何元素时,b(x)所选择的符号模式,这在引理3.5给出.
本节分别在3.1.1节及3.1.2节中证明了引理3.1和引理3.2.由于篇幅有限,文中省略了引理3.3及引理3.5的证明,引理3.3的证明与引理3.2的证明思路相似,引理3.5的证明可参照附录A[17]和3.3[18],将一维信号改为二维信号即可.

满足
b(xj)=vj,xj∈J
(3.1)

(3.2)

(3.3)
其中Ca,Cb是常数,且0 引理3.5 存在一个低频多项式b(x)满足引理3.4中的性质,另外 3.1.1 证明引理3.1 证明 应用定理6.12的推论[20],对PJh进行极分解 PJh=eiφ(x)|PJh| 其中φ(x)是定义在R2上的实函数,令vj=e-iφ(xj),因为b是低频的, (3.4) 由于b在J上插入e-iφ (3.5) (3.6) (3.7) 将式(3.6)和式(3.7)代入到(3.5)的最后一个不等式右侧可以得到 类似地,有 3.1.2 证明引理3.2 证明 考虑极分解 其中θj∈[0,2π).设引理3.4中的vj=eiθj,由三角不等式得 (3.8) 对所有的xj∈J,由三角不等式和(3.4)知 (3.9) 其中第二项由引理3.5中的xj=(0,0)得到,将(3.9)代入(3.8)得 首先应用三角形不等式得到一个关于‖e‖L1的界 (3.10) (3.11) 为了约束(3.10)第二个不等式右侧的第二项,利用在xj附近的ψ(τ)=Khi(x-τ)的Taylor级数展开所得到的超分辨率核的一阶近似,则对于任何满足|τ-xj|≤ωλhi的τ 不失一般性,设xj=(0,0),结合三角不等式,得 (3.12) 再次将Fubini定理与(2.3)相结合,得到 (3.13) (3.14) (3.15) 由(2.3)和(2.4)得 (3.16) 对于一个常数C4>0,结合Fubini定理,得 (3.17)





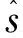
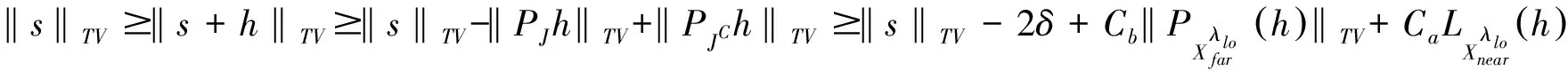





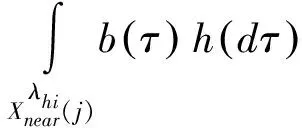


3.2 证明定理2.1