计及转速平滑恢复的双馈风电机组自适应频率控制策略
杨德健,许益恩,高洪超,郑太英,金恩淑
计及转速平滑恢复的双馈风电机组自适应频率控制策略
杨德健1,许益恩2,高洪超3,郑太英4,金恩淑1
(1.现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学),吉林 吉林 132012;2.南通大学电气工程学院,江苏 南通 226019;3.清华大学电机工程与应用电子技术系,北京 100084;4.浙江大学电气工程学院,浙江 杭州 310058)
为解决现有双馈风电机组频率控制策略不能充分利用转子动能支撑电网频率及风机转速恢复造成的二次频率冲击问题,提出了一种计及转速平滑恢复的双馈风电机组自适应频率控制策略。首先在电网频率支撑阶段,借助指数函数将风电机组频率控制系数和电网频率偏差建立耦合关系,使频率控制系数随频率偏差增加而变大,从而使风电机组在频率支撑阶段释放更多能量,提高频率最低点;其次在风机转速恢复阶段,借助一次递减函数在预设时间内将控制系数平滑减少至零,实现可控的转速恢复,同时消除转速恢复对频率的二次冲击。最后,通过EMTP-RV软件搭建了IEEE 4机2区域的电力系统模型,验证了所提策略的有效性。
双馈风电机组;频率响应;平滑转速恢复;自适应控制
0 引言
随着“碳达峰,碳中和”战略的提出,新能源发电发展迅速,我国电网中包括风电、光伏等新能源发电比重不断增加,以新能源为主体的新型电力系统成为我国电力系统发展的必然趋势[1-2]。风电凭借分布范围广、开发成本较低、发电技术较成熟等优势,在新能源发电中占据重要地位[3-5]。为实现有功与无功解耦、最大功率追踪(Maximum Power Point Tracking, MPPT)等高级控制策略,双馈风力发电机组(Doubly-Fed Induction Generator, DFIG)借助电力电子器件接入到电网中,导致其转速与电网频率解耦,从而造成电力系统整体惯性水平和一次调频能力下降[6]。在电网发生扰动后电网最大频率偏差增大,随着风电渗透率的日益提高,该现象将愈发严重[7-9]。若电网频率跌落至阈值49 Hz以下,电力系统第三道防线“低频减载”保护机制启动,切除部分负载,防止电网崩溃[10]。由此可见,规模化风电并网后电力系统的频率稳定性势必会面临巨大的挑战,这使得DFIG主动参与系统调频已然成为当今研究热点之一[11-12]。
风机通过超速控制、变桨控制及两者协调控制策略可为系统频率调节留有一定的有功备用[13-15]。文献[13]提出了一种惯量控制和变桨控制相结合的控制策略,有效改善了系统频率的稳态特性,但实际运行中,桨距角的频繁动作会加重风机的机械疲劳,缩短变桨系统寿命。文献[14]采用超速控制与虚拟惯量控制协同控制策略参与系统调频,虽然该方法有利于延长风机变桨系统寿命,然而风机长期运行于减载模式,缩小了转速调节范围,弱化了高频扰动下风机调频能力,且不利于风电场的经济运行。
此外,DFIG可通过释放转子动能参与系统调频,其调频过程主要包含频率支撑和转速恢复两个阶段。在频率支撑阶段,鉴于风机转子具有快速吞吐动能的能力,因此,最常见的控制方法是在转子侧控制器中附加频率控制回路,模拟常规同步机组的惯性响应和一次调频特性,即比例微分(PD)虚拟惯量控制,实现DFIG主动参与系统调频[16]。由于D控制器对频率微分量敏感,本文主要介绍风机参与一次调频,因此将PD控制器简化为P控制器。文献[17]通过附加P控制器到转子侧控制回路中,实现了DFIG参与系统调频,提高了频率最低点,然而该策略采用固定频率控制系数,限制了不同风速下DFIG的调频潜力及低转速下易引起风机失速。为此,文献[18]提出了基于风机有效旋转动能的变系数频率控制策略,充分挖掘了不同风速下风机的调频潜力,同时有效预防了风机失速现象。然而上述研究主要侧重于风机自身运行状态,对于不同扰动场景下风机调频特性的研究不足。
DFIG利用转子动能参与电力系统调频后,风机转速会偏离MPPT运行所对应的最优转速,弱化了风能捕获效率,不利于风电场的经济运行。文献[19]提出基于有功功率阶跃式变化的转速恢复策略,但由于风机有功出力突变,导致了严重的频率二次跌落,在高风电渗透水平下,甚至低于频率最低点。为此,文献[20]提出风机有功出力“斜坡”衰减的控制策略,在一定程度上缓解了二次频率跌落,但延迟了转速恢复时间,进一步影响了风机捕获风能。文献[21]借助恒定加速功率来驱动风机转速恢复,然而该方法需要的机械输入功率很难直接测量。文献[22]借助储能装置,在消除二次频率跌落的同时,实现了转速快速恢复,然而由于储能装置系统成本较高,对服务于频率与转速恢复控制,大规模配置并不经济。文献[23]提出了基于逻辑回归函数的变系数下垂控制,实现了平滑的恢复转速,但采用频率微分量作为控制输入,受噪音影响大。此外,该方法整定的参数偏多,给实际工程应用增加困难。
针对上述问题,本文提出了一种计及转速平滑恢复的DFIG自适应频率控制策略。该策略在现有基于风机有效旋转动能的控制策略的基础上加以改进,首先在电网频率支撑阶段,借助指数函数将频率控制系数与电网频率偏差建立耦合关系,使得DFIG在不同场景下充分利用转子动能为电网提供优质的频率响应服务。其次在转速恢复阶段,借助一次递减函数,使控制系数在预设时间内平滑衰减至零,使得DFIG平稳切换至MPPT运行模式,从而在实现平稳可控的转速恢复的同时,消除了转速恢复对电网的二次频率冲击。最后,基于EMTP-RV搭建了含DFIG的电力系统模型,在不同风速和扰动场景下,验证了所提频率控制策略的有效性。
1 DFIG运行特性
本节简要介绍DFIG的结构及其控制系统,其中,DFIG控制系统由转子侧变流器控制器和网侧变流器控制器组成:转子侧变流器控制器负责调节输入到电网的有功和无功功率;网侧变流器控制器用于维持直流环节(DC-Link)电压的稳定。图1给出了典型双馈风力发电机组结构。
1.1 风力机模型
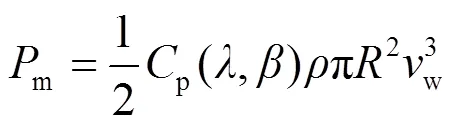

图1 典型双馈风力发电机组结构
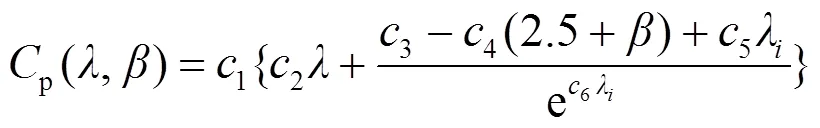
其中,
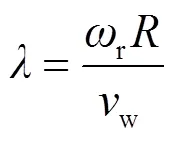

1.2 MPPT控制
DFIG运行在MPPT控制模式时,其输出参考功率MPPT为[24]
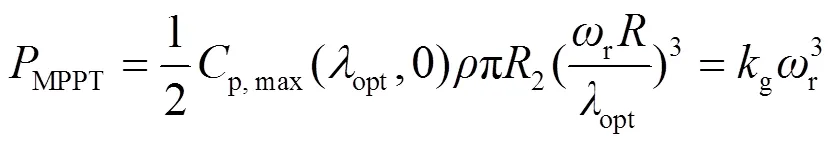
其中,
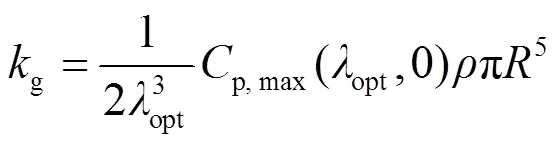
2 电网频率动态指标的机理分析
根据文献[25],系统频率响应(System Frequency Response, SFR)模型为
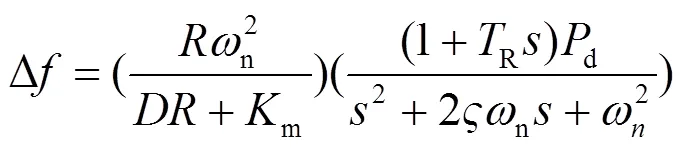
对式(7)进行拉氏反变换,可得系统频率偏差时域的表达式

对式(8)求导可得

其中,

(2) 在转速恢复阶段,根据能量守恒定律,DFIG通过减少有功出力,可实现其转速恢复,然而有功出力阶跃式地减少会造成系统短时有功缺额,即Δ增大,从而导致严重的电网频率二次冲击。
综上,通过设计合理的DFIG频率控制策略可有效缓解电网频率的最大偏差、变化率以及风机转速恢复对系统频率的二次冲击。
3 DFIG频率控制策略
本节将分别介绍现有DFIG频率控制策略和改进后的频率控制策略。
3.1 现有DFIG频率控制策略
图2给出了现有频率控制策略的原理图。此时,DFIG频率控制回路有功出力为

式中,为频率控制系数。

由于上述策略采用的频率控制系数为固定值,限制了不同风速下DFIG的调频潜力。为此,文献[18]提出了基于DFIG有效旋转动能的变系数频率控制,其频率控制系数的表达式为

3.2 计及转速平滑恢复的自适应频率控制策略
针对上述问题,本文分别在频率支撑阶段和转速恢复阶段整定与电网频率偏差耦合的控制系数以及时变控制系数,构建了一种计及转速平滑恢复的自适应频率控制策略,其逻辑结构如图3所示。
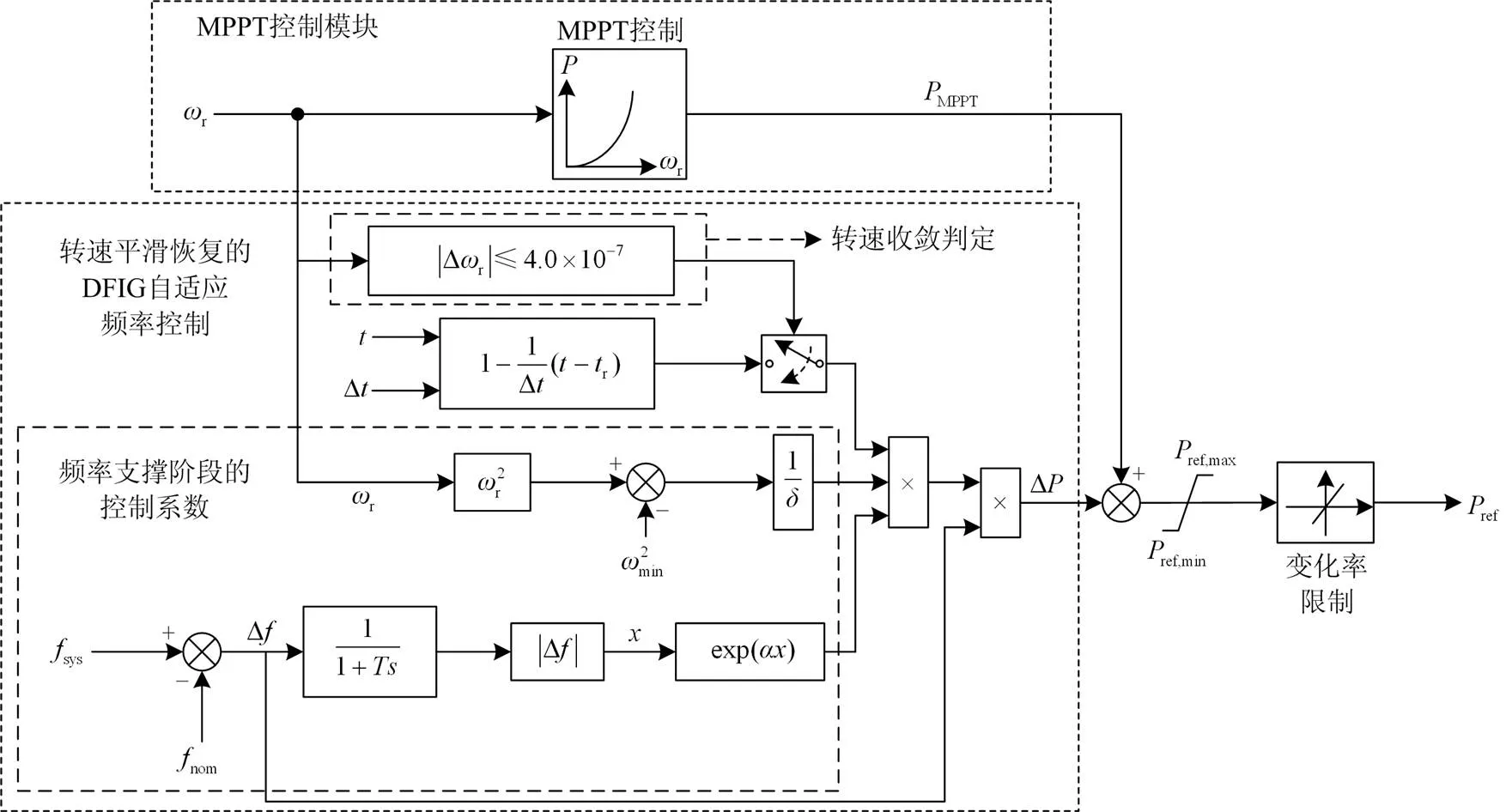
图3 计及转速平滑恢复的DFIG自适应频率控制策略
下面将分别对所提频率控制策略中频率支撑阶段和转速恢复阶段的控制系数的整定进行详细阐述。
3.2.1频率支撑阶段的控制系数sup
如图3所示,本文借助指数函数将频率控制系数与电网频率偏差建立耦合关系,得到电网频率支撑阶段的频率控制系数sup,其表达式如式(14)所示。

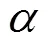
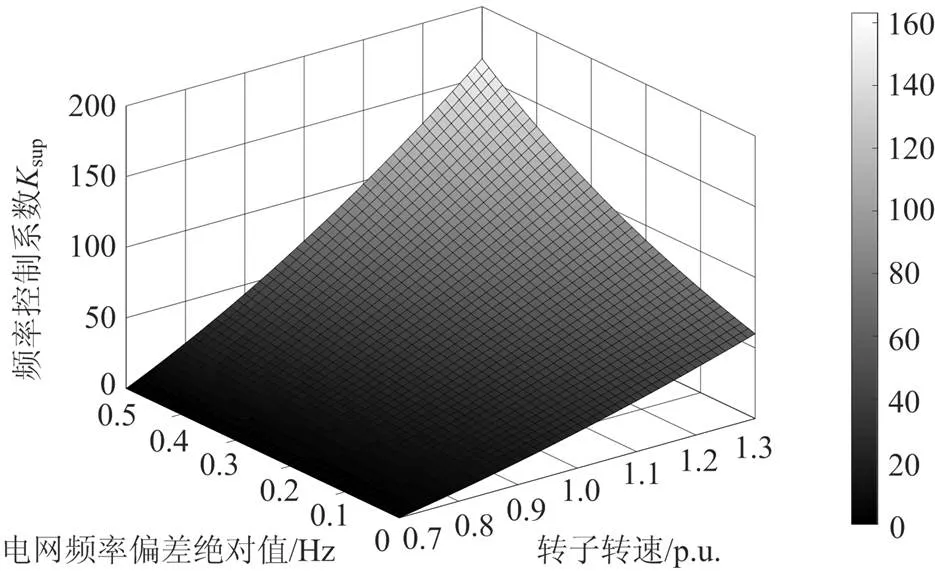
图4 频率支撑阶段的控制系数
从图4中可以看出,在扰动初期,控制系数主要根据转速变化;随着电网频率偏差∆逐渐增大,关于电网频率偏差的指数函数起决定性作用,即频率控制系数sup随电网频率偏差的增加而变大,从而使DFIG释放更多的能量参与系统调频,减小最大频率偏差。
3.2.2转速恢复阶段的控制系数rec
在电网频率支撑阶段,由于DFIG输出电磁功率大于输入机械功率,DFIG转子转速持续下降,并伴随其有功出力减少。根据摇摆方程式可知,当输出电磁功率与输入机械功率相等时,风机转速收敛。在文献[22]中,若DFIG转子转速满足式(15),则可判定其转速收敛。

式中:为DFIG转子转速的采样周期,采样周期为260ms。
为恢复风机转速,本文基于“时变”的控制思想,使控制系数及有功增量在预设时间内平滑衰减至零,从而使DFIG有功出力平稳切换至MPPT控制模式,实现平稳可控的转速恢复。
综上,本文在控制系数sup的基础上乘以一个随时间逐渐递减的一次函数,得到转速恢复阶段控制系数rec。其表达式如式(16)所示。
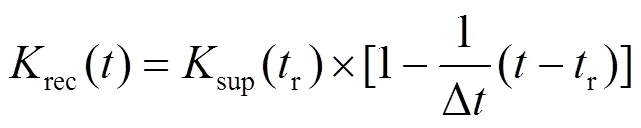
式中:tr为DFIG转子转速收敛对应时刻;Δt为转速恢复阶段持续时间。
4 算例分析
如图6所示,为了验证所提策略的有效性,本文在EMTP-RV仿真软件上搭建了IEEE 4机2区域系统进行仿真验证。该系统包含一个风电场、4台同步发电机组及静负荷。

图6 IEEE 4机2区域系统
下面将在风电渗透率为20%,风速分别为7.5 m/s和9.5 m/s的场景下,对DFIG采用MPPT控制、基于DFIG有效旋转动能的变系数频率控制(现有方法)及本文提出的频率控制策略(优化方法)时的控制效果进行分析与对比。具体算例如表1所示。

表1 算例设置
此外,DFIG的基础调差系数为2%,电网频率性能调节因子设为100,DFIG转子转速恢复时间Δ设为15 s。
在40 s时,预设同步机组SG3脱机作为本次仿真的扰动事件。图7、图8与图9分别给出了算例1—3在上述三种不同控制策略下的仿真结果。
4.1 不同扰动的仿真分析
由于不同扰动下,电网频率偏差存在差异。为验证不同扰动下优化方法的有效性,本节将结合算例1和算例2分别研究同步机组有功出力损失50 MW和90 MW情况下各控制策略的调频性能。
4.1.1算例1——有功出力损失50 MW
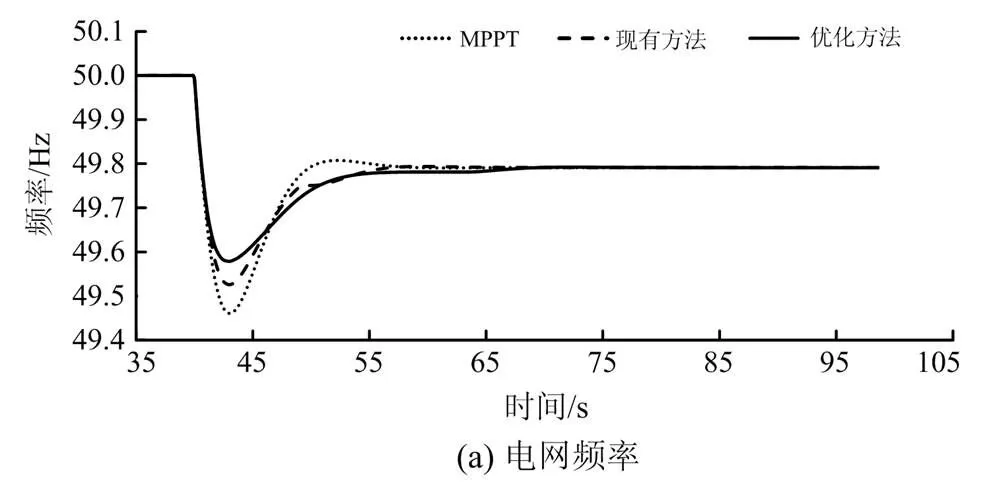
由图7(a)可知,DFIG采用MPPT控制时,无法为电网频率提供支撑,电网频率最低点为49.711 Hz。当DFIG采用现有方法时,电网频率的最低点增加至49.748 Hz,其原因是DFIG向电网中注入了一定的旋转动能,有功功率增加至43 MW,如图7(b)所示。随着DFIG转速收敛,为恢复转速,在49.920 s时,DFIG有功功率直接减少3 MW,导致频率发生二次跌落,跌落值为49.873 Hz。当DFIG采用优化方法时,电网频率最低点进一步增加至49.764 Hz,这主要是因为在频率支撑阶段,优化方法的控制系数与电网频率偏差耦合,且随频率偏差增加而变大,DFIG短时有功出力更大,有功功率增加至46 MW,如图7(b)所示。在转速收敛阶段,该方法借助一次递减函数使得DFIG控制系数和有功出力在15 s内平滑衰减至零,实现了平稳可控的转速恢复,同时有效地消除了频率的二次跌落。


图7 算例1的仿真结果
4.1.2算例2——有功出力损失90 MW
由图8(a)可知,受大功率脱机影响,电网频率跌落严重,DFIG不参与调频时,电网频率最低点进一步跌落至49.459 Hz,低于算例1。当DFIG采用现有方法和优化方法时,电网频率分别在43.021 s和43.031 s时达到最低点,分别为49.525 Hz和49.578 Hz,这主要是因为优化方法中DFIG向电网注入了更多的有功;此外,调频结束后,如图8(b)所示,由于现有方法借助有功功率阶跃变化驱动转速恢复,系统频率不可避免地发生了二次下跌;而优化方法则得到了与算例1相似的转速恢复效果。
由上述两种算例分析可知,在不同扰动场景下,采用本文提出的频率控制策略,可进一步提高电网频率最低点,同时实现转速平滑恢复。
4.2 风速的影响
由于sup与转速呈正相关,从而影响DFIG的瞬时有功出力,为验证不同风速下优化方法的有效性,本节将研究风速为9.5 m/s时各控制策略的调频性能。

从仿真结果可知,受风速影响,扰乱前DFIG有功出力增加至74 MW。从图9(a)中可知,现有方法中电网频率最低点提高了0.149 Hz,优化方法提高了0.219 Hz,而算例2中现有方法仅提高了0.066 Hz,优化方法提高了0.119 Hz,由此可见,在高风速场景下优化方法和现有方法的调频效果优于算例2。此外,与现有转速恢复方法相比,优化方法依然可做到转速平稳恢复且电网频率变化平缓,无较大的频率波动。
5 结论
本文针对现有DFIG频率控制策略不能充分利用转子动能支撑电网频率及风机转速恢复造成的二次频率冲击问题,提出了一种计及转速平滑恢复的DFIG自适应频率控制策略,其特点如下:
(1) 在频率支撑阶段,借助指数函数将DFIG频率控制系数和电网频率偏差建立耦合关系,使控制系数随频率偏差增加而变大,实现了“先抑后扬”的调频效果,解决了现有频率控制策略不能充分利用风机转子动能支撑电网频率的问题。
(2) 在转速恢复阶段,借助一次递减函数在预设时间内将控制系数和有功出力平滑减少至零,从而实现平稳可控的DFIG转速恢复的同时,解决频率二次跌落问题。
仿真结果表明,本文所提控制策略在不同扰动和风速场景下均能有效提高DFIG频率响应能力,同时平滑转速恢复过程及消除频率二次跌落。
[1] 卓振宇, 张宁, 谢小荣, 等. 高比例可再生能源电力系统关键技术及发展挑战[J]. 电力系统自动化, 2021, 45(9): 171-191.
ZHUO Zhenyu, ZHANG Ning, XIE Xiaorong, et al. Key technologies and developing challenges of power system with high proportion of renewable energy[J]. Automation of Electric Power Systems, 2021, 45(9): 171-191.
[2] 赵东元, 胡楠, 傅靖, 等. 提升新能源电力系统灵活性的中国实践及发展路径研究[J]. 电力系统保护与控制, 2020, 48(24): 1-8.
ZHAO Dongyuan, HU Nan, FU Jing, et al. Research on the practice and road map of enhancing the flexibility of a new generation power system in China[J]. Power System Protection and Control, 2020, 48(24): 1-8.
[3] 陈国平, 董昱, 梁志峰. 能源转型中的中国特色新能源高质量发展分析与思考[J]. 中国电机工程学报, 2020, 40(17): 5493-5506.
CHEN Guoping, DONG Yu, LIANG Zhifeng. Analysis and reflection on high-quality development of new energy with Chinese characteristics in energy transition[J]. Proceedings of the CSEE, 2020, 40(17): 5493-5506.
[4] 卢一菲, 陈冲, 金成日, 等. 直驱永磁风电机组高电压穿越协调控制策略[J]. 电力系统保护与控制, 2020, 48(15): 50-60.
LU Yifei, CHEN Chong, JIN Chengri, et al. HVRT coordinated control strategy of a direct-driven PMSG[J]. Power System Protection and Control, 2020, 48(15): 50-60.
[5] MENSOU S, ESSADKI A, NASSER T, et al. A direct power control of a DFIG based-WECS during symmetrical voltage dips[J]. Protection and Control of Modern Power Systems, 2020, 5(1): 36-47.
[6] 王同森, 程雪坤. 计及转速限值的双馈风机变下垂系数控制策略[J]. 电力系统保护与控制, 2021, 49(9): 29-36.
WANG Tongsen, CHENG Xuekun. Variable droop coefficient control strategy of a DFIG considering rotor speed limit[J]. Power System Protection and Control, 2021, 49(9): 29-36.
[7] 李军徽, 冯喜超, 严干贵, 等. 高风电渗透率下的电力系统调频研究综述[J]. 电力系统保护与控制, 2018, 46(2): 163-170.
LI Junhui, FENG Xichao, YAN Gangui, et al. Survey on frequency regulation technology in high wind penetration power system[J]. Power System Protection and Control, 2018, 46(2): 163-170.
[8] BAO W, WU Q, DING L, et al. A hierarchical inertial control scheme for multiple wind farms with BESSs based on ADMM[J]. IEEE Transactions on Sustainable Energy, 2021, 12(2): 751-760.
[9] 王瑞明, 徐浩, 秦世耀, 等. 风电场一次调频分层协调控制研究与应用[J]. 电力系统保护与控制, 2019, 47(14): 50-58.
WANG Ruiming, XU Hao, QIN Shiyao, et al. Research and application on primary frequency regulation of wind farms based on hierarchical coordinated control[J]. Power System Protection and Control, 2019, 47(14): 50-58.
[10] 高翔. 现代电网频率控制应用技术[M]. 北京: 中国电力出版社, 2010.
[11] 付华, 刘公权, 齐晨飞, 等. 计及微电网黑启动的虚拟同步发电机调频策略[J]. 电力系统保护与控制, 2020, 48(14): 59-68.
FU Hua, LIU Gongquan, QI Chenfei, et al. Frequency regulation strategy of a virtual synchronous generator-based microgrid considering the black start process[J]. Power System Protection and Control, 2020, 48(14): 59-68.
[12] 黄杰杰, 李生虎, 孙婷婷. 基于改进动态潮流的 DFIG 风电系统层级频率模型预测控制[J]. 电力系统保护与控制, 2020, 48(22): 68-75.
HUANG Jiejie, LI Shenghu, SUN Tingting. Hierarchical frequency control for a power system with DFIG based on frequency prediction with improved dynamic power flow[J]. Power System Protection and Control, 2020, 48(22): 68-75.
[13] 王济菘, 陈明亮. 虚拟惯量配合变桨控制的风机一次调频实验研究[J]. 电测与仪表, 2019, 56(23): 18-23.
WANG Jisong, CHEN Mingliang. An experimental study on primary frequency regulation of D-PMSG with virtual inertia and pitch control[J]. Electrical Measurement & Instrumentation, 2019, 56(23): 18-23.
[14] 蔡国伟, 钟超, 吴刚, 等. 虑风电机组超速减载与惯量控制的电力系统机组组合策略[J]. 电力系统自动化, 2021, 45(16): 134-142.
CAI Guowei, ZHONG Chao, WU Gang, et al. Unit commitment strategy of power system considering overspeed load reduction and inertia control of wind turbine [J]. Automation of Electric Power Systems, 2021, 45(16): 134-142.
[15] ZERTEK A, GREGOR V, MILOŠ P. A novel strategy for variable-speed wind turbines’ participation in primary frequency control[J]. IEEE Transactions on Sustainable Energy, 2012, 3(4): 791-799.
[16] WANG S, TOMSOVIC K. Fast frequency support from wind turbine generators with auxiliary dynamic demand control[J]. IEEE Transactions on Power Systems, 2019, 34(5): 3340-3348.
[17] VAN DE VYVER J, DE KOONING J, VANDEVELDE L, et al. Droop control as an alternative inertial response strategy for the synthetic inertia on wind turbines[J]. IEEE Transactions on Power Systems, 2016, 31(2): 1129-1138.
[18] HU Y, WU Y. Approximation to frequency control capability of a DFIG-based wind farm using a simple linear gain droop control[J]. IEEE Transactions on Industry Applications, 2019, 55(3): 2300-2309.
[19] ULLAH N R, THIRINGER T, KARLSSON D. Temporary primary frequency control by variable speed wind turbines—potential and application[J]. IEEE Transactions on Power Systems, 2008, 23(2): 601-612.
[20] EL ITANI S, ANNAKKAGE U D, JOOS G. Short-term frequency support utilizing inertial response of DFIG wind turbines[C] // 2011 IEEE Power and Energy Society General Meeting, July 24-28, 2011, Detroit, MI, USA: 1-8.
[21] XU G, XU L. Improved use of WT kinetic energy for system frequency support[J]. IET Renewable Power Generation, 2017, 11(8): 1094-1100.
[22] 赵晶晶, 李敏, 何欣芹, 等. 基于限转矩控制的风储联合调频控制策略[J]. 电工技术学报, 2019, 34(23): 4982-4990.
ZHAO Jingjing, LI Min, HE Xinqin, et al. Coordinated control strategy of wind power and energy storage in frequency regulation based on torque limit control[J]. Transactions of China Electrotechnical Society, 2019, 34(23): 4982-4990.
[23] 劳焕景, 张黎, 宋鹏程, 等. 一种考虑最优状态动态恢复的风电持续调频策略[J]. 电网技术, 2020, 44(12): 4504-4512.
LAO Huanjing, ZHANG Li, SONG Pengcheng, et al. Wind power sustained frequency regulation strategy with dynamic optimized state recovery behavior[J]. Power System Technology, 2020, 44(12): 4504-4512.
[24]YANG D, KIM J, KANG Y, et al. Temporary frequency support of a DFIG for high wind power penetration[J]. IEEE Transactions on Power Systems, 2018, 33(3): 3428-3437.
[25] SHI Q, LI F, CUI H. Analytical method to aggregate multi-machine SFR model with applications in power system dynamics studies[J]. IEEE Transactions on Power Systems, 2018, 33(6): 6355-6367.
Self-adaptive frequency control scheme of a doubly-fed induction generator with smooth rotor speed recovery
YANG Dejian1, XU Yien2, GAO Hongchao3, ZHENG Taiying4, JIN Enshu1
(1. Key Laboratory of Modern Power System Simulation and Control & Renewable Energy Technology Ministry of Education (Northeast Electric Power University), Jilin 132012, China; 2. College of Electrical Engineering, Nantong University, Nantong 226019, China; 3. Department of Electrical Engineering, Tsinghua University, Beijing 100084, China;4. College of Electrical Engineering, Zhejiang University, Hangzhou 310058, China)
The existing frequency control method of doubly-fed induction generators (DFIGs) is unable to fully use the rotor rotational energy to support the frequency and a secondary frequency drop is caused during the rotor speed recovery of the DFIG. To address these issues, this paper suggests a self-adaptive frequency control scheme of a DFIG with smooth rotor speed recovery. First, during the frequency support stage, the coupling relationship between the droop control coefficient of DFIGs and the frequency deviation is established using the exponential function so that the control coefficient becomes large with the increasing frequency deviation. DFIGs can release more rotational energy to the power grid and then improve the frequency nadir. Secondly, during the speed recovery stage, the control coefficient gradually decreases to zero within the preset period by using the first-order decreasing function so as to achieve controllable rotor speed recovery and remove the secondary frequency drop. Finally, an IEEE 4-machine 2-area power system model is modeled using an EMTP-RVsimulation to illustrate the effectiveness of the proposed frequency control scheme.
This work is supported by the National Natural Science Foundation of China (No. 51877112).
DFIG; frequency control; smooth rotor speed recovery; self-adaptive control
10.19783/j.cnki.pspc.210941
国家自然科学基金项目资助(51877112);江苏省高校自然科学基金项目资助(20KJB470026)
2021-07-21;
2021-09-10
杨德健(1990—),男,博士,研究方向为风力发电并网控制技术;E-mail: dejian@ntu.edu.cn
许益恩(1998—),男,通信作者,硕士,研究方向为风力发电并网控制技术。E-mail: 2011310014@stmail.ntu.edu.cn
(编辑 张爱琴)

