基于灰色系统理论的测控设备状态预测算法研究
张 垚,吴宗清,严亚龙,付树洪
(中国西安卫星测控中心宇航动力学国家重点实验室 西安 710043)
引言
自1982 年我国邓聚龙教授首次提出关于灰色系统控制问题的理论以来[1],经过三十多年的发展,这一理论已成为一门新兴的边缘学科,应用日益广泛。灰色系统被定义为部分信息已知、部分信息未知的系统,它处于白色及黑色之间,仅可对系统的一部分建立对应模型[2],所以灰色系统的结构不完全清楚,其中的因素也相对不完全明确,进一步,其作用机理不完全明了[3]。地面测控设备由于系统构成复杂,各部件之间并联、制约、冗余关联关系交叉存在,准确建立系统的设备状态预测模型非常困难,而采取灰色系统理论构建预测模型,以测量数据为驱动,可大大降低系统建模难度,并满足预测精度要求[4]。
1 灰色系统预测理论
灰色系统建模,是在削弱原始信息随机性、建立灰色“模块”的基础上,应用微分拟合法直接将时间序列转化为微分方程,建立的是抽象系统发展变化的动态模型,如图1 所示。运用这种模型对系统进行分析,可以反映出系统内部机制变化过程的本质,可用于预测控制。这是一种用不足信息建立信息尽可能充分的模型途径,也是充分发挥白色信息作用的途径,是用离散数据建立微分方程的一种方法,可以使抽象系统模型化、实体化[5,6]。
数据的生成方式主要有累加生成、累减生成。通常,在数列为正的情况下,数据的随机性会随累加逐步弱化,进而数据的规律性会得到提升,所以通过累加这种方式,使得数列更易于去进行逼近,从而实现以下两个目标:
①数列的随机性减小,规律性增强。
② 用于动态模型建立的中间信息更为直观。
1.1 累加生成
首先介绍以下两个概念:
①累加过程:数列X在各个时间点下的一次累加操作,记作AGO。
② 累加生成数列:通过累加过程得到的新数列。
具体地,设原始数列为:
对非负数列而言,该数列的非负摆动、无规律性均可通过累加生成转变为具有非减、递增特性的数列。
1.2 累减生成
通过数列的生成操作,也可得到一系列数据,这类数据是具有一定规律的,同时,利用该类数据也可拟合出一些特定函数。因进行了生成操作,生成的数列必然与原数列有一定差异,所以还需进一步对生成的数列进行还原。对通过累加生成的数列,可以通过累减生成数列进行数列还原。
累减生成定义为:将原始数列前后两个数据相减的操作过程,记为1-AGO。
2 灰色预测模型建立
2.1 基于GM的预测模型
建立预测模型的基本方法为:①对原始数据进行一阶累加操作;② 采取指数曲线对进行累加操作后的数据进行拟合及预测;③利用累减生成方法对数列进行还原,从而得到真实预测值。
设原始数列为X(0),一阶累加序列为X(1)。通过下述步骤可得到GM 预测模型[7,8]。
①假定原始数据序列为X(0):
式中n为样本数。
② 生成一阶累加序列为(1)X:
③对X(1)建立白化微分方程:
其中a和b为待定参数。将公式(6)微分方程离散化,可得:
④ 求解参数a和b,将式(7)移相,得到:
令k=1,2,…,n-1,则有:
则(10)式可写成:
⑤ 白化微分方程求解
令x(1)(0)=x(0)(1),则(5)式经拉氏变换有:
经整理后,可写成:
由拉氏变换对应表可得微分方程的解为:
那么,GM 模型的时间响应式为:
综上,式(17)及(18)即为GM的预测模型。
2.2 基于Verhulst的预测模型
设X(0)为原始数据序列,X(1)为X(0)的一阶累加序列(AGO),Z(1)为X(1)的紧邻均值生成序列,则称[9]
为Verhulst 模型,那么其白化过程为:
由于(20)式满足伯努利方程的构型,两边同乘以(X(1))-2,则有:
设u=(X(1))-1,则有u′=-(X(1))-2·X′(1),代入(21)式,有:
同理,由拉氏变换可以得到其微分方程的解为:
那么,Verhulst 模型的时间响应式为:
灰色系统理论自问世以来,得到了广泛的应用,特别是针对具有不确定性和缺乏数据的系统,其要求样本数据少,运算方便,可较好地反映过去的情况及将来的趋势[10]。
由上述模型可以看出,GM 模型具有较强的指数特性,更适于预测呈单调变化的数据,而Verhulst模型具有一定的非线性微分动态特性,更适于预测呈摆动变化的数据[11,12]。
与此同时,由于影响测控设备状态的因素是多元的,具有较强的随机性,如果直接利用原始数据进行处理,将致使预测精度降低,无法准确预测出测控设备状态的变化趋势,对开展装备维护带来较大难度。
3 算法改进策略
3.1 改进策略
3.1.1 非等间隔处理
传统的GM 与Verhulst 预测模型都是以等间隔序列为基础的,但在实际应用中,指标测试的时机是根据任务准备及装备维护计划而定,其指标参数具有不等间隔的特点,故首先需将不等间隔序列转化为等间隔序列,并通过相关数学处理,再恢复成非等间隔序列。
设有非等间隔原始数列:X(0)=(x(0)(t1),x(0)(t2),…,x(0)(tn)),各时段的实际间隔为:
且有Δti≠Δtj,即代表每一时段的间隔是不一致的,此时的处理方法如下:
①求解平均时间间隔Δt0
② 求各时段与平均时段的单位时段差系数μ(ti)
④ 计算等间隔点的灰数值⊗ix
可得到等间隔序列:
3.1.2 数据平滑处理
航天地面测控设备是一个复杂的机电融合系统,其故障一般为多元故障及多种故障的一个组合。所以此时的AGO 必然会具有强随机性特点。原始数据的差异性和离散性较大,故若直接采用原始数据去进行后续算法计算,必然会引发预测精度低等问题。
基于以上原因,在灰色模型中引入时间序列的一阶指数平滑公式S(t)=αY(t)+(1-α)S(t-1),α∈[0,1],对原始数据进行重新生成,即可得到一个新的数列。与原始序列相比,该序列的规律性更强,通过这种规律性,灰色预测的适用范围和精度均可得到大幅提升。
3.1.3 背景值改进
在灰色预测模型中,一般取x(1)(k)、x(1)(k-1)的均值作为背景值z(k),即z(k)=(x(1)(k)+x(1)(k-1)),其出发点是出于平均的考虑,但在实际应用中却不符合实际,在以上序列的间隔较小且渐变情况下,灰色预测的模型误差越小;反之,在序列剧烈变动情况下,预测模型的误差就会越大。
在图2 中,梯形abcd的面积即为背景值z(k)=(x(1)(k)+x(1)(k-1)),不同于实际曲线所构成的梯形面积,差值为SΔ 。随着序列变化愈发剧烈,ΔS也越大,从而会引发更大的模型误差。
故提出一种背景值的优化求解方法,如图3 所示。对[k-1,k]区域空间N等分,可近似将N个小区域面积和作为图3 中曲边梯形的面积。在N较小的情况下,实际面积大于N个小区域的面积和;在N较大的情况下,实际面积小于N个小区域的面积和。故应存在一个N值(理论值),使实际面积与N个小区域的面积和相等,在这种情况下,N个小区域的面积和可写为:
设背景值算子β=(N+1)/2N,则(N-1)/2N可记为1-β,当0≤β≤1时,则SN=βx(k+1)+(1 -β)x(k)。通过一维搜索方法,最佳的背景值算子与平均相对误差最小模型相对应。
3.2 优化处理流程
通过上述改造方法,可以对原GM(1,1)模型和Verhulst 模型进行优化,有效增强模型的适用范围,提高预测精度。其优化处理具体步骤如图4 及图5 所示。
4 测试验证
4.1 验证方法
客观规律会导致状态预测和设备实际参数存在差异,所以需要通过一些手段去考虑本文提出的预测模型是否精确合理,且结果是否可信。通过残差检验方法,对本文提出的预测模型进行检验。
设原始数据序列为X(0)=(x(0)(1),x(0)(2),…,x(0)(n)),相应的模型预测数据序列为,那么灰色模型的残差为:
其残差序列为:
其平均残差为:
4.2 仿真分析
为预测任务实施当日测控设备的健康状态,分别调用测控设备使用期间四个多月的指标参数及评估结果,以非等间隔日期原始数据为抽样对象,预测任务当天的系统健康状态。通过预测值与实际值的比对情况,验证该方法的适用性和有效性。
指标参数及评估结果见表1~表3,其对应曲线分别如图6~图8 所示。

表1 10MHz 本振输出幅度检测记录Table 1 10MHz local oscillator output amplitude detection record

表2 晶振部件评估结果统计Table 2 Statistics of evaluation results of crystal oscillator components

表3 测控设备系统状态评估结果统计Table 3 Statistics of TT&C equipment system status evaluation results
4.2.1 指标参数值的预测分析
由表4 及表5 可知,传统GM 模型的平均相对误差为-2.674 7 %,而改进方法,选取α=0.65,β=0.57,得到的平均相对误差为-1.625 8 %,模型精度高于传统GM 模型。
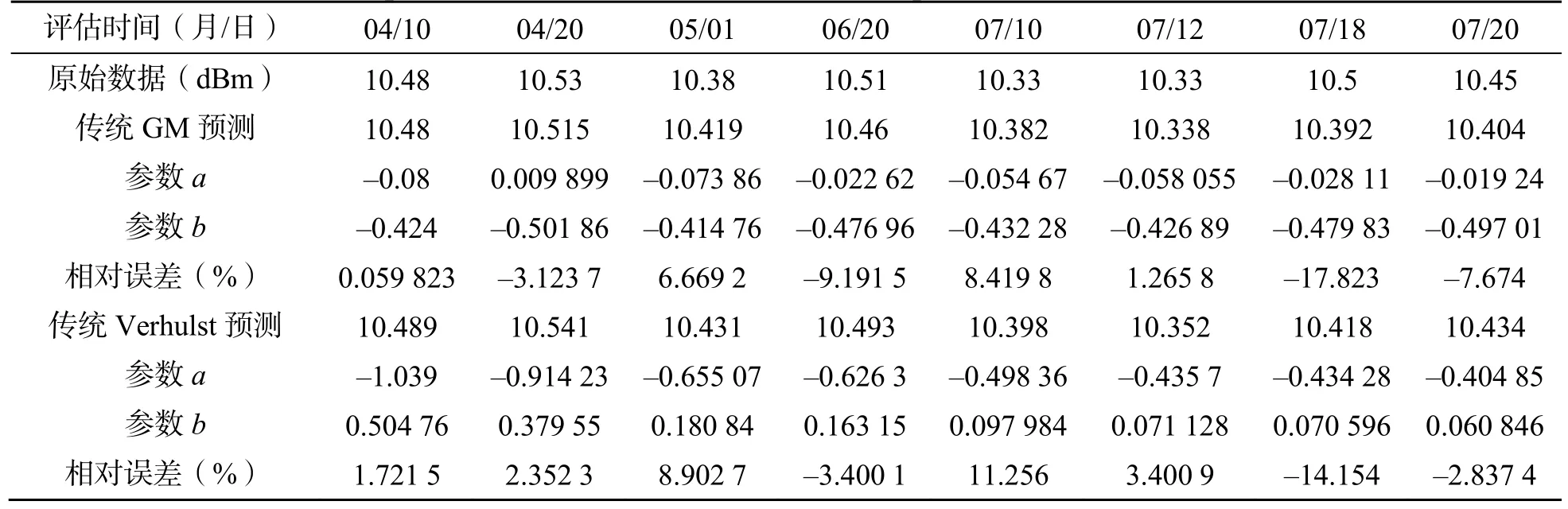
表4 10MHz 本振输出测量值与传统GM 与Verhulst 模型的预测比较Table 4 Prediction comparison of 10 MHz local oscillator output with traditional GM and Verhulst models
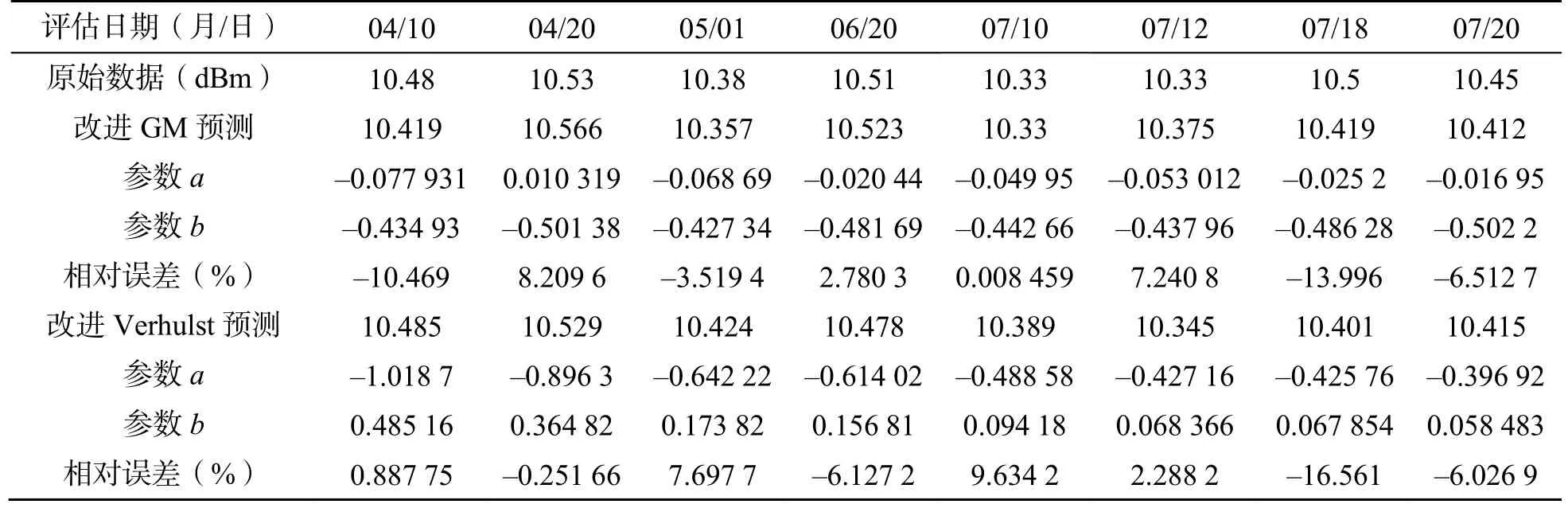
表5 10MHz 本振输出测量值与改进GM 与Verhulst 模型的预测比较Table 5 Prediction comparison of 10 MHz local oscillator output with improved GM and Verhulst models
传统Verhulst 模型的平均相对误差为0.905 19 %,而改进方法,选取β=0.51,得到的平均相对误差为-1.057 3 %。模型精度与传统Verhulst 模型相当,预测曲线如图9 所示。
4.2.2 典型部件状态评估预测分析
由表6 及表7 可知,传统GM 模型的平均相对误差为0.462 09 %,而改进方法,选取α=0.74,β=0.49,得到的平均相对误差为-0.019 667 %,模型精度高于传统GM 模型。
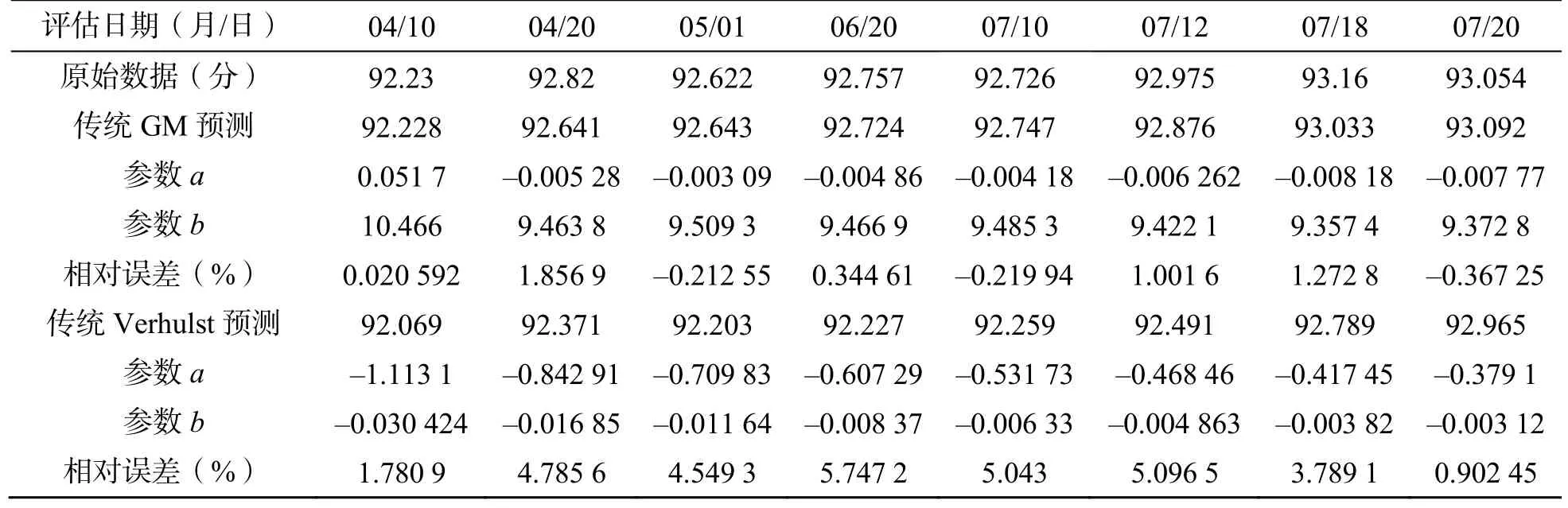
表6 晶振部件评估值与传统GM 和Verhulst 模型的预测比较Table 6 Comparison of evaluation value of crystal oscillator components with traditional GM and Verhulst models
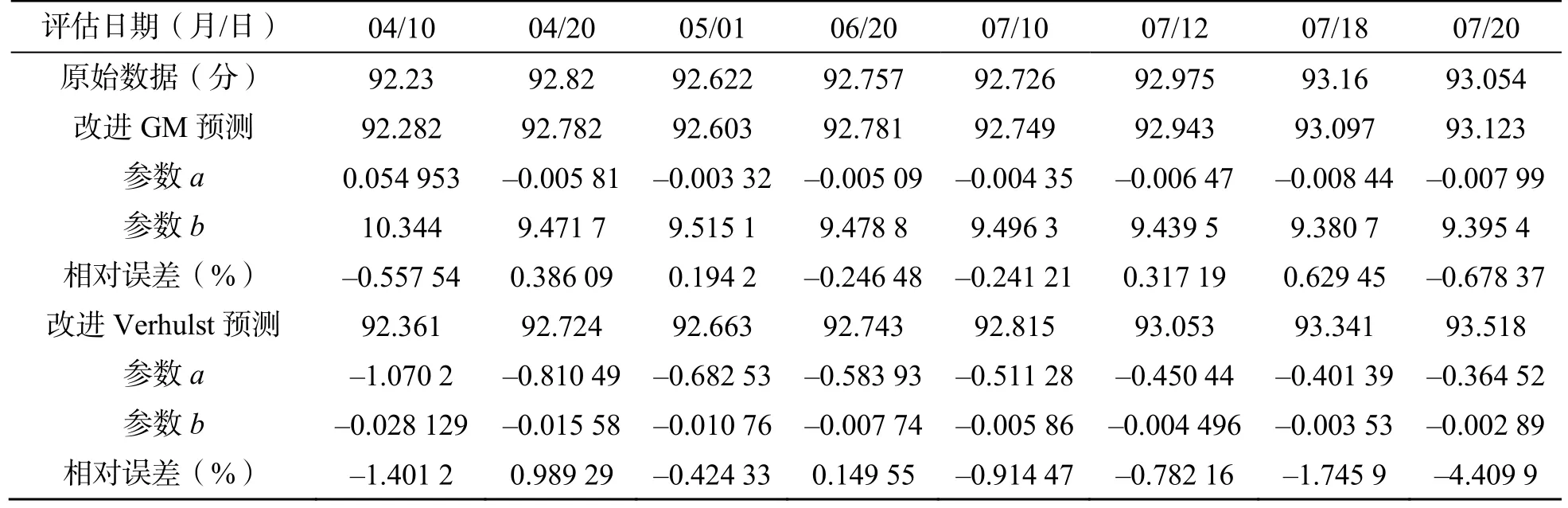
表7 晶振部件评估值与改进GM 和Verhulst 模型的预测比较Table 7 Comparison of evaluation value of crystal oscillator components and prediction of improved GM and Verhulst models
传统Verhulst 模型的平均相对误差为3.961 8 %,而改进方法,选取β=0.52,得到的平均相对误差为-1.067 4 %。模型精度高于传统Verhulst 模型。预测曲线如图10 所示。
4.2.3 测控系统状态评估预测分析
由表9 及表10 可知,传统GM 模型的平均相对误差为1.500 3 %,而改进方法,选取α=0.61,β=0.59,得到的平均相对误差为1.363 6 %,模型精度高于传统GM 模型。
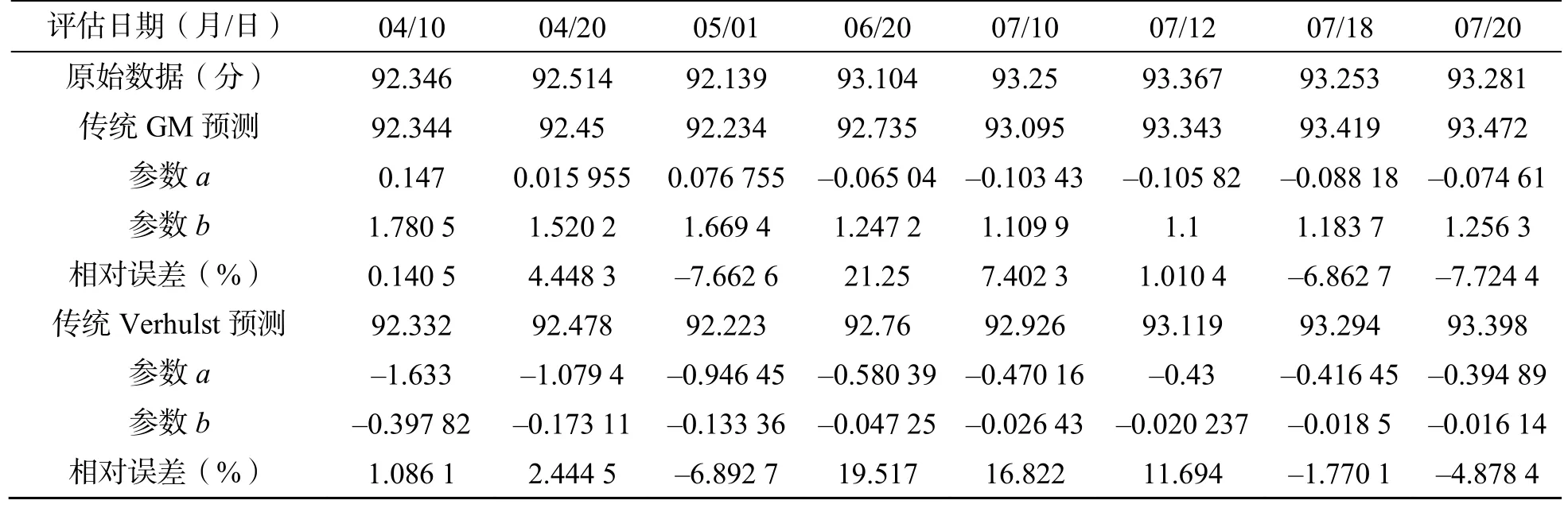
表8 测控系统状态评估值与传统GM 和Verhulst 模型的预测比较Table 8 Comparison of state evaluation value of TT&C system with traditional GM and Verhulst models
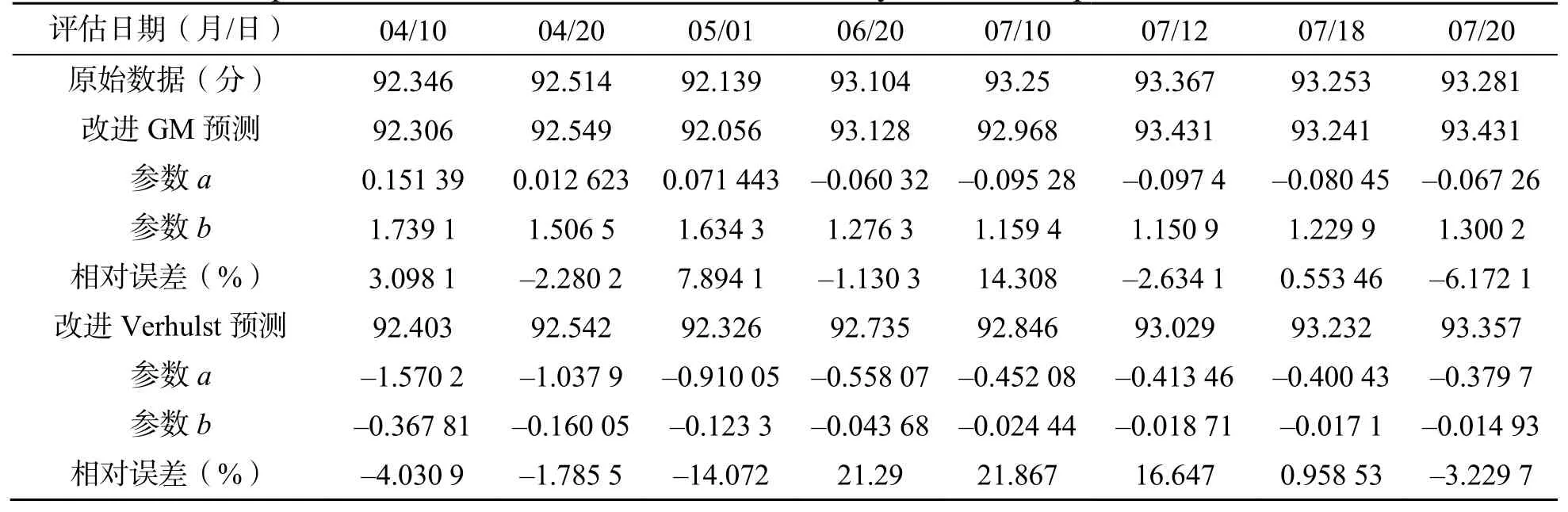
表9 测控系统状态评估值与改进GM 和Verhulst 模型的预测比较Table 9 Comparison of state evaluation value of TT&C system with improved GM and Verhulst mode
传统Verhulst 模型的平均相对误差为4.752 8 %,而改进方法,选取β=0.51,得到的平均相对误差为4.705 5 %。模型精度高于传统Verhulst 模型。预测曲线如图11 所示。
通过对上述测控设备典型参数指标的预测情况分析,可以得到如下结论:
①采用改进后的GM 模型与Verhulst 模型预测精度高于传统模型预测精度,一般能够提高2 倍以上,且适用范围更广。
② Verhulst 模型更适用于周期振荡或随机信号的预测,而GM 模型适应范围较宽,周期振荡、随机信号或者满足一定单调函数的信号均可满足预测要求。
5 结束语
本文通过对灰色系统理论进行研究,针对传统的GM 与Verhulst 模型对随机信号处理的缺陷,提出了非等间隔处理、数据平滑以及背景值修正等方法,对原状态预测模型进行了改进,将预测结果误差降低了2 倍以上,有效地提高了地面测控设备状态预测精度,为后续工程化应用及开展视情维修提供了决策支持。

