钢混组合梁桥车桥耦合竖向振动分析

李喜梅， 徐 伟， 母渤海

(1. 兰州理工大学 a. 西部土木工程防灾减灾教育部工程研究中心， b. 防震减灾研究所， 兰州 730050； 2. 中国市政工程西北设计研究院有限公司， 兰州 730050)

目前，桥梁车桥耦合振动有关的研究主要采用数值分析的方法[4].现有的数值分析方法主要有整体法和分离法两种，经对比研究，分离法适用范围更广，求解速度更快[5].施颖等[6]采用ANSYS软件通过几次迭代计算实现车桥耦合振动的求解；蒋培文等[7]基于ANSYS分别建立桥梁模型和车辆模型，并将其看作两个独立单元，避免了车桥系统振动方程的推导；刘世忠等[8]提出基于ANSYS利用约束方程实现车轮与桥面接触点位移协调的车桥耦合振动响应的数值分析方法，该方法不需要迭代计算，能极大提高分析效率.综上可知，国内许多学者应用ANSYS软件尝试用不同方法分析车桥耦合振动，并且在特定条件下使求解具有适用性.

1 车桥耦合振动分析模型

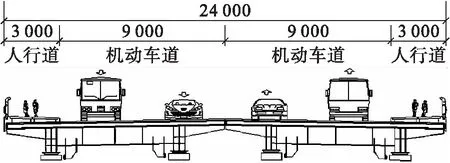
图1 桥面布置示意图

图2 桥梁有限元模型

1.2 车辆空间模型

建立的车辆三维模型除了考虑六个车轮的竖向位移Zs1～Zs6、车体的竖向位移Zv，还考虑了车体侧倾角位移φv和车体俯仰角位移θv共9个自由度.其中：m1～m6为六个车轮的质量；mv为车体的质量；Cu1～Cu6、Ku1～Ku6分别为车悬架阻尼和刚度；Cd1～Cd6、Kd1～Kd6分别为轮胎的阻尼和刚度.车辆模型如图3所示.

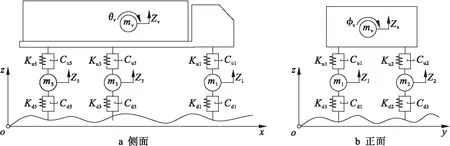
图3 车辆模型

2 桥面不平顺模拟

对于路面不平顺的描述，我国主要采用GB/T7031-2005标准[9]建议的功率谱密度进行.假设桥面不平顺和一般路面不平顺是相同的，依据GB/T7031-2005标准给出的路面功率谱密度函数拟合公式为

(1)

式中：Gd(n0)为路面平度系数；n为空间频率；n0为参考空间频率，取n0=0.1 m-1；w为频率指数，一般取w=2.

采用三角级数法生成路面不平度函数，即

(2)

式中：x为桥面纵向坐标值；N为总采样点数；nk为空间频率，nk=nd+(k-1/2)Δn，k=1，2，…，N；Δn为频率间隔带宽，Δn=(nu-nd)/N；nu、nd为有效空间频率上、下限；φk为随机相位角.

本文取前三级路面模拟桥面不平顺，基于MATLAB软件采用上述方法求得A级、B级和C级桥面不平顺样本函数，如图4所示.

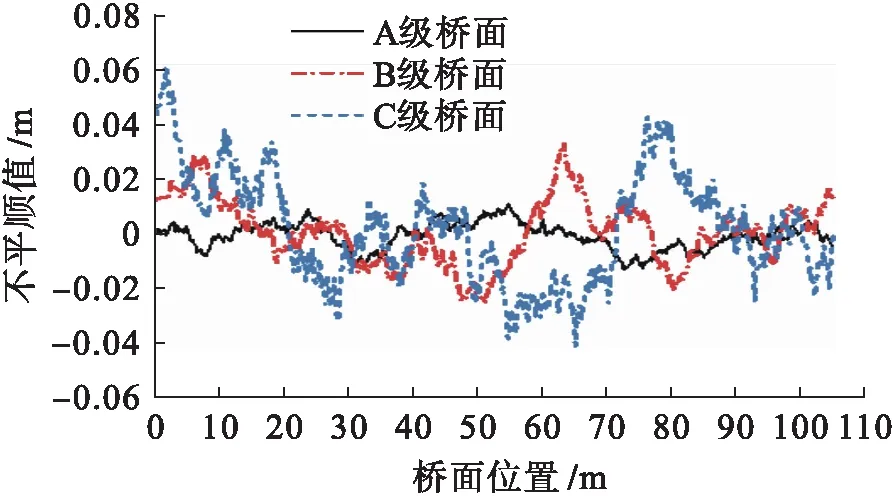
图4 桥面不平顺样本函数

3 车桥系统耦合振动分析方法

(3)

(4)

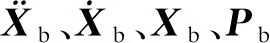
为实现车辆、桥梁系统各自振动方程的求解，需考虑车轮与桥面接触位置的位移协调和相互作用力平衡条件.假设车辆行驶过程中车轮不脱离桥面，并考虑桥面不平顺的影响，则车轮与桥面竖向位移的相对值可表示为

Δ=Zs-r-Zb

(5)

式中：Zs为车轮竖向位移；r为桥面不平顺值；Zb为车轮处的桥面位移.由牛顿第三定律可知，车轮与桥面接触位置作用力与反作用力大小相等，方向相反，可表示为

(6)

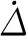
为保证振动微分方程的求解精度，实时对计算结果的收敛性进行判断，本文选用位移收敛指标控制计算过程的收敛性，即

(7)

式中：Zt和Zt+1分别为t时刻和t+1时刻车桥接触位置的位移值；ε为位移控制参数，王贵春等[10]将ε取值设为0.01.

最后，基于ANSYS软件编写求解振动微分方程的APDL命令流，并将MATLAB软件生成的桥面不平顺值形成数组，以宏文件形式载入ANSYS中，满足位移协调和力的平衡条件，由此实现车辆和桥梁振动微分方程的联合迭代求解.

4 数值模拟及行人舒适度评价

Sperling平稳性指标[11]是常用的振动舒适度评价标准，本文选择该指标作为舒适度评价指标，其表达式为

(8)

式中：Wz为单一频率下的平稳性指标；z为振幅；f为振动频率；F(f)为频率修正系数，数值如表1所示.Sperling平稳性指标评定标准如表2所示.

表1 频率修正系数

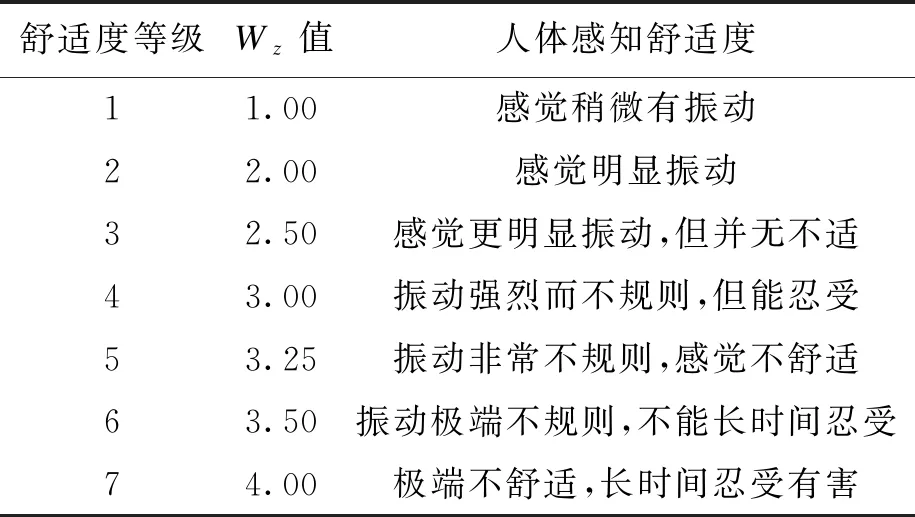
表2 Sperling指标评定标准

4.1 行车速度的影响

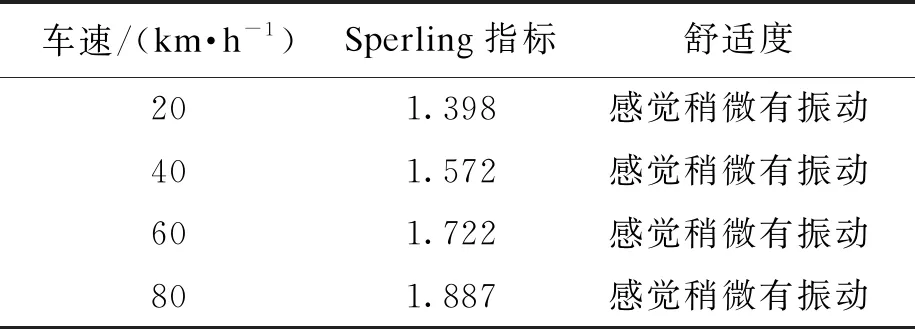
表3 不同车速时的行人舒适度评价

4.2 车辆载重的影响

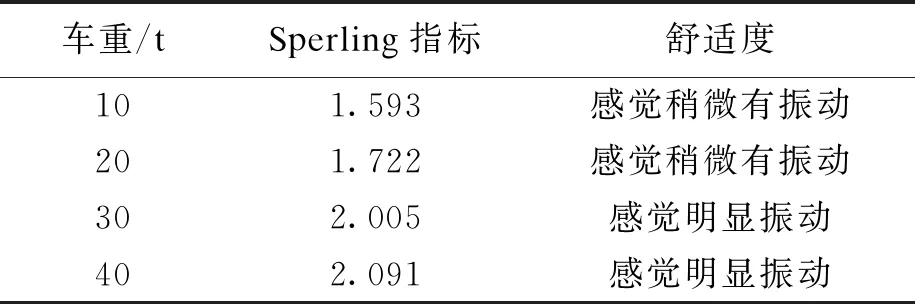
表4 不同车重时的行人舒适度评价

由图6可知，在上述条件下，随着车重的增加，该桥边跨跨中竖向位移明显增大，车重40 t时边跨跨中竖向位移幅值(6.544 mm)是车重10 t时对应位移幅值(1.619 mm)的4.042倍.随着车重的增加，边跨跨中竖向位移曲线波动呈加剧趋势，说明车重对该桥型的车桥耦合振动影响较大.

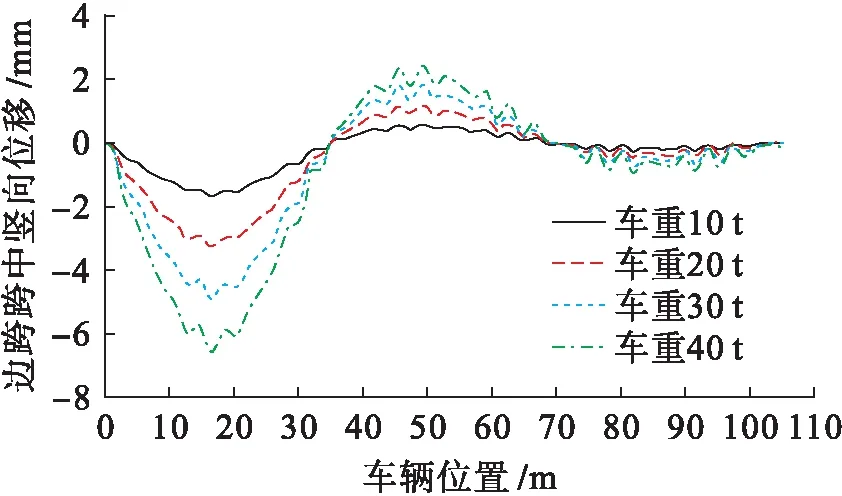
图6 不同车重时桥梁边跨跨中竖向位移

4.3 桥面不平顺的影响

表5 不同桥面不平顺等级时的行人舒适度评价

由图7可知，重20 t的汽车以60 km/h的速度通过不同平整状况的桥面时，随着桥面状况的恶化，该桥边跨跨中竖向位移均明显增大，C级桥面下桥梁边跨跨中竖向位移幅值(4.115 mm)是A级桥面对应位移幅值(3.275 mm)的1.256倍.随着桥面状况的恶化，竖向位移曲线波动显著加剧，说明桥面不平顺是该桥型车桥耦合振动最重要的影响因素.

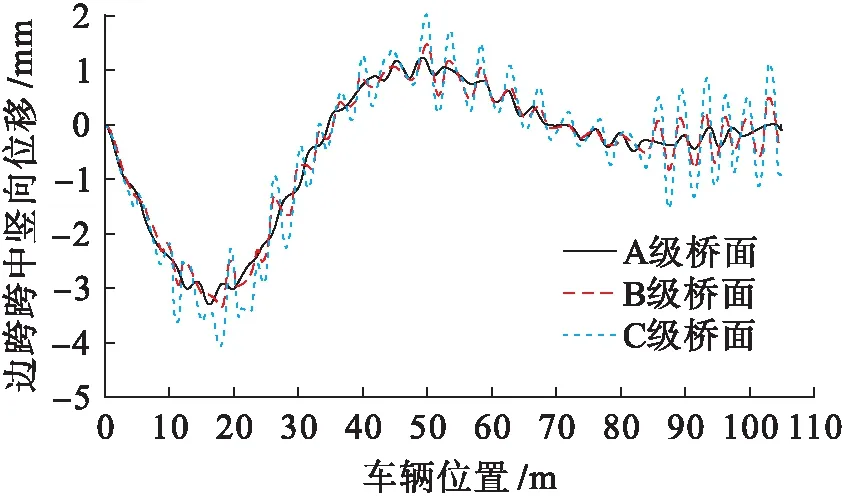
图7 不同桥面不平顺等级时桥梁边跨跨中竖向位移

5 重载车辆过桥冲击系数计算

近年来，公路交通运输系统面临着繁重的交通压力，重型车辆过桥时的安全问题不容忽视.冲击系数是车辆对桥梁冲击效应的直观反映，同时也是对桥梁状况进行评估的重要参数，因此有必要计算考虑车桥耦合振动作用的重型车辆对桥梁的冲击系数.

考虑到车辆自振特性、行车速度、桥面不平顺度、车桥耦合作用等因素的不确定性，计算冲击系数时可选择考虑动力效应的公式.按我国《公路桥梁荷载试验规程》(JTG/T J21-01-2015)[12]采用动挠度计算冲击系数，冲击系数可表示为

(9)

式中：Ydmax为最大动挠度幅值；Yjmax为波形振幅中心轨迹的顶点值.

为了考察所算得的冲击系数与规范设计值之间的差异性，先根据我国《公路桥涵设计通用规范》(JTG D60-2015)[13]采用桥梁基频(测得基频为2.71 Hz)计算该桥冲击系数限值为0.16，然后用动挠度算得的冲击系数与之作对比分析.

40 t重型车在该桥A级、B级、C级桥面上以20、40、60、80 km/h的速度行驶时，桥梁第一跨跨中挠度冲击系数变化如图8和表6所示.

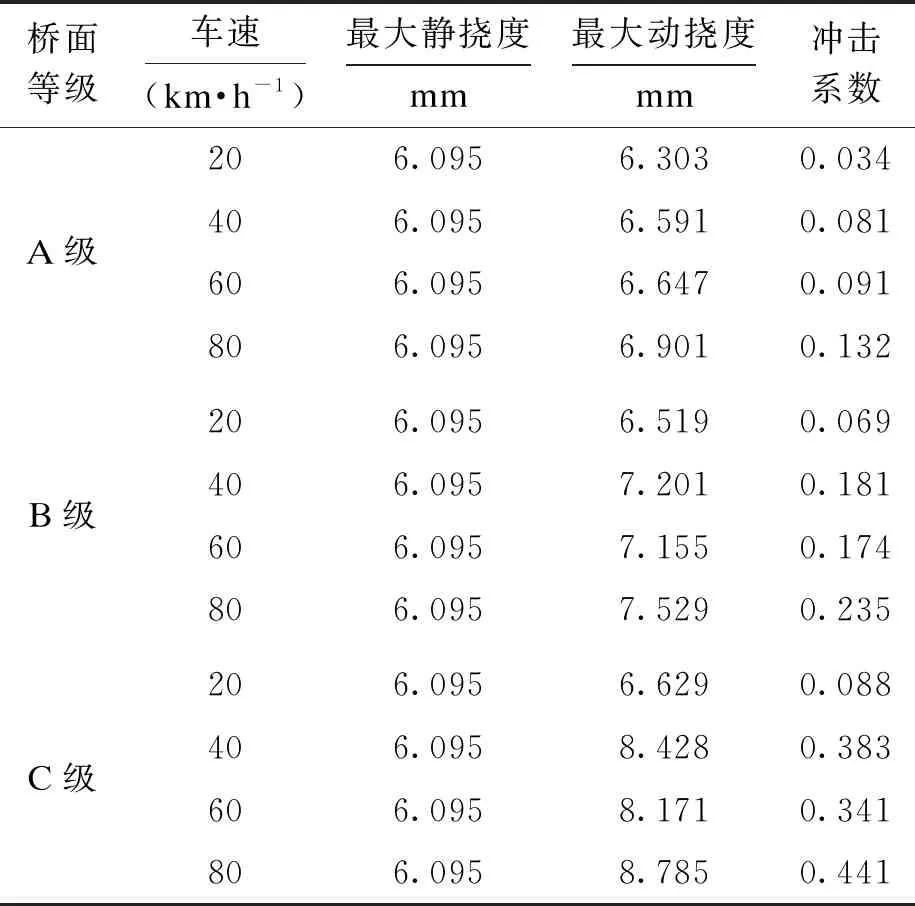
表6 不同桥面不平顺等级和车速下第一跨跨中挠度及冲击系数

6 结 论

5) 桥面等级为A级时，随着车速增加，冲击系数不断增大，但均未超过通用桥规限值.桥面等级为B级时，算得的冲击系数与通用桥规限值吻合良好.桥面等级为C级时，在一定车速下冲击系数远大于通用桥规限值.因此，以动挠度算得的冲击系数和通用桥规中以桥梁基频为参数算得的冲击系数有较大差异，其中桥面不平顺是最重要的影响因素.