基于球孔扩张理论的静压桩桩端阻力解析解

李雨浓， 曹锦楼， 王立伟， 曹海莹

(燕山大学 a. 河北省土木工程绿色建造与智能运维重点实验室， b. 建筑工程与力学学院， 河北 秦皇岛 066004)

静压桩凭借无振动、污染小、施工速度快以及桩身质量可靠等优点，在软土地区城市建设中已得到广泛应用.在实际工程中，合理地估算沉桩阻力对于桩型的设计、承载力的判断和压装机的选择等有重要的意义.

桩端阻力的大小主要是由土体的性质决定的.因此，本文针对静压桩在饱和黏土中的沉桩情况，对其桩端阻力进行分析.将静力贯入过程中的桩端作用视作半无限土体内的球孔扩张，材料的破坏服从考虑中主应力的拓展Lade-Duncan屈服准则，通过理论推导建立了饱和黏土中球孔扩张的弹塑性解析解答.桩体对土体的挤压作用主要发生在桩端，桩体贯入对土体影响的大小很大程度上取决于桩端扩张应力的大小.在刘俊伟等[7]研究的基础上，根据极限扩孔压力解答给出静压桩桩端阻力极限值的表达式.本文计算方法对于桩端承载力的判断具有一定的参考价值.

1 理论分析模型

1.1 拓展Lade-Duncan屈服准则

Lade-Duncan模型最初是由是莱特(Lade)和邓肯(Duncan)在砂土真三轴试验基础上建立起来的适用于无黏性土应力变形分析的弹塑性理想本构模型，后经莱特的修正与完善，近年来广泛应用于工程实践中.Lade-Duncan模型的屈服准则不同于其他强度准则，其应力不变量的表达式为

(1)

式中：Kf为强度参数；I1、I3分别为无黏性土的第一、第三次不变量，即

(2)

其中，σ1、σ2、σ3为无黏性土的三向应力.

Lade-Duncan屈服准则虽然能有效地反映中主应力的影响，但只适用于无黏性土.因此，基于Lade-Duncan破坏准则及平面应变条件，推导出了无黏性材料的平面应变破坏公式，通过引入粘结应力σ0，将其推广到c-φ材料.

平面应变条件下黏性土破坏准则可表示为

τ=cps+σtanφps

(3)

式中：cps为平面应变条件下的粘聚力；σ为黏土的正应力；φps为平面应变条件下土体的内摩擦角.

因此，基于Lade-Duncan准则的平面应变条件下黏性土的破坏准则为

σ1-ησ3-(η-1)σ0=0

(4)

其中，

(5)

(6)

σ0=ccotφ

(7)

式中：c为土体粘聚力；φ为内摩擦角.

1.2 力学模型

静压桩桩端对土体会产生挤压和扩张，因此，桩端作用可通过半无限土体内的球孔扩张来模拟.为建立静压沉桩过程的力学模型，现作出如下基本假定：

1) 土体是均匀、各向同性的理想弹塑性材料；

2) 土体服从拓展Lade-Duncan屈服准则；

3) 土体饱和、不可压缩，将球孔扩张看作不排水过程；

4) 不考虑桩体自重的影响，球孔最终扩孔半径等于桩体的半径.

图1为半无限土体中球孔扩张的力学模型.球孔在内压力p的作用下进行扩张，当p较小时，球孔周围土体处于弹性状态.随着p的增大，围绕球形孔的球形区域将由弹性状态进入塑性状态，塑性区域随着内压力p的增大而不断扩大.球孔的初始半径为R0，最终扩孔半径为Ru，相应的极限扩孔压力为pu，r为扩张后土体单元距孔心的距离，塑性区最大半径为Rp，up为塑性区外侧边界径向位移.塑性区半径Rp以外区域的土体仍保持弹性状态，弹塑性交界处径向应力为σp.

2 球孔扩张弹塑性解答

2.1 基本方程

球孔扩张属于球对称问题，在极坐标下，平衡微分方程为

(8)

式中，σr、σθ分别为径向应力和环向应力.

在弹性区采用小变形理论，几何方程为

(9)

(10)

式中：εr、εθ分别为径向应变和环向应变；ur为径向位移.

根据胡克定律，弹性本构方程为

(11)

(12)

式中：E为弹性模量；v为泊松比.

2.2 弹性区分析

运用弹性理论的应力解法，结合边界条件(r=R0，σr=p)可知弹性区的应力及位移解答为

(13)

(14)

(15)

2.3 塑性区分析

将拓展Lade-Duncan屈服准则(4)代入平衡微分方程(8)可得

(16)

对式(16)进行积分后得

(17)

式中：α=1-1/η；D为任意常数.

根据边界条件(r=Ru，σr=pu)，可得塑性区应力场解答为

(18)

(19)

球孔扩张过程可以看作不排水过程，球孔周围的土体体积应变为零[13].忽略塑性材料在弹性阶段的体积变化，扩孔过程中排开土体的体积等于塑性区体积变化量，则在弹塑性交界面处有

(20)

对式(20)进行展开，并略去up和R0的高次项(因为塑性区外侧边界径向位移up和初始扩孔半径R0都较小)，可得

(21)

由式(15)和边界条件(r=Rp，σr=σp)可得

(22)

根据式(13)、(14)可知，在弹塑性交界面处有

σr=-2σθ=σp

(23)

将式(23)代入式(4)可得

(24)

由式(22)、(24)可得

(25)

合并式(21)、(25)消去up可得

(26)

由式(26)可求出塑性区半径的解答为

(27)

式中，G为土体的剪切模量，G=E/[2(1+v)].

由式(18)可知，在弹塑性交界面处径向应力表达式为

(28)

联立式(24)和(28)可得

(29)

将式(27)代入式(29)中可得极限扩孔压力的表达式为

(30)

由式(21)和(27)可知塑性区外侧边界径向位移的表达式为

(31)

2.4 极限桩端阻力的确定

桩端阻力是由桩端穿透土层时受到土体抗力引起的，其最大值可利用极限扩孔压力与桩端作用面积的乘积得到.由图1可知，桩端与土的模拟接触面为半个球面，可得静压桩贯入土中的桩端阻力极限值为

(32)

将式(30)代入式(32)可得

(33)

3 模型试验验证与分析

3.1 试验装置

试验所采用的模型箱尺寸为100 cm×60 cm×100 cm(长×宽×高).模型桩分别采用直径D为2、3和5 cm的平底型闭口空心有机玻璃管桩，桩身长100 cm，压桩深度L为60 cm.在开口管桩内腔的底部以及距桩底20、40和60 cm的高度处粘土应变片，根据所测量的应变值可计算出各断面的应力.图2为试验压桩装置.加载系统由液压式压力机改装而成，压力传感器放置于反力梁与模型桩帽之间.图3为数据采集系统，通过量程为2×103kg的压力传感器施加荷载同时自动读取桩顶荷载值，静态应变仪采集数据并进行记录，桩顶沉降量通过百分表进行读测[14].

图2 试验压桩装置

图3 数据采集系统

3.2 试验土样

土样选用50目高岭黏土，根据饱和含水率配制水量，经搅拌均匀，倒入模型箱中，并充分捣实土体，当土体加到一定高度后再铺上土工织布，在上面压一些砝码，让其在一定的压力下固结60 d.模型土样基本参数如下：土体粘聚力c=29.98 kPa，内摩擦角φ=19°，弹性模量E=2.3×103kPa，泊松比v=0.4.

3.3 试验结果对比分析

为验证本文推导方法的可靠性，分别作出桩径D为2、3和5 cm模型桩沉桩端阻力的实测值与理论极限值的对比图，如图4～6所示.

图4 2 cm桩径端阻力

由图4～6可知，不同桩径模型桩的桩端阻力实测值与压桩深度的发展趋势基本相同.在沉桩初期，桩端阻力增长较快；到沉桩后期，桩端阻力的增长速率放缓并趋于稳定；沉桩终止时，桩端阻力的实测值均小于理论极限值.

图4中，静压沉桩到60 cm深度处时(L/D=30)，测得沉桩阻力为101.02 N，通过本文理论方法计算所得的桩端阻力极限值为107.4 N，实测值与理论极限值非常接近，只差6.3%.由图5可以看出，压桩至60 cm深度时(L/D=20)，桩端阻力实测值为197.04 N，而理论极限值为241.7 N，极限值比最大实测值增长了22.7%.图6中，沉桩终止时(L/D=12)的桩端阻力实测值为310.07 N，极限端阻力计算值为671.6 N，远远大于沉桩终止时的实测值，增长幅度高达116.6%.由式(32)可知，桩端阻力极限值是随着桩体半径呈二次幂增长的，但根据模型试验的实际测量结果可知，随着桩径的增大，同一土层中的沉桩极限端阻力并没有随着桩径的变大出现理论性的大幅度增长.因此，长桩在沉桩终止时的最大桩端阻力更贴近理论极限值.

图5 3 cm桩径端阻力

图6 5 cm桩径端阻力

3.4 参数分析

粘聚力和内摩擦角作为黏土的重要参数指标，对桩端阻力也存在相应的影响.图7为不同粘聚力下极限端阻力与半径关系曲线.从图7中可以看出，随着粘聚力的增大，极限桩端阻力增大，但增长幅度变小.图8为不同内摩擦角下极限端阻力与半径关系曲线.从图8中可以看出，土体内摩擦角越大，对应的极限桩端阻力也越大.随着半径的增长，不同内摩擦角之间极限端阻力的差距越来越明显.

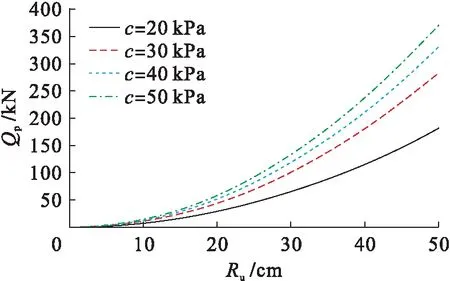
图7 不同粘聚力下极限端阻力与半径关系曲线

图8 不同内摩擦角下极限端阻力与半径关系曲线

4 结 论

本文通过分析得出以下结论：

1) 本文通过模型试验来模拟静压桩的沉桩过程，结果表明，桩端阻力随着压桩深度先是快速增长，而后渐渐变缓并趋于平稳.桩径越大，所受的桩端阻力也越大.

2) 极限桩端阻力的理论计算值随着桩体半径呈二次曲线增长，并且随着土体粘聚力和内摩擦角的增大而变大.

3) 本文理论方法能近似计算极限桩端阻力，经对比分析可知，该计算模式对于长桩在饱和黏土中沉桩桩端承载力的估算是可行的，具有一定的理论参考价值.