铁路实体墩墩顶温差位移及规范适应性研究

王雨权

(中国铁路设计集团有限公司，天津 300308)

温度应力导致混凝土桥梁破坏的事例屡见不鲜，如加拿大朗梅尔大桥，美国Chempogny箱形桥[1]，因此，温度效应引起科学和工程界的广泛关注。我国铁道部科学研究院西南研究所自20世纪70年代开始就对混凝土桥梁的温度场和温度应力变形问题进行过一系列的研究。

TB 10002.1—2005《铁路桥涵设计基本规范》(以下简称“《2005年桥规》”)[2]修订计算桥墩横向位移时考虑了日照温差的影响，TB 10002—2017《铁路桥涵设计规范》(以下简称“《2017年桥规》”)[3]沿用了《2005年桥规》规定[4]。目前规范需要验算0.4倍风荷载与0.5倍桥墩温差的工况组合，《铁路工程设计技术手册：桥梁墩台》[5]提供了圆形和圆端型空心墩的日照温差的墩顶位移计算公式，但现行规范和手册均未对实体桥墩在日照温度场条件下的横向墩顶位移计算公式进行描述，使得设计人员在设计实体桥墩时，很难执行规范要求。

因此，本文在查阅相关资料的基础上，将上述规范及手册缺失的内容补上，从温度场及实体桥墩墩顶位移两个方面进行论述。

1 温度场

1.1 温度荷载分类

混凝土结构的温度随环境而变，表面和内部也不同。因自然环境变化所产生的温度荷载，一般可分为3类：①结构年均匀温度变化荷载；②日照温度荷载；③骤然降温温度荷载。

结构年均匀温度变化荷载，上部结构发生伸缩变形，设计中早已考虑；骤然降温温度荷载变化较日照温度荷载缓慢、作用时间长；日照温度荷载则比较复杂，与太阳的辐射强度、风速和气候有关。并且桥梁构件的构造对温度分布有明显的影响。对于混凝土箱梁，沿顶板表面温度分布比较均匀，沿腹板表面的温度分布则随时间而变。混凝土桥墩结构的垂直表面的温度分布，与表面的朝向、太阳方位角有关。

因此，要进行日照温度荷载效应分析，必须先确定结构内的温度场。

1.2 温度场的数学表达

计算温度效应，一般有3种方法：一是热传导微分方程求解[6-8]；二是数值仿真[9-14]；三是半理论半经验公式[15-17]。在桥梁工程设计中，一般采用半理论半经验公式，以某一特定时刻最大温差分布作为结构设计的温度效应控制参数。

国际上，英国D.A.Stephenson用指数表达式T(x)=A0e-cxx来表示板厚温度分布，cx取试验参数。新西兰M.J.N.Priestlay在对高架桥箱梁进行模型试验后，也得出了同样的分布规律。

20世纪70年代中期，铁道部科学研究院西南研究所刘兴法，根据混凝土箱形桥墩的实测资料分析结果，提出了分析壁厚方向的温度分布表达式

T(x)=T0e-cxx

(1)

式中，T0为墩壁内外表面的温差；cx≈10。

国内外已有实测资料分析的结果也表明；沿箱梁高、梁宽方向的温度分布一般也可按下式计算

(2)

式中，T0y、T0x分别为沿梁高、梁宽方向的温差；y、x为计算点至受热表面的距离；cy、cx为指数系数，随结构形式、部位、计算时刻等因素而异。

由于指数型温度场[18-19]的计算较为复杂，为便于计算，在工程设计中，有时会采用等效的线性温度场。

2 温度位移计算

墩高较高时，因日照和气温变化作用而产生的温度应力和位移，往往成为设计的控制因素[20]，鉴于缺少实体桥墩的墩顶温差位移计算公式，下面对此展开分析。

2.1 等效线性温差

首先分析桥墩在线性温差下的墩顶位移，如图1所示。墩高为H、纵向厚度为B、横向宽为D的等截面桥墩，在日照温度作用下，墩身向阳侧温度由T0上升到T2，墩身遮荫侧温度由T0上升到T1，假设墩身温度从T2到T1线性变化，图1中y表示桥墩截面平面方向坐标，z表示桥墩高度方向坐标。

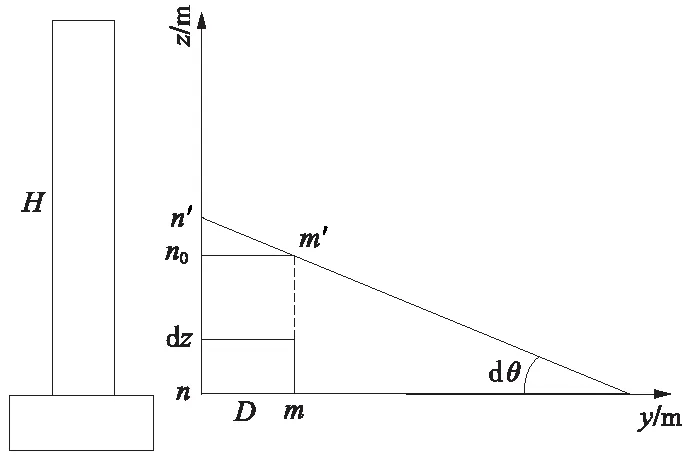
图1 线性温差下墩顶位移示意

忽略梁体对墩顶的约束作用，偏于安全设计考虑，墩顶按自由端处理，从墩身任意位置取一微元体dz进行分析。

向阳侧温度T0上升到T2时，高度dz将增至dz+α(T2-T0)dz，遮荫侧温度T0上升到T1时，高度dz将增至dz+α(T1-T0)dz，微元将形成一个角度dθ。

由于温度按线性变化，由图1可知

n0n′=Ddθ

(3)

n0n′=nn′-mm′=dz+α(T2-T0)dz-

[dz+α(T1-T0)dz]=α(T2-T1)dz

(4)

联立式(3)、式(4)可得

(5)

设由于向阳侧与遮荫侧微元伸长量不同，产生横向位移Δy，该值与角度dθ的关系有

(6)

联立式(5)、式(6)可得

(7)

微分方程(7)的边界条件为

(8)

由此可得到

(9)

因此，墩顶的横向位移为

(10)

当D随墩身的高度而变化时，可将墩身分节求和计算。

(11)

式中，α为线膨胀系数；H为墩的高度；ΔT为等效线性温差值；Di为第i节墩身横桥向宽度；n为计算分节数；zi为第i节节中心至墩顶距离；Δzi为计算分节节长。

2.2 非线性温差

日照辐射温度场为指数型时，温度场表述为

T(y)=T0e-ay

(12)

式中，T0为墩身向阳侧与遮荫侧表面的温差，a为指数系数。

桥墩截面中温差产生的自由应变为

εT(y)=αT(y)

(13)

式中，α为材料的线膨胀系数。

由于截面的平截面假定，设其实际应变为

ε(y)=ε0+ρy

(14)

式中，ε0为墩受辐射一侧的应变；ρ为截面处微段的曲率。

自由应变与实际应变之差即为自约束应变

εσ(y)=εT(y)-ε(y)=αT(y)-(εo+ρy)

(15)

则自约束应力

σε(y)=Eεσ(y)=E[αT(y)-(εo+ρy)]

(16)

式中，E为混凝土弹性横量。

因截面自约束应力处于自平衡状态，故有

∑N=0， ∑M=0

(17)

将式(16)代入式(17)

(18)

求解式(18)可得

(19)

当墩身为等截面时，由截面的弯曲曲率方程的二次积分便可得出墩顶的横向位移Δs。

(20)

当墩身截面随高度而变化时，可分节求和

(21)

式中，T0为非线性温差值，其余参数同上。

2.3 等效线性温差参数计算

从一些实体墩的实测温度场分布来看，其结构内的温差按指数形式呈非线性分布，但为简化计算，有时需简化成线性温差，此时就需要解决等效线性温度场参数ΔT的取值问题。

将式(10)和式(20)等效，联立求解可得

(22)

根据国内外实测资料，一般有：a=6～12，T0=20 ℃，桥墩横向宽度D=4～7 m，将这些参数按计算得出ΔT最大的原则代入式(22)可得：ΔTmax≈5 ℃。

德国规范就是按线性温差5 ℃考虑的，与本文分析基本一致。

因此，在实际使用中，可以按如下原则计算实体墩的温差位移。

(1)有实体墩日照温度场的，可按实际的非线性温度场分布，采用式(20)和式(21)进行计算。

(2)对于缺少温度场的，可按5 ℃线性温差分布，采用式(10)和式(11)进行计算。

3 规范适应性研究

在桥墩通用图中，一般只给出桥墩墩顶弹性水平位移，下面以通用图“叁桥4023”的相关尺寸为例，说明计入温度效应后的规范适应性问题。

分别选取直线和曲线两套系列尺寸进行计算，计算中，对于圆端型桥墩的曲线部分，可以通过面积相等换算成直线长度，公式如下

(23)

式中，D′为单侧曲线的换算宽度；r为圆端形墩半径。

直线段和曲线段桥墩在按照规范规定考虑温差效应后，其对应的折算角计算值分别如表1、表2所示。

表1 叁桥4023实体圆端形墩(直线)温差5℃

表2 叁桥4023实体圆端形墩(曲线)温差5 ℃

从表1、表2可以看出，通用图在考虑0.5倍温差效应后，其墩顶位移满足要求。

进一步分析发现，同一跨度随着墩高的增加，温度变形作用逐步增大。对于直线桥墩，墩高18～30 m的温差效应引起的水平折角达到0.12‰～0.18‰；对于曲线桥墩，水平折角达到0.10‰～0.18‰。

根据《2017年桥规》5.4.5条规定，跨度<40 m的梁端水平折角不应<1.5‰，此处2个算例的梁跨均为32 m梁，其允许值采用1.5‰。可以看出，温度引起的水平折角占规范规定允许值的角度1.5‰占比约为12%，按照规范规定折半考虑后，对于试算的桥墩通用图，温度引起的墩顶位移比较小，通用图中只给出桥墩墩顶弹性水平位移，基本不影响设计。

4 结论

本文系统梳理了铁路温度场，并针对规范中实体桥墩温差位移计算公式缺失的情况，给出了在等效线性温度场和非线性温度场情况下，墩顶温差位移计算公式的详细推导过程。结论如下。

(1)从理论推导的角度，详细给出了用于实体桥墩温差计算的墩顶位移计算公式，弥补了现行2017版桥规计算公式的空白。

(2)分别从线性温度场和非线性温度场出发，推导出两套计算公式，并基于位移等效原则，结合常规桥墩截面尺寸、温度取值，得到等效线性温差为5 ℃，与德国规范一致。

(3)针对设计中已知温度场的桥墩，可利用非线性温度场计算公式计算温差墩顶位移；对于设计中缺少温度场的，可按5 ℃等效线性温差计算温差墩顶位移。

(4)温差墩顶位移随着墩高逐步增加，占比约为允许折角的12%，规范规定折半考虑后，对于实体桥墩设计，通用图中只给出桥墩墩顶的弹性水平位移，基本不影响设计。