带有拒绝、恶化效应和安装时间的单机排序

赵玉芳, 梁 媛

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)

0 引 言

在传统的排序问题中,所有的工件都需要加工。然而,在实际问题中,机器的加工能力有限,若拒绝部分工件反而可能获得更大的利润。因而决策者需要将工件集进行划分,一般分为接受工件集与拒绝工件集。接受工件在机器上加工,拒绝工件外包处理或直接搁置,外包需要支付代加工费,搁置工件也有仓库费用,如此产生拒绝惩罚。恶化效应在现实生活中的很多地方都有体现,比如在钢铁的锻造生产过程中[1]。安装时间也称为调整时间,即机器在处理不同的工件时都有一个调整时间,在实际生产中也是普遍存在的。

对于拒绝问题,Bartal等[2]研究了多处理机排序问题,目标函数是接受工件的最大完工时间与拒绝工件的总拒绝惩罚之和,并给出了近似算法。Gerstl和Mosheiov[3]研究了带有拒绝、工期依赖于工件位置的单机排序问题,目标函数是最大延误或总延误与拒绝惩罚之和,证明了上述2个问题都是NP难的,并给出了伪多项式动态规划算法和启发式算法。Shabtay等[4]综述了带有拒绝的排序问题。Agnetis和Mosheiov[5]研究了带有拒绝、加工时间依赖位置但不依赖于机器的流水作业问题,目标函数是最大完工时间,并证明了问题是多项式时间可解的。工件的恶化效应是由Browne和Yechiali[6]提出的,他们认为工件的加工时间是开始时间的函数,并在假设加工时间为线性恶化模型时,讨论了极小化流水作业问题。Wang和Liang[7]研究了带有成组技术与简单线性恶化效应的单机资源分配问题。在2种特殊情况下,给出多项式时间算法;在一般情况下,由于极小化最大完工时间问题受到有限可用资源的约束,因而提出了一个启发式算法与分枝定界算法。Zhao和Hsu[8]考虑了带有恶化效应、工期指派和资源分配的极小化加权误工任务数的单机排序问题,提出了一个伪多项式时间算法和完全多项式时间近似策略(fully polynomial time approximation scheme, FPTAS)。Liang等[9]研究了带有简单线性恶化效应与成组技术的单机资源分配问题,对于极小化加权最大完工时间与资源分配费用之和问题,给出了伪多项式与分枝定界算法。对于同时考虑恶化效应与拒绝惩罚的模型,Nian和Mao[10]研究了单机排序问题,通过将其转化为指派问题及设计动态规划算法,分别证明了在2种恶化加工时间模型下,总完工时间与总拒绝惩罚之和问题可以在多项式时间内求解;Li等[11]研究了平行机排序问题,目标函数为最大完工时间与总拒绝惩罚之和,给出了动态规划算法和FPTAS。Koulamas和Kyparisis[12]研究了安装时间与已完工工件的加工时间有关(p-s-d)且安装时间带有学习效应的单机排序问题,目标函数分别是最大完工时间、总完工时间、总完工时间绝对差以及后2个目标函数的线性组合,给出了多项式时间算法。Huang等[13]研究了带有p-s-d安装时间、恶化效应依赖于时间和学习效应依赖于位置的单机排序问题,对于最大完工时间、总完工时间等目标函数,分别给出了多项式时间算法。Biskup和Herrmann[14]研究了带有p-s-d安装时间的单机排序问题,目标函数是关于工期的函数。Soroush[15]研究了带有p-s-d安装时间和学习效应的单机排序问题,目标函数分别是最大完工时间、总完工时间、总延误、总完工时间绝对差以及提前、延误、相同工期惩罚的线性组合,给出了分枝定界法。Wang等[16]研究了带有拒绝、恶化效应与p-s-d安装时间的单机排序问题,目标函数分别是最大完工时间、总完工时间、总完工时间绝对差以及总等待时间绝对差与总拒绝惩罚之和,给出了多项式时间算法。

1 问题描述

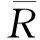
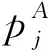
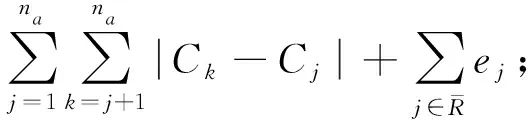
2 理论推导

设C[j]表示排在第j个位置工件的完工时间,W[j]表示排在第j个位置工件的等待时间。

1)Cmax的推导公式:

因此

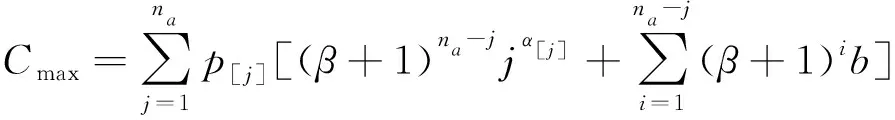
(1)

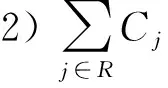
即

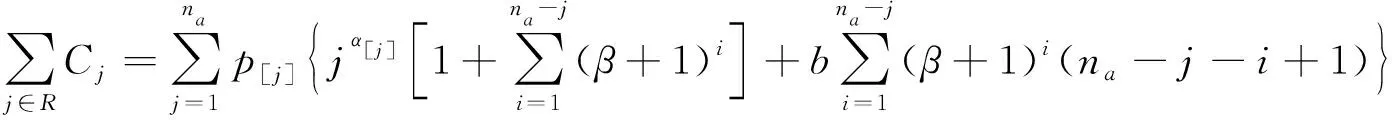
(2)

3) TADC的推导公式:

其中

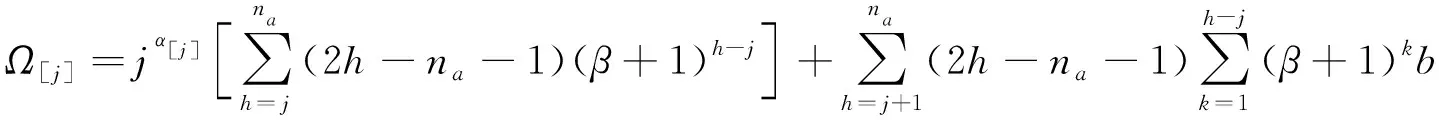
(3)

4) TADW的推导公式:

那么

其中

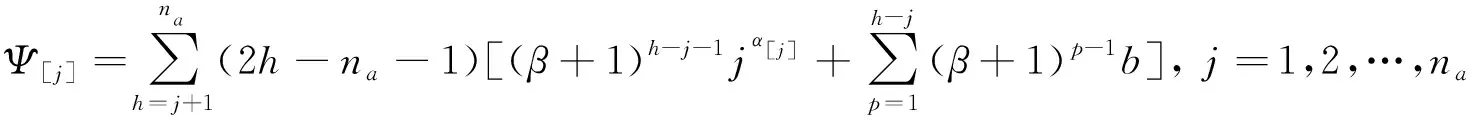
(4)

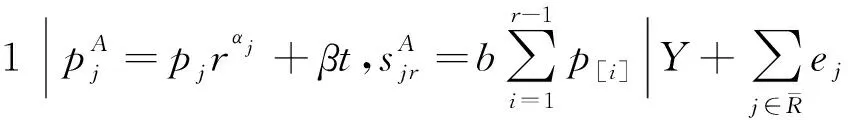
证明 设接受工件的数量为na,下面证明4个目标函数对应的4个问题可以转化为指派问题求解。

1) 当Y=Cmax时,由式(1),令

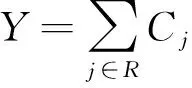
供给侧结构性改革的五大重点任务是去产能、去库存、去杠杆、降成本、补短板。具体来说就是从生产领域入手，减少无效供给，扩大有效供给，提高全要素生产率，使供给体系灵活适应需求结构变化。健身休闲产业供给侧结构性改革的目标就是要从供给的角度，优化资源、人力、资本、技术、政策等要素资源配置，激发政策导向优势，强化资源支撑地位，融入科技与“互联网+”信息技术，推动体育健身休闲产业的可持续发展。结合自治区的《实施意见》，广西健身休闲产业供给侧结构性改革可从供给什么、谁来供给、如何供给、供给环境四个方面（如图1）入手。

3) 当Y=TADC时,由式(3),令

4) 当Y=TADW时,由式(4),令

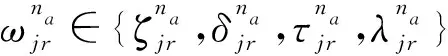
3 算法算例

算法:

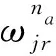
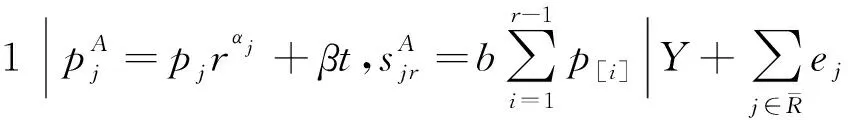
证明 算法的第1步为计算O(n);当na给定时,求解指派问题的复杂度为O(n3),第2步共需解n-1个指派问题,复杂度为O(n4);第3步为O(n),故算法的复杂度为O(n4)。

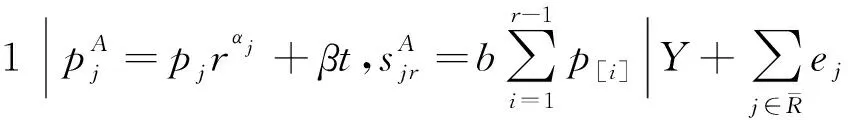
求解:

当na=1时,依次将4个工件放到第1个位置,其余工件拒绝,分别计算目标函数值进行比较,得到接受工件为1或3最好,目标值Z(1)=39;

当na=2时,有

通过指派问题求解,得到接受工件为2和3,S=[3,2],目标值Z(2)=35;

当na=3时,由指派问题整理可得接受工件为2,3和4,S=[3,2,4],目标值Z(3)=48;

当na=4时,由指派问题整理可得S=[1,3,2,4]或S=[3,1,2,4],目标值Z(4)=120。

综上,最优解是接受工件2,3,S=[3,2],最优目标函数值Z*=35。同理可以求得下面问题的最优解。

4 结 语

本文研究了带有拒绝效应的单机排序问题,工件的加工时间同时受到2种恶化效应的影响,即依赖位置和开始加工时间的恶化效应,且工件在加工之前还带有一个p-s-d安装时间。对于4种目标函数,给出了复杂度为O(n4)的多项式时间算法。对于带有恶化效应、安装时间和拒绝的此类问题,今后可以考虑不同的处理机环境或其他类型的恶化效应和安装时间模型。