不同纤维含量的混凝土材料力学特性研究

马宝华

(甘肃省民乐县水务局 张掖 734500)

0 引言

近年来，随着水利工程等领域的快速发展，对水利工程材料性能的要求越来越高，尤其在轻质量和高强度这两个方面最为突出，因此越来越多的纤维复合材料被研发与应用。 杨雨山等[1]研究表明，在抗折强度方面，玄武岩纤维比聚丙烯纤维表现好，而碳纤维的表现最好。韩珀[2]研究发现，聚乙烯醇纤维的抗弯性能比聚丙烯纤维要好，同时纤维掺量对混凝土力学性能也有所影响。蔡娜[3]研究表明，聚丙烯纤维掺量1.2%～1.6%时，抗压强度有所下降。方圣恩等[4]研究表明，当玻璃纤维掺量0%～20%时，随掺量增加混凝土抗压强度呈上升趋势，当掺量超20%时强度下降。李坤[5]研究表明，混凝土抗压、抗折强度随玄武岩纤维掺量的增加而增加。许多研究表明，纤维种类、掺量及其分散性均会影响混凝土的力学性能。为进一步分析纤维混凝土的力学性能，采用数值模拟的方法进行研究。由于数值方法相对于试验而言，能极大地节约成本以及模拟更加复杂的情况。因此，基于前人的相关研究，本文通过有限元方法，对不同碳纤维掺量下混凝土抗压和抗折性能进行研究。

1 试验内容

通过有限元软件中Material的材料设计功能，对无掺量的水工混凝土、1%碳纤维的水工复合混凝土、2%碳纤维的复合混凝土通过Materials中的性能分析功能，确定其基本物理性质，通过加高强度纤维材料提升材料特性来实现纤维混凝土的模拟[6]。材料物性参数如表1所示。

表1 材料物性参数

通过对不同掺量的混凝土进行合成，可以发现：随着碳纤维含量的增加,弹性模量会发生较大变化;由于碳纤维密度较小，整体的密度呈现下降趋势;泊松比和剪切模量变化较小。

图1 碳纤维复合混凝土

2 有限元数值模拟分析

计算机模拟技术在材料设计领域的应用日益广泛，在试验相对麻烦且成本较高的情况下，采用数值模拟分析，可以提高试验的成功率。数值模拟主要是利用一组控制方程(代数或微分方程)来描述一个过程的基本参数变化关系，采用数值计算的方法求解,以获得该过程(或一个过程的某一方面)的定量认识,及对过程进行动态模拟分析,在此基础上判断工艺或方案的优劣、预测缺陷、优化工艺等。数值模拟的基本特点是将微分方程边值问题的求解域进行离散化,在边界上满足边界条件解析解的要求变为求在给定的离散点(节点)上满足由场方程和边界条件所导出的一组代数方程的数值解。

2.1 基于有限元的抗压数值分析

将有限元Materials合成的复合混凝土设计150mm×150mm×150mm的标准试件进行抗压强度分析，试件底面进行固定，对试件中的点进行监测，如图2所示。

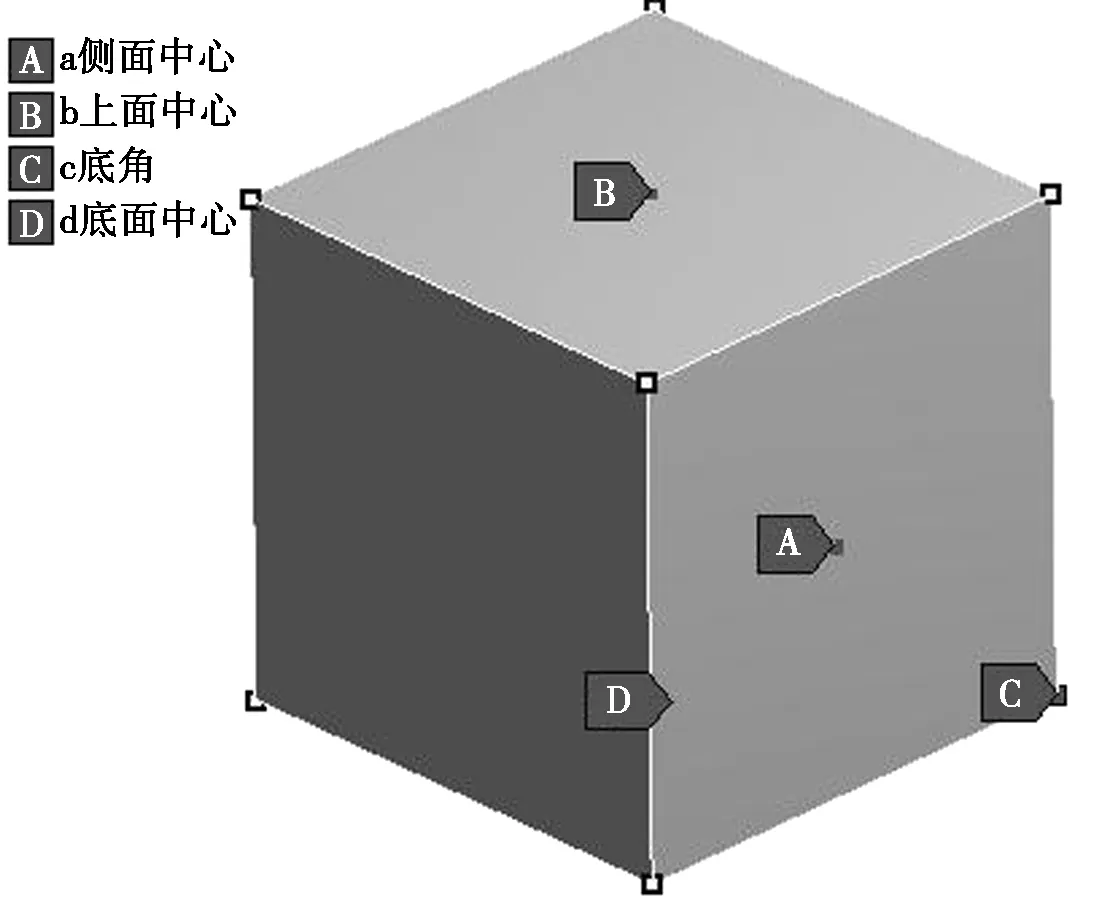
图2 试件监测点

本试验采用瞬态动力学设计能便于观测各监测点在受力过程中应变的变化情况。

试验设计：对顶面施加0.2MPa的压力持续100s，并满足网格无关性要求。

图3为试件在抗压试验过程中的应变情况，可以发现，试件在固定面的四个顶点处应变最大。

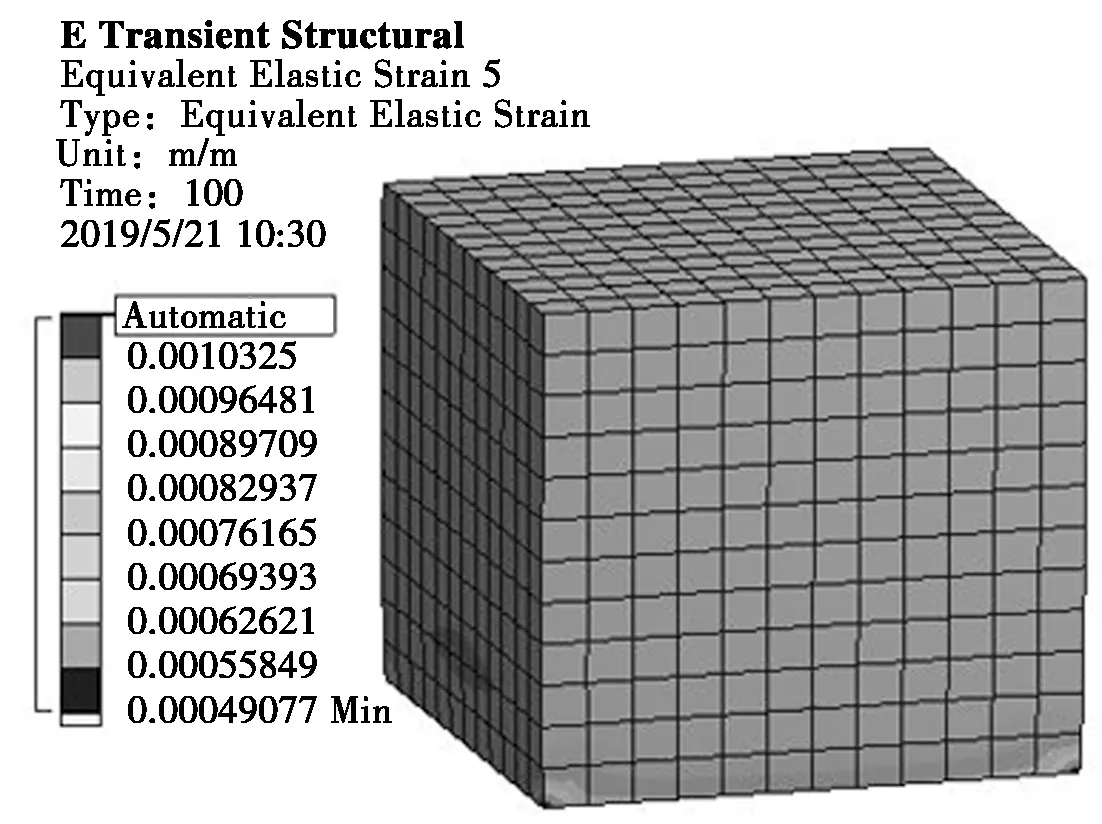
图3 试件抗压应变云图

为了研究不同纤维掺量对混凝土应力应变曲线的影响，通过对不加纤维和纤维含量1%、2%时的碳纤维混凝土试件进行分析，同时对监测点应力应变曲线进行观测，如图4所示。

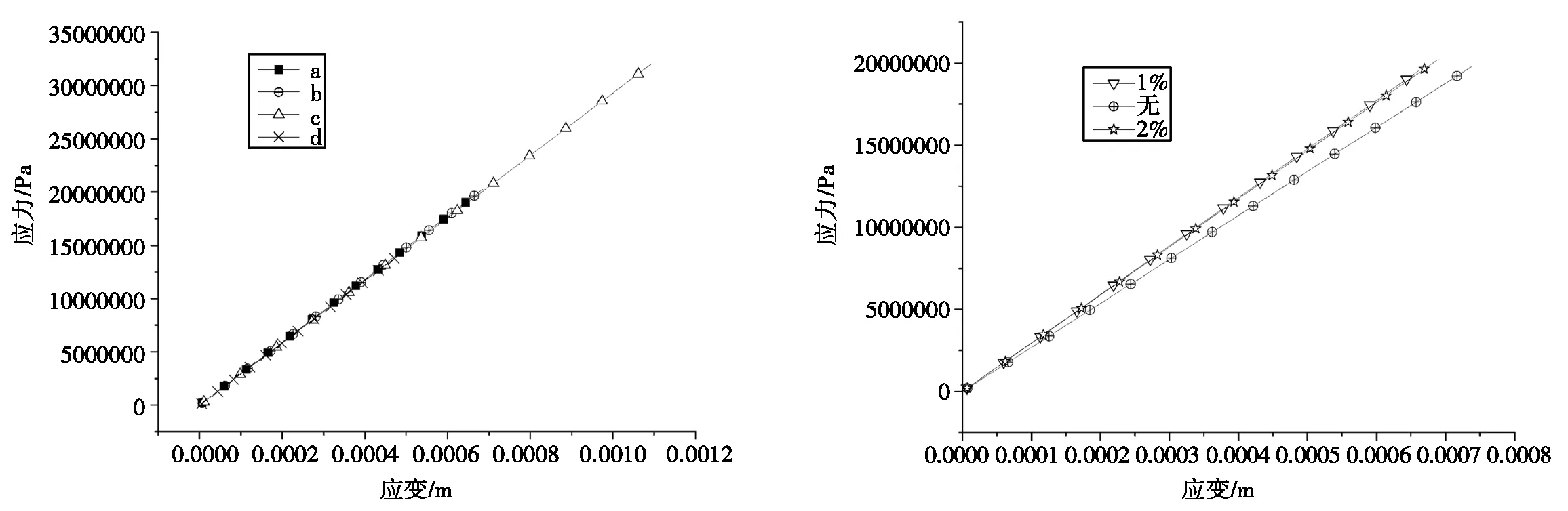
图4 抗压强度试验1%掺量下监测点应力应变曲线与同一监测点不同掺量的应力应变曲线

通过同一试件不同监测点的应力应变曲线和不同材料同一监测点的应力应变曲线，可以发现：同一种材料的各个监测点尽管受力情况有所不同，但其应力应变曲线基本相同，掺入纤维和不加纤维的情况相比，加入纤维之后的抗压强度明显增强，但是1%和2%纤维掺量下并没有明显的变化。因此对于纤维混凝土应合理控制纤维掺量，以防止在满足抗压强度的条件下造成不必要的材料浪费。

2.2 基于有限元的抗折强度试验分析

在瞬态动力学试验过程中采用150mm×150mm×550mm的试件，一端固定约束另一端施加0.2MPa压力，持续施加100s。试验满足网格无关性的要求，在其中选取两个监测点如图5所示，得到如图6的抗折应变云图。

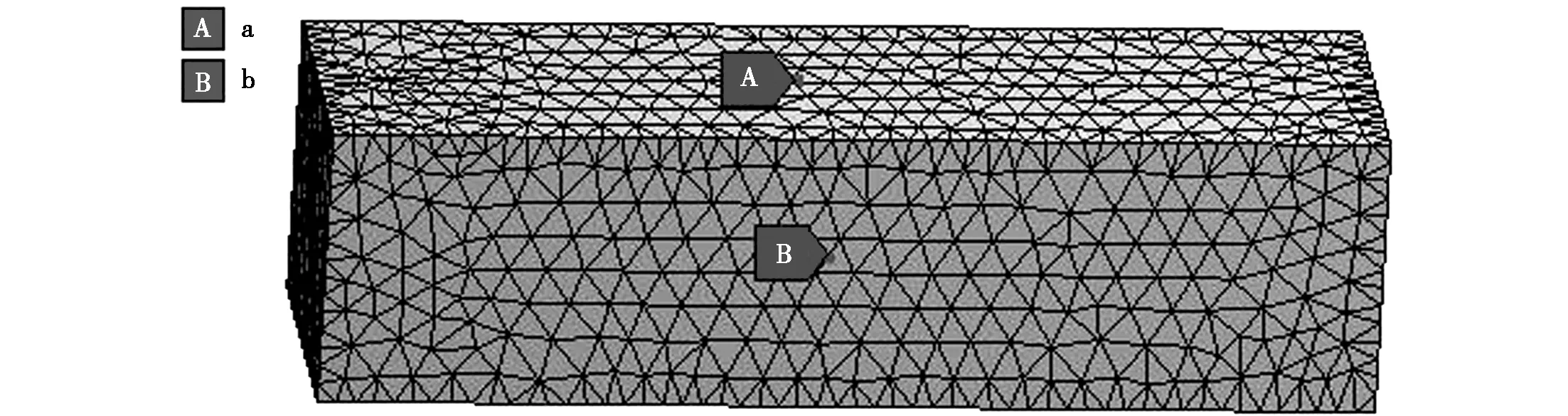
图5 抗折试验网格以及监测点

图6 抗折试验应变云图

由图6可知：中部应变较小两边应变比较大，为了进一步了解持续压力作用下不同掺量试件的变化情况，对试件中a、b进行应力应变曲线监测，如图7所示。

由图7可知：同一试件各监测点受到的应力可能不同，但其应力应变曲线基本相同，同时对不同掺量的混凝土选取同一监测点进行分析，可以发现不同纤维掺量下的混凝土试件在抗折性能方面变化不明显。

图7 抗折试验1%掺量下监测点应力应变曲线与同一监测点不同掺量的应力应变曲线

3 讨论

研究发现不同纤维掺量下的混凝土呈现出不同的力学特性，但力学性能并未因纤维含量的不同呈现出相关性。同时，在抗折强度方面并没有呈现出增强作用，这基本上与李京军和王建超[7-9]研究结果相似，主要是混凝土自身结构原因。在复合力学理论中,碳纤维混凝土被看作是一种纤维强化作用体系。碳纤维混凝土的应力、弹性模量和强度是根据混合原理推算得出的。根据纤维在纤维基体中的分布与取向引入纤维方向系数,正确选择纤维方向系数是决定纤维增强效果的主要因素之一。在纤维间距理论中,是根据线弹性断裂力学原理来解释纤维对混凝土裂缝的产生或抑制作用的。混凝土是一种脆性材料,因此要想增强其抗折、抗压、抗拉等力学性能应从纤维分布方向入手,多方向加入碳纤维后使纤维与混凝土裂缝两边之间的黏应力对混凝土裂缝的扩展有抑制作用，从而增加其力学性能。

因此，研究混凝土纤维掺量的变化规律，有利于认识纤维对混凝土力学性能的增强机理，有助于对试验过程进行预测。研究中由于采用有限元理论进行数值模拟及分析，因此不能深入了解界面处的力学性能变化，因此后续考虑通过离散元软件建立纤维混凝土模型，借助MUC动力学插件进行三轴试验模拟，从而更好地了解纤维混凝土的力学性能变化。

4 结语

本文通过对不同纤维含量下混凝土的抗压试验和抗折试验进行分析，可以得到以下结论：

(1)加入纤维之后混凝土的抗压性能呈现增强效果，但随着纤维含量的增加并没有更好的效果出现，因此混凝土中加入纤维会出现峰值的情况。

(2)加入纤维之后的混凝土试件与无纤维混凝土试件的抗折性能要求相同，因此碳纤维并不能增强混凝土的抗折性能。

(3)为了分析纤维混凝土力学性能的增强机理，应考虑纤维分布方向以及采用离散元方法开展进一步研究。