用几何概率确定球内两随机点距离的分布
魏立力, 李晶晶
(宁夏大学 数学统计学院,银川750021)
1 引 言
几何概率是概率论中一个得以充分发展的分支,其中包括了许多有趣的问题[1],也是贯穿高中数学和大学数学的重要内容之一[2]. 其中最著名的问题就是“贝特朗奇论”,该问题引起了学界长时间的广泛讨论[3-4],近年来利用几何概率研究有界凸体,并且在天体物理学、核物理、基本粒子物理学以分子生物学都有应用[5-6]. 三维球体是特殊的有界凸体,其中两随机点距离的概率分布问题非常直观且有趣,但求解需要“运动测度”(kinematic measure) 的概念[5],不适于本科教学. 本文基于几何概率,用初等概率论的方法推导出了球内两随机点距离的概率分布函数、概率密度函数和数学期望的解析表达式. 基于R语言,对单位球内两随机点之间距离进行了模拟,模拟结果与理论分析结果互为印证, 所得结果适合于本科概率论研究性学习和教学的素材.
设空间坐标系中任意两随机点为P1(X1,Y1,Z1)和P2(X2,Y2,Z2), 三维随机变量(X1,Y1,Z1)和(X2,Y2,Z2)均服从球内的均匀分布, 且相互独立. 令D=|P1P2|表示两点P1和P2之间的距离,问题就是要求D=|P1P2|的分布函数
(1)
下面从理论推导和随机模拟两个不同的视角研究这一问题.
2 分布函数的推导
不妨先考虑单位球,显然D=|P1P2|的支撑集为 [0,2],所以当x<0时,FD(x)=0;当x≥2时,FD(x)=1.下面主要讨论当0≤x<2时,FD(x)的表达式. 首先引入如下结论:
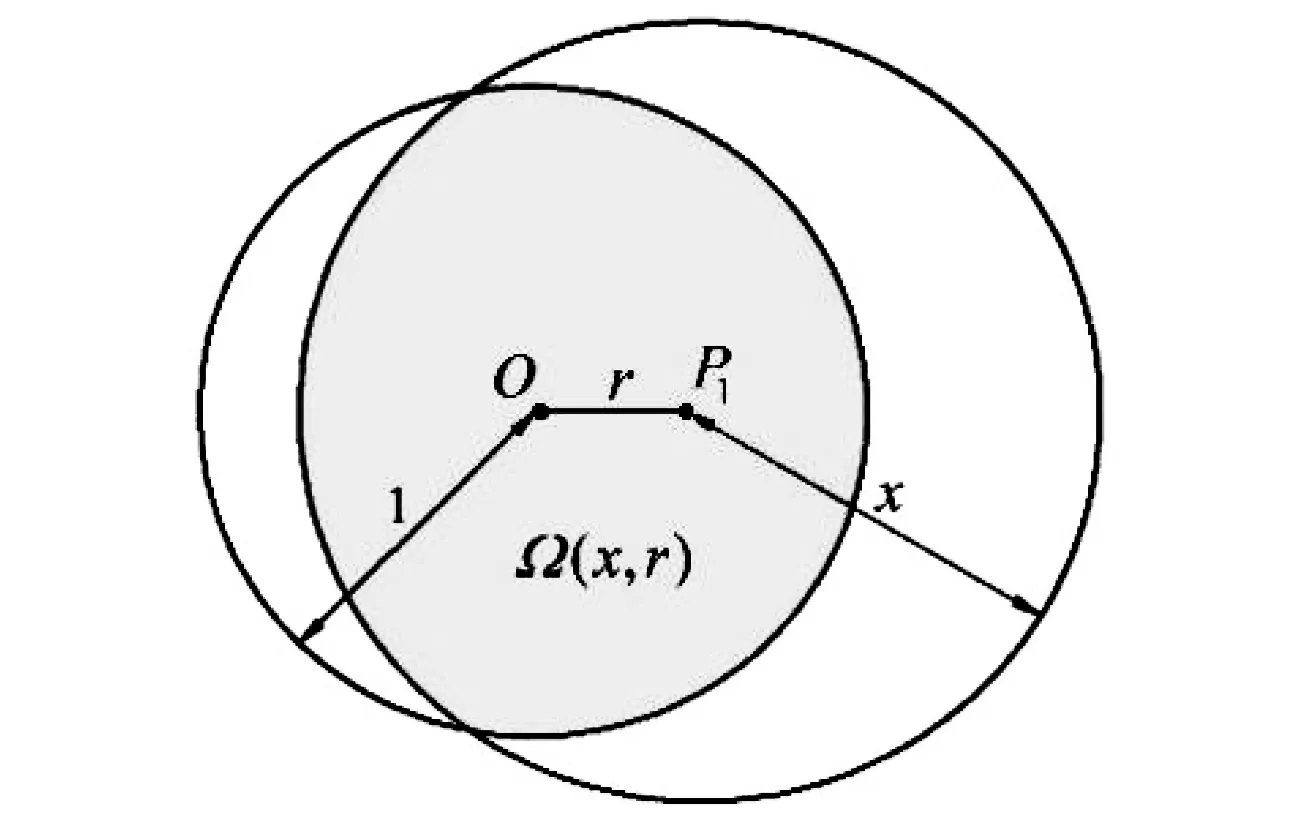
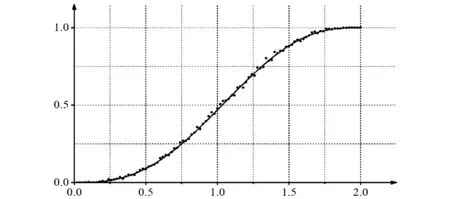
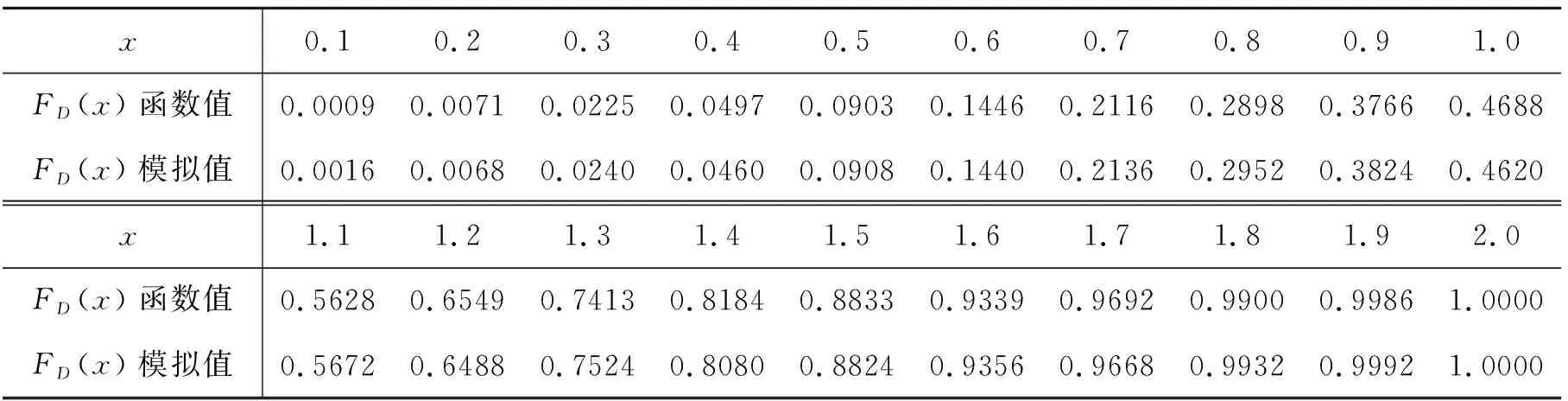
引理1两个半径分别为r1和r2的球,其球心距离为r,则当|r1-r2| (2) 图1 两个球体相交部分的体积(平面图代替) 有关参数如图1所示(用平面图代替了立体图),注意到两个球体相交部分是两个同底球缺, 由球缺的体积公式以及两个球缺之间的关系,可以导出本引理结论,推导过程并不平凡,但属于初等方法,此处省略. 该引理可用初等概率论的知识直接计算得到,此处省略证明过程. 由于P1(X1,Y1,Z1)和P2(X2,Y2,Z2)都服从单位球内的均匀分布,且相互独立,因此 f(rsinθcosφ,rsinθsinφ,rcosθ) 这里用了对称性,此概率只与r有关,与θ,φ无关,因此,有 (3) 其计算就是一个几何概率问题. 设 Ω={(u,v,w)∶u2+v2+w2≤1},Ω(x,r)={(u,v,w)∶(u-r)2+v2+w2≤x2}∩Ω. 图2 阴影部分为区域Ω(x,r) 的示意图(平面图代替) (4) P(D≤x|R=r)=1. (5) 情形三当x,r取其他值时,这时两球相交,由引理1可知,相交部分的体积为 相应的几何概率为 (6) 将公式 (4),(5),(6) 代入公式 (3) 可得,当0≤x<1时, 当1≤x<2时, 这样就得到如下结论: 定理1设P1(X1,Y1,Z1)和P2(X2,Y2,Z2)独立同分布于单位球内的均匀分布,D=|P1P2|是P1,P2的距离,则D的分布函数为 对应的概率密度函数为 如果将单位球换成半径为R的球,则有如下结论. 推论1设P1(X1,Y1,Z1)和P2(X2,Y2,Z2)独立同分布于半径为R的球内的均匀分布,D=|P1P2|是P1,P2的距离,则D的分布函数为 对应的概率密度函数为 下面基于R语言对单位球内两个随机点之间距离进行模拟. 采用筛选法产生单位球内的均匀分布随机点,具体而言算法如下. Step1: 产生区间[-1,1]上的三个随机数X,Y,Z; Step2: 如果X2+Y2+Z2≤1,则P=(X,Y,Z), 并停止;否则返回 Step1. 按照上述算法一次产生服从单位球内均匀分布的两个随机点,计算两点的距离D,对于给定的一个数0 图3 随机变量D的分布函数(光滑曲线)和随机模拟值 表1是FD(x)的函数值和模拟值在x的一些值处的结果,可以看出两者一致. 表1 分布函数FD(x)精确值和随机模拟值的比较 几何概率是概率论中一个经典而充满活力的内容,蒲丰投针及贝特朗悖论都是人们熟知的几何概率问题. 从本质上讲几何概率是计算两个几何体的某种测度之比,为此数学家们发展了积分几何的理论[7],并且在天体物理学、核物理、基本粒子物理学以分子生物学都有应用. 几何概率的特点之一是问题描述比较简单,但求解不易,计算机模拟技术为几何概率的计算提供了强有力的技术路径. 本文实际上是先作了随机模拟,发现模拟的分布函数呈现非常光滑的趋势,从而猜测分布函数有比较简单的解析解,最终理论分析结果和模拟结果达到了互为印证. 本文方法与已有文献相比, 问题的提出与建模、分布函数(概率密度函数)的求解、模拟验证等环节只需要初等概率论的知识, 避开了运动测度 (kinematic measure) 的概念, 很适合于本科概率论研究性学习和教学的素材,通过随机模拟和理论分析的相互印证,可以更好的理解随机性思想. 致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见. 附录:随机模拟的R程序 prob_simu<-function(d=1,n=2000){ i<-0 l<-list(x=numeric(0),y=numeric(0),z=numeric(0)) while(i x<-runif(3,-1,1) if(x[1]^2+x[2]^2+x[3]^2<1){ i<-i+1 l$x[i]<-x[1];l$y[i]<-x[2];l$z[i]<-x[3] } } x<-l$x;y<-l$y;z<-l$z i<-1;k<-N<-0 d2<-numeric(0) for (i in seq(1,n-1,by=2)){ N<-N+1 d2[N]<-(x[i]-x[i+1])^2+(y[i]-y[i+1])^2+(z[i]-z[i+1])^2 if(d2[N]<=d^2) k<-k+1 i<-i+2 } list("simu_value"=k/N,"mean_distance"=mean(sqrt(d2)),"N"=N) } x<-seq(0,2,0.02) y<-mean_distance<-N<-numeric(0) for (j in 1:length(x)){ r<-prob_simu(x[j]) y[j]<-r$simu_value mean_distance[j]<-r$mean_distance N[j]<-r$N } f<-x^3-(9/16)*x^4+(1/32)*x^6 plot(x,y) lines(x,f,lwd=2, col="red") simu_expect<-mean(mean_distance);simu_expect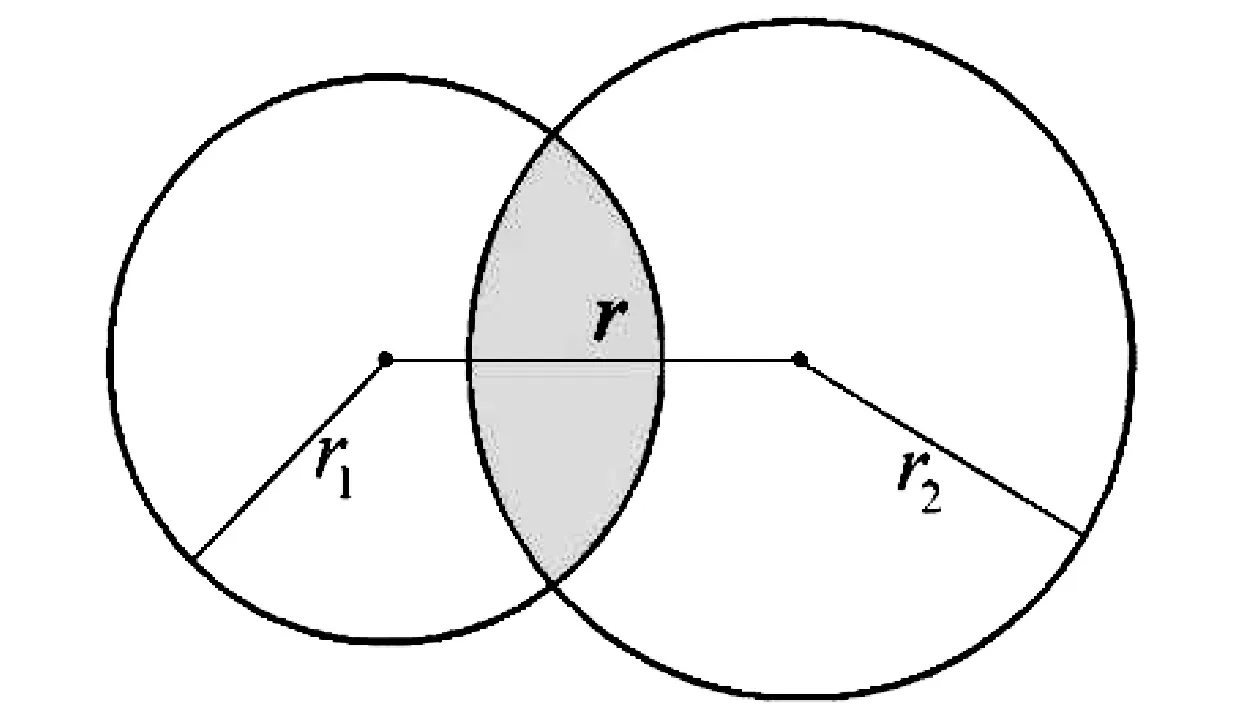
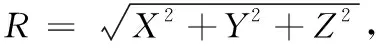

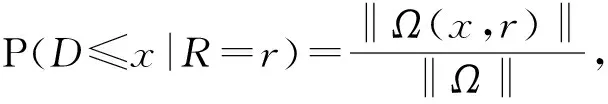

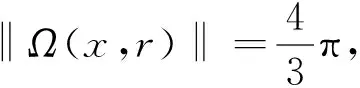




3 单位球内两随机点距离的随机模拟

4 结 论

