脉冲噪声环境下的韧性多径时延估计算法

陈 梦，行鸿彦，王海峰

(南京信息工程大学江苏省气象灾害预报预警与评估协同创新中心，江苏 南京 210044)

0 引言

信号源到各个接收器的距离不同会使得信号到达各个接收器的时间不一致，产生时间差，时间延迟估计就是运用信号处理的方法估计出这个时间差，根据估计出的时间差可以确定辐射源的位置[1]。在实际环境中，信号的传播经常会受到多径干扰[2]的影响，使得接收信号中包含发射信号的多径副本信号，对多径传播的接收信号进行参数估计在雷达、声纳、移动通信等领域有着广泛的应用[3-5]，因而对其研究十分重要。传统基于相关分析的多径时间延迟估计方法[6]分辨能力受带宽限制，不适用于多径信号时延差小于信号带宽倒数的情况，目前，高分辨率是多径时延估计的研究重点。

经典的高分辨多径时延估计算法主要有期望最大化算法(expectation maximization algorithm，EM算法)[7]，多重信号分类算法(multiple signal classification，MUSIC)[8]，利用旋转不变技术的信号参数估计技术(estimating signal parameters via rotation invariance techniques，ESPRIT)[9-10]和WRELAX算法(weighted fourier transform and relaxation based method，WR算法)[11]等。其中，WR算法因其准确率高、拓展性较好的特点受到学者的广泛关注。经典的WR算法将背景噪声建模为高斯分布，而在很多实际应用环境中如水声通信、无线通信、生物医学测量等，信号在传播过程中易受到突发性脉冲噪声干扰，此时将背景噪声建模为高斯分布与实际不符。对称Alpha稳定分布(symmetricα-stable distribution，SαS)是一种广泛使用的可以描述这类背景噪声的极限分布[12]，α(0<α≤2)作为其特征指数，表示随机信号的脉冲程度，α取值的大小与脉冲性呈反比，α取最大值2时SαS分布退化为高斯分布。SαS分布只有小于α阶的矩有限，所以基于二阶统计量的WR算法在α取值小于2时的SαS分布噪声环境下性能退化。

分数低阶统计量理论(FLOS)由二阶统计量理论发展而来，学者们将FLOS引入现有的高分辨多径时延估计算法，可以提高多径时延估计算法抵御脉冲噪声的能力，解决在SαS分布噪声环境下经典算法性能退化的问题。针对WR算法，文献[13]应用FLOS中的共变概念和最小分散系数准则对其进行改进，提出了一种韧性的高分辨率多径时延估计方法(称为P-WR算法)；但是基于FLOS的多径时延估计算法其阶数P的取值必须小于SαS分布的特征指数α，且满足1≤P≤2，而实际应用中SαS分布的特征指数难以获得，依据接收信号对其进行准确估计也并非易事。

本文针对脉冲噪声环境下基于二阶统计量的WR算法性能退化,采用分数低阶统计量理论改进后的P-WR算法对脉冲噪声先验知识依赖性过高的问题，提出基于Sigmoid变换和相关熵的韧性多径时延估计算法(sigmoid and correntropy based weighted relaxation，SCWR)。

1 相关熵理论

相关熵是一种既能刻画随机过程时间结构又能描述随机过程统计分布的统计量，其通过非线性映射将时域的非线性问题转换到再生核希尔伯特空间进行求解，与相关函数相比，可以抑制突发性脉冲噪声对整个算法的影响。

任意两个随机变量X和Y之间的相关熵定义为[14]：

Vσ(X,Y)=E[kσ(X,Y)]

(1)

式(1)中，E[·]表示数学期望，kσ(X,Y)表示满足Mercer条件[15]的高斯核函数，σ>0表示高斯核的核长，如式(2)所示：

(2)

(3)

从相关熵定义中可以诱导出一个距离度量即相关熵诱导距离(correntropy induced metric，CIM)[16]，其表达式如式(4)所示：

CIM(X,Y)=[Kσ(0)-Vσ(X,Y)]1/2

(4)

基于CIM距离测度，定义最大相关熵准则(maximum correntropy criterion, MCC)为：

MCC(e)=maxE[kσ(e)]，e=X-Y

(5)

式(5)中，误差e越小则相关熵越大，表明随机变量X与Y的相似性越高；反之e越大，相关熵越小；当e大于受核长控制的某一阈值时，相关熵逼近于0。也就是说相关熵是一种“局部测量”方法，测量随机变量之间的相似性时，只有受核函数约束的样本能明显影响相似性度量结果。这也是相关熵能够抑制脉冲噪声的直接原因。

2 韧性多径时延估计算法

2.1 多径信号模型

假设信源已知，则多径传播的接收信号可以表示为：

(6)

式(6)中，L为多径传播的路径数目；al和τl分别为各路径的衰减系数和时间延迟；s(k)表示信号源；w(k)为服从SαS分布的加性噪声，并且它们互不相关。

2.2 Sigmoid变换

Sigmoid变换是一种常用于抑制脉冲噪声的非线性预处理方法[17]，其数学表达式如下：

(7)

式(7)中，n为离散时间变量。Sigmoid函数曲线如图1所示。

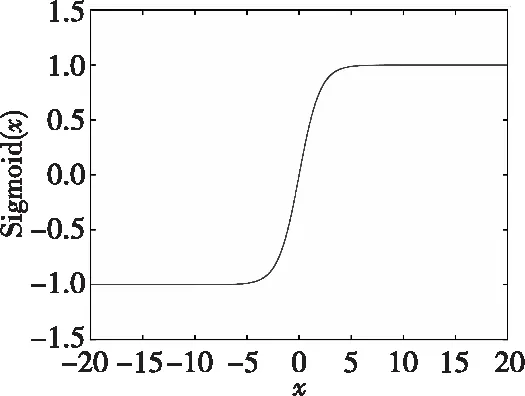
图1 Sigmoid函数曲线Fig.1 Sigmoid curve

Sigmoid函数对于不同幅度的输入信号，有不同的输出效果。图1中，当输入信号幅度较小时，近似于线性变化；当输入信号幅度较大时，具有抑制作用，是一种非线性变化。运用Sigmoid函数对多径传播的接收信号进行预处理，初步抵御了脉冲噪声对算法的影响，并且不影响接下来对有用时延信息的提取，实际应用中可以跟据接收信号调整曲线参数。

2.3 WR算法

对于式(6)的多径时延估计问题，从理论上可以求一个最小二乘解，即：

(8)

将背景噪声建模为高斯分布时，式(8)等同于求解参数的最大似然估计，因而多径时延估计问题转换为参数估计中的多维最优化问题。

WR算法是一种可以有效解决式(8)的多维最优化问题的参数估计算法。该算法的核心为松弛搜索思想，其基本内容是首先分解代数微分方程组成的系统，分解成多个子系统后，再分别求解每个子系统。求解每个子系统时，把其他子系统前一次的迭代值当作猜测值用于求解当前子系统，然后把解出的值再当作其他子系统的猜测值，重复以上过程，直至算法收敛。

WR算法解决多径时延估计问题时，其步骤如下：

1)假设观测信号的矢量为：

r=[r(1),r(2),…,r(N)]T

(9)

源信号到达观测点的L个径的信号矢量设为：

Sτl=[s(1-τl),s(2-τl),…,s(N-τl)]T,l=1,2,…,L

(10)

观测信号的背景噪声矢量为：

w=[w(1),w(2),…,w(N)T]

(11)

高斯噪声环境下代价函数写为：

(12)

2)利用松弛搜索思想求解式(12)的多维最优化问题。假设所有L条多径中，只有第k条是未知的，其余L-1条均已知，则可令第k条多径信号为：

(13)

那么式(12)的代价函数可写为：

Ck(ak,τk)=‖rk-aksτk‖2

(14)

(15)

(16)

式(15)和(16)中，sτ=[s(1-τ),s(2-τ),…,s(N-τ)]T。

2.4 SCWR算法

SCWR算法的基本思路如下：首先采用式(7)的Sigmoid函数对多径传播的接收信号进行非线性变化；然后，在WR算法的理论基础上，利用最大相关熵准则结合松弛搜索思想，估计出多径时延值。

利用最大相关熵准则解决式(6)的多径时延估计问题，即：

(17)

(18)

用最大相关熵准则代替WR算法中的最小均方误差准则，将式(14)的代价函数替换为：

Ck(ak,τk)=E[kσ(rk-αksτk)]

(19)

(20)

(21)

其中，式(20)和式(21)中的ak已知，在初次迭代时为设置的衰减系数初值，在第m次迭代时为第m-1次的估计值，式(21)中运算符⊙表示两矢量对应位置的元素相乘。

SCWR算法的实现步骤如下：

1)对多径传播的接收信号按式(7)进行非线性变化。

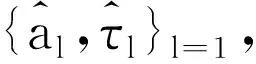
3 算法仿真

为验证所提算法的多径时延估计性能，本文进行了四组实验，其中，将WR算法和P-WR算法作为参考算法，比较分析了本文算法的优越性。

3.1 性能评价指标

本文采用均方根误差(root mean square error, RMSE)和平均准确率PA衡量所提算法和参考算法的估计性能。评价指标的表达式定义为：

1)均方根误差

(22)

2)平均准确率

(23)

3.2 仿真实验

实验1 将SαS分布的特征指数α设定为1.4，选取不同的广义信噪比GSNR，比较WR算法、P-WR算法和SCWR算法时延估计性能。P-WR算法中的参数P=α-0.1，SCWR算法中的核长σ=10。仿真结果如图2所示，在给定特征指数的SαS分布噪声环境下，WR算法与使用了脉冲噪声抑制技术的P-WR算法和SCWR算法相比，性能较差。SCWR算法在GSNR>-2 dB时均方根误差为0，平均准确率100%，而P-WR算法在GSNR>2 dB时才能达到同样的估计精度。因此，在相同特征指数的SαS分布噪声环境下SCWR算法的估计性能优于WR算法和P-WR算法。

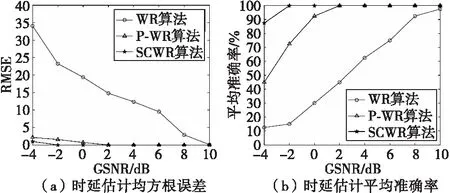
图2 不同广义信噪比下各算法的估计性能Fig.2 Estimation performance of each algorithm under different GSNR

实验2 将广义信噪比GSNR设定为0 dB, 选取不同的SαS分布的特征指数α，比较WR算法、P-WR算法和SCWR算法时延估计性能。P-WR算法中的参数P以及SCWR算法中的核长σ选取与实验1一致。仿真结果如图3所示，WR算法只有在α=2时的高斯噪声环境下能对多径时延做出准确估计，在α<2时性能急剧退化，而P-WR算法和SCWR算法在高斯和非高斯噪声环境下都能较好地估计出多径时延。SCWR算法在不同的特征指数α下的RMSE均为0，平均准确率为100%，而P-WR算法在α<1.8时估计精度逐渐出现偏差，说明SCWR算法对脉冲噪声的适应性要优于P-WR算法。

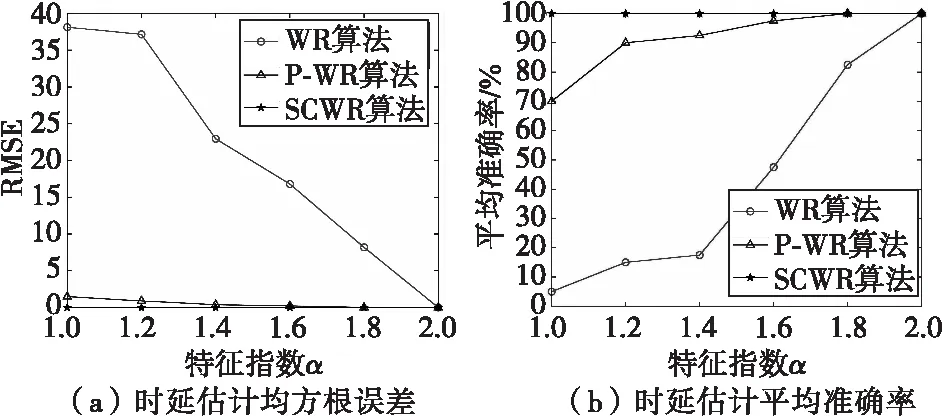
图3 不同特征指数α下各算法的估计性能Fig.3 Estimation performance of each algorithm under different characteristic exponents α

实验3 给定广义信噪比GSNR=-4 dB选取不同的核长参数σ，研究在SαS分布噪声的特征指数α= 1.0、1.5和2.0时，核长参数σ对SCWR算法估计性能的影响。仿真结果如图4所示，在相同广义信噪比和特征指数的SαS分布噪声环境下，可以选定算法的最佳核长参数。由图3(a)可知，特征指数α取1.0和1.5时，核长σ取4可获得最低的均方根误差；α取2时，核长σ取6可获得最低的均方根误差。由图3(b)可知，特征指数α=1.0、1.5、2.0时，核长σ分别取4、8、12，可分别获得87.5%、77.5%和80.0%的最高平均准确率。这是因为相关熵判断“局部相似性”的窗口由核长控制，核长越大则窗口越大，相关熵越近似于相关，其抑制脉冲噪声的能力就越低；核长越小相关熵的相似性判断能力越差，核长太小会使相关熵的使用无意义。虽然SCWR算法核长参数的选取与SαS分布噪声的特征指数α有关，但较之于P-WR算法中分数低阶参数P必须小于特征指数α，SCWR算法对脉冲噪声先验知识的依赖性有所降低。

图4 不同核长和不同特征指数α下SCWR算法的估计性能Fig.4 Estimation performance of SCWR algorithm under different kernel length and different characteristic exponents α

实验4 给定SαS分布的特征指数α=1.4，选取不同的核长参数σ，研究在广义信噪比GSNR=0、-2和-4 dB时，核长参数σ对SCWR算法估计性能的影响。仿真结果如图5所示，核长参数σ=6时，三种广义信噪比下算法均可获得最高平均准确率，说明 SCWR算法核长参数的选取与广义信噪比无关。

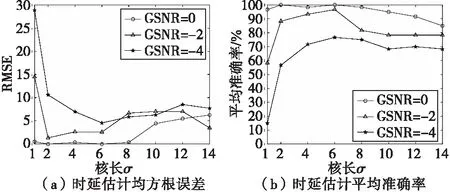
图5 不同核长和广义信噪比GSNR下 SCWR算法的估计性能Fig.5 Estimation performance of SCWR algorithm under different kernel length and different GSNR

4 结论

本文提出一种脉冲噪声环境下的韧性多径时延估计算法(SCWR)。该算法首先采用Sigmoid变换对多径传播的接收信号进行非线性预处理，初步降低脉冲噪声的影响；再运用相关熵理论中的最大相关熵准则,结合参数估计理论中解决最小二乘优化问题的松弛搜索思想对多径时延参量进行估计，用相关熵代替传统互相关，进一步抑制了脉冲噪声对算法的影响。仿真结果表明，该算法估计性能要优于经典WR算法和P-WR参考算法，并且较基于分数低阶统计量理论的P-WR算法，SCWR算法中参数的选取对脉冲噪声先验知识的依赖性有所降低。

该算法在脉冲噪声环境下能较好地估计出多径时延，是一种具有较高韧性的多径时延估计算法,但其参数的选取依旧与脉冲噪声的先验知识有关,后续可针对参数选取作更深入的研究,以提高算法稳定性。