基于变分模态分解的浅层震源聚焦定位方法

赵飞飞，李 剑，王小亮，孙泽鹏，韩 焱

(中北大学信息探测与处理山西省重点实验室，山西 太原 030051)

0 引言

地下浅层震源定位是地下浅层空间研究的热点问题之一, 该方法在地下浅层爆炸、工程爆破、煤矿勘察等方面都具有重要的应用价值[1]。目前浅层定位主要借鉴深层震源定位方法，主要包括以下3种[2]：1)基于走时定位方法；2)基于速度位置联合的定位方法；3)基于逆时偏移的定位方法。由于逆时偏移的定位方法不需要进行走时拾取，且适合处理信噪比低的数据，是近年的研究热点[3]。文献[4]在逆时延拓过程中采用干涉成像条件进行定位，并结合多井联合监测削弱了假象的干扰；文献[5]使用反褶积成像条件，只利用每个传感器记录的波形，逆时聚焦实现震源定位；文献[6]提出了互相关成像条件，消除了时间维度的影响，提高了定位结果的空间分辨率；文献[7]提出多分量加权弹性波干涉成像定位方法，进一步提高了定位精度；文献[8]提出了分组互相关成像条件，通过合适的分组方式提高了成像的分辨率。上述方法在深度震源定位中取得了很好的效果。

然而，由于浅层地层结构复杂，震动波传输信道随时空变化，检测到的震动波具有波形复杂、多频率波形混叠与频散严重等特点,将深度震源定位方法应用于地下浅层定位中，会造成地下浅层震源定位误差较大。为此，文献[9]提出了一种基于逆时能量聚焦的地下浅层震源定位方法，该方法通过振幅叠加，同时添加成像条件生成能量场，利用深度学习进行定位，得到了较高的定位精度。上述方法利用了震动波信号的全谱特征，但由于震源波的带宽较宽，且信号在地层信道传输过程中会产生频散等干扰，影响了定位精度。针对上述问题，本文提出基于变分模态分解(VMD)的浅层震源聚焦定位方法。

1 变分模态分解(VMD)原理

VMD作为一种信号分解估计方法[10]，实质上就是将一个实信号f(t)分解成k个模态频率分量，这些模态频率分量之间相互独立并具有一定的稀疏特性。该算法可分为变分问题的构造和求解两个部分。

1.1 变分问题的构造

变分问题的构造首先对每个模态频率分量进行希尔伯特变换，得到一个单边频谱；接着与e-jωkt混合，将频谱转移到基带；最后通过高斯平滑性估计带宽。变分约束模型的表达式如式(1)所示[11]：

(1)

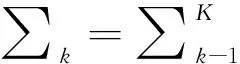
1.2 变分问题的求解

引入二次惩罚因子α和拉格朗日乘数λ，可将上式变为非约束变分问题，表达式如式(2)所示：

(2)

该方法通过迭代搜寻变分模型最优解来确定每个频率分量的频率中心和带宽，从而能够自适应进行信号的稀疏分解[12]，得到最终的{uk}。

针对震动信号的宽频谱和频散的特点， VMD可实现主信号各分量中心频率的自适应提取，实现主信号的有效分离。

2 基于VMD的三维能量场聚焦定位方法

基于VMD的三维能量场聚焦定位方法是利用震动信号的宽频谱特性及高频信号成像的高聚焦特点，首先对各传感器信号利用VMD进行稀疏分解，之后对各频率分量依次运用逆时偏移(RTM)成像方法重构三维能量场，形成高分辨率的三维逆时聚焦能量场图像，最后将计算得到的聚焦区域的重心作为定位结果。三维能量场聚焦定位流程如图1所示。

图1 三维能量场聚焦定位流程图Fig.1 Flow chart of 3D energy field focus positioning

2.1 浅层地层与震源信号的生成

2.1.1浅层地层结构

本文建立长、宽、深分别为100 m、100 m、50 m的监测区域，以西东走向为x轴、南北走向为y轴建立坐标系，(50 m,50 m)地表中心设为坐标原点，在x轴方向等间距布设3个传感器，y轴方向等间距布设4个传感器，形成3×4的传感器阵列，如图2所示。

图2 布设传感器阵列图Fig.2 Layout of the sensor array

2.1.2传感器震源信号的产生

基于传感器阵列中各传感器与震源的距离不一致，其震动信号到达传感器的时间也不一致的思想，本文将经过时移的爆炸震动信号模拟各传感器获取的信号。

传感器获取的信号理论上为震源波经过时间(t1,t2,…,tN)(N为传感器的个数)时移得到的，(t1,t2,…,tN)为震源到各个传感器的时间。当震源在监测区域中心位置时，震源波及部分传感器获取的信号如图3所示。

图3 震源波及部分传感器获取信号Fig.3 Source wave and signals obtained by some sensors

2.2 基于VMD的震动信号分解

根据上述原理介绍，本文采用VMD对模拟震源波进行稀疏分解，震源波形如图4所示。

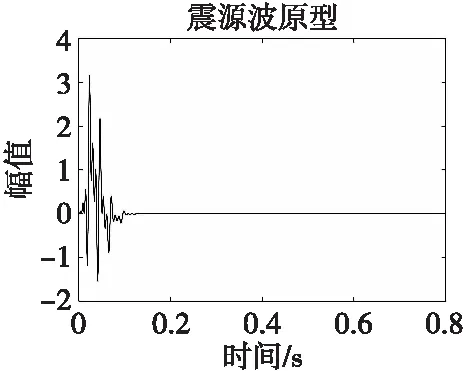
图4 模拟震源波Fig.4 Simulated source wave

采用S变换对其进行时频及频谱分析，结果如图5所示。

图5 震源波时频及频谱图Fig.5 Time-frequency and spectrogram of the source wave

从图5可以清楚地看到模拟震源波信号主要包含4个频率。VMD的k=4，分解结果如图6所示，各分解频谱图如图7所示。

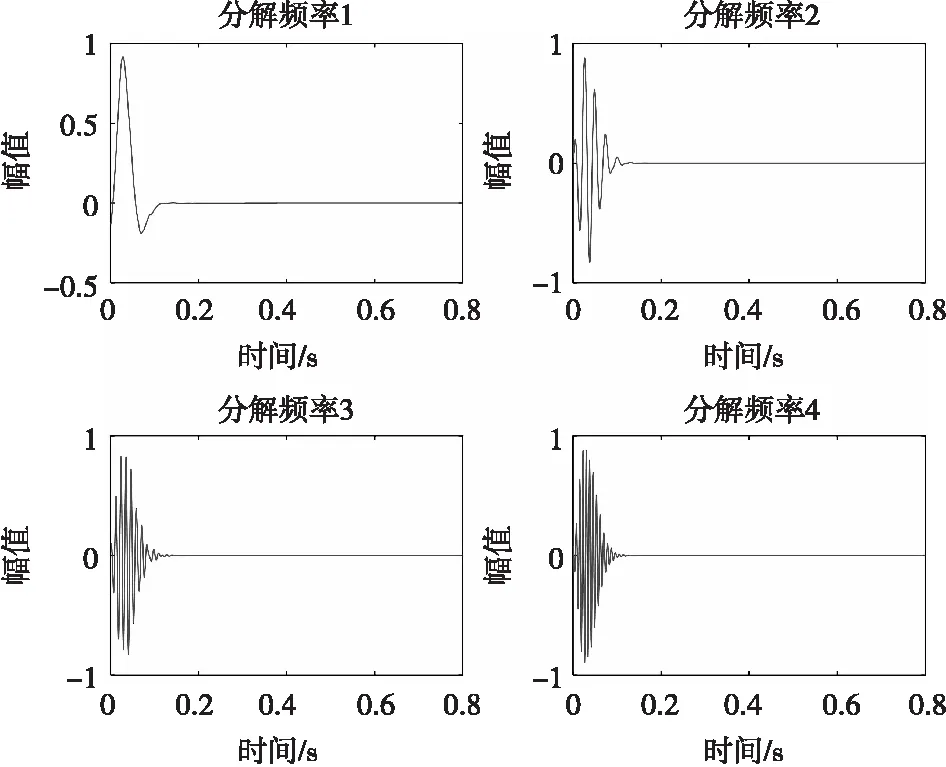
图6 VMD分解结果Fig.6 The decomposition results of VMD

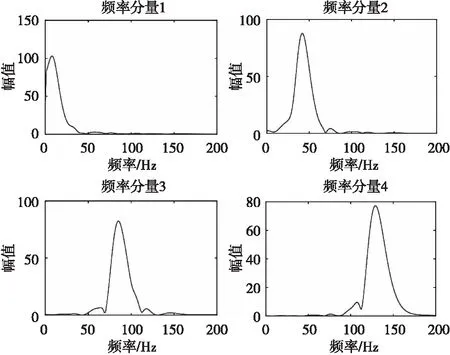
图7 分解结果频谱图Fig.7 Spectrogram of the decomposition result

从图6和图7可以看出，VMD对主信号进行了有效的分离。分解信号之间具有稀疏性，且每个信号的主频率幅值都很突出，几乎没有频率混叠的情况。将分解重构信号与原波形进行误差分析，如图8所示。

图8 误差分析Fig.8 Error analysis

由图8(a)可以看出，分解后的重构波形与原波形在很大程度上都保持一致，只是在波形转折点附近存在较小的偏移。对其采用均方根误差进行分析，如图8(b)可知，均方根误差最大的在0.1左右，且大部分均方根误差都小于0.06，由此可知基于VMD的信号分解具有很高的精度。

2.3 三维RTM聚焦成像

三维RTM聚焦成像是利用每个传感器经VMD分解的各模态频率分量信号分别采用RTM成像，从而形成三维逆时聚焦能量场图像。

RTM成像是利用震动波场的互易性原理，将传感器获取的信号，以逆向传播的方式，并采用互相关成像条件，形成包含震源信息的三维能量场图像[13]，如图9所示，其中聚焦点即为震源位置。

图9 RTM成像示意图Fig.9 The diagram of RTM imaging

具体过程为：对每两个传感器接收到的信号进行互相关，并将结果叠加，得到三维逆时聚焦图像数据体。遍历传感器分解的每一个模态频率分量u1,u2,…,uk)，则得到多谱三维能量场Img1,Img2,…,Imgk)，以Img1为例表达式如式(3)所示：

(3)

式(3)中，X为目标区域中的某一点(x,y,z)，C1(Ri(X),Rj(X))表示第i个和第j个传感器对应u1在该点的互相关波形，N为传感器的个数。

2.4 重心定位

在形成的三维聚焦能量场中，找出聚焦区域集合(x,y,z)，并计算聚焦区域的重心作为最后的定位坐标。具体如式(4)所示：

(4)

3 数值仿真研究

3.1 仿真实验条件设置

为了验证该聚焦定位算法的有效性，进行数值仿真。本文假设炸点坐标为[0,0,-25]m，传感器布设位置及预设震源位置如图10所示。

图10 传感器及震源位置Fig.10 Sensor and source location

3.2 基于VMD分解的三维聚焦能量场

采用图4中VMD 分解的4个模态频率分量依次进行RTM成像，得到多谱能量场及能量聚焦区域，并通过计算聚焦区域的重心确定每个模态频率分量的定位结果，并与直接采用模拟震源波聚焦的效果对比，如图11—图13所示。

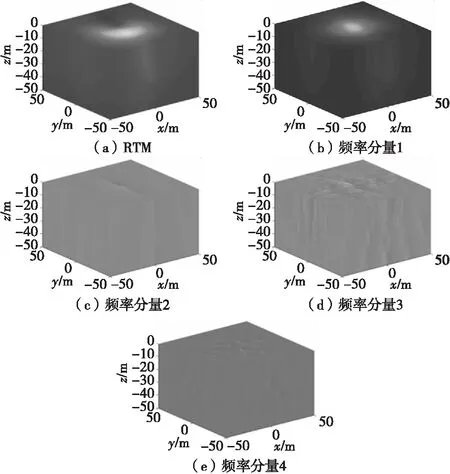
图11 三维能量场成像对比Fig.11 3D energy field imaging contrast

从图11可以看出，经过分解后形成的三维能量场外部能量起伏皆比直接采用震源波形成的能量场要小。进一步，截取震源处切片对内部聚焦效果进行对比，如图12所示。

从图12可以看出随着模态频率分量频率的增加，聚焦区域在依次减小。图12(b)在大体上已经实现了聚焦，但是聚焦区域过大；图12(c)的聚焦区域已经大为减小；图12(d)在图12(c)的基础上更为细致地刻画能量的起伏大小，聚焦区域也更为突出；图12(e)进一步削弱了其他小起伏能量的影响，重点细致地体现了能量聚焦点。由此，更加形象地表现了低频率刻画大体上的聚焦，而高频率则更为细化突出聚焦点，并且都比图12(a)都更接近震源位置，偏移较小。

图12 震源切片处成像对比Fig.12 Imaging contrast at the source slice

从三维聚焦区域大小来对比整体的聚焦效果，如图13所示。

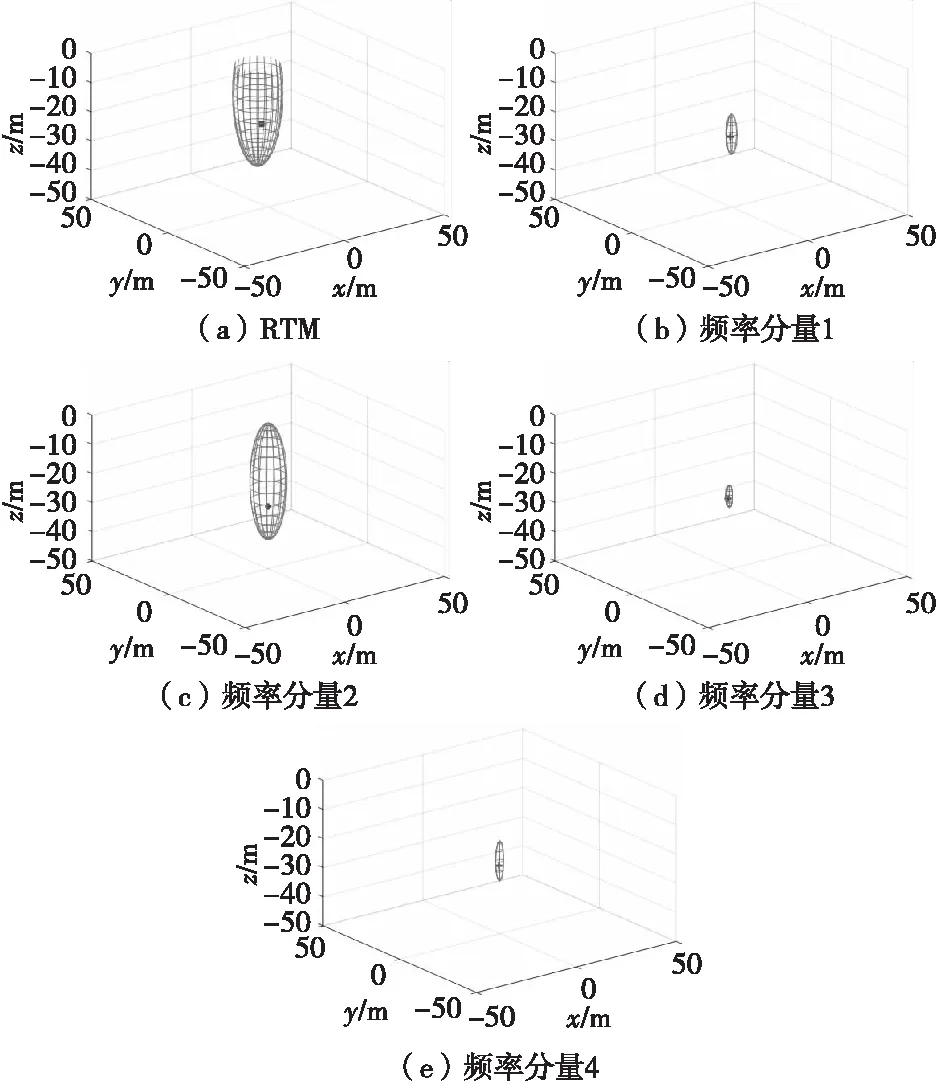
图13 聚焦区域及定位结果Fig.13 Focus area and positioning results

从图13可以明显的看出，每个模态频率的三维聚焦区域都比RTM的聚焦区域小。

同时，本文将能量场聚焦区域占整个能量场的百分比定义为聚焦度，再结合峰值信噪比评价聚焦效果。聚焦度越小聚焦区域越小，峰值信噪比越高聚焦区域越清晰。具体聚焦效果对比如表1所示。

表1 聚焦效果对比Tab.1 Comparison of focusing effect

从表1可以看出，经过VMD分解的每一个模态频率分量的聚焦度都比直接采用RTM成像的小，且峰值信噪比更高。表明通过对信号进行稀疏分解，用分解后的模态频率分量会比原始波形聚焦效果更好、更清晰。

3.3 基于VMD分解的聚焦定位

计算上述聚焦区域的重心作为定位结果，如表2所示。

表2 定位结果对比Tab.2 Comparison of positioning results

从表2可以清楚地看出，与RTM相比，本文经过稀疏分量，采用经VMD分解后的模态频率分量进行聚焦定位的效果更好，定位误差更小。

4 结论

本文提出基于VMD的浅层震源聚焦定位方法。该方法利用爆炸信号的宽频谱特性及高频信号逆时成像更聚焦的优点，反演重建各模态频率分量所对应的三维逆时能量场图像，构建了高精度的能量场聚焦图像，并通过计算聚焦区域的重心得到定位结果。仿真结果表明本方法与RTM相比，成像结果更聚焦且图像更清晰，定位精度也得到了进一步提升。在实际测试中，各传感器信号并不完全一致，但具有较大相关性，通过VMD实现信号主频率成分的有效分离后，仍可实现高精度的震源定位。