粉体颗粒离心压缩仿真及分析

霍 枫，常 颖，陆晓霞，刘英莉，李 聪，鲍邵衡

(国民核生化灾害防护国家重点实验室，北京 102205)

危险化学品泄漏事故的有效处置手段多样，其中非常重要的一种方法是通过喷撒洗消剂来消除染毒体和污染区的毒性危害，该方法不仅可以近距离对污染地面进行洗消，还可以通过投放洗消弹的方式对远距离污染区域进行大面积洗消。在处置过程中，洗消剂的成分及作用方式都会对洗消效果起到关键作用。其中粉体洗消剂因具有较大的比表面积以及对有毒化学品具有较高的吸附-反应能力而受到广泛关注[1]。粉体洗消剂的使用方式是预先将粉体压缩后装填于洗消弹的料筒内，洗消弹被投掷到污染区后，利用气流推喷方式将内部粉体喷出，布撒并覆盖危险化学品表面使其发生反应从而失去危害性。为加强洗消效果，可以采用提高洗消弹料筒内粉体浓度，控制装量精度和均匀性的方法，以达到增大粉体与危险化学品反应量的目的。

为减小粉体装填过程扬尘导致环境污染等问题，常颖等[2]提出了利用离心方式进行粉体气固分离从而提高压缩度的新方法。该方法的工作原理如下：在主轴的带动下，装有粉体的料筒随着吊杯高速旋转。在离心力作用下，料筒从竖直状态变为水平状态，内部的粉体颗粒在高速旋转过程中发生挤压，重新排列，向料筒底部进行压缩，趋向并附着于筒体底部形成具有一定密度的产品。

粉体颗粒具有传统气-固-液态物质所不具备的独特性质，如离散性、非线性响应、自我组织性、高耗散性、力链不均匀等性质，但由于颗粒体系的复杂性，对颗粒物质的有关研究目前仍处于起步阶段[3-4]。对于粉体装填与压缩过程，已有相关文献进行研究，但相关机理尚未得到充分研究[5-6]。离心压缩作为一种新的粉体压缩方式，其压缩效果的影响因素也尚未得到充分研究，并且压坯的密度分布对后续分散有着重要影响。目前常用的实验手段难以获得粉体在压缩过程中的密度变化，现有的能够获得粉体柱详细信息的非入侵式实验方法是通过X射线或γ射线计算机断层扫描，但由于其花费巨大、过程复杂，很少被应用在实验测试中[7]，因此需要借助数值模拟方法对离心压缩过程中的粉体密度变化进行研究。

由于离散元法(discrete element method,DEM)适用对象的离散性与粉体颗粒高度匹配，因此离散单元法已在粉体研究领域得到广泛应用。Gao等[8]应用离散单元法针对药物粉体压缩过程进行了模拟，建立了一种定量关联离散元药物粉体压缩行为的新方法。Thakur等[9]使用离散单元法模拟了粉体在粉体测试仪中的堆积、压缩和结块行为，模拟结果与实验中的压缩与流动特征相吻合。为了研究离散单元法对受限颗粒床压缩过程模拟的准确程度，Persson等[10]进行了颗粒床压缩的实验与数值模拟研究。已有研究结果表明，离散单元法适用于模拟粉体的小变形情况，对大变形情况并不适用[11]。受粉体洗消剂后续分散使用条件的制约，需要对粉体洗消剂进行低压压缩，并不需要其完全致密化，颗粒间更多发生的是微小形变，因此离散单元法适用于对粉体洗消剂的离心压缩过程进行模拟，并且国内外针对颗粒离心压缩的实验、仿真及数据分析的有关研究较少，为促进离心压缩在粉体洗消剂装填及分散过程的高效应用，亟需开展相关方面研究。

1 离散元法基本原理

离散元法作为一种新的数值模拟方法研究对象主要针对非连续介质，最初由Cundall等[12]提出，具体实现过程是根据颗粒间的实际接触情况建立相对应的接触模型。根据颗粒的受力情况和相对位移，计算得到作用于颗粒间的接触力，再由牛顿第二定律获取颗粒的加速度[13]，因此选取合适的模型、参数，可以不断重复上述过程，更新单元的空间信息，实现对颗粒体系实际运动状态的模拟。

由于二氧化硅颗粒与粉体洗消剂的密度、弹性模量相似，便于模拟粉体洗消剂的压缩及后续分散过程，因此本文中选用二氧化硅球形颗粒作为粉体洗消剂的替代研究对象，对其离心压缩过程进行模拟。由于二氧化硅颗粒球形度较高、表面光滑，采用Hertz-Mindlin接触模型描述颗粒间的相互作用。图1为颗粒a(小实线圆)和b(大实线圆)接触时的受力示意图。在外力作用下，颗粒b从原有位置点B运动至颗粒b′(大虚线圆)位置点B′处，在接触点C与C′间会发生微小形变。该模型通过颗粒间的微小重叠量描述颗粒间的相互作用，通过引入弹簧与阻尼器描述颗粒碰撞所引起的接触力和阻尼力。

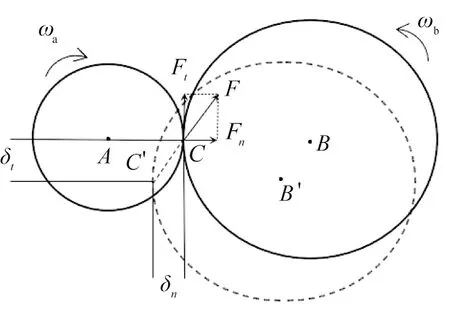
图1 颗粒接触时的受力示意图Fig.1 Force schematic diagram of particles in contact

在Hertz-Mindlin接触模型中，法向力Fn通过法向重叠量δn计算得到，即

(1)

式中：E*、R*分别为等效弹性模量和等效接触半径。切向力Ft则通过引入切向刚度及切向重叠量δt计算：

Ft=-Stδt。

(2)

式中St为切向刚度。

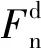
(3)

(4)

其中

(5)

(6)

(7)

(8)

(9)

(10)

(11)

式中：Sn为法向刚度；m*为等效质量；vn为法向速度；vt为切向速度；G*为等效剪切模量；e为颗粒的恢复系数；Ea、va、Ra、Ga、ma和Eb、vb、Rb、Gb、mb分别为颗粒a和颗粒b的杨氏模量、泊松比、半径、剪切模量以及质量。

此外，颗粒在接触过程中还会受到由切向力导致的滚动摩擦，通过引入力矩τ进行描述，即

τ=-μFnRω,

(12)

式中：μ为滚动摩擦系数；R为颗粒半径；ω为颗粒接触处角速度。

2 实验

材料选用粒径为0.4～0.5 mm的二氧化硅球形颗粒。利用电子天平(精度为0.001 g)称取质量为30 g的二氧化硅颗粒置于容器内，再利用玻璃漏斗全部倒入内径为23 mm、高度为95 mm、壁厚为1.5 mm的聚丙烯(PP)平底料筒内，再缓慢提高玻璃漏斗至全部颗粒流入料筒内。使用Hite700型测高仪(瑞士TESA公司，精度为0.000 1 mm)测量料筒内的二氧化硅颗粒堆积高度。将料筒放入非标离心机(实验室自主设计)中，在转速为1 500 r/min的条件下进行离心压缩，60 s后取出，再使用测高仪对离心压缩后的二氧化硅颗粒堆积高度进行测量。由于二氧化硅颗粒的堆积过程具有一定随机性并且离心压缩后颗粒高度并不水平，为减小误差，选取沿径向上2个点进行测量，结果见表1。为获得精密度较好的实验结果，采用Q检验法对实验数据进行检验，结果见表2。

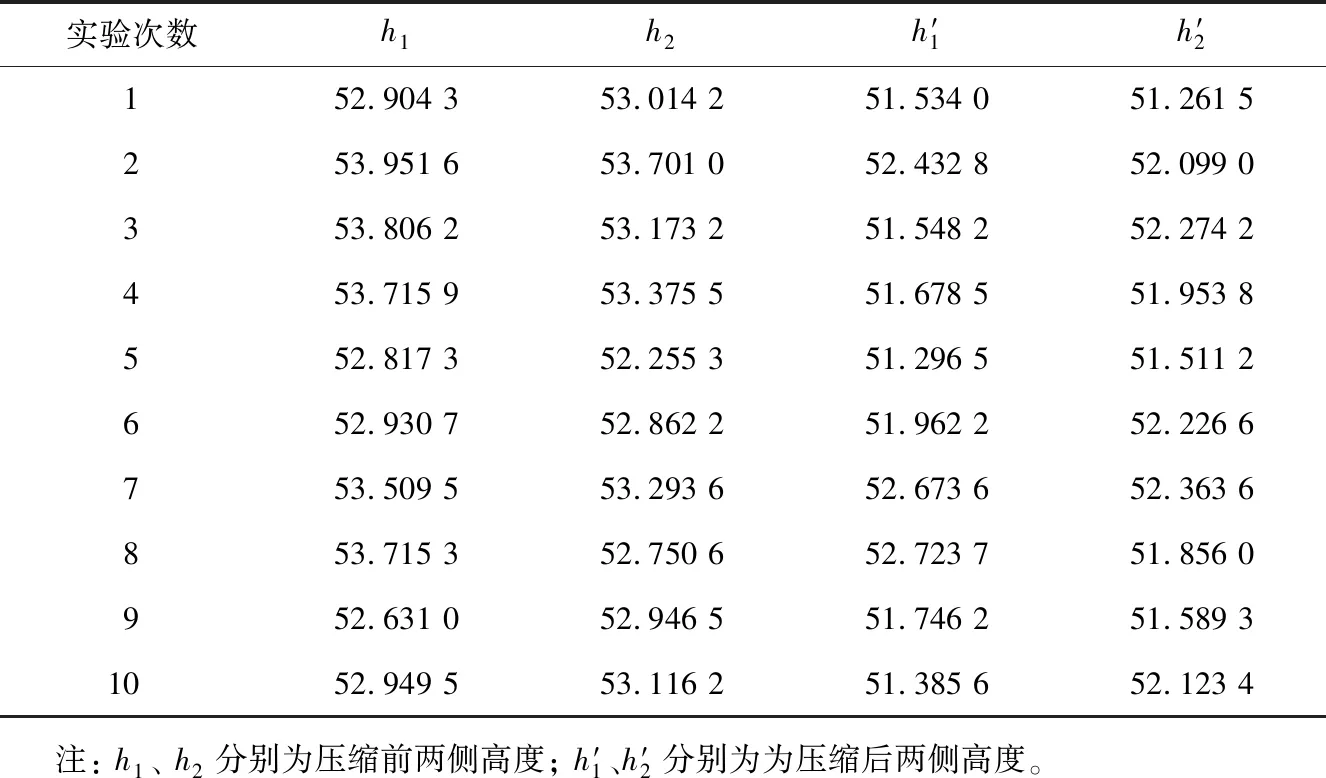
表1 粉体颗粒离心压缩前、后两侧高度的实验测量值Tab..1 Experimental measured values of height of powder particles on both sides before and after centrifugal compression mm

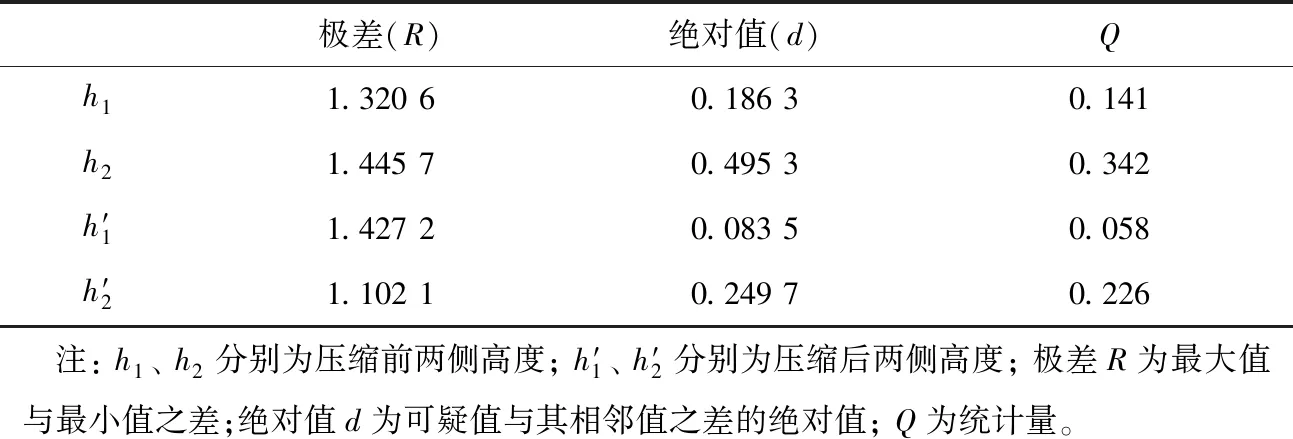
表2 数据检验Tab..2 Data validation with Q-test

通过查Q值表，在置信度为90%、测量10次的情况下，Q=0.41。10组数据的Q值均小于0.41，故无异常值。

3 仿真

3.1 粉体颗粒离心压缩仿真

应用离散元软件仿照实验过程对离心压缩过程进行模拟。为减小计算量，选择对单一粒径的球形颗粒进行模拟，生成粒径为0.45 mm、总质量为30 g的球形颗粒，通过有关文献[14-17]获得仿真所需参数，见表3。

表3 粉体颗粒离心压缩仿真参数设置Tab..3 Setting of simulation parameters for centrifugal compression of powder particles

模拟过程按照离心机实际工作状态分为以下3个阶段。1)阶段I(0～0.1 s)。在内径为13 mm、高为95 mm的料筒内静态生成质量为30 g的颗粒。2)阶段II(0.1～4 s)。料筒从竖直状态旋转至水平状态，开始进行离心压缩。3)阶段III(4～4.8 s)。离心压缩结束，料筒从水平状态旋转至竖直状态。仿真过程如图2所示。

图2 粉体颗粒离心压缩仿真过程Fig.2 Simulation process of centrifugal compression on powder particles

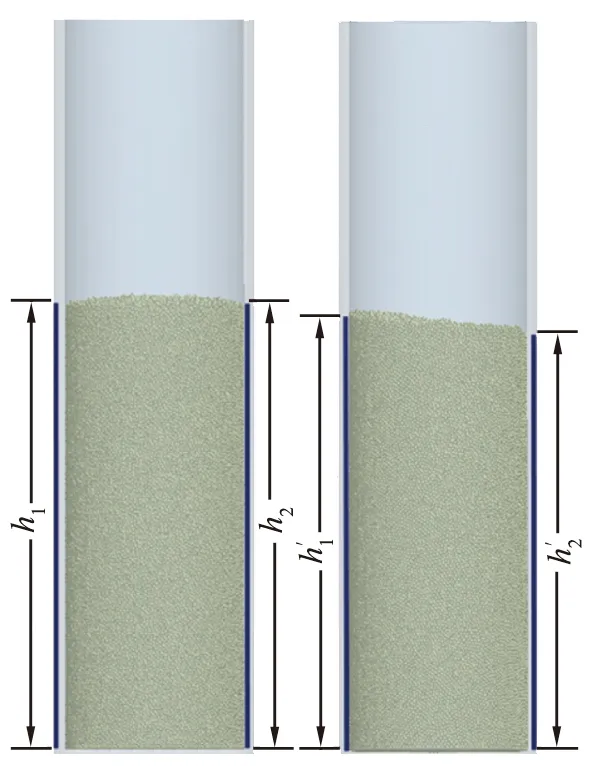
(a)自然堆积 (b)压缩后图3 粒径为0.45 mm的颗粒压缩前、后两侧高度Fig.3 Height on both sides of 0.45 mm particles before and after centrifugal compression

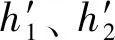
3.2 离心压缩粉体颗粒密度变化

在上述模拟基础上，统计颗粒堆积阶段(0.1 s)、离心压缩阶段(4 s)、压缩结束转至竖直阶段(4.8 s)粉体柱各区域的密度数据，并应用Matlab软件绘制了如图4所示的纵剖面密度分布云图。由于粉体柱上表面并非平整界面，故统计范围选为从料筒底部至粉体柱上表面最低点。

当颗粒堆积完成后，粉体柱有最大高度；随着离心压缩的进行，粉体柱高度不断减小，在压缩刚结束时，高度减至最小，约为50 mm。之后料筒在水平状态变为竖直状态过程中，由于离心力变小，会导致一部分颗粒发生回弹并且在粉体柱上端有小部分颗粒发生滑移现象，类似于图2(b)中的情形，造成粉体柱高度有一定回升，上表面最低点从50 mm回升至52 mm。从密度分布图中可以看出，无论是局部最高密度还是平均密度，均为压缩刚结束时最大(如图4(b)所示)，但即使经竖直操作并短暂放置，粉体发生回弹，其最终密度(如图4(c)所示)仍大幅大于初始密度(如图4(a)所示)。在图4(c)中左上部分密度降低正是由颗粒在从水平状态转至竖直状态时发生滑移所造成的。离心压缩时，在离心力的作用下，颗粒间堆积十分紧密，具有稳定的力链结构，颗粒间相互作用较强，其间产生的摩擦足以对抗颗粒的重力作用，颗粒不发生显著滑移；但随着离心转速逐渐降低，颗粒间相互作用也随离心力减小而减小，部分粉体颗粒在重力作用下产生滑移，原有的稳定力链体系被打破，该部分颗粒重新变为松散状态，导致局部密度减小。

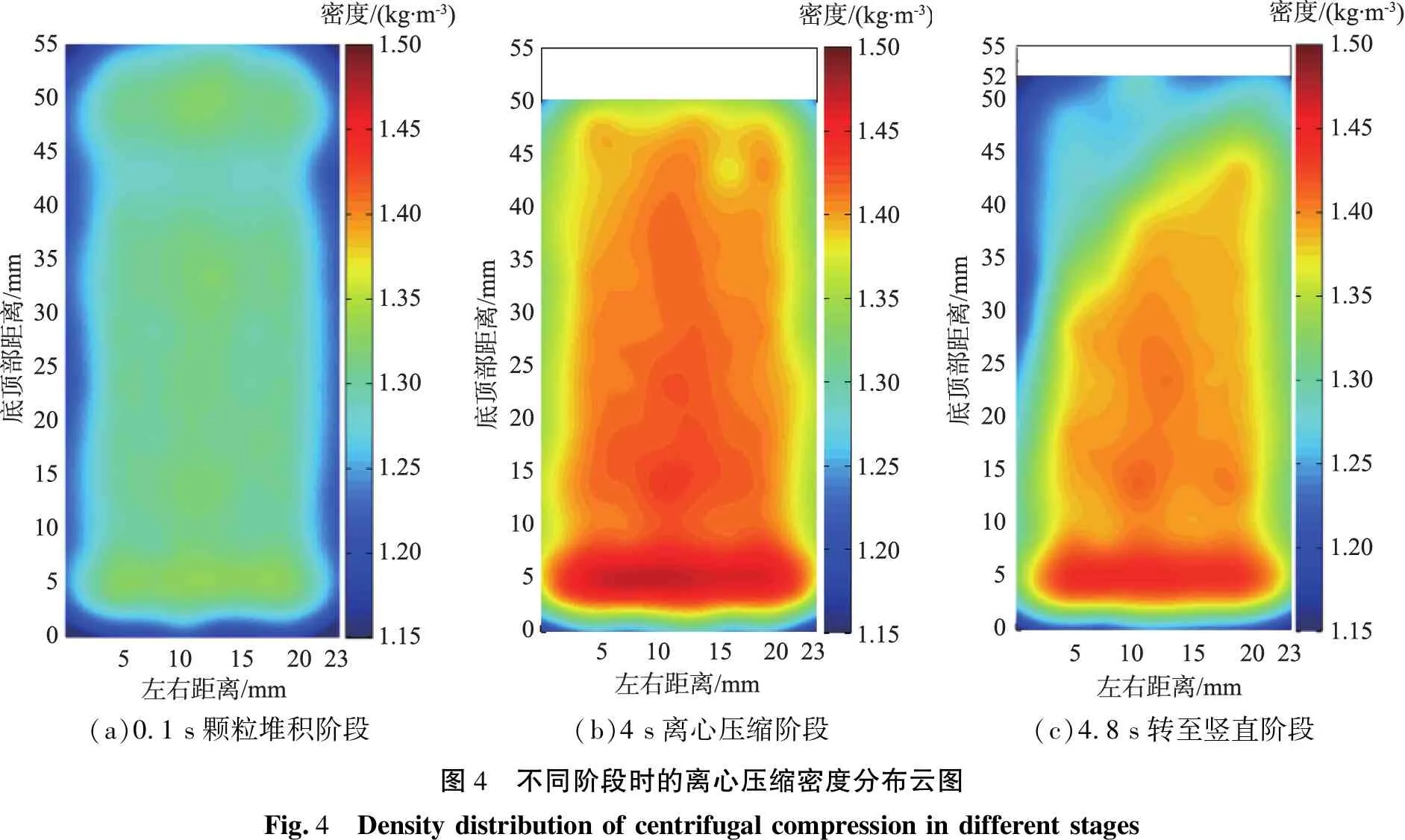
(a)0.1 s颗粒堆积阶段(b)4 s离心压缩阶段(c)4.8 s转至竖直阶段图4 不同阶段时的离心压缩密度分布云图Fig.4 Density distribution of centrifugal compression in different stages

3.3 压缩方式对密度分布的影响

离心压缩与传统的单向高速液压压制相比，主要区别在于主导颗粒压实的力不同。离心压缩是全体颗粒受到离心力作用，其中距离旋转轴心较远的颗粒即容器底部颗粒受力更大；而单向液压压制条件下，颗粒受到由上而下的压力作用，颗粒间成拱效应使得上层的压力可能不能完全传导至下层，导致颗粒上层受力大而下层受力小。受力情况的不同导致颗粒密度分布存在一定区别。

图5(a)为离心压缩结束时的密度分布等高线图。从图中可以看出，压缩后粉体柱的密度分布主要呈现以下规律：1)沿料筒径向密度基本呈现对称分布；2)料筒中部密度分布较为均匀，所占比例较大；3)料筒底部中下位置密度最大，密度呈现向四周逐渐减小趋势并在四角处密度最小。图5(b)为对铁粉进行单向液压压制所得到的密度分布等高线图。文献[18-19]指出其密度分布主要呈现规律如下：

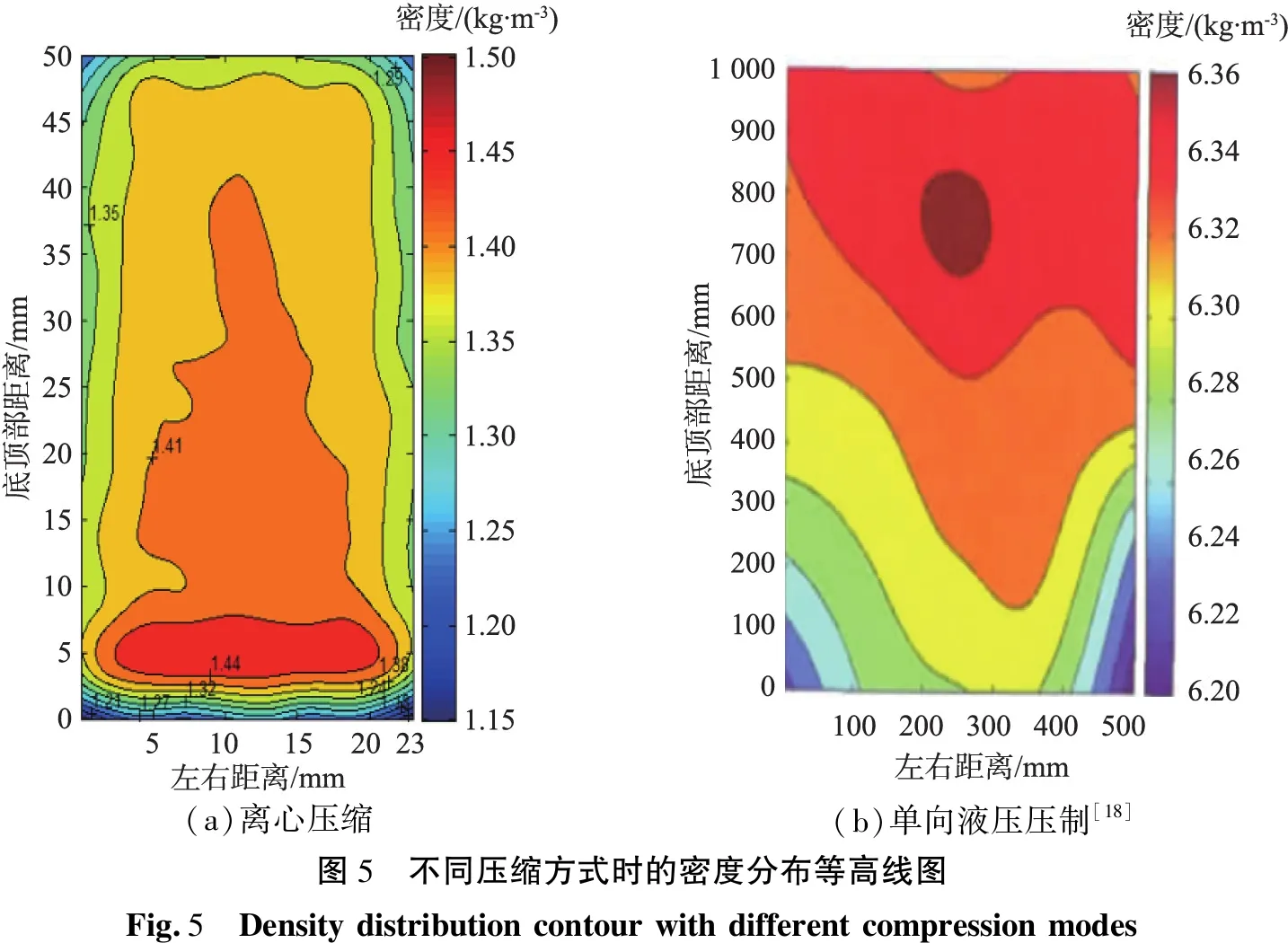
(a)离心压缩(b)单向液压压制[18]图5 不同压缩方式时的密度分布等高线图Fig.5 Density distribution contour with different compression modes

1)从上到下密度减小；2)中上部分密度最大，其他部分次之，下端两角最小；3)左右密度呈对称分布。

与传统的单向液压压制相比，离心压缩的粉体柱密度分布规律具有一定特点，主要体现在密度最大部分主要集中在料筒底部位置，料筒底部以及壁面附近都存在一定的密度梯度，并且料筒中部密度所占比例较大；而单向液压压制密度最大部分主要位于模具的中上位置，轴向密度变化主要体现在压坯底部。

3.4 粒径对密度分布的影响

为了研究颗粒粒径对离心压缩过程中密度分布的影响，选用直径为0.45、0.9 mm的颗粒与混合颗粒(直径为0.45、0.9 mm颗粒的等质量混合，每种颗粒各占混合后颗粒质量的50%)3类球形粉体颗粒进行离心压缩模拟，生成颗粒质量均为30 g，参数设置见表3。对离心压缩结束(4 s)时的密度分布情况进行统计，得到3种颗粒的密度分布见图7。从图中可以看出，压缩后的粉体密度分布规律与之前总结的规律大致相同，但当所模拟的颗粒粒径发生变化时，其密度变化也存在一些明显差异，主要表现在密度分布及密度大小上。

对比图6(a)、(b)可以看出，随着颗粒粒径的减小，粉体柱密度呈现整体增加趋势并且图6(b)中间位置的密度分布相对均匀。分析认为，在体积固定的情况下粒径越小的颗粒越容易发生颗粒间的重排，而离心压缩过程又促进了颗粒间的重排，使得小颗粒更容易填充原有的空隙，导致其密度分布相对均匀，并且压缩后小颗粒间的排布会更加紧密，因此其压缩后的密度也更大。从图6(c)可以看出，压缩后的混合颗粒密度显著增加，不仅中部区域密度值较大而且高密度区域面积也更大。较图6(a)、(b)，图6(c)中的粉体柱在底顶部距离为5～35 mm区域轴向密度变化较小，整体而言密度变化相对均匀，但是其中局部区域间密度存在一定差异。分析认为与混合颗粒体系中大小颗粒的排布方式有关。在混合颗粒体系中，当小颗粒占主导地位时，小颗粒环绕少量大颗粒，形成类似于啮合结构的颗粒聚集体，如图7(a)所示。该类颗粒结构间存在的楔入效应随离心压缩的作用而减弱，趋近于实心材料并具有更大的密度[20]。当大颗粒占主导地位时，小颗粒填充于大颗粒之间，如图7(b)所示，但受尺寸因素影响颗粒之间仍会存在一定间隙，计算可得在固定体积情况下小颗粒占主导地位的颗粒聚集体具有更大的密度。图8所示为粉体柱截面，从图中能够清楚地观察到，在混合颗粒体系中存在许多类似的颗粒结构。该截面中以小颗粒为主的颗粒结构用红圈标出，以大颗粒为主的颗粒结构黑圈标出，还有许多类似结构并未全部标出。

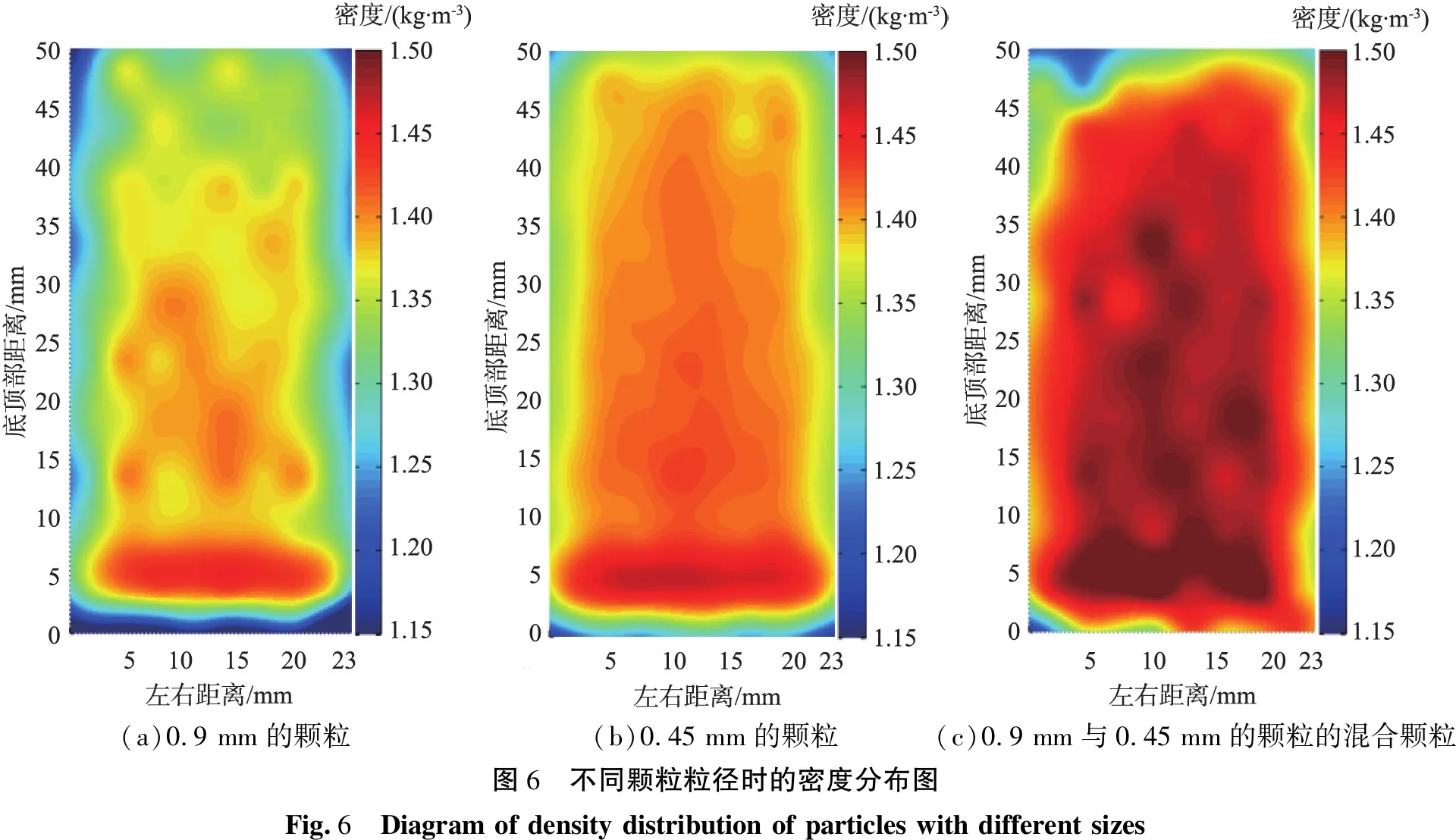
(a)0.9 mm的颗粒(b)0.45 mm的颗粒(c)0.9 mm与0.45 mm的颗粒的混合颗粒图6 不同颗粒粒径时的密度分布图Fig.6 Diagram of density distribution of particles with different sizes

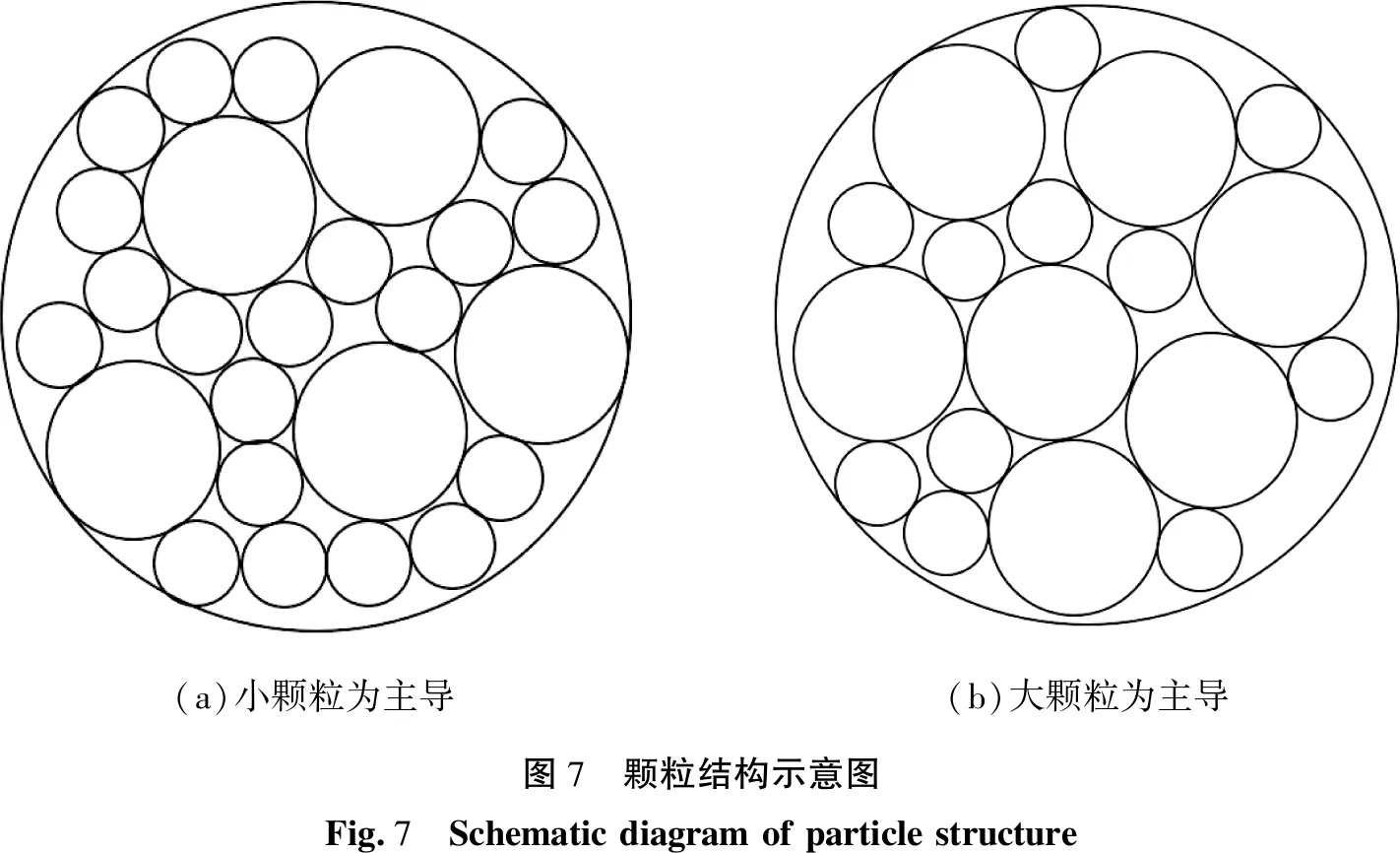
(a)小颗粒为主导(b)大颗粒为主导图7 颗粒结构示意图Fig.7 Schematic diagram of particle structure

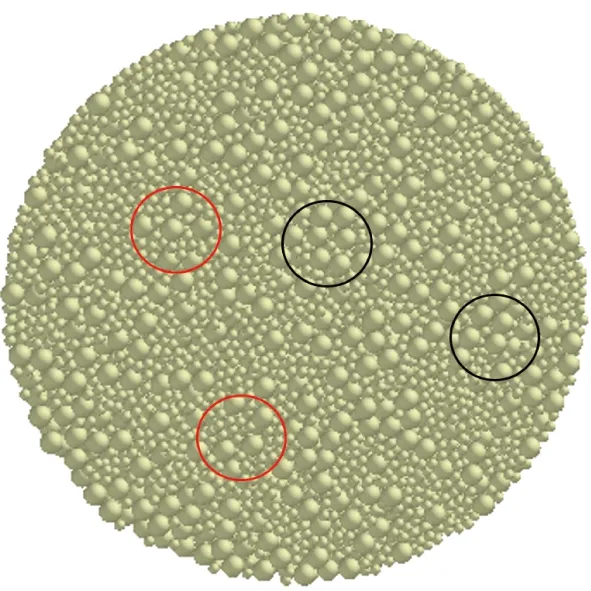
图8 粉体柱截面Fig.8 Section of powder column

通过上述对比发现，在离心压缩实验中，改变颗粒粒径在一定程度上影响压缩后的粉体柱密度及其密度分布。在其他参数不变的情况下，通过减小颗粒粒径使得压缩后的粉体柱密度增大，密度分布均匀。同时，如果适当添加部分小颗粒，不仅可以大幅增大压缩密度，还能使得压缩后的粉体柱密度分布更加均匀，并增大粉体柱内的高密度区域面积。

3.5 粉体层密度随时间的变化

为了进一步分析离心压缩过程中粉体柱各位置的密度变化情况，在料筒内部分别选取2个位置进行密度统计。选取的研究对象为2个直径为23 mm、高度为5 mm的颗粒层。其中心分别位于距离粉体柱底部2.5、17.5 mm处。在模拟过程中，对2个颗粒层的质量进行实时测量，从而得到颗粒生成阶段至离心压缩结束(0～4 s)粉体颗粒层的密度随时间的变化曲线，见图9。其中底部颗粒层密度变化为黑色曲线，中间颗粒层密度变化为红色曲线。从图中可以看出，在离心压缩过程中粉体颗粒密度随时间变化具有明显规律性，即在离心压缩过程中粉体颗粒密度随时间具有先迅速增加，之后趋于固定值的变化趋势。分析认为，在离心压缩开始阶段，粉体颗粒处于自然堆积状态，此时颗粒体系内存在较大空隙。随着料筒开始运动，自然堆积状态下的颗粒稳定体系被打破，颗粒间开始进行重新排列，导致原有的空隙被迅速填充，该阶段为粉体颗粒密度随时间变化而迅速增加的阶段；随着压缩的继续进行，粉体颗粒体系变得密实，当到达一定程度后，粉体颗粒体系内形成新的稳定结构，使得粉体颗粒密度趋于固定值。该现象与粉体压缩过程第一阶段的理论相吻合[21-22]，但由于离心压缩过程为低压压缩，因此并不会导致颗粒发生大的形变。另外，在3条曲线的上升阶段都出现了粉体柱密度突然减小的现象。原因是该现象与离心方式有关，在料筒从竖直状态旋转至水平状态过程中，料筒内粉体颗粒产生如图2(b)所示的滑移现象，导致粉体堆积变得松散，密度突然减小。

从数值方面，对图9中的曲线进一步分析可以发现，颗粒按密度从大到小排列的次序为混合颗粒、直径为0.45 mm的颗粒、直径为0.9 mm的颗粒。该现象与Yohannes等[23]的结论相符。同时，在经过离心压缩后，料筒底部颗粒层与料筒中部颗粒层存在一定密度梯度，该梯度在图9(a)、(b)中较为明显，且二者差距不大，但在图9(c)中该梯度并不明显，即混合颗粒密度梯度小于单一颗粒密度梯度。这也从数值方面证明了相比于单一粒径，混合颗粒底部与中部颗粒层密度梯度更小，密度分布更加均匀。

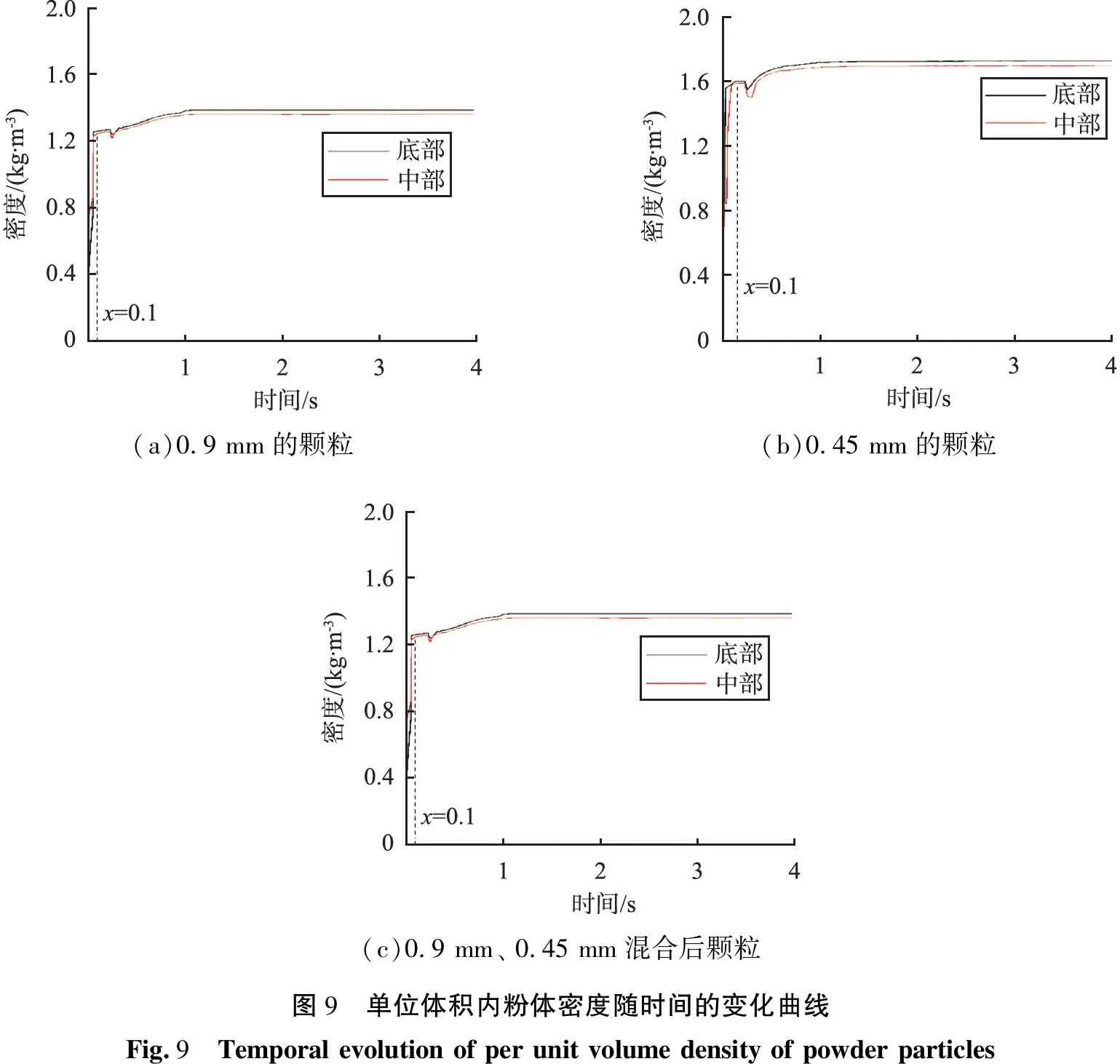
(a)0.9 mm的颗粒(b)0.45 mm的颗粒(c)0.9 mm、 0.45 mm混合后颗粒图9 单位体积内粉体密度随时间的变化曲线Fig.9 Temporal evolution of per unit volume density of powder particles

4 结论

1)基于离散元法的粉体颗粒离心压缩仿真与实验测试结果误差不大于5.82%，证明在合适的接触模型和参数设置情况下，采用该方法进行数值模拟合理、可靠，能够为难以通过实验测得的粉体柱密度及分布提供一种解决方法。

2)不同压缩方式作用下粉体柱密度分布存在明显不同。离心压缩后粉体密度沿料筒轴向呈现对称分布，料筒中部密度分布相对均匀且所占区域较大，料筒底部中下位置密度最大，密度总体呈现向四周减小的趋势。

3)在离心压缩中，减小颗粒粒径有利于增大粉体柱密度，并使其分布更加均匀。适当添加部分小颗粒，可以大幅增大压缩后粉体柱密度及均匀性。

4)离心产生的单位体积粉体密度随压缩时间和转速先迅速增大，之后趋于固定值。仿真数据解释了随着转速增大，粉体颗粒经历了稳定体系重建直至最终稳定的过程。随着离心转速逐渐增大，料筒发生了垂直—水平—垂直运动方式的改变，顶部表面颗粒出现部分滑移。

通过对粉体颗粒离心压缩的过程特征进行分析，得出的以上结论为洗消弹内粉体分散所需气流力、气流导入方向及结构等研究提供了技术支撑。