一种基于高斯混合模型的不均衡分类方法
方佳锴


摘要:为应对不均衡分类问题,提高分类准确率,提出了一种基于高斯混合模型的混合采样集成方法GMHSE(Gaussian-Mixture-model-based Hybrid Sampling Ensemble method),首先通过高斯混合模型将数据划分成多个类簇,然后在每个类簇上混合采样获得多个数据子集,最后基于Bagging技术在类簇内和类簇间进行加权投票完成分类预测。GMHSE通过聚类将对数据进行划分,混合采样保障在不丢失数据信息的同时获得均衡数据集,最后利用集成学习进一步提升模型的泛化性能。实验结果表明,相比已有的一些处理方法,GMHSE可以提升不均衡数据的分类性能。
关键词: 不均衡分类; 高斯混合模型;集成学习;混合采样
中图分类号:TP3 文献标识码:A
文章编号:1009-3044(2022)02-0028-03
1 概述
在数据挖掘的许多应用,例如医疗诊断[1]、欺诈识别[2]等,都存在着类别不均衡问题。当数据集中来自不同类的实例数量差距较大时,则该数据集存在类别不均衡问题,会限制学习算法的泛化能力,影响分类性能。
目前已经提出了一些技术来克服这些问题,这些技术可以分为采样方法、代价敏感学习和集成学习。采样方法在通过对数据集进行预处理实现类别均衡,典型的算法有随机欠采样方法和随机过采样。代价敏感学习[3]通过对少数类样本的误分类赋予较大的代价,使分类器更重视少数类样本的训练,从而降低整体分类误差。集成学习方法结合多个基础学习器,可以显著分类准确性。将集成学习方法与采样方法相结合,可以有效处理不均衡分类问题[4],典型算法包括RUSBoost[5]、SMOTEBagging[6]等。这类方法一般通过某种采样方法生成一系列子数据集,再用集成学习方法对新实例进行预测。然而单种采样方法具有局限性,欠采样会删除多数类样本数据导致巨大的信息损失,过采样会使模型有过拟合风险。此外,目前的方法直接对整个数据集进行采样,没有在数据空间上做更细致的划分,这也限制了模型的分类准确性。
本文针对不均衡分类问题提出了一种基于高斯混合模型的混合采样集成方法GMHSE(Gaussian-Mixture-model-based Hybrid Sampling Ensemble method)。首先,高斯混合模型将数据划分到不同类簇。接着,根据类簇内的类别不均衡比例进行混合采样。在每个类簇上采样得到的数据能更全面地代表原始数据的信息,混合采样方法则避免了单种采样方法的弊端。最后,基于Bagging方法在类簇内和类簇间进行加权投票,获得最终的预测值。本篇文章的主要工作可以总结为:(1)文章提出了一种新的应对不均衡分类问题的算法GMHSE;(2)在8个公开数据集上进行了实验,结果表明GMHSE相比其他方法表现更好。
后续文章的组织结构如下:第2节详细介绍了GMHSE算法模型,第3节介绍实验设置及结果分析,第4节为结论部分。
2 算法模型
2.1 高斯混合模型
高斯混合模型(Gaussian Mixture Model,GMM)模型是多个多元高斯混合分布函数的线性组合[7],定义为Pr(x)= ∑πk N(x; uk和θk),一共有K个高斯分布,uk和θk为第k个高斯分量的参数,πk是该高斯混合分量的权重因子。理论上GMM 可以拟合出任意类型的分布。
采用GMM对训练集(包括多數类实例和少数类实例)进行拟合,其类簇数量K可以根据贝叶斯信息准则(Bayesian information criteria,BIC)[8]选择。BIC = kln(n)+2ln(L),其中k为模型参数个数,n为样本数量,L为似然函数,该公式引入的惩罚项考虑了样本数量,样本数量过多时,可有效防止模型复杂度过高。BIC值越低,模型对数据的拟合越好。
用一个含有K个高斯分量的GMM模型对单个实例进行预测时,可以得到一个K维向量v=( p1, p2, ..., pK),pk代表该实例属于第k个高斯分量(即第k个类簇)的概率值。因此GMM模型可以获得实例属于各个类簇的概率值,相比于k-means等算法只能获取所属类簇标签,GMM模型可以获得实例在类簇上的更多信息。
2.2 类簇内混合采样
多数类实例与少数类实例的数量之比称为不均衡比例(imbalance ratio, IR)。在完成聚类后,根据SMOTE算法[9]合成一定数量的少数类实例,使类簇下的IR达到指定的阈值。本文中将阈值IRthreshold设置为9。先聚类再进行过采样,实例的相似度更高,更有利于基于KNN算法合成新实例。此外,由于原有的少数类实例都属于同一类簇,可以确保合成的新实例仍落在类簇内,即仍落在学习算法的决策边界之内,因此生成的少数类实例具有较好的可靠性。
不同于直接在整个训练集上做欠采样,GMHSE对类簇内的多数类实例进行有放回欠采样,采样将迭代N次。采样后的数据集与类簇内的少数类实例数据拼接,形成多个类别均衡的数据子集,其IR不超过R:1。本文中N和R都设置为5。最后用基础学习器F拟合数据子集。基于Bagging思路进行欠采样,可以充分利用尽可能多的多数类实例,在实现类别均衡的同时避免欠采样导致的数据损失。
2.3 新实例预测
新实例x的预测结合了GMM的类簇预测和集成学习的有权投票,一共包括三个步骤。
1) 预测所属类簇。实例经过GMM模型预测可以得到一个K维向量v=( p1, p2, ..., pK),pk代表该实例属于第k个类簇的概率值。
2) 获取类簇上的预测值。在每个类簇上经过混合采样形成了多个数据子集,以及相应的一组基学习器。根据学习器的正确率计算权重: weightki = |Dki0’| / |Dk0| + |Dki1’| / |Dk1|,其中weightki表示第k个类簇第i个学习器的权重,|Dk0|和|Dk1|分别表示第k个类簇上多数类和少数类实例的数量,|Dki0’|和|Dki1’|则表示被学习器正确预测的多数类实例和少数类实例数量。在该式子中,根据实例数量赋予了不同类别不同的权值,从而影响基学习器的权重值。新实例在该类簇上各个基学习器获得预测值,在相应类别添加基学习器的权重。
3) 类簇间投票获取最终预测值。新实例在各个类簇上获得相应预测值后,根据第1)步中的概率向量,以pk作为权重对各个预测值进行累加,权重值较大的类别为最终预测值,即y = argmax(∑ pkwk0, ∑ pkwk1),wkc为该实例在第k个类簇上类别c的累计权重,c为0(多数类)或1(少数类)。
3 实验
3.1 数据集
为了验证上述算法的有效性,本节在8个不均衡公开数据集[10]上进行了对比实验证。数据集详细信息如表1所示。
3.2 评估指标
在本实验中,主要依据F1值和AUC值两个指标衡量算法性能。对于二分类问题,将少数类看作正例,多数类看作负例。Recall为召回率,表示实际为正例且预测为正例的样本数量在所有正例样本中的占比;Precision为精准率表示实际为正例且预测为正例的样本数量在所有预测为正例的样本中的占比,二者基于表2所示的混淆矩阵计算得到。F1值是召回率和精准率的调和平均,适用于不均衡分类问题的评估。AUC(Area Under Curve)是ROC曲线(Receiver Operating Characteristic)和横坐标轴之间的面积,值域为[0,1],数值越大表示模型表现越好。
Recall = TP / (TP + FN)
Precision = TP / (TP + FP)
F1 = 2 * Recall * Precision / (Recall + Precision)
3.3 實验结果
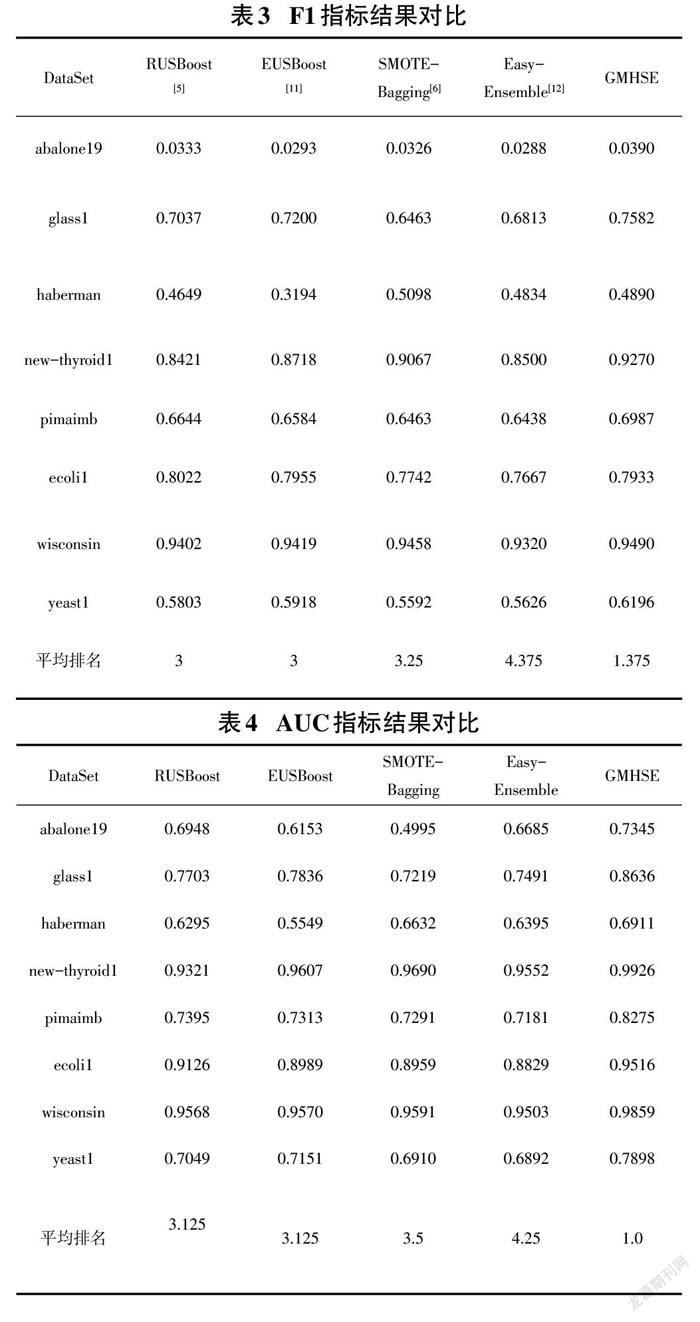
实验中所有算法的基学习器均为C4.5决策树。在每个数据集采用五折交叉验证求得最终评估指标。实验结果如表3和表4所示,最优结果已经加粗表示。本文提出的GMHSE模型,F1指标下在6个数据集中取得最优、在所有数据集平均排名为1.375,在AUC指标下相较于其他算法均有大幅度提升、在8个数据集中均取得最优。由于GMHSE在高斯混合模型聚类的基础上,在每个类簇合了欠采样和过采样构造数据子集,在合成更可靠的少数类实例、解决类别不均衡的同时尽可能避免了多数类实例的信息损失,因此在最终集成预测时能取得更好的结果。
4 结论
本文针对不均衡分类问题,提出了一种新型的基于高斯混合模型的混合采样集成方法GMHSE,首先基于高斯混合模型将数据集分成多个类簇,然后在类簇上进行混合采样得到多个数据子集,再结合集成学习方法进一步增强模型的泛化能力,通过类簇内和类簇间的加权投票获得最终的预测结果。在8个公开数据集上的实验表明,GMHSE在AUC、F1两个指标下相较于已有的方法均取得了最好的分类性能。
参考文献:
[1] He Y Y,Zhou J H,Lin Y P,et al.A class imbalance-aware Relief algorithm for the classification of tumors using microarray gene expression data[J].Computational Biology and Chemistry,2019,80:121-127.
[2] Moepya S O,Akhoury S S,Nelwamondo F V.Applying cost-sensitive classification for financial fraud detection under high class-imbalance[J].2014 IEEE International Conference on Data Mining Workshop,2014:183-192.
[3] JM Yang,C Gao,ZY Qu,et al. Improved Cost-sensitive Random Forest for Imbalanced Classification[J].电脑学刊, 2019,30(2):213-223.
[4] Galar M. A Review on Ensembles for the Class Imbalance Problem: Bagging-, Boosting-, and Hybrid-Based Approaches[J]. IEEE Transactions on Systems Man & Cybernetics Part C Applications & Reviews, 2012, 42(4): 463–484.
[5] Seiffert C, Khoshgoftaar T M, Hulse J V, et al. RUSBoost: Improving classification performance when training data is skewed[C]//International Conference on Pattern Recognition, 2008:1-4.
[6] Zhang Y Q,Zhu M,Zhang D L,et al.Improved SMOTEBagging and its application in imbalanced data classification[C]//IEEE Conference Anthology.January 1-8,2013,China.IEEE,2013:1-5.
[7] Wang Z F, Zarader J L, Argentieri S. Gaussian Mixture Models[C]// 2019 IEEE Symposium Series on Computational Intelligence (SSCI), 2019.
[8] Celeux G,Soromenho G.An entropy criterion for assessing the number of clusters in a mixture model[J].Journal of Classification,1996,13(2):195-212.
[9] Maciejewski T,Stefanowski J.Local neighbourhood extension of SMOTE for mining imbalanced data[C]//2011 IEEE Symposium on Computational Intelligence and Data Mining.April 11-15,2011,Paris,France.IEEE,2011:104-111.
[10] Alcalá-Fdez J,Fernández A,Luengo J,et al.KEEL data-mining software tool:data set repository,integration of algorithms and experimental analysis framework[J].Journal of Multiple-Valued Logic and Soft Computing,2011,17(2/3):255-287.
[11] Galar M,Fernández A,Barrenechea E,et al.EUSBoost:Enhancing ensembles for highly imbalanced data-sets by evolutionary undersampling[J].Pattern Recognition,2013,46(12):3460-3471.
[12] 秦雅娟,林小榕,张宏科.基于EasyEnsemble算法和SMOTE算法的不均衡数据分类方法:CN108596199A[P].2018-09-28.
【通联编辑:光文玲】
2317501186219

