冲突约束下老旧小区公共空间改造群决策研究
赵璐 李杨









摘 要:老旧小区公共空间改造不仅面临改造空间有限、改造难度大等问题,也面临决策主体更加多元化、改造方式更加市场化的挑战,导致改造工作难以顺利开展、社区矛盾频频产生。基于模糊偏好信息得到冲突最小约束下的老旧小区公共空间改造决策流程,通过修正偏好矩阵,改变决策主体权重,从而消解老旧小区公共空间改造冲突。
关键词:老旧小区;群决策;冲突消解
中图分类号:TU984.12 文献标志码:A 文章编号:1673-291X(2022)02-0044-05
近年来,各地市积极响应国家政策导向,通过购买公共服务的市场化改造方式推进老旧小区改造工作。随着参与老旧小区公共空间改造的决策主体越来越多,且每个决策主体的偏好在不断发生变化,当利益主体互相博弈时,由于缺乏更为科学合理的决策方法和模型,容易出现意见难以一致、决策效率不高等问题,导致冲突不断。因此,有必要建立一个能够消解冲突的老旧小区公共空间改造决策模型。
一、理论基础
老旧小区公共空间改造作为民生工程,终极目的是要反映小区业主的心声和利益[1]。公众参与决策旨在追求一定的经济效益,但需要在满足“必要条件”下最大限度减少运作“成本”,使决策协商程序成为一个各方都乐于去采纳和接受的制度机制[2]。群体决策指两个以上决策主体进行博弈,最终获得共同认可的决策方案的过程[3]。心理学等相关学科的研究结果显示,群体决策质量高于个体单个决策质量[4],也更便于决策结果的落实[5]。
在决策方法方面,可以采用Kemeny局部优化算法制定群决策方案,反映多方不同利益群体的意见和建议[6];也可以在排序或分级的结果上进行优化[7];还可通过波达计数法[8]、模糊多数方法[9]将个体的偏好集结,形成群体偏好决策方案。这些研究虽然考虑了决策成员偏好冲突程度并对选择方案进行优化,但还缺少冲突约束下的老旧小区改造决策进行研究。
二、模型建立
首先基于模糊偏好信息进行老旧小区改造决策主体的聚类,并测量其权重,得到冲突最小约束下的改造决策流程(见图1)。
(一)建立老旧小区公共空间改造群决策偏好矩阵
假设每一老旧小区公共空间改造共有M(M≥20)个决策主体,并针对P个改造方案给出自己的评价矩阵,矩阵Am表示决策者m给出的模糊偏好矩阵,其中aijm表示该决策者认为方案i优于方案j的程度。
1.不完全偏好矩阵缺失值估计
为形成对称性的模糊偏好关系矩阵,可参考应急决策[10]中的计算方式,采用以下公式对不完全的信息进行估计:
xijs=ail+alj-0.5
2.决策主体偏好一致性检验
为了保证参与决策的业主提供的偏好信息可信度更高,需要在聚类之前进行偏好一致性检验,当阙值ρ0=0.8时可得到90%的置信水平[10]。一致性水平ρm计算公式如下:
(二)老旧小区公共空间改造决策群体聚类
为了尽快完成决策工作,应先对业主进行降维处理,分成聚类,进而使得全部决策主体意见达到一致。
1.决策主体偏好关系矩阵相似度测算
本文采用矩阵间相似度测量方法,决策主体m1和m2偏好关系矩阵之间的相似度可表示为:
2.基于冲突最小的阙值设定
为了消解老旧小区公共空间改造决策中的冲突,应以群体共识即矩阵间相似度最大为目标设定阙值,再根据相似度运用SPSS软件绘制决策主体聚类谱系图,即可获得对应的聚集个数。
(三)基于距离熵的决策主体权重确定
可运用熵权法测定决策主体的权重向量,熵值越大则权重越大。聚集的偏好冲突可通过聚类内每个决策主体的冲突水平进行测度,表示为:
再进行归一化处理,可得到决策主体i的熵值[13]:
θi=-γi / ln(nk)
再对熵值进行归一化处理,便得到主体i的权重:
考虑决策会出现“少数服从多数”的现象,综合聚类内决策主体数量因素,重新定义决策主体权重为:
聚类内决策主体权重重新表示为:
ωk=ψω0k+(1-ψ)ω0k
若看重聚类内主体人数对决策结果的影响,可使ψ∈[0,0.5];若更看重距离熵法,可使得ψ∈[0.5,1]。
最终通过Si=aijg公式为改造方案排序,方案排序靠前,冲突度越小,方案越令决策主体满意。
若测量的冲突度大于设定的阙值,则需通过多轮的协商反馈、偏好修正、冲突再测度,直至冲突度小于阙值,最终达到群体共识、冲突消解的目的。
三、案例分析
假设针对西安市J小区公共空间改造有4个决策备选方案,即O=(o1,o2,o3,o4),召集政府部门、施工方、业主代表组成了一个群决策团体,共计20名决策主体,即p=(p1,p2,…,p20)。每个决策主体对4个决策备选方案进行两两比较,形成决策偏好矩阵。
(一)偏好信息矩阵缺失值估计
第一种是对称位置只有一个元素,缺失一个元素:φ532=1-a523=1-0.3=0.7。
第二種是对称位置两个元素均缺失,例:
φ212=((a213+a232-0.5)+(a214+a242-0.5))=0.4,
φ221=1-φ212=0.6
同理可得,φ1214=0.3;φ1241=0.7;φ1412=0.7;φ1421=0.3;
φ1634=0.2;φ1643=0.8。
(二)偏好信息矩阵一致性检验
由于p为老旧小区公共空间改造方案的数目、也是矩阵的最大行列值,将p=4代入可化简为:
以P1决策主体为例,
aij1-(aik1+akj1-0.5)丨=0.5 0.6 0.8 0.70.4 0 0.3 0.40.2 0.3 0 0.30.3 0 0.3 0丨 aij1-(ai11+a1j1-0.5)丨=(0.9 0.9 1.4 1.4)
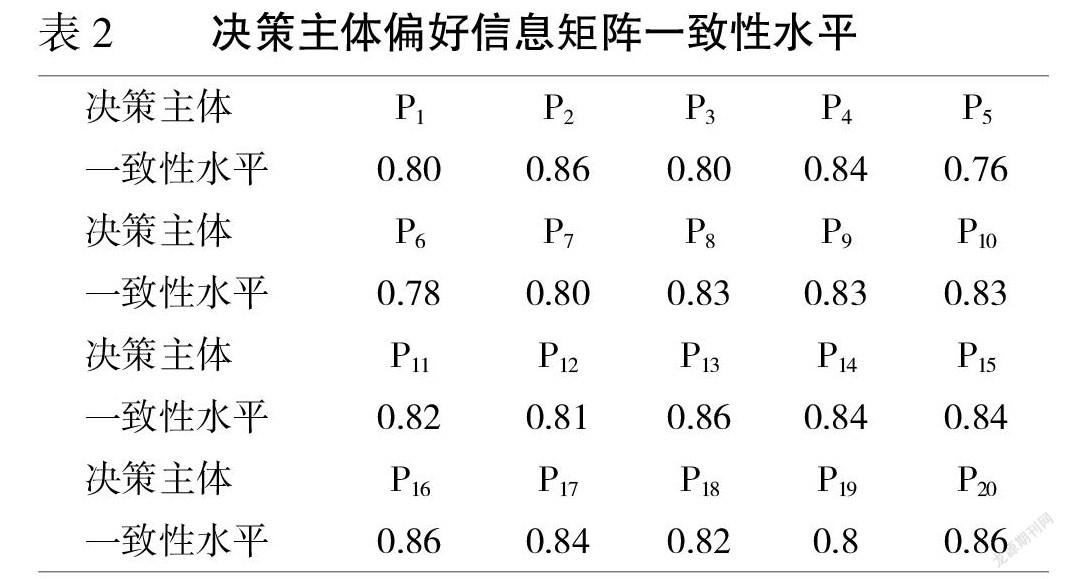
同理可得20位决策主体的偏好信息矩阵一致性水平如表2。
由表2可知,P5、P6一致性水平低于设定好的阙值,需要对其偏好矩阵进行调整。具体修正结果为,将a514=0.1改为a514=0.4,将a541=0.9改为a541=0.6,将a612=0.7改为a612=0.4,将a621=0.3改为a621=0.6。
(三)决策主体偏好关系矩阵相似度测算
将各决策主体偏好矩阵之间的相似度导入SPSS,结果如图3所示。
基于对聚类个数的考量,选取组内平均距离为5,可得到4个组,具体聚类结果如表3。
(四)决策主体聚类内及聚类间权重测算
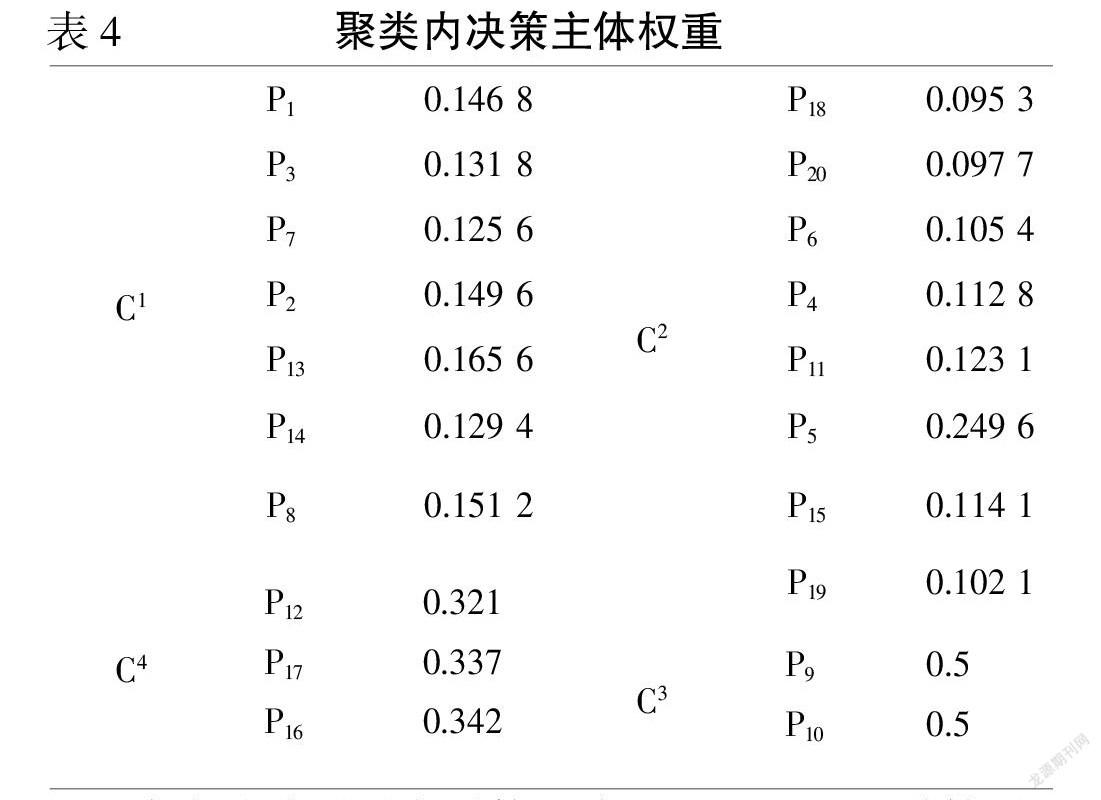
根据聚类内决策主体权重确定模型,得到各聚类内决策主体权重如表4。
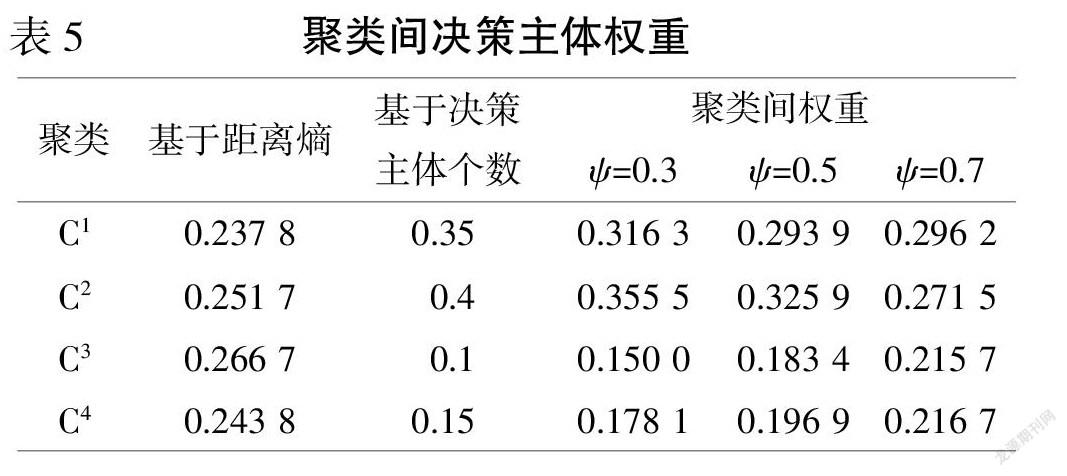
本文选取了可变系数ψ为0.3、0.5、0.7三种情况,得到各聚类间决策主体权重如表5。
(五)决策方案排序
本文选取可变系数为0.7时的方案排序。
由表6可以看出,群偏好矩阵得到的最优方案是方案2。
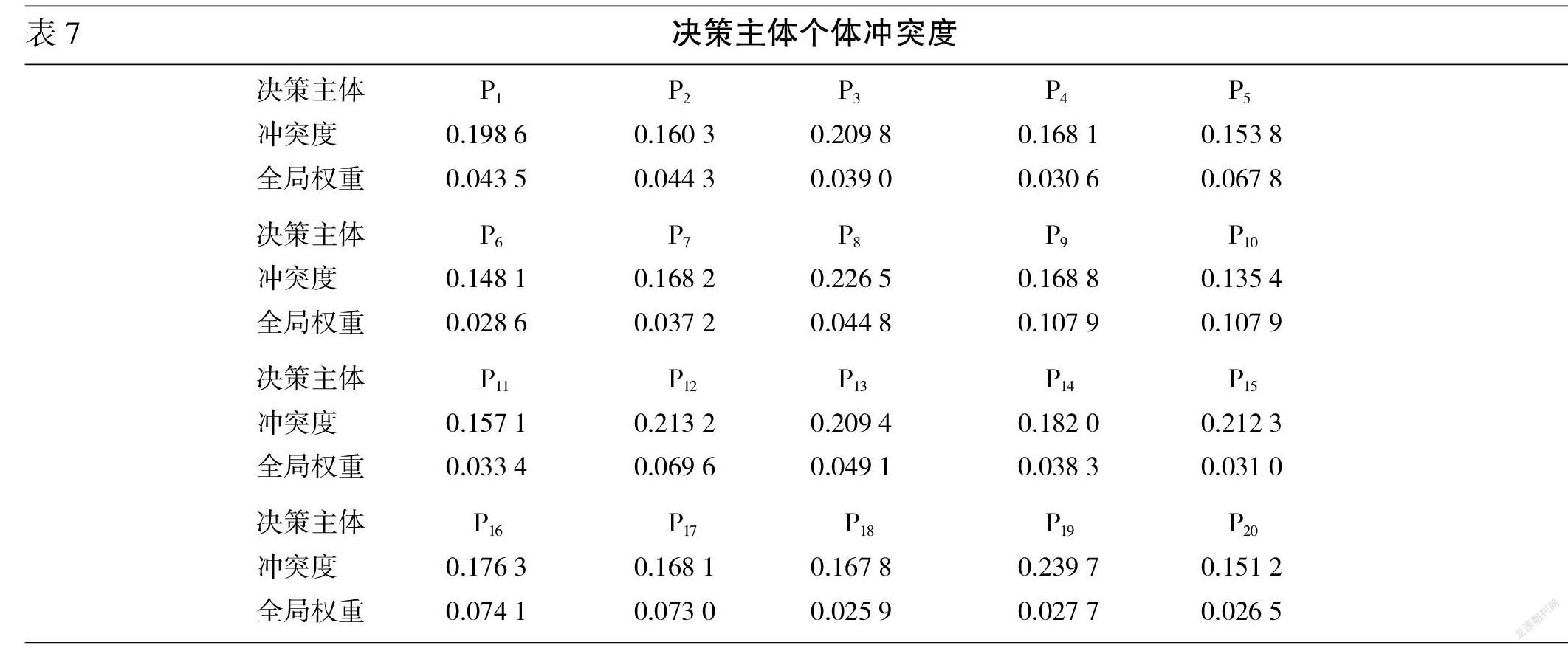
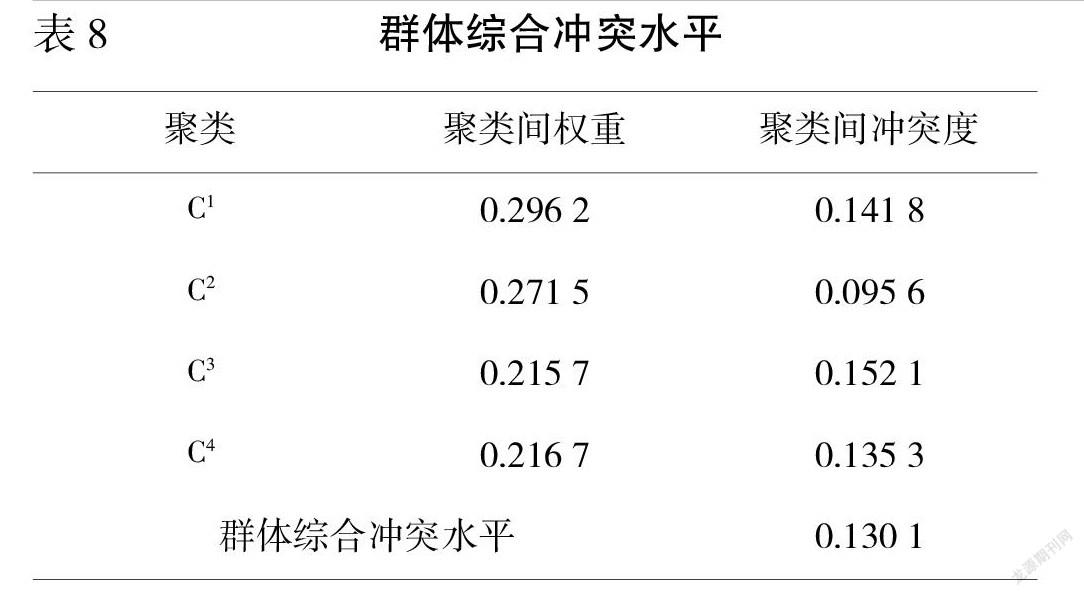
为实现冲突约束下的决策,需要对决策主体的个体冲突度以及聚类间冲突进行测算,并对其进行判定。决策主体的个体冲突度、全局权重以及聚类间冲突度测算结果如下列图表。
根据现阶段群体综合冲突度、决策备选方案数量以及参与决策的决策者数量等等因素,本文设定群体综合冲突水平阈值为0.12。由表8可知,现阶段群体综合冲突水平为0.130 1,大于阙值,需选择修改决策者权重的方式修正偏好,进行冲突消解。
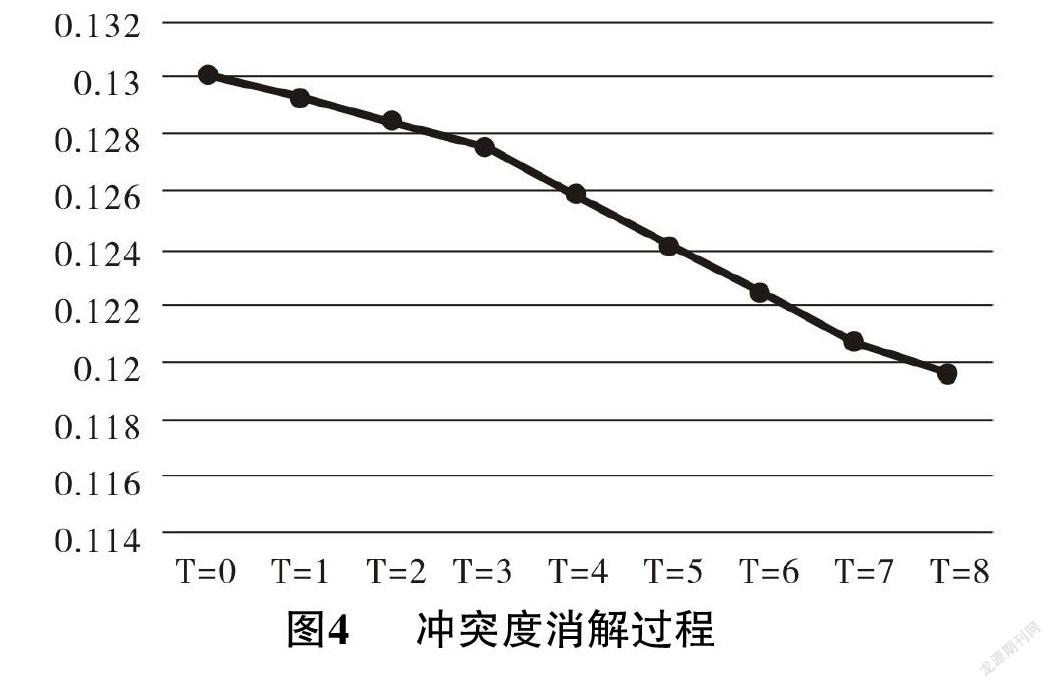
根据8次修正后的综合矩阵冲突度绘制图4,能看到通过协商改变决策主体的权重,可以有效消解老旧小区公共空间改造决策过程中的冲突,实现冲突度的快速收敛,使得群综合信息矩阵的冲突度小于冲突度阙值。
结语
本文将老旧小区改造主体偏好信息不完全、改造方案多样、主体间目标不同等特点融入改造决策的研究中,通过在项目改造决策阶段引入协商理论,根据协商反馈结果修正偏好,降低冲突度较大的决策主体权重,达到消除老旧小区改造过程中多主体间冲突的效果。本文从新的视角进行老旧小区改造决策流程研究,以提高公共决策效率与质量。同时,在确定冲突约束下的老旧小区公共空间改造决策方法的基础上,选取西安市J小区进行案例分析,通过计算20位决策主体对于4个方案的决策结果及权重的更改,验证本文提出的决策方法对于冲突消解的有效性。
参考文献:
[1] 杨帆,王晓鸣,陈亮.基于复杂适应系統的旧城改造利益共生参与机制[J].华中科技大学学报:城市科学版,2005,(3):40-43.
[2] 吴明熠.从听证走向协商:公众参与行政决策的实践反思与程序嬗变[J].甘肃行政学院学报,2020,(2):46-61,125-126.
[3] 池丽萍,辛自强,孙冬青.群体决策质量评估方法及其在大学生和社区居民中的应用[J].心理科学进展,2020,28(1):41-54.
[4] 卢志平.群体决策过程的复杂性及其演化[J].科技管理研究,2010,30(14):264-268.
[5] 陈明榴.群体决策综述[J].科教导刊:电子版,2015,(1):187.
[6] 陶海燕,周淑丽,卓莉.城中村有序改造的群决策——以广州市城中村改造为例[J].地理研究,2014,33(7):1207-1216.
[7] Lee S,Seo K K.A Hybrid Multi-Criteria Decision-Making Model for a Cloud Service Selection Problem Using BSC,Fuzzy Delphi Method and Fuzzy AHP[M].2016.
[8] Zarghami M. Soft computing of the Borda count by fuzzy linguistic quantifiers[J].Applied Soft Computing,2011,11:1067-1073.
[9] Boroushaki S,Malczewski J.Using the fuzzy majority approach for GIS-based multicriteria group decision-making[J].Computers & Geosciences,2010,(36):302-312.
[10] Urena R,Chiclana F,Fujita H,et al. Confidence-consistency driven group decision making approach with incomplete reciprocal intuitionistic preference relations[J].Knowledge-Based Systems,2015,89(NOV.):86-96.
Research on Multi-objective Integrated Management of Old Residential Districts under the Concept of Co-construction, Co-governance and Sharing
ZHAO Lu, LI Yang
(Xi'an University of Architecture and Technology, Xi'an 710055, China)
Abstract: The transformation of public space in old communities not only faces problems such as limited space for transformation and difficulty in transformation, but also faces the challenges of more diversified decision-making bodies and more market-oriented transformation methods, the renovation work is difficult to carry out smoothly, and community conflicts frequently arise. Based on fuzzy preference information, this paper obtains the decision-making process of public space reconstruction of old communities under the constraint of minimum conflict. By modifying the preference matrix, the weight of decision-making subjects is changed, and then the conflicts of public space reconstruction of old communities are resolved.
Key words: old community; group decision-making; conflict resolution
[責任编辑 张宇霞]
3059501908239

