脉冲双星加速度搜索方法及软件改进 *
冀昶旭,于徐红,刘志杰
(贵州师范大学贵州省信息与计算科学重点实验室,贵州 贵阳 550001)
脉冲双星系统的发现极具科学意义。1974年,赫尔斯和泰勒在天鹰座天域探测到脉冲信号,经计算发现是脉冲双星[1](PSR B1913 + 16)的信号。两人通过深入研究首次发现引力波存在的间接定量证据[2],并因此获得1993年诺贝尔物理学奖。文[3]基于500 m口径球面射电望远镜数据在M13星团中发现一颗处于双星系统中的毫秒脉冲星M13F,并认证星团中另一颗脉冲星M13E为掩食双星;首次测量了M13星团中4个脉冲双星系统的轨道椭率,同时获得M13星团现有脉冲星的最好计时结果。遗憾的是,现有脉冲双星的搜索较为耗时,搜索能力亟待提升。一方面是FAST早期科学数据中心对数据存储和处理能力的要求高。在FAST开启19波束巡天漂移扫描后,数据量激增,每天产生压缩数据50 TB,每年(按200天计算)产生10 PB数据,如何利用好这些数据,是对数据中心存储和超算能力的严峻考验。 另一方面,高效的搜索能力对FAST探测优质毫秒脉冲星具有重要意义。在FAST早期科学数据中心脉冲星分布式搜索计算系统Craber[4]中使用加速度搜索方法[5-7],当参数zmax设置较大时,搜索效率显著降低。目前,Ransom版本的加速度搜索方法[8]虽然在中央处理器上进行了高度优化,但速度仍有欠缺。单机八核处理大小约140 G的巡天漂移扫描数据,zmax参数预设200,耗时约20 h,这仅是10 min巡天且经过处理的数据量。显然,这种数据处理能力极大限制了脉冲双星的有效发现。
此外,双星系统中蕴含大量毫秒脉冲星。如表1和图1中数据,球状星团中包含大量脉冲双星,且多为毫秒脉冲星。截至2020年底,ATNF脉冲星数据库共收录脉冲双星149颗[9],其中,约有130颗在球状星团中发现,表1给出了部分球状星团中样本数据统计结果,图1统计了148颗脉冲星的周期分布(有1颗周期为2.7 s,统计意义不大,未记入),有113颗属于毫秒脉冲星,占双星系统的四分之三,约75.8%,其中,周期为2~4 ms的毫秒脉冲星约占总数的60%。
根据图1的统计结果,双星系统中毫秒脉冲星数量居多。文[10]首次提出毫秒脉冲星是正常脉冲星通过在低质量X射线双星阶段吸积物质而加速到毫秒量级。文[11]也认为当低磁场的中子星吸积物质加速到毫秒级后会演化为双星系统。文[12]模拟的P-P˙图展示了双星脉冲星群自转周期峰值在5 ms左右,并将双星脉冲星群称为毫秒脉冲星群。由此可知,双星系统与毫秒脉冲星存在密切关系。目前,针对双星系统的搜索较为耗时,因此,提高脉冲双星的搜索能力十分必要。
1 脉冲双星系统与加速度搜索
1.1 双星系统及搜索技术
脉冲双星系统是相互绕行的两颗中子星,其中一颗是脉冲星,另一颗称为伴星[13]。通常情况下,当星体自转且磁极波束扫过信号探测设备时,探测设备能接收到一个脉冲信号[14]。传统的周期搜索是对采样信号进行快速傅里叶变换,将时域信号转换到频域,再通过计算频谱功率来寻找周期。在双星系统中,脉冲星受到伴星的引力作用,产生具有加速度的轨道运动,受其影响,脉冲星相对信号探测设备的视向速度发生变化[8]。由于多普勒效应,探测设备接收的星体自旋频率发生变化[15],传统的周期搜索方法不再适用,也难以检测到脉冲星。加速度搜索方法[5-7]可以有效消除这种影响,采用恒定加速度近似轨道运动的加速度,从而消除观测数据中由于双星轨道运动导致的脉冲到达时间的变化[16]。在加速度恒定的假设下,脉冲星的自旋频率在观察者参考系中的漂移速率f˙与加速度a的关系为
(1)
其中,c为光速;f0为脉冲星在自身惯性系中的自旋频率。根据信号处理角度的不同,加速度搜索可以分为时域加速度搜索(Time Domain Acceleration Search, TDAS)和频域加速度搜索(Fourier Domain Acceleration Search, FDAS)[17]。
1.2 时域加速度搜索
时域加速度搜索通过线性展宽或压缩信号的方式对数据进行重新采样,以补偿轨道运动引起的多普勒效应,并在一定范围内不断尝试加速度值,找到最接近真实值的时间序列,再利用周期搜索技术寻找周期信号。重采样时信号的时间间隔为
(2)
其中,v为视向速度;c为光速;τ0为保证正确采样的常数,
(3)
(3)式中,tsamp为采样时间间隔;T为积分时间;a为尝试的加速度值;c为光速。
脉冲星搜索软件包SIGPROC[18]和PEASOUP[19]等应用了信号重采样技术。利用时域加速度搜索方法,文[20]在球状星团中找到了4颗毫秒脉冲星,观测参数见表2。
1.3 频域加速度搜索
频域加速度搜索基于相关性技术[21],可以提高频谱功率。受轨道运动的影响,接收的脉冲星信号频率发生变化,在频谱中表现为某一频率的功率扩散至周围相邻的频率点,导致普通的周期搜索方法失效。文[21]提到,可以将原始信号与邻近信号进行相关操作,从而确定相似程度以恢复信号,这个过程可表示为
(4)
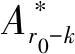
通常认为,在观测时间远小于轨道周期的情况下使用频域加速度搜索方法效果更好,即满足
(5)
其中,Tobs为脉冲星观测时间;Porb为脉冲星轨道运动周期。当观测时间和轨道周期满足(5)式时,加速度可以视为常数,结合多普勒公式有
(6)
其中,c为光速;T为脉冲星观测时间;f为谐波频率;z为假设频率漂移的频率点数量。这样,根据漂移的频率点数z,通过局部信号傅里叶响应的互相关恢复原始信号。
其他周期搜索方法也可以消除双星系统中轨道运动的影响,但应用条件不同。相位调制搜索主要针对观测时间与双星轨道周期大致相同的情况,边带搜索在观测时间远大于轨道周期时效果更好。而加速度搜索的使用条件决定了它的适用目标为周期更小的毫秒脉冲星,在实际中也搜寻到许多优质脉冲星。文[8]首次使用频域加速度搜索方法在球状星团NGC 6544中发现了脉冲星PSR J1807-2459A。文[22]利用频域搜索技术发现了高度偏心的毫秒脉冲星PSR J1946+3417,偏心率达到0.13~0.14,这极为罕见,同时也预示着脉冲星不同寻常的形成过程。
2 频域加速度搜索并行化的必要性及可行性分析
针对频域加速度搜索的并行化提速十分必要。文[16]论述了轨道运动对脉冲到达时间影响很小,在一定条件下不用加速度搜索也可以发现双星。但2020年2月FAST在发现一颗双星的过程中,文[3]将zmax参数设置为300才搜索到脉冲星PSR J1641+3627F。可见,随着搜索要求的不断提高,扩大加速度的搜索范围成为必然,否则数据无法得到有效处理,可能错失优质的脉冲星。
相比时域加速度搜索,频域加速度搜索更快且更适用于并行化。时域加速度搜索将处理过的时间序列全部加载到内存,而频域加速度搜索处理的是局部序列的卷积,更适合小内存的图形处理器进行并行化。对不同加速度值进行处理时,时域加速度搜索需要对每个加速度重采样后的序列进行快速傅里叶变换,而频域加速度搜索只需做一次快速傅里叶变换,再进行相关操作即可。同时,频域加速度搜索可以看作是一个滤波过程,本质是原始信号与滤波器的卷积操作。原始信号长度远大于滤波器长度,计算的时间复杂度约为O(N2),N为信号长度。为提高计算效率,本文使用快速傅里叶变换做循环卷积。首先将原始信号拆分成与滤波器等长度的信号(滤波器中需要补0),再分别与滤波器做卷积并傅里叶逆变换到时域,最后将结果中重叠的部分截去,再合并为输出信号。这一过程也称重叠保留法,可以将算法的时间复杂度降至O(NlgN),如图2。滤波器h中间补充一定长度的0元素,H为其傅里叶变换。将输入信号x分段,每段长为M,每段信号xi向前多取N/2个点,则第1段前面需补充N/2个0,再对每段信号做傅里叶变换得到Xi,Xi与H在复数域中相乘再进行傅里叶逆变换得到A,B和C,将A,B和C中混叠的部分截去得到A′,B′和C′,拼接后得到等价的线性卷积,流程如图3(a)。综上所述,在频域加速度搜索过程中使用循环卷积分段计算所具备的局部内存性是高度可并行的,非常适合并行化计算。

图2 频域加速度搜索中应用的循环卷积Fig.2 Circular convolution in FDAS
3 频域加速度搜索并行化的实现
根据第2节的介绍,程序耗时的矛盾主要在于大量可并行的卷积计算。一方面,我们通过循环卷积来局部缩短时间序列的长度,从而降低内存压力。另一方面,循环卷积中分段后的序列可以利用图形处理器计算单元的局部内存完成运算。本文实现的运算流程见图3(b)。
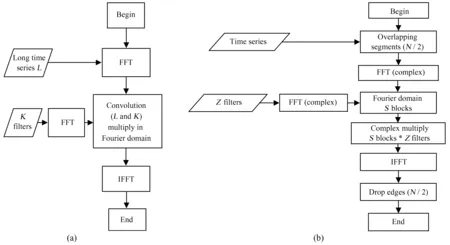
图3 (a)线性卷积运算流程;(b)本文中循环卷积运算流程Fig.3 (a) The flow chart of linear convolution; (b) the process of cyclic convolution in this article
在对循环分段的时间序列进行傅里叶变换时,本文使用CUDA库封装好的cuFFT接口,因为cuFFT接口已针对NVIDIA 图形处理器进行了快速傅里叶变换的高度优化。利用批处理cuFFT例程,在图形处理器上并行调用一次即完成多段序列的傅里叶变换。处理加速度滤波器时,我们在一个图形处理器网格中加载滤波器,其中每个线程加载全部滤波器,然后分段处理经过傅里叶变换后的信号,分别与不同的分段频域信号进行复数域的乘法运算。这一过程在局部进行,且每个线程同步处理相同的运算,再将运算结果写回全局内存进行傅里叶逆变换和重叠段的去除,合并后输出。
4 实验及结果
实验使用AMD Ryzen7 2700X 8核16线程中央处理器,两张GeForce GTX1080显卡,对漂移扫描数据的若干文件(PSR20180811_00A01H, PSR20180826_00A01H, PSR20180828_00A01H和PSR20180902_00A01H, 观测参数见表3)消色散后产生的 .dat文件进行测试,使用不同zmax参数对上述4个文件进行处理,产生相应标记周期信号的ACCEL文本文件,并与CPU版本、GPU版本(https://github.com/jintaoluo/presto_on_gpu)的加速度搜索做了对比,结果见图4。
通过不同方法的比较,结合图4中不同zmax参数对4个超大漂移扫描数据文件的实验处理,结果表明,采用文中方法对加速度搜索程序改进后,本文并行化处理方法耗时相比Ransom版本有极大提升,加速比约10~12倍,较GPU版本也有一定进步,提高约1.5~1.7倍。综合来看,程序的改进有一定成效,达到预期效果。

表3 本次实验使用的观测文件参数Table 3 Observed parameters used in this experiment

图4 不同方法使用不同zmax参数对执行4个文件的消耗时间的对比结果。(a) PSR20180811_00A01H;(b) PSR20180826_00A01H; (c) PSR20180828_00A01H; (d) PSR20180902_00A01H

