基于循环神经网络的水库水位预测方法

纪国良，周 曼，刘 涛，胡腾腾，丁 勇

(中国长江三峡集团有限公司， 湖北 宜昌 443100)

1 研究背景

大型水库重要站点的水位预测是水库防洪中的重要问题，目前主要采用水动力学方法计算。水动力学方法基于严格的圣维南方程组原理[1]，对输入边界条件的准确性有较高要求，当边界条件清晰时，其计算精度很高；否则，容易造成较明显的计算误差。在大型水库的防洪调度中，干流和较大支流的入库流量通常有较为可靠的预报，而水库区间来流则是根据流域降雨情况进行估算，其空间的分布通常难以准确预测，因此区间流量成为最难准确界定的边界条件，使得水动力学方法在计算某些站点的水位精度时难以满足实时应用需求。本文针对这一问题开展研究， 使用基于数据驱动的循环神经网络算法，在区间来流空间分布未知的情况下，提高水库重要站点的水位计算精度。

目前已有许多工作致力于提高水动力学模型的计算精度。长江科学院黄仁勇等[2]在计算三峡水库洪水传播过程时，一方面增加了水库断面测量点数量，降低了断面概化误差；另一方面不断提升入库流量的预报水平并将更多支流加入到模型中。在糙率率定方面，中山大学杨世孝等[3]提出了一种使用最优化方法反求糙率的方式；陈素红等[4]建立了基于多亲遗传算法的河道糙率率定模型；陈一帆等[5]以糙率和水力状态量作为河网非线性动态系统状态变量，采用扩展卡尔曼滤波构建了结合糙率动态校正的河网水情数据同化模型。这些研究已经取得了很大的进展，但在区间来流空间分布难以确定的情况下，其计算精度仍有进一步改进的空间。

本文采用循环神经网络模型[6]，研究干、支流入库流量、坝前水位等因素到重要站点水位的直接映射关系。在应用部分，以三峡水库长寿站水位计算为目标，使用2009—2019年的数据训练、验证和测试模型，应用结果显示在不同的水情分类下，循环神经网络的预测效果优于传统水动力学方法。

2 传统水动力学方法

传统水动力学方法主要是通过求解圣维南方程组[1]来获取断面的水位和流量，一维圣维南方程描述如下。水流连续方程见式(1)，水流运动方程见式(2)。

(1)

(2)

式中：Z表示水位；t为时间；B为河宽；Q为流量；q、v分别为汇入口处的支流流量、流速；A为过水断面面积；g为重力加速度；K为断面的流量模数；0≤x≤l，l表示河长。对于单河道计算，还需要如下初边值条件:

①初始条件。在t=0时，河道每个断面的水位和流量Z|t=0=Z(x)，Q|t=0=Q(x)。

②边值条件。河道的上游入口和下游出口分别给出在任意时刻t的流量过程线Q=Q(t)和水位过程线Z=Z(t)，或者两个边值条件均为流量与水位之间的关系Q=Z(t)；如果是河网计算，还需要给出每个支流的入流过程线Q支=Q支(t)。在水库计算中，一般是应用上游流量过程和下游水位过程作为边值条件。

作为比较，本文亦应用传统水动力学法计算重要站点水位，假设区间流量沿程均匀分布。

3 循环神经网络方法

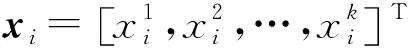
3.1 单层循环神经网络

图1展示了单层循环神经网络结构，其中W和U是网络参数，h是相应节点的隐藏状态，x是输入向量，下标t表示时刻。它的计算顺序遵从时间的先后顺序，从左至右逐步合成特征向量的信息，完成特征的提取过程。其中每个矩形代表一个计算节点，常用的计算节点有传统节点、LSTM(Long Short-Term Memory)[7]节点和GRU(Gated Recurrent Unit)[8]节点，具体计算方式如下。

图1 单层循环神经网络结构Fig.1 Structure of recurrent neural network of a single layer

传统计算节点公式为

ht=σ(Wxt+Uht-1+b) 。

(3)

式中:b是偏置项参数;σ(x)=1/(1+e-x)是sigmoid函数[9]。

LSTM计算节点公式为：

(4)

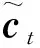
GRU计算节点公式为

(5)

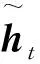
与传统计算节点相比，LSTM和GRU节点可以有效避免梯度爆炸或者梯度消失现象[7-8]，能够处理更长序列的数据；LSTM与GRU相比，前者的计算量比较大，对数据量的要求较高，但是二者在许多任务上的效果近似。考虑到本文研究问题的数据规模，选择GRU节点进行实验。

在预测任务中，将网络中最后一个计算节点的隐藏向量hn看作模型的预测值，假设共有N个样本，hn,i表示第i个样本的预测值，yi表示第i个样本的实测值，则定义目标函数为

(6)

式中：λ是系数，第一项是最小二乘项，使得预测值尽可能接近实测值；第二项是正则项，能有效防止模型过拟合。

3.2 深层循环神经网络

对于复杂型数据，单层循环神经网络有时候难以学习数据之间的映射关系，需要加深网络层次。图2是深层循环神经网络结构图，深层循环神经网络是多个单层循环神经网络的叠加，下一层的输出是上一层的输入，先计算第一层，计算完毕后，第一层所有节点的隐藏状态作为第二层的输入，然后再计算第二层，依此类推，直到最后一层计算完毕。最后一层最后一个节点的输出是整个网络的输出，记为hm,n，表示第m层的第n个节点的输出。与式(6)相同，目标函数定义为

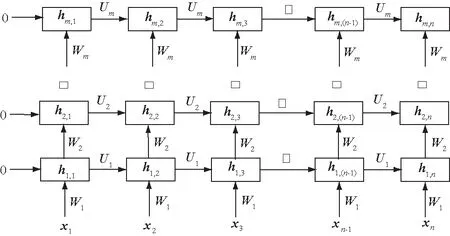
图2 深层循环神经网络结构Fig.2 Structure of recurrent neural network of multilayer

(7)

4 模型的搭建和求解方法

本文在构建模型和求解方面使用基于图结构的建模语言TensorFlow[10]实现。TensorFlow是基于python[11]开发的软件包，是一个采用数据流图架构设计、用于数值计算的开源软件库，能够自动地根据变量之间的依赖关系运用链式法则求导梯度，方便模型建立和求解。

5 三峡水库长寿站水位计算

三峡水库蓄水运用以来，根据以往的研究成果和实际运行管理经验，长寿区域是回水敏感区域，该区域长寿站是库尾重要的水位控制性站点，是研究的重点，因此本文选择长寿站作为研究对象。

5.1 样本构造

三峡水库地域广，涉及到的支流众多，结合圣维南方程组的计算原理和实际经验，选取影响长寿站水位的主要因素为三峡入库流量、寸滩流量、武隆流量、出库流量和坝前水位。其中寸滩处于长寿的上游，是上游来水的代表站；“三峡入库流量”指的是三峡水库库总的来流量，包含区间流量，这里不考虑区间来流的空间分布；武隆站是长寿下游乌江的控制站点，其来水对长寿站水位具有较显著的顶托作用；出库流量和坝前水位反映的是水库出口的控制条件。

在主要因素选取之后，需要考虑影响当前长寿站水位的时段数。考虑到洪水调度实际情况，水文预报是间隔6 h一个值，因此相邻时段的间隔取6 h；由于寸滩流量对长寿站水位的影响最大，且水流从寸滩到达长寿站平均时间约6 h，因此长寿站水位预报计算的输入取2个时段数据为宜，即当前和6 h前两个时刻。表1和表2给出了一个样本的示例，表1是模型的输入，表2是模型的输出，即若要预测2018年1月1日 10时长寿站的水位，则需要给出2018年1月1 日4时和2018年1月1日10时三峡入库流量、寸滩流量、武隆流量、三峡出库流量和凤凰山水位(坝前水位)。在实际使用时，均使用水文预报数据，因此本方法的预见期同水文预报预见期。

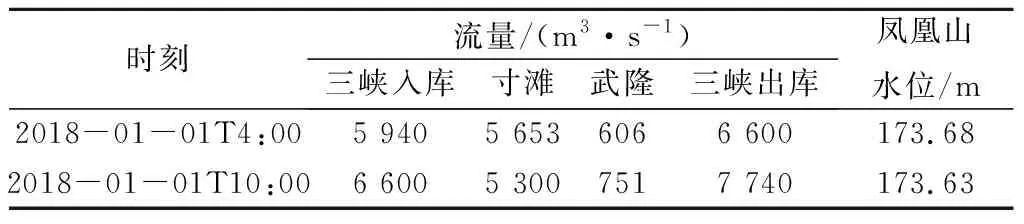
表1 样本输入示例Table 1 Feature vectors of a sample

表2 样本输出示例Table 2 Outputs of a sample

根据第3节描述的数学形式，预测2018年1月1 日10时长寿站水位时模型的输入为

同时，模型输出为173.75 m。考虑到流量和水位的单位不同，以及神经网络的输入值不宜过大(否则其非线性项梯度接近0，模型无法优化)，需要将向量进行归一化处理，同时消除单位和数值大小的影响，流量和水位的归一化处理如下：

归一化值=(当前值-最小值)/(最大值-最小值)。

在收集的数据中，流量最大值为71 200 m3/s，最小值为995 m3/s；最高水位为177.09 m，最低水位为145 m，因此归一化后得到模型的输入向量为

对应的模型输出为0.898 4。经过上述处理，水位、流量的数值均无量纲，且压缩在区间[0,1]内，在预测应用时按照逆过程还原即可获得水位值。

5.2 数据收集和水情分类

为了使数据样本涵盖不同种类的水雨情，本文收集2009年1月1日0时至2019年11月18 日23时的历史运行数据，共95 376条小时数据，其中2009—2018年的数据用于训练和验证模型，2019年的数据用于测试模型。由于不同时期的坝前水位和入库流量差别较大，因此需要根据不同的坝前水位和入库流量进行分类，针对每个类别单独训练模型。三峡水库2009—2019年入库流量的取值范围是[3 320, 71 200] m3/s，坝前水位的范围是[145, 175]m，综合考虑不同水情和模型对数据量的要求，共分为7类，其中样本根据5.1节的描述生成，训练集和验证集是对样本(由2009—2018年数据生成)按照90%和10%随机划分生成；测试集是2019年数据生成的样本。生成样本的数据分类情况如表3所示。

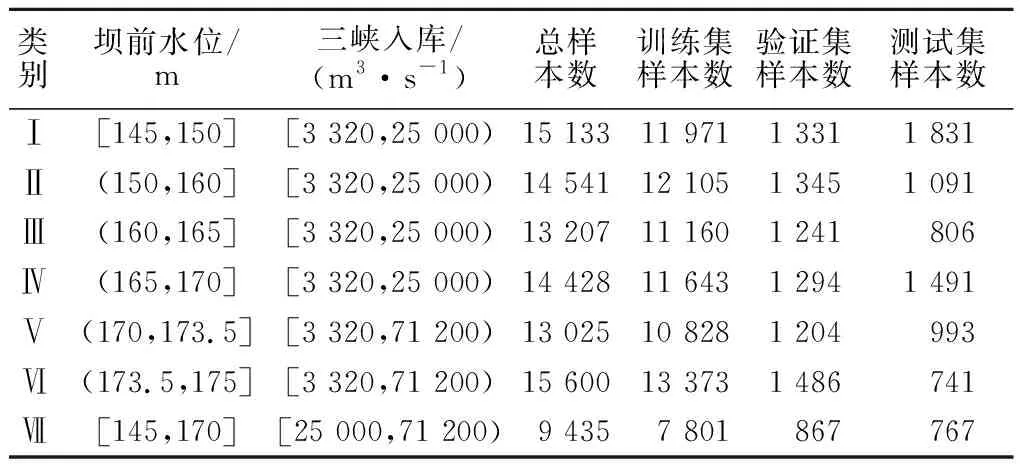
表3 数据分类情况Table 3 Data of different classes

5.3 模型超参数设置

在5.2节中，根据不同的水情将数据分成了7个类别，需要对每个类别设置网络的层数、每层隐藏节点个数、优化算法学习率α、正则项系数λ、批量训练样本数等超参数。超参数的选择首先根据经验确定范围，然后在验证集上测试其效果，选择验证集上效果最好的超参数。表4给出了最佳的超参数设置。

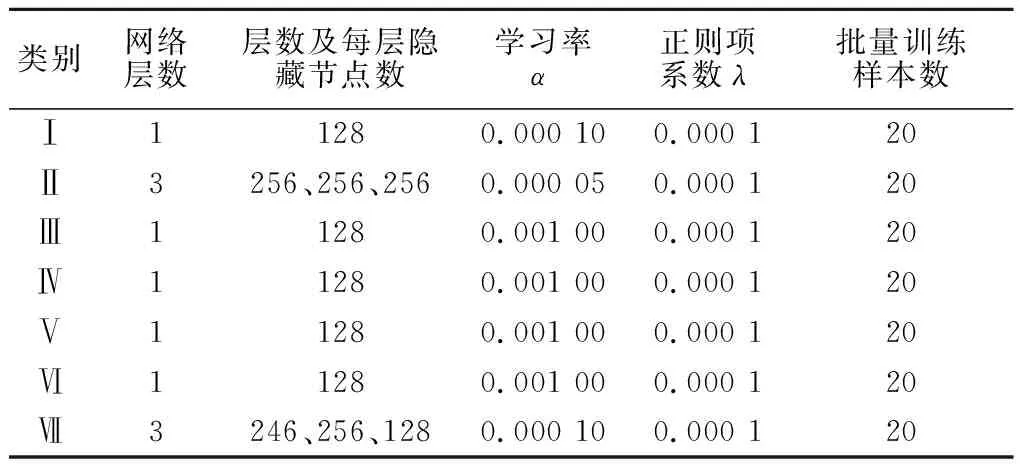
表4 超参数设置Table 4 Setting of hyper-parameter

5.4 试验结果和误差分析

5.4.1 试验结果的整体比较

图3(a)是2009—2019年所有样本(包含所有类别的训练集、验证集和测试集 )的计算水位和实测水位对比图，具体时间是从2009年1月1日 6时至2019年11月18日 17时。图3(b)是对应的误差分布，表5是7个类别的训练集、验证集和测试集的误差上下限。

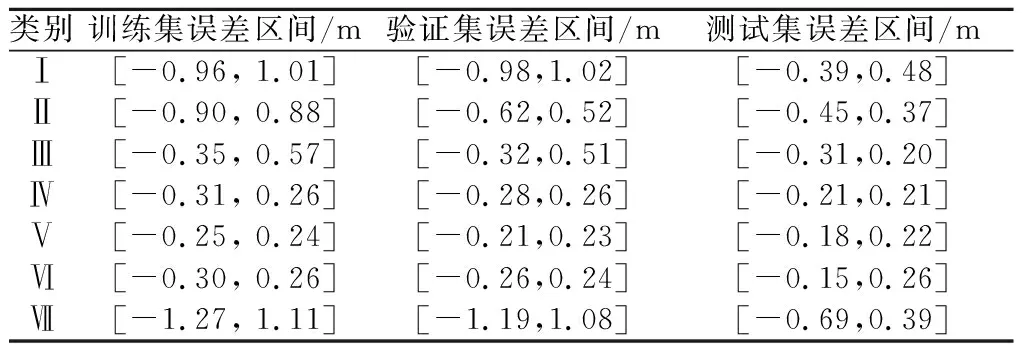
表5 不同类别的训练集、验证集和测试集误差范围Table 5 Error ranges of training, validation,and test data sets

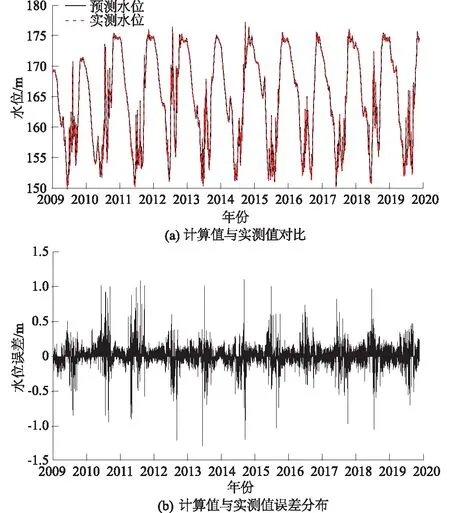
图3 2009—2019年长寿站水位计算值与实测值对比和计算值与实测值误差分布Fig.3 Comparison between calculated and measured water levels of Changshou station from 2009 to 2019

由图3可知，预测水位曲线与实测水位曲线距离很近，说明模型对数据的拟合和预测效果较好。

在水位较高时，预测线和实测线几乎重合，计算精度较高，满足实际应用的需求。从表5中可以看出，较大误差主要发生在Ⅰ、Ⅱ和Ⅶ类中，且Ⅰ和Ⅶ类均出现了超过1 m以上的误差。Ⅰ、Ⅱ类误差较大的原因是坝前水位较低，河槽较窄，流量略微增大后水位就会有显著变化，因而计算难度较大；Ⅶ类是三峡入库流量在25 000 m3/s以上，坝前水位在170 m以下的条件，此时入库流量较大，水位变化幅度大，预测难度相应增大，因此最大误差有-1.27 m。以上2种情况都发生在长寿站水位较低时，因此不影响实际中的应用。

5.4.2 与传统水动力学法比较

2010年、2012年、2014年、2017年是长江流域典型洪水年，其中2010年、2012年、2014年洪水发生在汛期，2017年发生在蓄水期。

图4分别是2010年、2012年、2014年、2017年长寿站实测水位、水动力学法计算水位和循环神经网络计算水位的对比。从图4可以看出，较大误差多发生在水位低的情况下；在高水位时2种计算方法的误差都显著缩小；比较2种计算方法的误差，循环神经网络的误差在绝大多数情况下小于水动力学方法，说明了本文方法的有效性。

图4 不同年份水动力学法与循环神经网络法对比Fig.4 Comparison of the prediction result between hydrodynamic method and recurrent neural network under different water regimens in different years

5.4.3 循环神经网络方法有效性的原因分析

循环神经网络的输入实际上采用的是水动力学方法的边界条件，它的有效性可以归纳为以下两点：

(1)循环神经网络能有效避开区间流量空间分布未知的问题。在水动力学方法中，圣维南方程组经过离散和线性化以后，求解的过程是依靠坝前水位逐步向上游计算各断面的水位，上游断面的水位对下游断面水位具有很强的依赖关系，当区间来水空间分布未知时，水库中间的部分断面水位计算就会产生误差，由于递推关系，这些误差会向上游传播，最终导致长寿站水位计算误差较大。循环神经网络方法只使用了区间来流的总流量(包含在入库流量中)，忽略了其空间分布，反而模拟效果更好，主要原因是在大多数情况下，由于距离较远，区间来流对长寿站水位的顶托作用较小，尽管区间来流会影响库区中间的水位，但是模型的输入只依赖坝前水位，并不依赖中间水位，所以能有效避开区间来流的空间分布问题。诚然，当区间流量空间分布未知时，上述2种方法都只适用于区间来流占比较小的情况，占比较大时都会产生较大的计算误差。

(2)循环神经网络没有使用地形资料和糙率参数，避免了数据测量误差和率定误差，因此能提高预测精度。

6 结 论

(1)在大型水库重要站点水位计算中，循环神经网络方法是直接挖掘输入数据到输出数据的关系，降低了边界条件准确性的要求，只需要使用库周入库流量，有效避开了区间来流空间分布未知的问题；同时也不需要使用地形资料和糙率参数等，没有测量和率定误差，因此它的预测精度较高，并且精度会随着运行数据的积累而不断提高。

(2)循环神经网络可应用于其他问题的研究。由于水文领域的数据均具有时间属性，非常适合此种网络结构，因此它可在流量、水文、泥沙等方面进行推广。

(3)考虑到三峡库区一直处于淤积过程中，局部集中淤积会对库水位产生较大影响，神经网络模型训练使用的数据包含了淤积前和淤积后，数据前后的一致性略有差别，本文下一步工作是研究泥沙淤积对水位计算的影响。