深度优先搜索算法的应用研究
◆王远敏
深度优先搜索算法的应用研究
◆王远敏
(兴义民族师范学院信息技术学院 贵州 562400)
在算法的应用中,深度优先搜索算法在图结构的数据类型中有着广泛的应用,本文设置了两个应用场景,一个是信件能否送达问题,一个是不重复打卡夜跑路线的规划问题,这两个问题都与现实生活息息相关。本文通过对这两个问题的详细分析和解决来说明深度优先搜索算法的各种不同使用场合和方法,同时也分析了在解决问题过程中存在的不足。
深度优先;搜索算法
1 引言
深度优先搜索是遍历图的其中一种顺序,在图结构的数据类型中有着广泛的应用,从最基本的结点遍历问题,到判断图的连通性问题,再到最短路径及旅游路线规划问题,都可以使用深度优先搜索算法进行求解。因此深度优先搜索算法在各种问题的算法设计中有着广泛的使用,发挥着极其重要的作用。以下从两种常用情景讨论深度优先搜索算法的设计使用过程,并进行应用的比较分析[1]。
2 使用情景
该文选择了两种与实际工作和生活联系起来的问题:一是信件能否送达问题,二是不重复打卡的夜跑路线规划问题。通过问题的分析及实现来研究深度优先搜索的使用方法和过程。
2.1 信件能否送达问题
假设现有由x个信息收集员组成的信件相互交换信息网,在这x个信息收集员中可直接传递信件的路线有y条,路线没有方向之分,需要判断每当一个信息收集员退出信息网后,信件还能否送达到其他信息收集员处。
首先对该问题进行数据结构的设计,将x个收集员看成是结点,y条可直接传递信件的路线看成是边,则可得到对应的数据结构为一个无向图。每当一个信息收集员退出信息网,则在该图中减少一个对应的结点及与其相连的路线(即对应的边),然后通过判断剩余信息收集员及路线是否连通来确定信件能否送达,在此采用深度优先搜索遍历进行连通性判断。
解决该问题的第一步采用邻接矩阵对映射后的数据信息进行存储,这也为后续采用深度优先遍历做好准备。设置存储类型如下:
typedef struct IGnode *DToG;
struct IGnode{ int x,y; int G[100][100];};
接下来设置深度优先搜索算法为单独函数,方便后续进行调用。算法如下:
void IGS(PToG mailweb,int V,void(* search)(int))
{ int w;
search(v);
searched[v]=1;
for(w=0;w
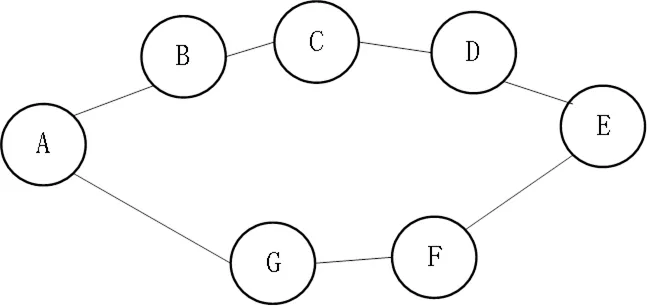
if(!searched[w]&&(mailweb->G[v][w] IGS(mailweb,w,search); } 最后在每一次信息收集员有变化时对信件送达网络进行搜索、连通性判断,并给出提示,当信息收集员减少到无法连通时信件将无法进行相互送达,输出结论,问题得以解决。设置数据案例,假设初始信息收集员有10人,即x=10;相互之间可以直接传递信件的路线有9条,即y=9。10个信息收集员用编号0到9代表,相互之间传递信件的路线使用数据对来表示,即{(0,1),(0,2),(1,3),(0,4),(2,5),(3,6),(2,7),(4,8),(3,9)}。设计一个函数LCS通过调用深度优先搜索算法来判断当前信件送达网络的连通分量数,在主函数中进行判断,若当前连通分量数大于1则得出结论信件不能实现整个信息网的送达[2]。LCS算法的主要实现如下: int LCS() { int v;int count=0; for(v=0;v { if(vis[v]==false&&lost[v]==false) { count++; IGS(v); } } return count; } 在该算法中通过调用深度优先算法来判断现有信件送达网络的连通性问题,若一个连通分量结束则循环调用探索另一个连通分量,以此统计出信件送达网络存在的连通分量。若连通分量的计数器的值为1,则说明整个网络的信件送达没有问题;当信息收集员减少到使得整个信件送达网络的连通分量数大于1时,则说明整个网络的信件无法相互送达。接下来是主函数的设计,在主函数中输入信件送达网络的原始数据,通过调用LCS来统计原始网络的连通分量数量,若一开始就不具备信件送达条件的话,则输出否定信息之后终止执行,不再判断当信息收集员变少的情况;否则在每个信息收集员减少一个就循环调用LCS函数进行连通分量的计数和判断,若信息收集员减少后连通分量数还是等于1,则得出结论信息网正常,若减少一个信息收集员后连通分量数大于1,则得出结论信息网不能再继续相互送达。主要语句及运行结果如下所示: 从第一个问题可以得出,深度优先搜索对于图结构的连通性相关问题可以提供一种解题的思路,而很多与路线相关的问题都可以转换为图结构进行存储。该题目中需要判断的是在信息收集员不断变化的情况下判断信件是否能送达,经过转换之后设计的解决方法是每个信息收集员减少后就采用深度优先搜索判断剩余的信息收集员组成的图结构是否是连通的,将信件能否送达先转换成站点的连通性判断,再使用深度优先搜索算法进行连通性判断,从而解决问题。 当然在该问题中,可以对信件送达网络的送达进行扩展,当信息收集员减少导致整个网络不连通时,可以通过增加设置站点管理员,也就是每个连通分量设置一个负责人,负责人之间可以相互进行信件的送达,这样就可以避免连通的限制。 很多人在忙碌的工作和学习中都有夜跑的习惯,以此作为保持身体健康的重要锻炼手段。夜跑中我们希望不走重复的景点以提高自身夜跑的积极性,因此在夜跑路线中想规划一条从起点出发经过不重复景点最后再回到起点的路线。假设夜跑场地如图1所示,A为起点,B、C、D、E、F、G为可以经过的景点,景点间有直达路线的话则在两景点间画一条线表示。 图2 夜跑场地示意图 首先对该问题进行分析并设计其对应数据结构。将每个景点看成顶点,可直达的两景点间的路线看成边,则对应于一个图结构数据类型。但与前一种情景不同的是在这个问题中每个景点只能经过一次,如果对应成图结构需要进行拆点,例如景点B对应的结点x要拆成x和x’两个结点,再将x和x’之间连接一条边,由于每个中间景点不能重复经过,所以可以设置边的容量是1,单位流量费用则为0。当景点B到景点C有直达道路时,设置结点x’到结点y存在一条边(其中y为结点C拆成结点之一),该条边的容量同样是1,单位流量费用设置成-1,便于统计经过尽可能多的景点数。这样该问题就转化成了最小费用最大流问题[3]。 解决该问题的思路是先设置数据的存储结构,根据预设的数据,景点总数n等于7,景点之间直达路线的条数m等于7,采用二维数组存储顶点及其路线信息,采用结构体数组存储路线信息,其中包括路线连接的两个景点信息、路线边的容量和单位流量费用。这样的话便于统计最多可以经过的不重复景点的个数。数据类型设置如下: 将夜跑路线所构成的图结构基本信息输入进行初始化以后,从夜跑起始点A出发,沿着路线容量为1的景点进行深度优先搜索,最终返回到夜跑起点,在进行设置的时候只有夜跑起点的路线容量为2,这样就可以实现不经过重复的景点进行夜跑路线的设置。其次需要解决的是如何经过最多景点的问题,在进行深度优先搜索的同时带入单位流量费用的判断,也就是借助最大流算法来进行规划。在此过程中,深度优先搜索是主要的路线规划算法。 void DFS_Flow(PToG run,int V,void(* search)(int)) { int w; search(v); searched[v]=1; for(w=0;w if(!searched[w]&&(run->G[v][w] DFS_Flow(run,w,search); } 最后得出根据初始设置的地图得到的夜跑路线规划为以下输出结果(图3): 从该案例可以看出,深度优先搜索在夜跑路线规划问题中的应用是一种扩展式的应用,除了搜索连通分量以外还结合了最大流算法来进行使用。 对这两个不同的使用情景进行比较分析,第一个场景使用了深度优先搜索算法来进行图的连通分量的统计,使用方法更加的直接,通过循环调用该算法来进行,在深度优先算法中没有其他的扩展。在第二个场景中,问题相对复杂,除了进行图的连通性判断以外,还要计算经过的景点的数目,且不允许经过重复的景点,因此在使用深度优先搜索算法时增加了最大流算法,可以说是一种融会贯通的算法设计思路。 在以上两个案例中,题目的初始数据都是图形结构的,且在题目的要求中都涉及图的路线的问题,以此可以从遍历来考虑,而深度优先搜索遍历则是一种可以结合队列和堆栈来进行的遍历方法,因此可以用来解决很多的问题,在实际应用中也有很多其他扩展的用法。当然在以上案例中的初始数据设置都较为简单,并且在解题的过程中忽略了很多其他的影响因素,因此还有很多需要改进的地方,将在以后的研究中进行改进和扩充。 [1]陈越.数据结构(第2版)[M].北京:高等教育出版社,2016. [2]陈越.数据结构学习与实验指导(第2版)[M].北京:高等教育出版社,2019. [3]陈小玉.趣学算法[M].北京:人民邮电出版社,2017.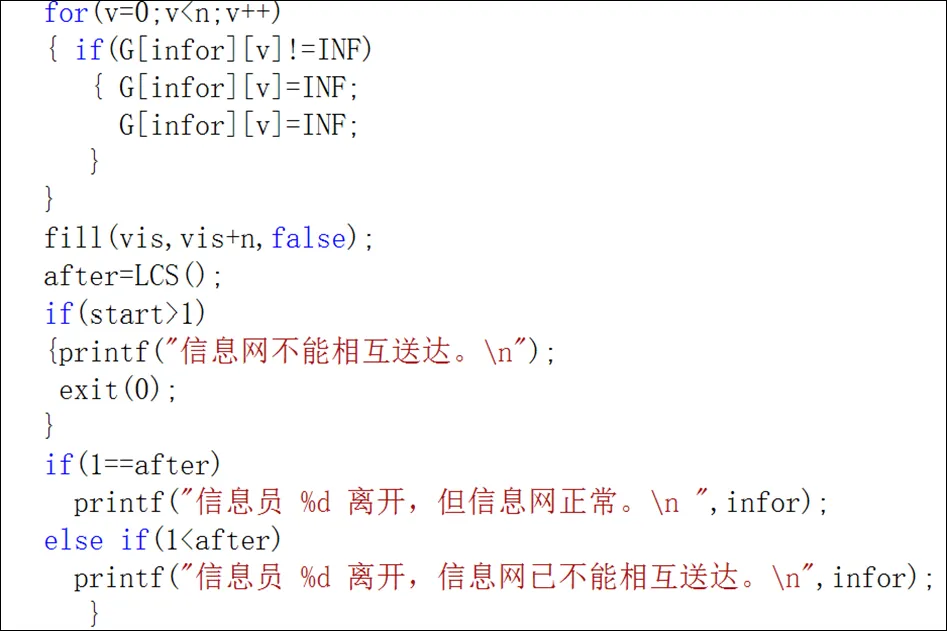
2.2 不重复打卡的夜跑路线规划问题


3 比较分析
4 小结

