基于近似信息熵和随机森林的网络安全态势要素提取研究

◆杨乐 王新辉 樊龙飞

基于近似信息熵和随机森林的网络安全态势要素提取研究

◆杨乐 王新辉 樊龙飞

（公安部第一研究所 北京 100048）

针对态势要素提取问题，提出了一种基于近似信息熵改进随机林的网络安全态势要素提取方法。首先，属性的重要性由近似信息熵约简取得。再使用随机森林分类器对处理后的数据进行分类。最后，为了验证算法的有效性，通过入侵检测数据集测试改进随机森林算法性能。实验结果表明，该算法对比传统随机森林有效地提升了准确率，提高了网络安全态势要素提取水准。

近似信息熵；随机森林；态势感知要素

1 背景

网络安全领域相关研究在近年来发展迅猛。随着互联网环境不断变化，网络拓扑结构日趋复杂，相关网络攻击也随之增加。为从整体上把握系统的网络安全状况以应对日益复杂和相对隐蔽的网络攻击，研究网络安全态势感知成为一个新的发展趋势。网络安全态势感知是对整个系统网络安全状态感知过程，包括态势要素的提取、评估和预测。网络安全态势感知前提是态势要素提取，要素提取过程是态势感知的重要组成部分。

目前，国内外对于态势要素提取主要有两个研究方向[1]：一种基于先验知识的方法、另一种基于数据挖掘、机器学习等技术分析各行为之间的关系。BASS[2]在1999年提出了网络安全态势感知的概念，其通过入侵检测系统检测结果，分析攻击信息以评估网络安全。Poolsappasit[3]提出了使用贝叶斯网络对网络态势评估，该方法在不同级别量化网络态势要素，给予决策者更多的信息对网络态势进行评估。国内主要从入侵检测的角度研究态势因素提取，不仅可以去除态势要素中的冗余特征，还可以有效地检测攻击行为。孙磊[4]提出了采用LOF算法在少数类样本点中提取出空间距离较大的离群样本点，防止由于少数类别的样本点中存在离群点，使得各类别数据达到相对平衡状态。周莉[5]提出了利用决策树算法建立联级网络安全态势感知模型，利用时间窗口切分网络和主机流量以提升决策树分类处理准确度。

上述方法需要大量的先验知识提取态势感知因素的过程，具有较强的主观性。该类方法对特定字段有一些效果，但是随着样本库增大，使用基于先验知识分析方法会损失一定的效果。因此，本文提出了一种基于近似信息熵改进随机森林提取态势要素的方法，将近似信息熵引入网络安全态势要素提取，使用近似信息熵计算属性权重，选择重要性较高的属性以删除冗余属性，有效地提高了随机森林分类精度。

2 基于近似信息熵改进随机森林的态势要素提取

态势要素提取的主要任务是在复杂的异构网络中准确地发现异常行为，其实质是筛选态势要素特征集的过程。通过去除冗余属性和属性降维，选择相关性较高的属性。在复杂的异构网络中，网络流量信息具有数据量大、属性类型多样的特点。因此，对于大规模的交通信息，降维、冗余和提取关键属性集已成为入侵检测的重要过程。有PCA[6]（主成分分析），SVD（奇异值分解）和近似信息熵用于属性约简。PCA和SVD方法可能会丢失一些关键信息，而近似信息熵方法具有学习能力，不需要数据集以外的先验知识，且不会改变原始数据中的关键决策信息。图1为近似信息熵的约简过程。

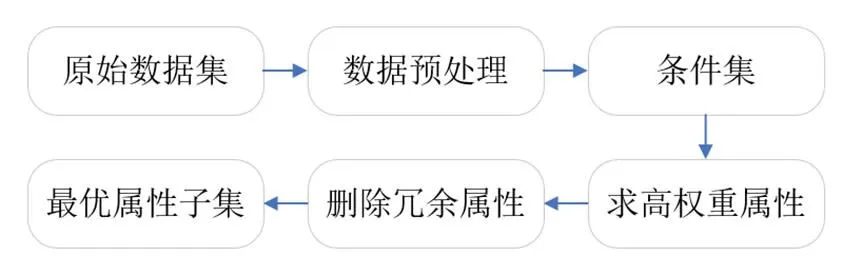
图1 基于近似信息熵约简的态势要素提取

态势要素决策表DT为元组，DT=（U，C，D，V，F），其中U是原始数据集；C和D分别为特征属性和决策属性集；V是所有属性；函数f：U×（C∪D）→V，其中∀a∈C∪D、x∈U，f（x，a）∈Va。

对于决策表DT=（U，C，D，V，f），另U/IND（D）={Y1，Y2，…Ym}，任意∀B∈C，另U/IND（B）={X1，X2…Xn}，定义决策表近似信息熵属性D的近似值B为：

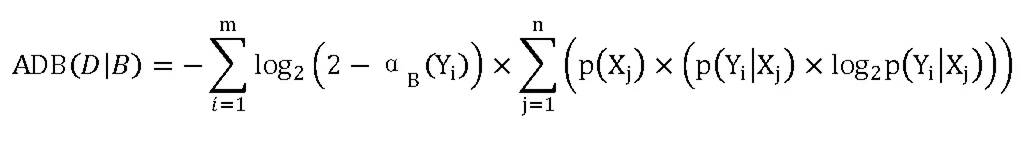
2.2 随机森林

随机森林是基于决策树的Baging集成学习算法[7]。决策树是一种应用十分广泛的分类算法。在决策树停止生长前，树中的每个叶子节点都按照分裂准则进行持续分类。在构造决策树的过程中，最重要的一步是根据分割准则确定最优分割特征。常见的决策树算法有ID3、C4.5和CART决策树算法。

随机森林相当于多个决策树的组合。随机森林采用bootstrap方法从原始数据集中提取相同大小的样本，形成M个子数据集，然后构造相应的M决策树形成决策林，但各决策树之间没有相关性。当每个节点拆分时，决策树从所有K个特征中随机抽取一个特征子集（通常为log2K），随后从子集中选出最优拆分的特征集来构建树。当输入一个新样本时，对森林中的决策树进行逐个判断，最终的分类结果由M个决策树的输出决定。与普通决策树相比，随机森林不易陷入过度拟合，并且具有良好的抗噪性、快速的训练速度和处理高维数据的能力。

2.3 基于近似信息熵随机森林的态势要素提取

要素之间的重要性和分类作用不同，在使用传统随机森林时没有属性降维和数据降噪会对分类结果产生影响。通过属性约简，可以对高维数据进行降维，从而减少分类训练的数据量，同时保留数据中的关键信息并消除数据中的噪声。因此，本文提出了一种随机森林使用近似信息熵进行属性约简的态势要素提取方法，结合近似信息熵和随机森林以提高准确性。

3 实验过程与分析

3.1 实验数据

实验数据集采用的是UNSW_NB15数据集，数据集使用IXIA PerfectStorm工具生成9大攻击类型，生成两个已标记数据集用于学习研究的UNSW_NB15_training-set.csv和UNSW_NB15_testing-set.csv，train和test数据集分别有182600和82330条数据，该数据是使用Argus、Bro-IDS及其他生成算法生成的，具有42维特征。

该实验使用了Weka，一种广泛应用于数据挖掘的开源机器学习工具。本文用CART决策树构造了一个随机森林。UNSW_NB15数据集中有大量连续数据，需要对数据进行离散化。计算离散化数据上每个属性的信息增益，删除冗余属性时，阈值设置为0.5，数据分别导入传统随机森林分类模型和改进的随机森林分类模型，并对改进后的阈值进行调试，选择最佳阈值。阈值对分类效果的影响如表1所示。

表1 阈值对分类的影响

阈值00.250.50.751准确率0.7170.7640.8910.8300.733错误率0.2830.2360.1090.2700.267

从表1中可知，最佳阈值设置为0.5。经过约简算法的计算删去了数据集中dur、sttl、dttl、源IP、源端口、目的IP、目的端口等冗余属性。

表2显示了使用传统随机森林分类模型和基于近似信息熵约简的随机森林分类模型对UNSW_NB15数据集进行分类的比较结果。

表2 约简前后随机森林分类准确率对比

类型约简前准确率（%）约简后准确率（%）Normal0.8930.933Analysis0.7920.887Backdoor0.8070.880DoS0.7190.899Exploits0.8800.875Fuzzers0.8110.894Generic0.9180.952Reconnaissance0.8600.944Shellcode0.8360.932Worms0.8910.897

从实验中可以看出，UNSW_NB15数据集中基于近似信息熵约简改进的随机森林算法在分类的准确性方面优于传统的随机森林算法。

表3展示了在属性约简改进随机森林后与朴素贝叶斯、KNN、SVM分类器检测NSL-KDD数据集的情况。分类结果对比如表3所示。

表3 阈值对分类的影响

分类器朴素贝叶斯KNN随机森林改进随机森林准确率0.7340.8460.8910.935错误率0.2660.1540.1090.065

从表3可以看出，与传统算法相比，随机森林分类器的分类精度最高；近似信息熵属性约简改进的随机森林分类器的精度相比传统随机森林也有所提高。

综上所述，基于实验结果我们可以得出，本文提出的基于近似信息熵属性约简改进的随机森林算法能够有效提高准确率，实现网络安全态势要素的高效提取。

4 结论

将近似信息熵与随机森林相结合，提出了一种基于近似信息熵属性约简改进随机森林提取态势要素的算法。首先利用近似信息熵属性约简对态势要素集进行降维，删除冗余态势要素，随后利用随机森林对降维后的态势要素集进行分类训练，提取权重高的要素，为网络安全态势评估、预测提供了关键数据集。

实验结果表明，相对于传统的随机森林算法，改进后的算法有效地提高了准确率，提升了网络安全态势要素提取准度与精度。

[1]常镒恒，马照瑞，李霞，等.网络安全态势感知综述[J].网络空间安全，2019，10（12）：88-93.

[2] Bass T，Gruber D. A glimpse into the future of id[J]. login：： the magazine of USENIX & SAGE，1999，24：40-45.

[3]Poolsappasit，Nayot，Dewri，Rinku，Ray，Indrajit. Dynamic Security Risk Management Using Bayesian Attack Graphs[J]. IEEE Transactions on Dependable and Secure Computing，2012（1）.

[4]孙磊. 基于随机森林的工控网络安全态势要素提取方法研究[D].长春工业大学，2021.

[5]周莉，李静毅.基于决策树算法的联级网络安全态势感知模型[J].计算机仿真，2021，38（05）：264-268.

[6]Ho TK. The random subspace method for constructing decision forests [J]. IEEE transactions on pattern analysis and machine intelligence，1998，20（8）：832-44.

[7]Moustafa N Slay J. UNSW-NB15：a comprehensive data set for network intrusion detection systems（UNSW-NB15 network data set）[C].2015 military communications and information systems conference（MilCIS）. IEEE，2015：1-6.