基于攻防博弈的网络防御决策方法研究综述

刘小虎，张恒巍，马军强，张玉臣，谭晶磊

基于攻防博弈的网络防御决策方法研究综述

刘小虎，张恒巍，马军强，张玉臣，谭晶磊

（信息工程大学，河南 郑州 450001）

博弈论研究冲突对抗条件下最优决策问题，是网络空间安全的基础理论之一，能够为解决网络防御决策问题提供理论依据。提炼网络攻防所具备的目标对立、策略依存、关系非合作、信息不完备、动态演化和利益驱动6个方面博弈特征。在理性局中人假设和资源有限性假设的基础上，采用攻防局中人、攻防策略集、攻防动作集、攻防信息集和攻防收益形式化定义了五元组网络攻防博弈模型，分析了博弈均衡的存在条件，总结出基于攻防博弈模型的网络防御决策过程。梳理分析了基于完全信息静态博弈、完全信息动态博弈、不完全信息静态博弈、不完全信息动态博弈、演化博弈、微分博弈、时间博弈和随机博弈共8种不同类型博弈模型的网络防御决策方法的适用场景，综述其研究思路，给出基于不同类型博弈模型的网络防御决策方法的优缺点。总结基于攻防博弈的网络防御决策方法的发展过程，说明防御决策方法具备的优势特点；指出研究过程中面临着博弈建模考虑因素与模型复杂度的关系，博弈推理对信息和数据的依赖性，博弈模型的泛化性和迁移性3个问题；并从规范策略的描述机制、优化收益的计算方法以及与其他网络安全技术相互融合3个方面展望了下一步研究方向，说明需要重点解决的问题。

网络防御；决策方法；攻防博弈；博弈特征

0 引言

网络攻防过程中，攻击方和防御方可能有多种策略可供选择。针对特定的攻击策略，不同的防御策略会产生不同的安全收益[1]。受资源、能力和偏好等方面限制，防御方面临着优化配置防御资源、选取最优防御策略、实现收益最大化的决策问题[2]。

传统的网络防御决策方法较多依靠经验的主观判断，难以为网络安全管理人员选取防御策略提供有效、可信的建议。网络防御决策应从决策分析角度，依据科学的决策理论和方法分析推理可选策略，筛选得出最优防御策略，实现自身收益最大化。博弈论是运用数学方法分析冲突对抗条件下个体互动行为及其可能产生后果的理论，在经济学[3-4]和管理科学[5-6]中得到了广泛的应用。博弈论能够解决策略相互依存环境中如何决策以获得最大收益的问题，为描述网络攻防矛盾冲突提供了一种数学框架[7]，被认为是网络空间安全学科的基础理论之一[8]，在解决网络安全问题中应用越来越广泛。文献[9-13]对基于博弈论的网络安全相关研究进行了综述。

近年来，基于攻防博弈的网络防御决策方法成为研究热点[14-18]，亟须加以综述。本文提炼网络攻防博弈特征，形式化定义网络攻防博弈模型，对比基于不同类型攻防博弈模型的网络防御决策方法的适用场景和优缺点，总结方法的发展过程、优势特点和面临问题，给出下一步重点研究方向。

1 网络攻防博弈特征分析与模型定义

1.1 网络攻防博弈特征分析

网络攻防博弈特征主要表现为目标对立、策略依存、关系非合作、信息不完备、动态演化和利益驱动6个方面。

（1）网络攻防双方的目标相互对立

网络攻防过程中，攻防双方都有明确的目标。攻击方通过选取不同的攻击策略向防御方发起攻击，意图破坏目标网络系统的机密性、完整性和可用性等安全属性，使自身收益达到最大[19-20]；防御方通过选取不同的防御策略实施防御行动，目的在于保护己方网络系统的机密性、完整性和可用性等安全属性不被破坏，使自身遭受攻击后的损失降到最低。因此，网络攻防双方目标完全对立、利益针锋相对、矛盾不可调和，具有鲜明的对抗特征。

（2）网络攻防双方的策略相互依存

网络攻防对抗中，攻防双方行动彼此制约、相互影响，对抗结果由双方策略共同决定。防御效果不仅取决于防御策略本身，还受制于攻击策略；攻击效果不仅取决于攻击策略本身，还受防御策略影响。网络攻防双方存在策略依存关系，博弈收益以特定攻防策略组合的形式出现[21]。因此，无论是攻击方还是防御方，均不能忽略攻防双方的互动决策过程。作为理性的防御方，在防御决策时不仅要考虑自身因素，还应考虑攻击方决策可能带来的影响，实施“基于系统思维的理性换位思考”。

（3）网络攻防双方的关系非合作

网络攻防双方是一对天然矛盾体，相互竞争、相互较量，利益相悖、目标对立且不可调和，构成了博弈模型的对抗性决策主体[22]。网络攻防双方存在非合作对抗关系，不存在共同利益，不可能在决策前相互沟通，不会达成具有约束力的协议，因此，双方不存在任何合作的可能。关系非合作特征决定了网络攻防博弈属于非合作博弈范畴。

（4）网络攻防双方掌握的信息不完备

信息是博弈模型的重要组成元素，能够影响博弈决策。在一定条件下，信息优势能够转化为决策优势。局中人掌握的信息越多，则在博弈过程中占优的可能性越大。由于网络攻防双方存在非合作对抗关系，一方不可能事先将自身决策信息告诉对方，攻击方和防御方一般仅能了解己方信息和部分对方信息，所掌握的信息是有限和不完备的。但是，在动态对抗过程中，一方可利用贝叶斯法则修正先验判断，增强关于对方的认知。

（5）网络攻防态势不断动态演化

从系统论角度理解，安全是动态演化的过程而非静止不变的状态。网络安全是一种涌现属性[23]，涉及微观−宏观效应（micro-macro link）问题，微观层面网络攻防的动态博弈行为，会推动宏观层面网络攻防博弈系统状态的动态演化。网络边界越来越模糊，攻击来源、攻击手段逐渐复杂多样，网络攻击的自动化、智能化、动态化程度越来越高，传统的静态防御思想已经不适合。此外，在网络攻防对抗过程中，网络环境、目标偏好等关键因素可能会发生动态变化。防御方应树立动态、综合的安全防御理念，因人、因时、因势动态改变防御策略。

（6）网络攻防博弈的内因是利益驱动

根据信息安全经济学理论，实施防御策略能够降低预期损失、产生安全收益，但同时需付出人力、物力、计算等资源成本。理性的网络攻击方和防御方都是“经济人”，试图在对抗中选择最大化己方利益的策略。网络安全是相对的而不是绝对的，追求绝对安全不切实际。防御方应树立“适度安全”理念，立足实际情况，根据不同的防御需求和安全能力，通过合理、科学地选择防御策略，在成本和收益之间寻找平衡，增强防御决策的科学性。

1.2 网络攻防博弈模型形式化定义

为构建网络攻防博弈模型、开展网络防御决策分析，本文给出理性局中人假设和资源有限性假设。

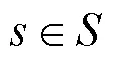
假设2 资源有限性假设：网络攻击方和防御方均受能力、资源和偏好等现实条件约束，可支配的资源、可选取的策略都是有限的而非无限的。

理性局中人假设和资源有限性假设均符合网络攻防对抗实际。其中，理性局中人假设是网络攻防博弈建模的基础前提，资源有限性假设是网络攻防博弈分析的约束条件。

定义1 网络攻防博弈：网络攻防局中人在特定规则约束下，依据所掌握的信息，同时或先后、一次或多次地选择并实施对抗策略，并由此取得各自收益的过程。

（1）攻防局中人

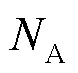
局中人概念在微观层面指网络攻防个体，在宏观层面指攻击方群体和防御方群体。在不完全信息博弈分析中，为方便推理，还需要利用海萨尼转换，引入虚拟局中人“自然”，将不确定性条件下的选择问题转换为风险条件下的选择问题。

（2）攻防策略集

局中人选取的策略可划分为纯策略和混合策略。纯策略指局中人在策略集合中直接选用一种策略；混合策略指局中人以一定的概率组合在策略集中选择若干种策略。

（3）攻防动作集

（4）攻防信息集

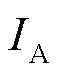
（5）攻防收益集

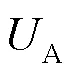
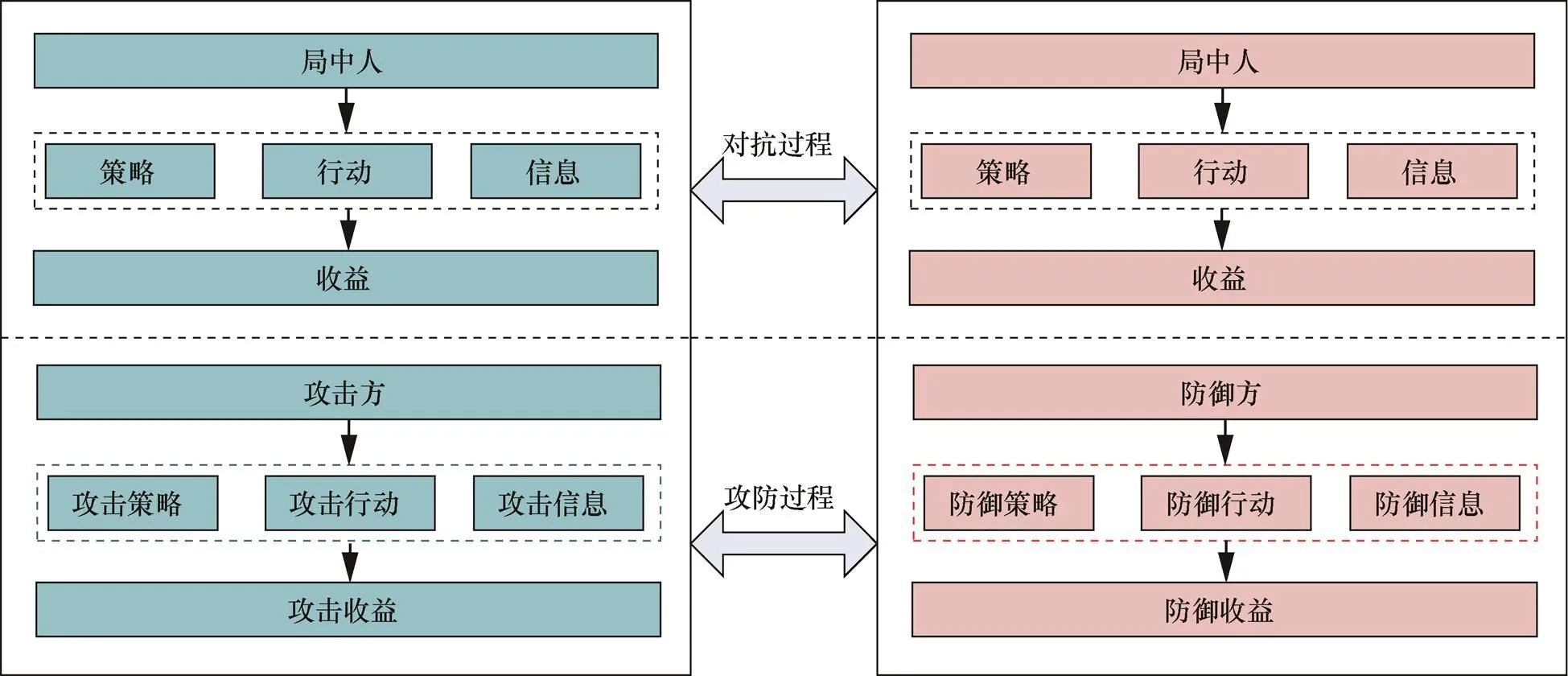
图1 网络攻防过程与博弈模型元素的对应关系

Figure 1 Correspondence between network attack and defense process and elements of game model

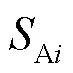
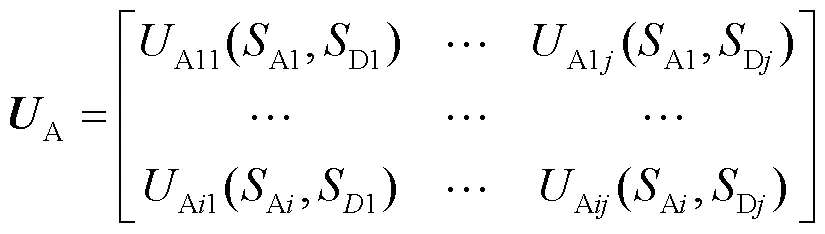
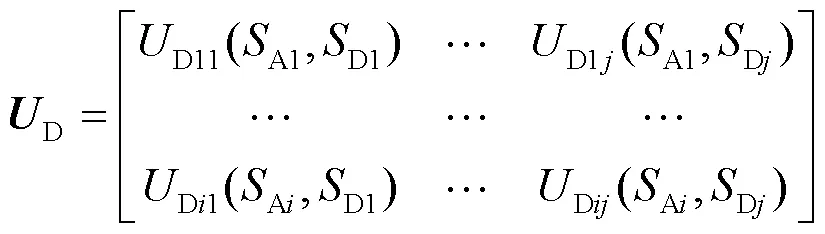
网络攻防过程与博弈模型元素的对应关系如图1所示。

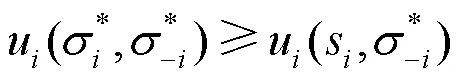
纳什均衡可通俗理解为“给定你的策略，我的策略是我最好的策略；给定我的策略，你的策略是你最好的策略”。根据博弈理论，博弈均衡是所有局中人的最优策略，属于竞赛对抗过程中的稳定局势。在博弈均衡状态下，任何局中人不能通过单方面改变自身策略增加收益。

网络攻防博弈中，攻防局中人数量有限，局中人的策略集合也有限，且网络攻防双方的收益函数均为实值函数。因此，网络攻防博弈存在混合策略下的博弈均衡。纳什均衡的存在性条件对比如表1所示。

表1 纳什均衡的存在性条件

Zhang等[25]和刘景玮等[26]借鉴纳什定理，给出了混合策略概率贝叶斯纳什均衡的存在性证明和博弈均衡的分析求解方法。结合表1给出的纳什均衡存在性条件，可得出网络攻防博弈存在混合策略贝叶斯纳什均衡的结论。

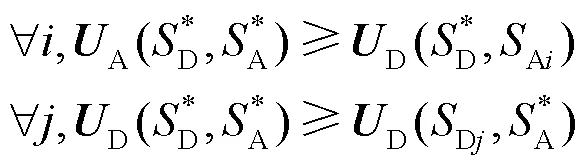
基于攻防博弈模型的网络防御决策方法，将以单个决策者为中心的行为分析，推广到面向攻防对抗的系统推理[27]，其决策过程如图2所示。

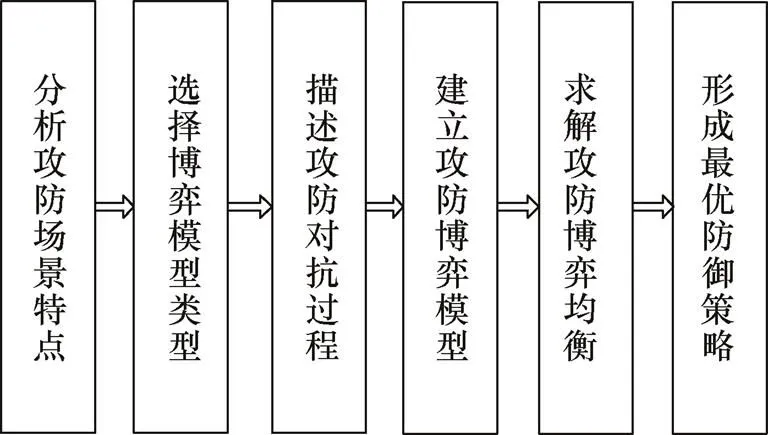
图2 基于攻防博弈模型的网络防御决策过程

Figure 2 General process of network defense decision-making based on attack and defense game model

近年来，研究者基于不同类型的网络攻防博弈，分别提出了适用于不同场景的网络防御决策方法，并在入侵检测规则设定[28-30]、蜜罐策略配置[31-33]、移动目标防御[34-37]、网络空间欺骗防御[14, 38-39]等策略选取方面得到了一定应用。

2 基于不同类型攻防博弈的网络防御决策方法

2.1 基于经典博弈的网络防御决策方法

结合博弈信息和博弈时序两个纬度，经典博弈模型可划分为完全信息静态、完全信息动态、不完全信息静态和不完全信息动态4类[40]。研究者基于以上4类博弈分别提出了不同的网络防御决策方法。

2.1.1 基于完全信息静态博弈的网络防御决策方法

（1）适用场景

完全信息静态博弈是非合作博弈最基本的类型，适用于网络攻防双方能够完全掌握对方信息、同时决策且攻防博弈只进行一次的场景。同时决策指的是逻辑上同时，而非时间上同时。例如，攻防双方在决策时互不掌握对方策略，或者即使掌握对方策略后也不能改变己方所做出的决策，此时，网络攻防双方的决策可看作逻辑上是同时的。

（2）研究思路

基于完全信息静态博弈的网络防御决策方法，一般采用博弈收益矩阵的形式加以推理分析，在纳什均衡解的基础上给出最优防御策略。

（3）相关研究

姜伟等[41]针对网络系统安全测评和最优主动防御问题，提出了网络防御图模型以及一种攻防策略分类及量化方法，给出最优主动防御策略选取方法。Liu等[42]针对网络安全风险评估的问题，提出了基于博弈理论的入侵意图、目标和策略推理的形式化模型。王增光等[43]针对军事信息网络的安全风险评估问题，提出了基于攻防博弈的网络安全风险评估方法，并从安全属性角度量化攻防收益，在风险评估的基础上给出防御策略选取建议。陈永强等[44]针对攻防对抗过程中双方收益不完全对等的问题，提出了网络安全博弈图，结合主机重要度以及防御措施成功率计算攻防收益，给出主动防御策略选取方法。

（4）方法优缺点

基于完全信息静态博弈的网络防御决策方法的优点是博弈模型容易构建、易于推理分析、计算求解相对简单；缺点是博弈模型较为简化、前提假设条件多、适用范围比较窄，无法应用于不完全信息或者攻防过程动态变化的场景。

2.1.2 基于完全信息动态博弈的网络防御决策方法

（1）适用场景

静态博弈和动态博弈的区别在于决策是否具有序贯性。完全信息动态博弈适用于攻防双方能够完全掌握对方信息、攻防决策具有先后顺序、后行为者能够观察先行为者策略，攻防对抗过程具有动态性特点的场景。

（2）研究思路

基于完全信息动态博弈的网络防御决策方法，一般采用博弈扩展式（攻防博弈树）的形式加以推理分析，在子博弈完美纳什均衡解的基础上给出最优防御策略。

（3）相关研究

Agah等[45]针对无线传感网中DoS攻击的最优防御策略选取问题，建立了入侵检测系统与节点间的重复博弈模型，设计了一种可识别恶意节点的通信协议，给出了最优策略选取方法。林旺群等[46]针对攻击方意图和策略动态变化情况下的最优防御策略选取问题，通过引入虚拟节点将网络攻防图转化为攻防博弈树，给出防御策略选取算法。孙骞等[47]针对多路径组合攻击环境下最优防御策略的选取问题，定义了攻击成本、惩罚因子、防御代价，针对多路径组合攻防特点，建立了攻防博弈模型，给出最优防御策略选取方法。

（4）方法优缺点

基于完全信息动态博弈的网络防御决策方法的优点是考虑到攻防对抗的持续性和动态性，可以应用于攻击方意图、攻击手段、攻击路径、攻击策略等发生变化时的网络攻防场景；缺点是“完全信息”的前提条件要求较为苛刻，造成决策方法适用的网络攻防场景有限。

2.1.3 基于不完全信息静态博弈的网络防御决策方法

（1）适用场景

不完全信息静态博弈又称静态贝叶斯博弈，适用于网络攻防对抗中，攻防局中人决策行为在逻辑上同时发生，且任意一方不能完全获取另一方决策和收益等关键信息的场景。不完全信息静态博弈，引入了类型的概念。类型属于私人信息，局中人可利用静态贝叶斯法则推断。

（2）研究思路

基于不完全信息静态博弈的网络防御决策方法，一般采用海萨尼转换，引入虚拟局中人“自然”的形式加以推理分析，在贝叶斯纳什均衡解的基础上给出最优防御策略。

（3）相关研究

王晋东等[48]针对防御决策方法中未考虑攻击方的类型、防御方的反击行为等问题，建立网络攻防博弈模型，结合攻击者类型、防御者反击行为和攻击成功率改进收益量化方法，给出了主动防御设计策略选取方法。陈永强等[49]针对网络攻防过程中攻防双方无法获取对方信息，以及无法对双方损益做出准确判定的问题，建立了模糊静态贝叶斯博弈模型，引入三角模糊数描述攻防双方的效用函数，设计了主动防御策略选取方法。余定坤等[50]针对防御决策方法仅考虑攻击方类型未考虑防御方类型，策略选取可操作性差等问题，将攻防双方均划分为多种类型，认为攻击方混合策略是防御方对攻击方可能采取行动的可信预测，给出了最优混合防御策略选取方法。刘玉岭等[51]针对蠕虫病毒的最优防御策略选取问题，构建了基于静态贝叶斯的绩效评估模型，提出了基于灰色多属性理论的防护策略绩效评估方法，设计了最优防御策略选取方法。

（4）方法优缺点

基于不完全信息静态博弈的网络防御决策方法的优点是考虑到攻防双方信息掌握的不完全性，相对于完全信息假设，更加符合网络攻防的实际特点；缺点是该方法假设攻防局中人只进行一次博弈，无法应用于多次对抗的场景。

2.1.4 基于不完全信息动态博弈的网络防御决策方法

（1）适用场景

不完全信息动态博弈又称动态贝叶斯博弈，适用于网络攻防对抗中，攻防局中人行动上有先后顺序，后行为者能够观察先行为者的行动并获取有关先行为者信息的场景。

（2）研究思路

基于不完全信息动态博弈的网络防御决策方法，一般采用海萨尼转换的方法，利用博弈树加以分析推理，在完美贝叶斯纳什均衡解的基础上给出最优防御策略。其中，信号博弈是具有信息传递机制的不完全信息动态博弈。它通过信号传递描述局中人策略交互过程，在网络主动防御[52-53]、网络欺骗防御[54]等领域得到了一定应用。

（3）相关研究

胡永进等[55-56]针对网络欺骗防御中最优策略选取问题，构建了多阶段网络欺骗博弈模型，考虑网络欺骗信号衰减作用，设计了最优网络欺骗防御策略选取算法。Yang等[57]针对物联网环境下最优防御策略选取问题，结合物联网特点，提出了一种多阶段网络攻防博弈模型，设计了防御策略选取算法。Chen等[58]针对工业控制系统防御钓鱼叉式攻击的最优策略选取问题，提出了一种多阶段攻防信号博弈模型，采用符号变量量化攻防收益，给出了最优策略选取方法，分析了影响博弈结果的关键因素。Liu等[59]针对基于信号博弈的网络防御决策研究大多采用单向信号传递机制问题，分析了攻防对抗中的双向信号传递机制，提出了网络攻防双向信号博弈模型，给出最优欺骗防御策略选取方法，分析了欺骗信号作用机理。Aydeger等[60]针对Stealthy Link Flooding Attack攻击的防御策略选取问题，建立了网络攻防移动目标防御信号博弈模型，通过求解博弈均衡，得出最佳防御策略，有效缓解Stealthy Link Flooding Attack攻击。Pawlick等[61-62]针对网络欺骗防御中最优防御策略选取问题，建立了网络攻防信号博弈模型，在分析博弈均衡的基础上，得出最优欺骗防御策略。

（4）方法优缺点

基于不完全信息动态博弈的网络防御决策方法的优点是考虑了网络攻防对抗的动态性和持续性，能够刻画具有多阶段、多回合特点的对抗过程[63]；缺点是网络攻防建模工作量大，博弈均衡分析求解相对复杂。

2.2 基于新型博弈类型的网络防御决策方法

近年来，演化博弈、微分博弈、时间博弈和随机博弈等新型博弈类型，越来越多地应用到网络防御决策方法研究中。

2.2.1 基于演化博弈的网络防御决策方法

（1）适用场景

经典博弈理论一般假设局中人完全理性，具有无限的信息处理和计算能力，并且在决策过程不会出现失误、不受别人影响。然而在网络攻防对抗中该假设很难满足，攻防双方的理性都是有限而非完全的。演化博弈以随时间动态演化的群体为研究对象，突破了局中人完全理性限制[64]，将博弈均衡视为局中人通过学习进化逐步寻优的结果，能够更加准确地刻画群体策略演化过程。

（2）研究思路

演化博弈过程中，在学习机制的驱动和博弈收益差值的影响下，优势策略会在局中人群体中逐步扩散，并最终形成演化稳定策略（ESS，evolutionarily stale strategy），局中人依据演化稳定策略实施防御决策。

（3）相关研究

Alabdel等[65]针对云存储环境下防御APT攻击的最优策略选取问题，利用演化博弈描述APT攻击攻防行为，采用复制动态学习机制建立网络攻防博弈模型，分析了演化稳定策略。黄健明等[66-68]针对同一博弈群体之间存在策略依存性时最优防御策略选取问题，引入激励系数改进复制动态学习机制，完善复制动态速率计算方法，提出了最优防御策略选取算法。Shi等[69]针对蜜罐诱骗防御策略选取问题，构建了由防御方、攻击方和合法用户组成的三方博弈模型，通过复制动态方程得出演化稳定策略，得出最优诱骗策略。张恒巍等[70]针对攻防双方的有限理性限制条件和攻防过程的动态变化特征问题，将演化博弈与Markov决策模型相结合，构建多阶段Markov攻防演化博弈模型。Hu等[71]针对动态对抗网络中最优防御策略选取问题，将攻防双方对策略收益的不确定性转化为对类型的不确定性，利用选择强度因子描述噪声，改进了复制动态学习机制，设计了最优防御策略选取算法。Liu等[72]针对网络攻防对抗中，防御方学习能力范围有限的实际问题，提出了基于演化网络博弈的网络防御决策方法。防御方依据学习能力建立学习对象集，利用费米函数计算策略转移概率，提出了最优防御策略选取方法。

（4）方法优缺点

基于演化博弈的网络防御决策方法的优点是突破了局中人完全理性限制，适用于群体网络攻防场景，缺点是复制动态学习机制假设全体局中人之间能够以均匀混合、完全接触的方式进行交互，不适用于异质群体网络攻防场景。研究者正在从不同的角度对复制动态学习机制进行研究和改进，使博弈模型更加符合网络攻防对抗实际。

2.2.2 基于微分博弈的网络防御决策方法

（1）适用场景

微分博弈是时间实时变化情况下描述冲突对抗中连续控制过程的理论方法。它将离散的博弈过程扩展到连续时间，局中人可以实时改变控制策略。微分博弈适用于描述具有连续、实时、动态特征的攻防对抗场景。

（2）研究思路

基于微分博弈的网络防御决策方法研究过程为：构建网络攻防微分博弈模型，设计攻防决策控制函数和收益积分函数，在求解鞍点控制策略的基础上给出最优防御策略。

（3）相关研究

张恒巍等[20, 73-74]针对快速变化和连续对抗的网络环境下的网络防御决策问题，借鉴传染病动力学理论，提出安全状态演化模型分析网络系统安全状态的变化过程。黄世锐等[75]针对网络攻防连续对抗、实时变化环境下的网络安全威胁预警问题，借鉴传染病动力学分析安全威胁传播过程，构造攻防界栅以及捕获区和躲避区，引入多维欧氏距离度量威胁程度。孙岩等[76]针对移动目标防御最优策略研究大多采用经典单/多阶段博弈和Markov博弈模型，无法在连续实时网络攻防对抗中进行灵活决策问题，在研究节点级传染病模型与微分博弈理论的基础上，提出了一种移动目标防御微分博弈模型，对网络空间重要节点构造安全状态演化方程与攻防收益目标函数，并设计开环纳什均衡求解算法以得出最优防御策略。

（4）方法优缺点

基于微分博弈的网络防御决策方法的优点是适用于连续、实时、动态的网络攻防场景；缺点是网络攻防微分博弈模型的构建、决策控制函数的分析和鞍点控制策略的求解难度大。

2.2.3 基于时间博弈的网络防御决策方法

（1）适用场景

时间博弈由美国RSA实验室的Dijk提出，旨在建模和分析APT攻击和防御过程。网络攻防时间博弈由攻击方局中人、防御方局中人和公共资源3部分组成，攻防局中人共同争夺对公共资源的控制权。

（2）研究思路

基于时间博弈的网络防御决策方法研究，一般通过对公共资源的控制时间刻画攻防收益。FlipIt博弈及其扩展版本是时间博弈的主要研究方向。

（3）相关研究

Dijk等[77]针对APT攻击场景中，最优防御策略选取问题，首次提出FlipIt博弈模型，并将其应用于网络攻防博弈分析，给出了最优防御策略选取方法。丁绍虎等[78-79]针对APT攻击场景中，异构性条件下的拟态防御动态策略评估问题，提出了一种改进的FlipIt博弈模型M-FlipIt，对拟态防御动态策略进行评估。Laszka等[80]针对由多个目标资源组成系统的最优防御策略选取问题，提出了FlipItThem模型，引入两种控制模型（and模型和or模型），形式化了博弈的目标和策略。谭晶磊等[81-82]针对移动目标防御场景下最优防御策略选取问题，构建了移动目标攻防策略集，利用时间博弈刻画了单阶段移动目标防御过程的动态性，采用马尔可夫过程描述移动目标防御状态转化的随机性。Miura等[83]针对恶意软件的最优防御策略选取问题，结合传染病模型建立了FlipIt博弈模型，攻击方和防御方争夺主机的计算资源，基于纳什均衡得到最优响应，生成最优防御策略。Merlevede等[84]针对时间博弈过程中未来收益折现问题，引入时间折扣因子优化攻防效用函数计算方法，建立了Fliplt模型，允许收益和成本随时间进行指数折扣。Pawlick等[85]针对物联网环境下应对APT攻击的最优防御策略问题，建立了云服务管理员和攻击方之间的信号博弈和Fliplt模型，使用信号博弈均衡作为Fliplt模型的激励机制，Fliplt模型影响信号博弈中先验概率。

（4）方法优缺点

基于时间博弈的网络防御决策方法的优点是模型的针对性较强，适用于描述对公共资源控制权交替变换的场景，如APT攻击与防御、移动目标防御中的攻击面转移等；缺点是模型的适应性和迁移性差，应用范围相对狭窄。

2.2.4 基于随机博弈的网络防御决策方法

（1）适用场景

随机博弈是博弈论与马尔可夫决策过程（Markov decision process，MDP）结合的产物，适用于描述具有多状态、随机性特点的系统状态转移过程。

（2）研究思路

基于随机博弈的网络防御决策方法研究，一般采用马尔可夫决策过程分析网络攻防行为，建立网络攻防对抗随机博弈模型，在求解博弈均衡解的基础上给出最优防御策略。

（3）相关研究

Lye等[86]针对网络攻防博弈中攻击行为预测和最优防御策略选取的问题，建立了五元组网络攻防博弈模型，结合马尔可夫链预测网络攻击行为，给出了最优防御策略选取方法。王元卓等[87]针对网络攻防过程的实验推演问题，采用随机博弈模型设计网络攻防实验整体架构，提出了由网络连接关系、脆弱性信息等输入数据到网络攻防博弈的快速建模方法。Wang等[88]针对开放环境下网络生存性问题，将网络生存性抽象为网络攻击方、防御方和正常用户之间的动态博弈过程，建立了网络生存性随机博弈模型，提出了网络生存性分析算法。张红旗等[89]针对随机博弈大多以完全信息假设为前提的问题，将防御方对攻击方收益的不确定性转化为对其类型的不确定性，引入Q-learning算法，设计了能够在线学习的防御决策算法。杨峻楠等[90-91]针对随机博弈大多采用完全理性的假设问题，分析有限理性对攻防随机博弈的影响，提出了一种基于攻防图的网络状态与攻防动作提取方法，引入WoLF-PHC算法提出了具有在线学习能力的防御决策算法。

（4）方法优缺点

基于随机博弈的网络防御决策方法研究的优点是能够刻画出网络攻防的随机性和动态性；缺点是随机博弈模型中，网络安全状态转移概率难以确定，造成博弈均衡难以求解，大多由专家经验或历史数据给出转移概率，存在一定的主观性。

3 总结与展望

3.1 总结

（1）发展过程

基于攻防博弈的网络防御决策方法研究，经历了由静态到动态、由完全信息到不完全信息、由完全理性到不完全理性的发展过程。在研究初始阶段，为方便分析、简化计算、易于理解，研究者大多基于静态、完全信息、完全理性等假设，针对特定的网络攻防场景，分别建立相对简化的网络攻防博弈模型，提出网络防御决策方法。但是，随着网络攻防策略越来越多样、网络攻防场景越来越复杂，对网络攻防博弈建模分析的准确性要求越来越高。近年来，相关学者逐渐倾向于采用基于动态、不完全信息、非完全理性等博弈理论，建立更加符合网络攻防实际的博弈模型，提升网络防御决策方法的应用价值。

（2）优势特点

博弈论为描述网络攻防矛盾提供了一种数学框架。通过建立网络攻防博弈模型，运用数学方法量化攻防收益、计算博弈均衡，能够形成对攻击方策略的可信、有效预测，得出防御方的最优策略，从而在网络攻防对抗中掌握主动、避免被动。同时，博弈理论能够促使决策者转换思维方式，从攻防对抗角度理解和认识网络防御决策问题。防御方在决策时不仅要考虑自身因素，还要关注网络攻防双方的目标偏好、策略依存关系、信息掌握程度和动态演化趋势等内容，树立起“适度安全、动态安全”理念，增强对网络安全本质的认知，形成正确的网络安全观。

（3）面临问题

现有基于攻防博弈的网络防御决策方法在具体应用中可能会面临3个问题。一是博弈建模考虑因素与模型复杂度的关系问题。博弈建模过程中若考虑因素越少，则博弈模型越简化，所得决策方法可能脱离网络攻防实际；若考虑因素越多，网络攻防博弈推理分析越复杂，均衡求解的计算量越大，越难以满足网络防御决策的实时性要求。二是博弈推理对信息和数据的依赖性问题。网络攻防博弈分析推理高度依赖于攻防信息和历史数据；但是，网络攻防信息和历史数据存在来源多样、格式异构、可信性不强等问题，在一定限度上影响了博弈分析推理过程。三是博弈模型的泛化性和迁移性问题。博弈建模大多针对特定的网络攻防场景，所建博弈模型的泛化性和迁移性较差，限制了网络防御决策方法的推广应用。

3.2 展望

（1）规范策略的描述机制

策略是博弈模型的重要组成要素。网络攻防策略描述机制能够对博弈建模和推理分析产生重要影响。攻防策略空间大小直接影响博弈模型的计算复杂度，从而影响网络防御决策的速度和质量。例如，若攻防策略空间过于简单，虽然有利于降低决策难度，但影响网络防御决策方法的实用性；若攻防策略空间过于复杂，则会增加博弈分析的复杂度和均衡求解的计算量，从而影响网络防御决策的时效性。

网络防御决策方法大多由研究者根据自身建模需要对攻防策略进行描述，主观性强、随意性大、适用性差。同时，研究者基于不同的策略描述机制所提出的网络防御决策方法，相互之间难以验证和对比分析。因此，建立统一的网络攻防策略库和权威、合理的策略描述机制，为研究者提供公用的策略实例，将是非常有意义的研究工作。

（2）优化收益的计算方法

网络攻防收益量化是计算的前提。网络攻防博弈存在一定的不确定性和模糊性，使得难以用精确数值表示网络攻防收益。特别是，系统损失、成本投入、资产重要程度等价值可能随着用户偏好、系统环境的不同而变化，这给攻防收益量化造成了困难。因此，一般应将网络攻防收益量化为相对的、无量纲值，数值的大小仅表示程度，不具备实际的物理含义。

网络攻防收益计算是博弈均衡求解的基础。现有基于攻防博弈的网络防御决策方法研究中，攻防收益计算较多采用回报直接减去成本的方法，但方法的准确性和权威性仍有待讨论。尤其是网络攻防动态博弈的收益计算涉及现实收益和未来收益，未来收益还面临着折现问题。部分学者采用折现因子将未来收益折现成现实收益，但这种方法简单粗暴。下一步的研究重点是：从多属性角度建立网络攻防收益量化评估准则，采用加权方法计算网络攻防收益，增强收益计算方法的普适性。

（3）与其他技术相互融合

将博弈理论与其他网络安全技术相互融合是网络防御决策方法的重点研究方向，主要有3个方面。一是与人工智能相结合。通过引入强化学习算法求解博弈均衡，防御方能够以在线学习方式逐步逼近最优策略，缩短决策周期，形成网络防御决策的时间优势。二是与网络安全态势感知和威胁情报相结合。通过准确感知网络攻防态势，获取攻击方情报信息，增强博弈推理分析的准确性，形成网络防御决策的信息优势。三是与主动防御技术结合。移动目标防御、拟态防御、欺骗防御等新型主动防御技术发展如火如荼，将基于攻防博弈的网络防御决策方法与主动防御技术相结合，可从技术层和策略层共同增强防御效果。

4 结束语

科学有效的决策方法是增强网络防御效能的关键。基于攻防博弈开展网络防御决策方法的研究是网络安全领域的前沿热点问题。本文重点梳理分析了基于完全信息静态博弈、完全信息动态博弈、不完全信息静态博弈、不完全信息动态博弈、演化博弈、微分博弈、时间博弈和随机博弈8种博弈类型的网络防御决策方法的适用场景、研究思路、相关研究和优缺点。但是，如何对不同类型博弈模型进行融合创新，提出适用于复杂攻防场景的网络防御决策方法，并开展方法的有效性验证，以及如何迁移应用到真实网络攻防过程中，仍然是值得研究的问题。

[1] LI X T. Decision making of optimal investment in information security for complementary enterprises based on game theory[J]. Technology Analysis & Strategic Management, 2021, 33(7): 755-769.

[2] AGGARWAL P, MOISAN F, GONZALEZ C, et al. Learning about the effects of alert uncertainty in attack and defend decisions via cognitive modeling[J]. Human Factors: the Journal of the Human Factors and Ergonomics Society, 2020: 001872082094542.

[3] SHEKARIAN E, FLAPPER S D. Analyzing the structure of closed-loop supply chains: a game theory perspective[J]. Sustainability, 2021, 13(3): 1397.

[4] XIAO Y, PENG Q, XU W T, et al. Production-use water pricing and corporate water use in China: an evolutionary game theory model[J]. Mathematical Problems in Engineering, 2021, 2021: 6622064.

[5] CHEUNG K F, BELL M G H. Attacker-defender model against quantal response adversaries for cyber security in logistics management: an introductory study[J]. European Journal of Operational Research, 2021, 291(2): 471-481.

[6] ALSABBAGH A, WU B, MA C B. Distributed electric vehicles charging management considering time anxiety and customer behaviors[J]. IEEE Transactions on Industrial Informatics, 2021, 17(4): 2422-2431.

[7] GARCIA E, CASBEER D W, PACHTER M. Design and analysis of state-feedback optimal strategies for the differential game of active defense[J]. IEEE Transactions on Automatic Control, 2018, 64(2): 553-568.

[8] 张焕国, 杜瑞颖. 网络空间安全学科简论[J]. 网络与信息安全学报, 2019, 5(3): 4-18.

ZHANG H G, DU R Y. Introduction to cyberspace security discipline[J]. Chinese Journal of Network and Information Security, 2019, 5(3): 4-18.

[9] LIANG X N, XIAO Y. Game theory for network security[J]. IEEE Communications Surveys & Tutorials, 2013, 15(1): 472-486.

[10] WANG Y, WANG Y J, LIU J, et al. A survey of game theoretic methods for cyber security[C]//Proceedings of 2016 IEEE First International Conference on Data Science in Cyberspace. Piscataway: IEEE Press, 2016: 631-636.

[11] MANSHAEI M H, ZHU Q Y, ALPCAN T, et al. Game theory meets network security and privacy[J]. ACM Computing Surveys, 2013, 45(3): 1-39.

[12] ZHU Q Y, RASS S. Game theory meets network security: a tutorial[C]//Proceedings of the 2018 ACM SIGSAC Conference on Computer and Communications Security. 2018: 2163-2165.

[13] ETESAMI S R, BAŞAR T. Dynamic games in cyber-physical security: an overview[J]. Dynamic Games and Applications, 2019, 9(4): 884-913.

[14] YE D Y, ZHU T Q, SHEN S, et al. A differentially private game theoretic approach for deceiving cyber adversaries[J]. IEEE Transactions on Information Forensics and Security, 2021, 16: 569-584.

[15] DAHIYA A, GUPTA B B. A reputation score policy and Bayesian game theory based incentivized mechanism for DDoS attacks mitigation and cyber defense[J]. Future Generation Computer Systems, 2021, 117: 193-204.

[16] DO C T, TRAN N H, HONG C, et al. Game theory for cyber security and privacy[J]. ACM Computing Surveys, 2018, 50(2): 1-37.

[17] KUMAR B, BHUYAN B. Using game theory to model DoS attack and defence[J]. Sādhanā, 2019, 44(12): 1-12.

[18] MERRICK K, HARDHIENATA M, SHAFI K, et al. A survey of game theoretic approaches to modelling decision-making in information warfare scenarios[J]. Future Internet, 2016, 8(3): 34.

[19] PENG R, WU D, SUN M Y, et al. An attack-defense game on interdependent networks[J]. Journal of the Operational Research Society, 2021, 72(10): 2331-2341.

[20] ZHANG H W, JIANG L, HUANG S R, et al. Attack-defense differential game model for network defense strategy selection[J]. IEEE Access, 2019, 7: 50618-50629.

[21] 朱建明, 王秦. 基于博弈论的网络空间安全若干问题分析[J]. 网络与信息安全学报, 2015, 1(1): 43-49.

ZHU J M, WANG Q. Analysis of cyberspace security based on game theory[J]. Chinese Journal of Network and Information Security, 2015, 1(1): 43-49.

[22] JIANG W, FANG B X, ZHANG H L, et al. Optimal network security strengthening using attack-defense game model[C]//Proceedings of 2009 Sixth International Conference on Information Technology: New Generations. Piscataway: IEEE Press, 2009: 475-480.

[23] 屈蕾蕾, 肖若瑾, 石文昌, 等. 涌现视角下的网络空间安全挑战[J]. 计算机研究与发展, 2020, 57(4): 803-823.

QU L L, XIAO R J, SHI W C, et al. Cybersecurity challenges from the perspective of emergence[J]. Journal of Computer Research and Development, 2020, 57(4): 803-823.

[24] DUFWENBERG M. Game theory[J]. WIREs Cognitive Science, 2011, 2(2): 167-173.

[25] ZHANG H W, LI T, WANG J D, et al. Optimal active defence using dynamic multi-stage signalling game[J]. China Communications, 2015, 12(S2): 114-122.

[26] 刘景玮, 刘京菊, 陆余良, 等. 基于网络攻防博弈模型的最优防御策略选取方法[J]. 计算机科学, 2018, 45(6): 117-123.

LIU J W, LIU J J, LU Y L, et al. Optimal defense strategy selection method based on network attack-defense game model[J]. Computer Science, 2018, 45(6): 117-123.

[27] 刘小虎, 张恒巍, 张玉臣, 等. 基于博弈模型与NetLogo仿真的网络攻防态势研究[J]. 系统仿真学报, 2020, 32(10): 1918-1926.

LIU X H, ZHANG H W, ZHANG Y C, et al. Research on network attack and defense situation based on game theory model and NetLogo simulation[J]. Journal of System Simulation, 2020, 32(10): 1918-1926.

[28] GILL K S, SAXENA S, SHARMA A. GTM-CSec: game theoretic model for cloud security based on IDS and honeypot[J]. Computers & Security, 2020, 92: 101732.

[29] MISHRA B, SMIRNOVA I. Optimal configuration of intrusion detection systems[J]. Information Technology and Management, 2021, 22(4): 231-244.

[30] WEILL C, OLIVEREAU A, ZEGHLACHE D, et al. Configuration of the Detection Function in a Distributed IDS Using Game Theory[M]//2020 23rd Conference on Innovation In Clouds, Internet And Networks And Workshops. New York; IEEE. 2020. 210-215.

[31] DIAMANTOULAKIS P, DALAMAGKAS C, RADOGLOU-GRAMMATIKIS P, et al. Game theoretic honeypot deployment in smart grid[J]. Sensors (Basel, Switzerland), 2020, 20(15): 4199.

[32] TIAN W, JI X P, LIU W W, et al. Honeypot game-theoretical model for defending against APT attacks with limited resources in cyber-physical systems[J]. ETRI Journal, 2019, 41(5): 585-598.

[33] LI Y, SHI L Y, FENG H J. A game-theoretic analysis for distributed honeypots[J]. Future Internet, 2019, 11(3): 65.

[34] SAMIR M, AZAB M, SAMIR E. SD-CPC: SDN controller placement camouflage based on stochastic game for moving-target defense[J]. Computer Communications, 2021, 168: 75-92.

[35] WANG S L, SHI H W, HU Q, et al. Moving target defense for Internet of Things based on the zero-determinant theory[J]. IEEE Internet of Things Journal, 2020, 7(1): 661-668.

[36] WRIGHT M, VENKATESAN S, ALBANESE M, et al. Moving target defense against DDoS attacks: an empirical game-theoretic analysis[C]// Proceedings of the 2016 ACM Workshop on Moving Target Defense. 2016: 93-104.

[37] CAI G L, WANG B S, XING Q Q. Game theoretic analysis for the mechanism of moving target defense[J]. Frontiers of Information Technology & Electronic Engineering, 2017, 18(12): 2017-2034.

[38] PAWLICK J, COLBERT E, ZHU Q Y. Analysis of leaky deception for network security using signaling games with evidence[R. New York University, 2018.

[39] ZENG C Y, REN B A, LIU H F, et al. Applying the Bayesian stackelberg active deception game for securing infrastructure networks[J]. Entropy, 2019, 21(9): 909.

[40] 张维迎. 博弈论与信息经济学[M]. 上海: 格致出版社, 2012.

ZHANG W Y. Game theory and information economics[M]. Shanghai: Gezhi publishing house, 2012.

[41] 姜伟, 方滨兴, 田志宏, 等. 基于攻防博弈模型的网络安全测评和最优主动防御[J]. 计算机学报, 2009, 32(4): 817-827.

JIANG W, FANG B X, TIAN Z H, et al. Evaluating network security and optimal active defense based on attack-defense game model[J]. Chinese Journal of Computers, 2009, 32(4): 817-827.

[42] LIU P, ZANG W Y, YU M. Incentive-based modeling and inference of attacker intent, objectives, and strategies[J]. ACM Transactions on Information and System Security, 2005, 8(1): 78-118.

[43] 王增光, 卢昱, 李玺. 基于攻防博弈的军事信息网络安全风险评估[J]. 军事运筹与系统工程, 2019, 33(2): 35-40, 47.

WANG Z G, LU Y, LI X. Military information network security risk assessment based on attack defense game[J]. Military Operations Research and Systems Engineering, 2019, 33(2): 35-40, 47.

[44] 陈永强, 付钰, 吴晓平. 基于非零和攻防博弈模型的主动防御策略选取方法[J]. 计算机应用, 2013, 33(5): 1347-1349, 1352.

CHEN Y Q, FU Y, WU X P. Active defense strategy selection based on non-zero-sum attack-defense game model[J]. Journal of Computer Applications, 2013, 33(5): 1347-1349, 1352.

[45] AGAH A, DAS S K. Preventing DoS attacks in wireless sensor networks: a repeated game theory approach[J]. International Journal of Network Security, 2007, 5(2): 145-153.

[46] 林旺群, 王慧, 刘家红, 等. 基于非合作动态博弈的网络安全主动防御技术研究[J]. 计算机研究与发展, 2011, 48(2): 306-316. LIN W Q, WANG H, LIU J H, et al. Research on active defense technology in network security based on non-cooperative dynamic game theory[J]. Journal of Computer Research and Development, 2011, 48(2): 306-316.

[47] 孙骞, 高岭, 刘涛, 等. 基于非零和博弈的多路径组合攻击防御决策方法[J]. 西北大学学报(自然科学版), 2019, 49(3): 343-350. SUN Q, GAO L, LIU T, et al. Defense decision-making method for multi-path combined attack based on non-zero-sum game[J]. Journal of Northwest University (Natural Science Edition), 2019, 49(3): 343-350.

[48] 王晋东, 余定坤, 张恒巍, 等. 静态贝叶斯博弈主动防御策略选取方法[J]. 西安电子科技大学学报, 2016, 43(1): 144-150.

WANG J D, YU D K, ZHANG H W, et al. Active defense strategy selection based on the static Bayesian game[J]. Journal of Xidian University, 2016, 43(1): 144-150.

[49] 陈永强, 吴晓平, 付钰, 等. 基于模糊静态贝叶斯博弈的网络主动防御策略选取[J]. 计算机应用研究, 2015, 32(3): 887-889, 899.

CHEN Y Q, WU X P, FU Y, et al. Active defense strategy selection of network based on fuzzy static Bayesian game model[J]. Application Research of Computers, 2015, 32(3): 887-889, 899.

[50] 余定坤, 王晋东, 张恒巍, 等. 基于静态贝叶斯博弈的风险评估方法研究[J]. 计算机工程与科学, 2015, 37(6): 1079-1086. YU D K, WANG J D, ZHANG H W, et al. Risk assessment selection based on static Bayesian game[J]. Computer Engineering & Science, 2015, 37(6): 1079-1086.

[51] 刘玉岭, 冯登国, 吴丽辉, 等. 基于静态贝叶斯博弈的蠕虫攻防策略绩效评估[J]. 软件学报, 2012, 23(3): 712-723.

LIU Y L, FENG D G, WU L H, et al. Performance evaluation of worm attack and defense strategies based on static Bayesian game[J]. Journal of Software, 2012, 23(3): 712-723.

[52] 黄万伟, 袁博, 王苏南, 等. 基于非零和信号博弈的主动防御模型[J]. 郑州大学学报(工学版), 2022, 43(1): 90-96.

HUANG W W, YUAN B, WANG S N, et al. Proactive defense model based on non-zero-sum signal game[J]. Journal of Zhengzhou University (Engineering Science), 2022, 43(1): 90-96.

[53] 王增光, 卢昱, 李玺. 多阶段信号博弈的装备保障信息网络主动防御[J]. 火力与指挥控制, 2020, 45(12): 142-148. WANG Z G, LU Y, LI X. Research on active defense of equipment support information network based on multi-stage signaling game[J]. Fire Control & Command Control, 2020, 45(12): 142-148.

[54] 李凌书, 邬江兴, 曾威, 等. 容器云中基于信号博弈的容器迁移与蜜罐部署策略[J]. 网络与信息安全学报, 2022, 8.

LI L S, WU J X, ZENG W, et al. Strategy of container migration and honeypot deployment based on signal game in cloud environment[J]. Chinese Journal of Network and Information Security, 2022, 8.

[55] 胡永进, 马骏, 郭渊博, 等. 基于多阶段网络欺骗博弈的主动防御研究[J]. 通信学报, 2020, 41(8): 32-42. HU Y J, MA J, GUO Y B, et al. Research on active defense based on multi-stage cyber deception game[J]. Journal on Communications, 2020, 41(8): 32-42.

[56] 胡永进, 马骏, 郭渊博. 基于博弈论的网络欺骗研究[J]. 通信学报, 2018, 39(S2): 9-18.

HU Y J, MA J, GUO Y B. Research on cyber deception based on game theory[J]. Journal on Communications, 2018, 39(S2): 9-18.

[57] YANG Y, CHE B C, ZENG Y, et al. MAIAD: a multistage asymmetric information attack and defense model based on evolutionary game theory[J]. Symmetry, 2019, 11(2): 215.

[58] CHEN X Y, LIU X T, ZHANG L, et al. Optimal defense strategy selection for spear-phishing attack based on a multistage signaling game[J]. IEEE Access, 2019, 7: 19907-19921.

[59] LIU X H, ZHANG H W, ZHANG Y C, et al. Active defense strategy selection method based on two-way signaling game[J]. Security and Communication Networks, 2019, 2019: 1362964.

[60] AYDEGER A, MANSHAEI M H, RAHMAN M A, et al. Strategic defense against stealthy link flooding attacks: a signaling game approach[J]. IEEE Transactions on Network Science and Engineering, 2021, 8(1): 751-764.

[61] PAWLICK J, COLBERT E, ZHU Q Y. Modeling and analysis of leaky deception using signaling games with evidence[J]. IEEE Transactions on Information Forensics and Security, 2019, 14(7): 1871-1886.

[62] PAWLICK J, ZHU Q Y. Deception by design: evidence-based signaling games for network defense[EB/OL]. 2015: arXiv: 1503.05458[cs.CR].

[63] 蒋侣, 张恒巍, 王晋东. 基于多阶段Markov信号博弈的移动目标防御最优决策方法[J]. 电子学报, 2021, 49(3): 527-535.

JIANG L, ZHANG H W, WANG J D. A Markov signaling game-theoretic approach to moving target defense strategy selection[J]. Acta Electronica Sinica, 2021, 49(3): 527-535.

[64] 张青青, 汤红波, 游伟, 等. 基于演化博弈的NFV拟态防御架构动态调度策略[J]. 计算机工程, 2021.

ZHANG Q Q, TANG H B, YOU W, et al. Dynamic scheduling strategies of NFV mimic defense architecture based on evolutionary game[J]. Computer Engineering, 2021.

[65] ALABDEL ABASS A A, XIAO L, MANDAYAM N B, et al. Evolutionary game theoretic analysis of advanced persistent threats against cloud storage[J]. IEEE Access, 2017, 5: 8482-8491.

[66] 黄健明, 张恒巍, 王晋东, 等. 基于攻防演化博弈模型的防御策略选取方法[J]. 通信学报, 2017, 38(1): 168-176.

HUANG J M, ZHANG H W, WANG J D, et al. Defense strategies selection based on attack-defense evolutionary game model[J]. Journal on Communications, 2017, 38(1): 168-176.

[67] 黄健明, 张恒巍. 基于改进复制动态演化博弈模型的最优防御策略选取[J]. 通信学报, 2018, 39(1): 170-182.

HUANG J M, ZHANG H W. Improving replicator dynamic evolutionary game model for selecting optimal defense strategies[J]. Journal on Communications, 2018, 39(1): 170-182.

[68] HUANG J M, WANG J D, ZHANG H W, et al. Network defense strategy selection based on best-response dynamic evolutionary game model[C]//Proceedings of 2017 IEEE 2nd Advanced Information Technology, Electronic and Automation Control Conference. Piscataway: IEEE Press, 2017: 2611-2615.

[69] SHI L Y, WANG X R, HOU H W. Research on optimization of array honeypot defense strategies based on evolutionary game theory[J]. Mathematics, 2021, 9(8): 805.

[70] 张恒巍, 黄健明. 基于Markov演化博弈的网络防御策略选取方法[J]. 电子学报, 2018, 46(6): 1503-1509.

ZHANG H W, HUANG J M. Network defense strategy selection method based on Markov evolutionary game[J]. Acta Electronica Sinica, 2018, 46(6): 1503-1509.

[71] HU H, LIU Y L, ZHANG H Q, et al. Optimal network defense strategy selection based on incomplete information evolutionary game[J]. IEEE Access, 2018, 6: 29806-29821.

[72] LIU X H, ZHANG H W, ZHANG Y C, et al. Optimal network defense strategy selection method based on evolutionary network game[J]. Security and Communication Networks, 2020, 2020: 5381495.

[73] 张恒巍, 李涛, 黄世锐. 基于攻防微分博弈的网络安全防御决策方法[J]. 电子学报, 2018, 46(6): 1428-1435.

ZHANG H W, LI T, HUANG S R. Network defense decision-making method based on attack-defense differential game[J]. Acta Electronica Sinica, 2018, 46(6): 1428-1435.

[74] 张恒巍, 黄世锐. Markov微分博弈模型及其在网络安全中的应用[J]. 电子学报, 2019, 47(3): 606-612. ZHANG H W, HUANG S R. Markov differential game model and its application in network security[J]. Acta Electronica Sinica, 2019, 47(3): 606-612.

[75] HUANG S R, ZHANG H W, WANG J D, et al. Network defense decision-making method based on stochastic differential game model[C]//Cloud Computing and Security, 2018: 504-516.

[76] 孙岩, 姬伟峰, 翁江, 等. 基于微分博弈的移动目标防御最优策略[J]. 计算机研究与发展, 2021, 58(8): 1789-1800.

SUN Y, JI W F, WENG J, et al. Optimal strategy of moving target defense based on differential game[J]. Journal of Computer Research and Development, 2021, 58(8): 1789-1800.

[77] DIJK M, JUELS A, OPREA A, et al. FlipIt: the game of “stealthy takeover”[J]. Journal of Cryptology, 2013, 26(4): 655-713.

[78] 丁绍虎, 齐宁, 郭义伟. 基于M-FlipIt博弈模型的拟态防御策略评估[J]. 通信学报, 2020, 41(7): 186-194.

DING S H, QI N, GUO Y W. Evaluation of mimic defense strategy based on M-FlipIt game model[J]. Journal on Communications, 2020, 41(7): 186-194.

[79] 丁绍虎. 信息通信网络中拟态防御机理与关键技术研究[D]. 郑州: 信息工程大学, 2020.

DING S H. Research on mimic defense mechanism and key technologies in information communication networks[D]. Zhengzhou: Information Engineering University, 2020.

[80] LASZKA A, HORVATH G, FELEGYHAZI M, et al. FlipThem: modeling targeted attacks with FlipIt for multiple resources[C]// Decision and Game Theory for Security, 2014: 175-194.

[81] 谭晶磊, 张恒巍, 张红旗, 等. 基于Markov时间博弈的移动目标防御最优策略选取方法[J]. 通信学报, 2020, 41(1): 42-52.

TAN J L, ZHANG H W, ZHANG H Q, et al. Optimal strategy selection approach of moving target defense based on Markov time game[J]. Journal on Communications, 2020, 41(1): 42-52.

[82] TAN J L, ZHANG H W, ZHANG H Q, et al. Optimal timing selection approach to moving target defense: a FlipIt attack-defense game model[J]. Security and Communication Networks, 2020, 2020: 3151495.

[83] MIURA H, KIMURA T, HIRATA K. Modeling of malware diffusion with the FLIPIT game[C]//Proceedings of 2020 IEEE International Conference on Consumer Electronics. 2020: 1-2.

[84] MERLEVEDE J, JOHNSON B, GROSSKLAGS J, et al. Exponential discounting in security games of timing[J]. Journal of Cybersecurity, 2021, 7(1)].

[85] PAWLICK J, ZHU Q Y. Strategic trust in cloud-enabled cyber-physical systems with an application to glucose control[J]. IEEE Transactions on Information Forensics and Security, 2017, 12(12): 2906-2919.

[86] LYE K W, WING J M. Game strategies in network security[J]. International Journal of Information Security, 2005, 4(1/2): 71-86.

[87] 王元卓, 林闯, 程学旗, 等. 基于随机博弈模型的网络攻防量化分析方法[J]. 计算机学报, 2010, 33(9): 1748-1762.

WANG Y Z, LIN C, CHENG X Q, et al. Analysis for network attack-defense based on stochastic game model[J]. Chinese Journal of Computers, 2010, 33(9): 1748-1762.

[88] WANG C L, MIAO Q, DAI Y Q. Network survivability analysis based on stochastic game model[C]//Proceedings of 2012 Fourth International Conference on Multimedia Information Networking and Security. Piscataway: IEEE Press, 2012: 99-104.

[89] 张红旗, 杨峻楠, 张传富. 基于不完全信息随机博弈与Q-learning的防御决策方法[J]. 通信学报, 2018, 39(8): 56-68.

ZHANG H Q, YANG J N, ZHANG C F. Defense decision-making method based on incomplete information stochastic game and Q-learning[J]. Journal on Communications, 2018, 39(8): 56-68.

[90] 杨峻楠, 张红旗, 张传富. 基于不完全信息随机博弈的防御决策方法[J]. 网络与信息安全学报, 2018, 4(8): 12-20. YANG J N, ZHANG H Q, ZHANG C F. Defense decision-making method based on incomplete information stochastic game[J]. Chinese Journal of Network and Information Security, 2018, 4(8): 12-20.

[91] 杨峻楠, 张红旗, 张传富. 基于随机博弈与改进WoLF-PHC的网络防御决策方法[J]. 计算机研究与发展, 2019, 56(5): 942-954.

YANG J N, ZHANG H Q, ZHANG C F. Network defense decision-making method based on stochastic game and improved WoLF-PHC[J]. Journal of Computer Research and Development, 2019, 56(5): 942-954.

Research review of network defense decision-making methods based on attack and defense game

LIU Xiaohu, ZHANG Hengwei, MA Junqiang, ZHANG Yuchen, TAN Jinglei

Information Engineering University, Zhengzhou 450001, China

Game theory studies the optimal decision-making problem under the condition of conflict confrontation. It is one of the basic theories of cyberspace security, and can provide a theoretical basis for solving the problem of network defense decision-making. The six game characteristics of network attack and defense were defined, such as goal opposition, strategy dependence, non-cooperative relationship, incomplete information, dynamic evolution and interest drive. Based on the hypothesis of rational player and limited resources, a 5-tuple network attack and defense game model was formally defined by using player, attack and defense strategy set, attack and defense action set, attack and defense information set and attack and defense income. The existing conditions of game equilibrium were analyzed, and the general process of network defense decision-making based on attack and defense game model was summarized. The applicable scenarios of network defense decision-making methods based on eight different types of game models were analyzed, such as complete information static game, complete information dynamic game, incomplete information static game, incomplete information dynamic game, evolutionary game, differential game, time game and random game, and summarizes their research ideas. The advantages and disadvantages of network defense decision-making methods based on different types of game models were given. The development process of network defense decision-making method based on attack defense game was summarized, and the advantages and characteristics of defense decision-making method was explained. It were pointed out that there were three problems in the research process, such as the relationship between the number of factors considered in game modeling and the complexity of the model, the dependence of game reasoning on information and data, and the generalization and migration of game model. It also looked forward to the next research direction from the description mechanism of normative strategy, the calculation method of optimizing revenue and the integration with other network security technologies. And the problems that should be solved were explained.

network defense, decision-making methods, attack and defense game,game characteristic

The National Key R&D Program of China (2017YFB0801900), Henan Science and Technology (222102210017)

刘小虎, 张恒巍, 马军强, 等. 基于攻防博弈的网络防御决策方法研究综述[J]. 网络与信息安全学报, 2022, 8(1): 1-14.

TP393

A

10.11959/j.issn.2096−109x.2021089

刘小虎（1989−），男，河南太康人，博士，信息工程大学副教授，主要研究方向为网络攻防博弈。

张恒巍（1977−），男，河南洛阳人，信息工程大学副教授，主要研究方向为网络安全风险评估、网络攻防博弈。

马军强（1975−），男，陕西大荔人，信息工程大学副教授，主要研究方向为指挥与管理。

张玉臣（1977−），男，河南新郑人，信息工程大学教授、博士生导师，主要研究方向为保密管理。

谭晶磊（1994−），男，山东章丘人，信息工程大学博士生，主要研究方向为移动目标防御。

2021−01−18；

2021−03−15

张恒巍，zhw11qd@163.com

国家重点研发计划（2017YFB0801900）；河南省科技攻关（222102210017）

Format: LIU X H, ZHANG H W, MA J Q, et al. Research review of network defense decision-making methods based on attack and defense game[J]. Chinese Journal of Network and Information Security, 2022, 8(1): 1-14.