高中物理碰撞及“类完全非弹性碰撞”问题的巧析
陈达超 樊佳欢
(江西师范大学物理与通信电子学院,江西 南昌 330022)
1 对于碰撞问题的理解
1.1 碰撞分为弹性碰撞、非完全弹性碰撞和完全非弹性碰撞
(1)弹性碰撞:碰撞后的两个物体都快速地恢复了原来的形状,只有能量的转移而没有能量的转化,此过程中机械能是守恒的,动量也守恒。
(2)非完全弹性碰撞:能量损失一小部分,机械能不守恒,但动量还是守恒的,两个物体的形状不能完全恢复,有部分能量转化为热能了。
(3)完全非弹性碰撞,两个物体相碰后不分开,连在一起了,动能损失最大,机械能不守恒,但动量还是守恒的。碰撞发生的过程伴随着声、光、热等的产生,系统总机械能因此而损失。
1.2 教学中遇到的问题
(1)教学过程中,学生往往不能很好地理解什么时候是动量守恒,什么时候是机械能守恒。
(2)由于弹性碰撞、非完全弹性碰撞和完全非弹性碰撞过程中的现象不明显,会对学生的理解造成极大的困难。
(3)教师在平时讲授碰撞问题的过程中倾向于用数学化的推导来得出碰撞的结论而忽视了碰撞中的物理过程,从而使得学生难以从物理的角度去理解碰撞过程中的物理现象,导致学生对于碰撞问题的理解模糊不清,甚至产生偏差。
1.3 对于碰撞问题的深入理解
(1)针对学生对于碰撞过程中遇到的理解困难问题,教师在教学碰撞问题的时候可以采用下类装置来便于学生理解碰撞中的物理过程。如图1所示,在碰撞的两个小球之间安装一个弹簧,当A球开始接触到弹簧,并且开始挤压弹簧直到A、B两球达到共速的时候,可以清晰地观察到A、B两球中间的弹簧被挤压而缩短,这时候说明弹簧具有一定的弹性势能。同时还能知道,只有当A、B两球共速的时候弹簧的缩短量是最大的。因此A、B构成的系统的机械能不守恒,并且由于能量守恒可以知道碰撞前系统的机械能大于碰撞后的机械能。由此可以得出当A碰撞B达到共速的时候,机械能是不守恒的,并且机械能的损失是最大的,即完全非弹性碰撞。这样的教授过程可以使得学生更好地观察到碰撞过程中的物理过程,而不是让学生的注意力完全集中在数学计算上。
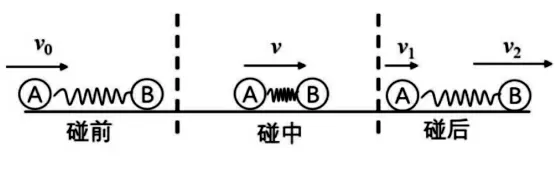
图1 小球碰撞模型
(2)同时可以知道当A球和B球分开的时候,弹簧是处于原长的状态,所以弹簧是不具备弹性势能。由此可以知道这种碰撞是没有机械能损失的,即完全弹性碰撞。
(3)弹簧有挤压,但是没有挤压到最短的位置,这时候弹簧具有弹性势能,但具有弹性势能并非是最大状态,即非完全弹性碰撞[1]。
通过上述的方法,可以把碰撞过程中的物理过程放大,使得学生理解碰撞过程中的物理过程,明白原来机械能的损失是由于小球碰撞过程中的小球形变产生的。有的小球在碰撞过程中产生的形变在碰撞结束后可以恢复原来的形状,这就相当于图1中的弹簧可以恢复原长,不产生机械能的损失,属于弹性碰撞。有的小球在碰撞过程中产生的形变在碰撞结束后不可以恢复原来的形状,这就相当于图1中的弹簧压缩到最短的情况,产生机械能的损失最大,属于完全非弹性碰撞。有的小球介于这两者之间,属于非完全弹性碰撞。
1.4 完全非弹性碰撞的深入理解
通过上面的解析,可以明白完全非弹性碰撞是有机械能损失的,且机械能的损失是最大的。在此基础上结合高中物理碰撞类题目可以发现,高中物理题目中完全非弹性碰撞的能量损失只涉及热能和形变所产生的能量的损失。因此在本文中不讨论由于光、声等因素导致完全非弹性碰撞中机械能的损失。
高中题目中由于物体形变及发热引起的系统机械能损失模型如下:模型1和模型2就是经典的完全非弹性碰撞的物理模型。在模型1中机械能的损失是由于球体发生形变并且不能恢复而产生的,而模型2中的机械能损失是由于子弹在物块中摩擦生热而导致的。结合上面图1的模型,都可以把模型1中由于球体形变而损失的这部分机械能和模型2中由于摩擦而损失的这部分机械能理解为储存在了图1模型中的弹簧内,且这部分储存的能量不能再次释放出来。
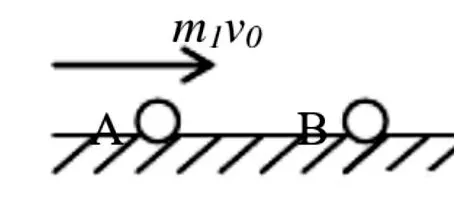
模型1:A、B两球质量都为m1,碰撞前A球以v0速度碰撞B球,碰撞后A、B两球都以v的速度共同向右运动。
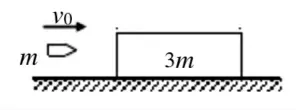
模型2:子弹质量为m,初速为v0,射向一质量为3 m的物块,之后它们以速度v共同向右运动。
1.5 “类完全非弹性碰撞”的深入理解
类完全非弹性碰撞是指具有完全非弹性碰撞的特点,即碰撞后物体达到共速,但在碰撞的整个过程中,系统的机械能却是守恒的。因此本文中将这类题型定义为“类完全非弹性碰撞”问题。其典型模型就如图2所示:小球A与小球B之间存在一个弹簧,小球A以初速度v0碰撞静止的小球B,当A、B两球达到共速的时候,A、B小球构成的系统损失的动能转化为弹簧的弹性势能,系统过程的机械能不变,这样的模型我们将其定义为“类完全非弹性碰撞”。
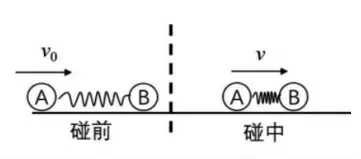
图2 类完全非弹性碰撞模型
2 完全弹性碰撞及“类完全非弹性碰撞”问题的巧析
高中阶段有大量的完全非弹性碰撞及“类完全非弹性碰撞”的题目,许多学生对于这类题目难以下手,因此下文中针对这两类题型进行巧析,希望对读者有所启示。
2.1 完全非弹性碰撞问题的巧析
通过上文中对完全非弹性碰撞的深入理解,笔者知道了在完全非弹性碰撞的题目中可以把系统损失的那部分机械能认为是储存在图1模型中的弹簧中,并且这部分能量是取不出来的。并且结合高中物理完全非弹性碰撞的题目,可以发现,高中物理完全非弹性碰撞的题目只涉及碰撞过程中由于发热而导致机械能损失的计算。这就意味着学生在解题的时候可以把这份损失的能量和题目所要求的量建立起联系来,从而解出答案,使得解题过程和思维难度都有所降低[2]。例如,在例题1中就可以用该方法进行求解。
例题1:如图3所示,一质量为m=1 kg的物块A放在一质量为M=2 kg的凹槽B物体上,A、B之间的摩擦系数为0.2。当物块A以初速v0=6 m/s向右运动时,A物块在凹槽B中与凹槽B发生反复的碰撞最终与凹槽B一起达到共速,求此过程中A物块运动的路程。
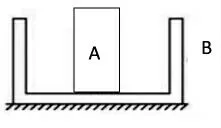
图3 完全非弹性碰撞例题
解析:由于A物块一开始有速度,而凹槽B没有速度,最终两物体一起共速向右运动,且A、B之间存在摩擦力,由此可以知道A、B过程的系统符合完全非弹性碰撞的模型。并且可以通过动量守恒定律算出其碰撞前后的速度,进而算出系统碰撞前后机械能的损失量。有了机械能的损失量,再把这一能量和题目所求的物理量联系起来,最终得出答案。
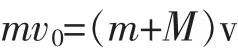
得v=2m/s,
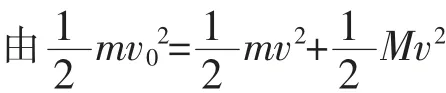
得机械能的损失量ΔE=12J,
A、B之间的摩擦力f=mgμ=2N
所以s=ΔE/f=6 m
2.2 “类完全非弹性碰撞”问题的巧析
通过对上文中的完全非弹性碰撞的深入理解我们知道了,所有的完全非弹性碰撞都可以把它们损失的那部分能量看成是存储在了图1模型中的弹簧里,只是在完全非弹性碰撞中不能把储存在弹簧里的这部分能量给取出来。但在某些“类完全非弹性碰撞”的题目中这部分能量就能再次释放出来,且在整个过程中机械能是守恒的,所以可以把这类题目看成是完全非弹性碰撞进行求解,因此本文把这类题目称为“类完全非弹性碰撞”题目。例如,例题2就是一种“类完全非弹性碰撞”的题目。
例题2:如图4所示,小球A和1 4圆弧面的实验小车,原来静止在光滑的水平地面上,一个质量m=1 kg可视为质点的小球以v0=10m/s的水平速度冲上小车,小车质量M=4 kg,其左端水平且距地面高度h=0.2 m,g取10 m/s2,求小球冲上小车后能上升的最大高度?
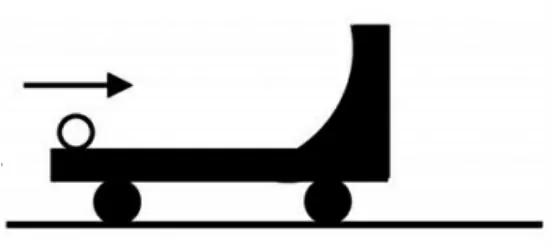
图4 类完全非弹性碰撞例题
在该题中,没有涉及弹性形变和摩擦生热从而导致机械能损失的情况,因此把小球和小车看成一个系统,则系统的机械能是守恒的。但是由于小球滑上小车并在小车右端开始向上运动,当小球到达最高点时,小球与小车以共同的速度向右运动,因此可以把这个问题看成是“类完全非弹性碰撞”的问题来解决[3]。
解析:小球A运动到最高点过程中,A和B在水平方向上合外力为零,在水平方向上系统动量守恒。在最高点处,小球A和圆弧轨道B共速,故可知mv0=(m+M)v,此时v为小球到达最高点时小球和车的速度。把小球和车看成一个系统,则系统损失的动能Δ全部转换为小球A的重力势能。由此我们可以得到h=1.47m。
在该题目中,虽然系统的机械能没有损失,但是依然可以近似地认为小球和小车发生的是完全非弹性碰撞,且把系统中损失的动能储存在了小球的重力势能中。结合图1的模型就可以理解为,小球碰撞小车最终达到共速,而小球的重力势能就相当于模型中的弹性势能。
通过上面的分析可以清晰地知道在“类完全非弹性碰撞”的题目中,虽然没有涉及系统机械能的损失,但是依然可以近似地认为系统是在做完全非弹性碰撞,且系统损失的动能以另外别的能量形式给储存起来。
3 结语
本文从对碰撞问题的分析理解上努力让学生明白什么是完全弹性碰撞、非完全弹性碰撞及完全非弹性碰撞,并从物理学的角度解释了完全非弹性碰撞机械能损失的原因。同时介绍了高中物理中常见的完全非弹性碰撞及“类完全非弹性碰撞”的模型,并在此基础上结合高中物理常见的题目巧析这两类题型,希望能够给予广大的教师或学生以启迪。

